Динамика точки. Дифференциальные уравнения движения материальной точки

1. Теоретическая механика

Динамика точки

2. 2.1. Дифференциальные уравнения движения материальной точки

Уравнения в декартовых координатах:
x=f1(t), y=f2(t), z=f3(t).
d 2x
m 2 Fkx
dt
m x Fkx
d2y
m 2 Fky
dt
или
d 2z
m 2 Fkz
dt
m y Fky
m z Fkz
В общем случае, т.к. действующие силы могут
зависеть от времени t, положения точки x,y,z, и от
скорости, то правая часть уравнений может быть
функцией всех переменных t , x, y , z , x , y , z
2

3.

2.2. Решение первой задачи динамики
(определение сил по заданному движению).
d r
m 2 F
dt
2
d 2x
m 2 Fkx
dt
d2y
m 2 Fky
dt
d 2z
m 2 Fkz
dt
3

4.

2.2. Решение первой задачи динамики
(определение сил по заданному движению).
m
d
F
dt
2
m Fn
0 Fb
1. Движение по прямой
2. Движение по дуге
3. Движение кривошипа
4

5. Движение по прямой

5

6.

2.3. Решение основной (второй) задачи
динамики при прямолинейном движении точки
(определение закона движения по заданным
силам).
Дифференциальное уравнение прямолинейного движения
точки
d 2x
или
m x Fkx
m 2 Fkx
dt
Иногда его удобнее заменить двумя уравнениями,
содержащими первые производные
d x
dx
m
Fkx , x.
dt
dt
d x
dx
d x d x dx d x
m
F
,
или
x
x
kx
x , т.к.
dx
dt
dt
dx dt
dx

7.

2.3. Решение основной (второй) задачи
динамики при прямолинейном движении точки
(определение сил по заданному движению).
В общем случае имеем дифференциальное
уравнение 2-го порядка
m x F t , x, x
Интегрируя это уравнение дважды, можем получить
уравнение движения материальной точки.
После интегрирования общее решение имеет вид
x f t , C1 , C2
По начальным условиям определяются постоянные
интегрирования С1 и С2.
Частное решение
x f t , x 0 , 0
7

8. Решение задач динамики точки путем интегрирования соответствующих дифференциальных уравнений движения сводится к следующим

операциям:
1. Составление дифференциального уравнения
движения:
Выбрать оси координат и начало отсчета
Изобразить точку и указать все действующие
силы
Подсчитать сумму проекций всех сил на
координатную ось
2. Интегрирование дифференциального уравнения
движения.
3. Определение постоянных интегрирования.
4. Нахождение искомых величин.
8

9. Материальная точка с массой m движется под действием постоянной по модулю и направлению силы Q. Найти закон движения точки при

начальных условиях: t=0, x=x0, x= 0.
d x
m
Q
dt
x Q / m t C1
dx
Q / m t C1
dt
x Q / 2m t 2 C1t C2
Учитывая начальные условия, получим:
0 C1 , x0 C2 . Тогда уравнение движения:
x x0 0t Q / 2m t 2
9

10.

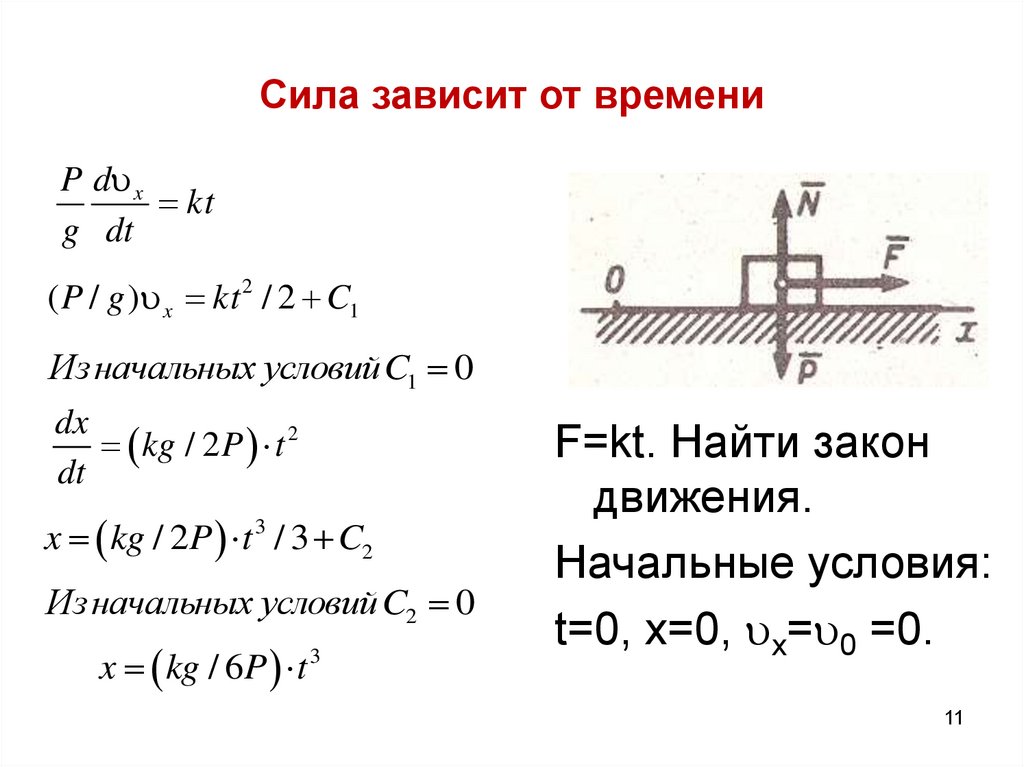
10

11. Сила зависит от времени

P d x
kt
g dt
( P / g ) x kt 2 / 2 C1
Из начальных условий C1 0
dx
kg / 2 P t 2
dt
x kg / 2P t 3 / 3 C2
Из начальных условий C2 0
x kg / 6P t 3
F=kt. Найти закон
движения.
Начальные условия:
t=0, x=0, x= 0 =0.
11

12.

12

13. Сила зависит от скорости

Начальные условия:t=0, x=0,
x=0,5 м/с.
R= x.
d
m
.
dt
d
dt
или
ln
ln
t
0
m 0
m
0
t
t m / ln 0 / 3 с.
d
m
.
dx
d
dx
или
x
0
m0
m
0
x m / 0 1,1 м.
x
При 0, x 2,2 м.
Лодка массой m=40 кг, 0=0,5
м/с. R= . Где =9,1 кг/с.
Определить время за
которое скорость лодки
уменьшится вдвое и какой
путь она пройдет за это
время. Также определить
путь до полной остановки.
13

14.

14

15. Сила зависит от координаты

Начальные условия:t=0, x=a, x=0.
F F cos mg / R r cos mg / R x
kx
Введем обозначение g/R=k2, тогда
2
2 2
d x
2
/
2
k
x / 2 C1
x
k x
x
dx
Из начальных условий находим:
C1 k 2a 2 / 2 тогда x k a 2 x 2 . Радиус Земли R=6370 км.
dx
dx
k a 2 x 2 . kdt
.
2
2
dt
a x
kt arccos x / a C2 .
Определить время движения по АВ.
F=(mg/R)r,
где r=МС – расстояние от точки М
до центра Земли.
Из начальных условий находим, что С2=0.
x a cos kt
При x -a получим cos(kt) -1, t /k g/R 42 мин 11с.
15

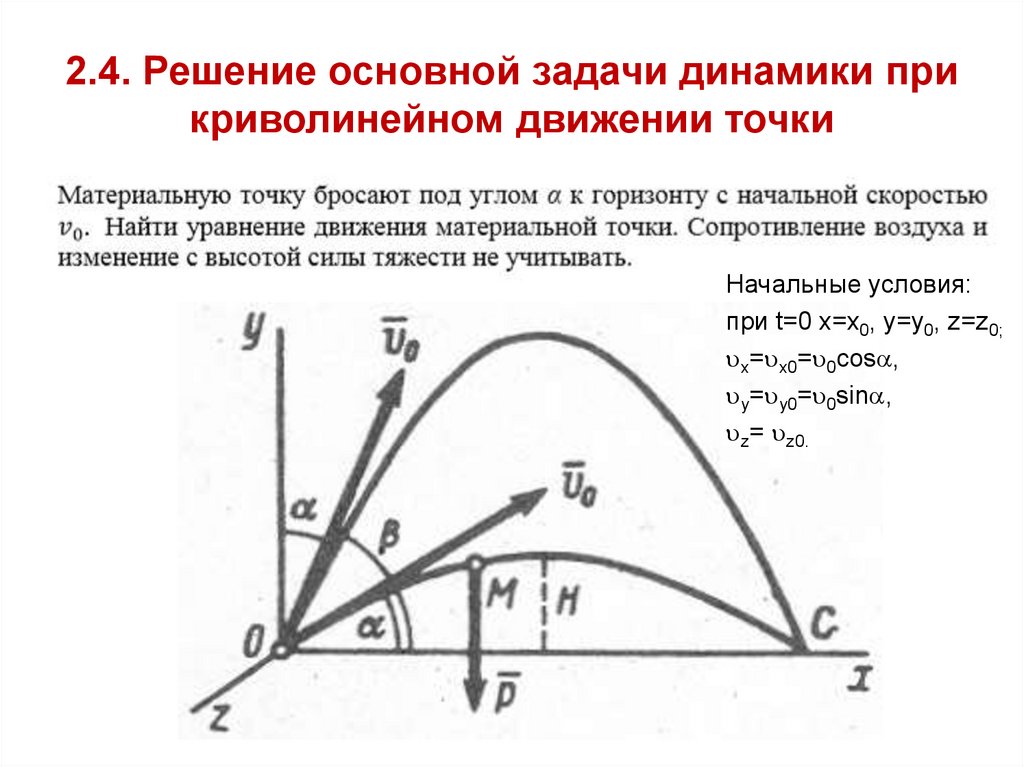
16. 2.4. Решение основной задачи динамики при криволинейном движении точки

Начальные условия:
при t=0 x=x0, y=y0, z=z0;
x= x0= 0cos ,
y= y0= 0sin ,
z= z0.
16

17.

17

18.

18

19. Решение основной задачи динамики при криволинейном движении точки

Проекция силы тяжести на оси:
Px=0, Py=-P=-mg, Pz=0;
Диф. ур-ния после сокращения на m:
d y
d x
d
0,
g, z 0
dt
dt
dt
Начальные условия:
при t=0 x=x0, y=y0, z=z0;
x= x0= 0cos ,
y= y0= 0sin ,
z= z0.
После интегрирования:
x=С1, y= -gt+C2, z=C3.
Согласно начальным условиям:
С1= 0cos , С2= 0sin , С3=0.
Тогда
dx
dy
dz
0 cos ,
0 sin gt , 0
dt
dt
dt
После интегрирования:
X= 0tcos +C4, y= 0tsin -gt2/2+C5, z=C6.
C4=C5=C6=0
19

20. Решение основной задачи динамики при криволинейном движении точки

Окончательные уравнения
движения точки М:
x= 0tcos , y= 0tsin -gt2/2, z=0.
1. Траектория точки. Исключим t:
2. Горизонтальная дальность:
3. Высота траектории. Если
учесть что
x X/2 / g sin cos
2
0
то высота определяется как:
4. Время полета определяется из
уравнения X= 0Tcos :
gx 2
y xtg 2
2 0 cos 2
x1 0, x2 2 02 cos 2 tg / g
X x2 02 / g sin 2
H 02 / 2 g sin 2
T 2 0 / g sin
20