Динамика материальной точки, теория моментов

1. Лекция №5

2.

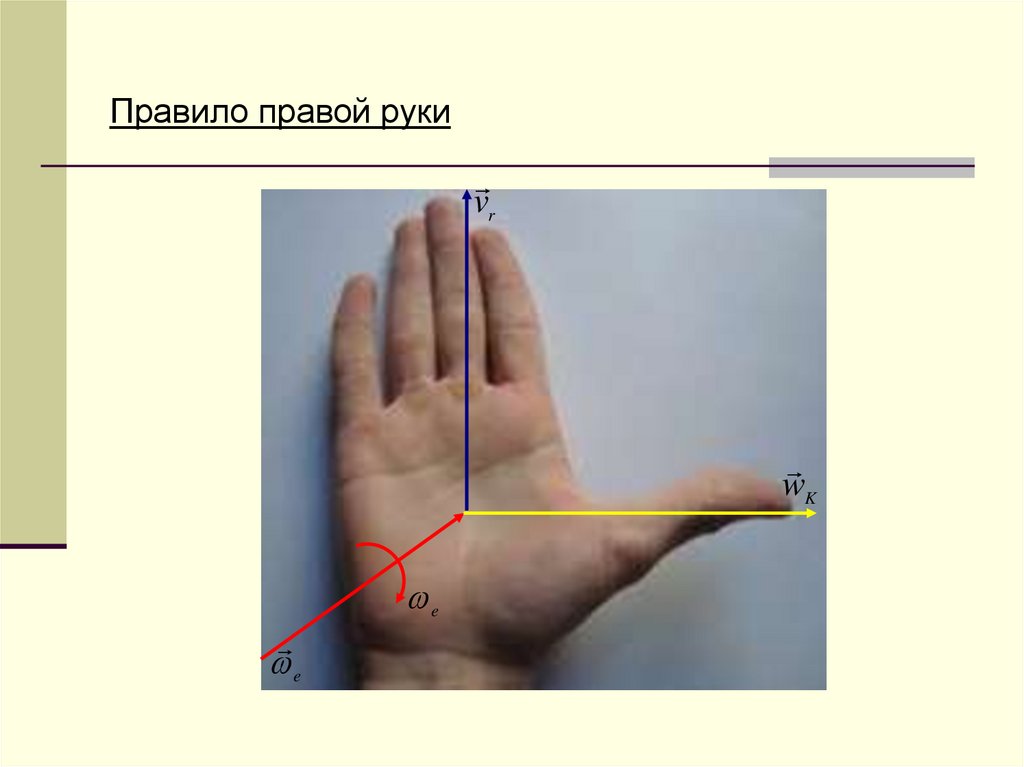
Правило правой руки
vr
wK
e
e

3.

Частные случаи:
1.
Если переносное движение является
поступательным, то e 0 и wK 0 .
2. Если e vr , то wK 0 .

4. Кинетика

Изучает движение тел с учетом причин,
вызвавших это движение

5. 1. Динамика материальной точки

1.1. Основные аксиомы динамики.
1. Аксиома инерции.
Существуют такие инерциальные системы отсчета, в
которых если на МТ не действует никакой объект,
то она не изменяет своего кинематического
состояния.

6.

2. Основной закон динамики.
Ускорение любой свободной МТ прямо
пропорционально действующей силе и обратно
пропорциональна массе:
F
w
m

7.

3. Аксиома действия и противодействия.
Сила действия 1-ой МТ на вторую вызывает со
стороны 2-ой МТ противодействие, равное по
величине действию и обратно по направлению.

8.

4.
Аксиома независимости действия сил.
Результат действия некоторой системы сил на МТ
не зависит от порядка приложения сил в данную
материальную точку, т.е.
Fi
k
i 1
w
m

9.

5. Аксиома связи.
Определение. Связью называют тело,
ограничивающее свободу перемещения заданного
тела. Если на тело наложена связь, то оно
несвободно.
Любую связь можно отбросить, заменив ее действие
силой, которую называют реакцией связи.

10.

Следствие: ускорение несвободной
материальной точки прямо
пропорционально действующим силам и
силам и силам реакции связей

11. 1.2. Дифференциальные уравнения движения МТ.

Для вывода дифференциальных уравнений
воспользуемся
основным законом
F .
динамики: w
m
Векторное движение МТ.
2
dv d r
2
r r (t ) , тогда w
dt dt
2
dv F
d r F
и
2
dt m
dt
m
1.

12.

2. Координатное движение МТ.
dv x d 2 x
wx dt dt 2 ,
x x (t ),
dv y d 2 y
2,
y y (t ), wy
dt
dt
z z (t ).
dv z d 2 z
wz dt dt 2 .
2
d
x Fx
dv x Fx
,
,
2
dt
m
Тогда dt
и
m
2
d y Fy
dv y Fy
,
2 ,
m
m
dt
dt
2
d
z Fz
dv
F
z
z
.
.
2
dt m
m
dt

13.

3. Естественное движение МТ.
2
dv d s
s s(t ) w 2
dt dt
dv F
Тогда dt m ,
2
v Fn
m
и
1 ds
и wn
dt
v2
d 2 s F
dt 2 m ,
2
1
ds
Fn
dt
m
2

14.

Все задачи на динамику МТ делятся на два типа:
Первая задача динамики (прямая). По заданной
массе и закону движения определить силу,
действующую на МТ.
Вторая задача динамики (обратная). По заданной
массе и силе определить кинематические
характеристики, если заданы начальные условия.

15. 1.3. Дифференциальное уравнение относительного движения

Рассмотрим сложное движение МТ. Для нее
справедлив основной закон динамики:
F
w
, где абсолютное ускорение: w wr we wK
m
Выразим относительное ускорение:
ин ин
F
F Fe FK
wr we wK wr
m
m
ин
ин
Fe mwe
FK mwK
и
, где

16.

Динамическая теорема Кориолиса:
В относительном движении материальная точка
движется под действием трех сил: заданной силы,
переносной силы инерции, силы инерции
Кориолиса.
Определение. Весом тела P называют величину
нормальной реакции поверхности на это тело.
Явлением невесомости называют состояние, при
котором вес тела равен нулю.

17. 1.4. Движение точки по гладкой и шероховатой поверхностям

Определение. Поверхность называется гладкой, если
реакция поверхности
направлена по нормали к этой
поверхности: R N
R N
w

18.

Определение. Поверхность называется
шероховатой, если реакция поверхности
направлена не по нормали к этой поверхности:
R N Fтр
R
Fтр
N
w
Fтр
Fтр tg N f N
tg
N

19. 2. Теория моментов

2.1. Алгебраический момент силы относительно точки.
Определение. Алгебраическим моментом силы
относительно точки называется произведение
величины силы на плечо, взятое со знаком «+», если
сила поворачивает плечо против часовой стрелки, и
со знаком «-» - наоборот:
M O ( F ) F h , где плечо – кратчайшее
расстояние от моментной точки до линии действия
силы

20.

ЛД (F )
А
F
В
h
О
OAB - силовой треугольник, тогда
M O ( F ) F h 2 S OAB

21.

Свойства:
1. От переноса силы вдоль линии действия
алгебраический момент не меняется.
2. Если моментная точка принадлежит линии
действия, то алгебраический момент равен 0.
3. M ( F ) M. ( F )
O
O
4. M ( F F ) M ( F ) M
. ( F )
O
1
2
O
1
O
2