Similar presentations:
Динамика материальной точки
1. ГЛАВА I. МЕХАНИКА §4. Динамика материальной точки
О. И. ЛубенченкоНИУ МЭИ
Кафедра физики им. В. А. Фабриканта
2020
2. §4. Динамика материальной точки
Динамика — раздел механики, изучающий влияние взаимодействия тел намеханическое движение.
I. Законы Ньютона
I закон Ньютона: существуют такие системы отсчёта, в которых
материальная точка сохраняет состояние покоя или равномерного
прямолинейного движения до тех пор, пока воздействие других объектов не
выведет её из этого состояния.
II закон Ньютона: ускорение материальной точки совпадает по
направлению с силой, с которой действуют на неё другие тела, и равно
отношению этой силы к массе точки:
a
F
m
a
F
m
III закон Ньютона: две материальные точки действуют друг на друга с
силами, равными по модулю, противоположными по направлению и
направленными вдоль прямой, соединяющей эти точки:
F 12 F 21
F 21
1
2
F 12
2
3. §4. Динамика материальной точки
II. Инерциальные системы отсчёта. ИнертностьИнерциальная система отсчёта (ИСО) — система отсчёта,
относительно которой материальная точка, не испытывающая внешних
воздействий, движется равномерно и прямолинейно.
ИСО
гелиоцентрическая
тело отсчёта — Солнце
лабораторная
тело отсчёта — лаборатория
(земля)
Все тела обладают инертностью — свойством сохранять состояние покоя
или равномерного прямолинейного движения в отсутствие внешних
воздействий.
Масса — скалярная ФВ — характеристика тела, являющаяся мерой его
инертности;
m кг
3
4. §4. Динамика материальной точки
4III. Сила
Сила — векторная ФВ — мера воздействия на данное тело другого ФО. Каждая
сила описывает действие какого-либо ФО;
F Н ньютон
Линия действия силы — прямая, вдоль которой направлена сила.
Силовая линия — кривая, касательные к которой в каждой её точке
совпадают по направлению с силой.
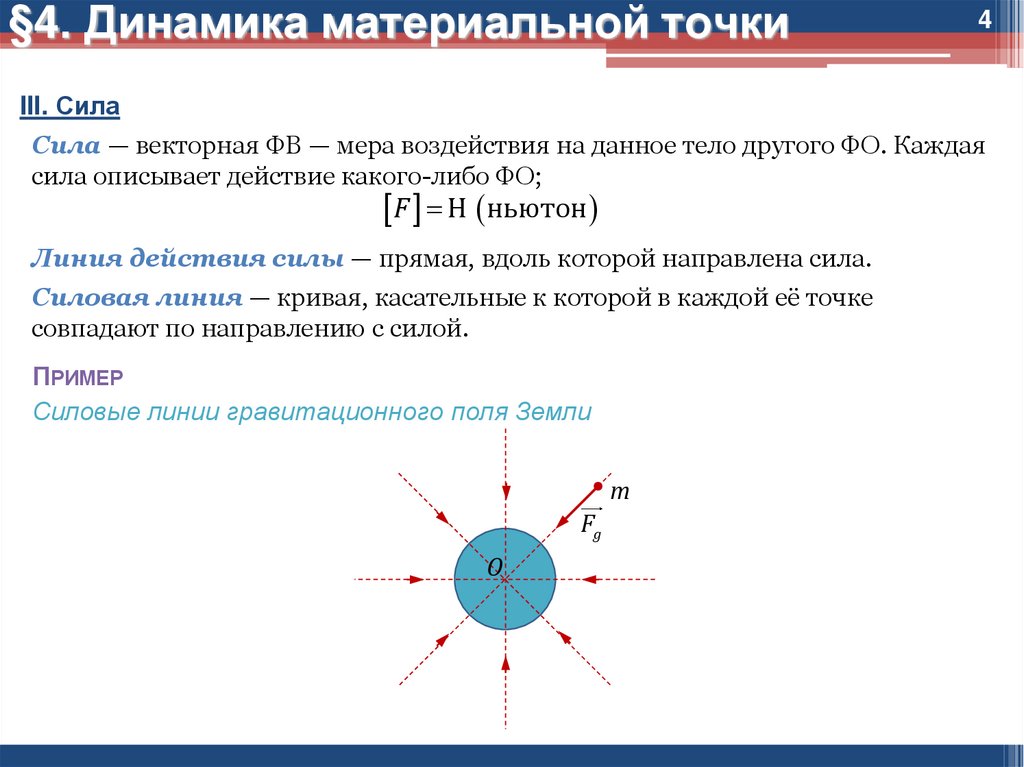
ПРИМЕР
Силовые линии гравитационного поля Земли
m
Fg
O
5. §4. Динамика материальной точки
Главный вектор — векторная сумма всех сил, описывающих действие наданное тело других ФО:
n
F Fi
i 1
n — число воздействующих объектов
Принцип независимости действия сил: если на материальную точку
одновременно действует n ФО, то ускорение этой точки
n
a
d2 r
a 2
dt
F
i 1
i
m
d2 r
m 2 F — дифференциальное уравнение
dt
движения материальной точки
F — главный вектор сил, с которыми другие ФО действуют на данную МТ
5
6. §4. Динамика материальной точки
d2xm dt 2 Fx
2
d y
m 2 F y
dt
d2z
m 2 Fz
dt
IV. Центр масс механической системы
Внешние силы — силы, описывающие действие ФО, не входящих в данную
e
механическую систему, на тела, входящие в неё. F
Внутренние силы — силы, описывающие взаимодействие тел, входящих в
i
данную механическую систему. F
III закон Ньютона
F
i
0
7. §4. Динамика материальной точки
Рассмотрим механическую систему из N материальных точек.Центр масс механической системы — точка,
m1
C
для которой
ρi
m2
rC
N
mi
m ρ
mN
i
i 1
i
m r r 0
N
0 или
i
i 1
i
ri
O
N
N
m
r
m
i i
i rC
i 1
i 1
N
rC
m r
i 1
N
xC
m x
i
i 1
M
N
i i
M mi
M
i 1
N
i
yC
m y
i 1
i
M
N
i
zC
m z
i i
i 1
M
C
8. §4. Динамика материальной точки
ПРИМЕРНахождение центра масс системы двух МТ
Две МТ массами m1 и m2 находятся на расстоянии l друг от друга. Где
находится ЦМ системы?
m1
O
C
ρ1 xС
ρ2
m2
x
l
m1 x1 m2 x2
m2l
xC
m1 m2
m1 m2
Теорема о движении центра масс: центр масс механической системы
движется как материальная точка с массой, равной массе системы, к которой
приложена сила, равная равнодействующей внешних сил, приложенных к
системе:
MaC F
e
Доказательство
Механическая система состоит из N МТ. Дифференциальное уравнение
движения i-ой МТ
N
e
i
d 2 ri
mi 2 Fi F ki
dt
k 1, k i
9. §4. Динамика материальной точки
id 2 ri N e N N
mi 2 Fi F ki
dt
i 1
i 1
i 1 k 1, k i
N
0
ri rC ρi
e
d 2 rC N
d 2 ρi
mi 2 mi 2 F
dt
dt
i 1
i 1
N
d 2 rC
dt 2
d 2 rC
aC
2
dt
e
d2 N
m
m
ρ
F
i
2 i i
dt
i 1
i 1
N
N
N
m M
i 1
m ρ
i
MaC F
i 1
e
i
i
0
10. §4. Динамика материальной точки
V. Некоторые силы1. Гравитационная сила
Сила, описывающая гравитационное воздействие МТ массой m1 на МТ
массы m2, находящуюся на расстоянии r от точки массой m1:
m1m2
r 12 — закон всемирного тяготения
3
r
m1
2
Н
м
G 6,67 10 11
— гравитационная постоянная
2
кг
F 12 G
F 12
r 12
ПРИМЕР
Сила тяжести — гравитационная сила вблизи поверхности Земли:
Fт mg
O R
r
M
Fg Fт
mM
M
r
F
G
m mg
т
m
3
2
R
R
M
м
g G 2 9,81 2 — ускорение свободного падения
R
с
ma mg
Fg Fт G
m2
11. §4. Динамика материальной точки
2. Сила упругостиУпругая деформация — деформация тела, которая полностью исчезает
после прекращения взаимодействия, являющегося её причиной. Воздействие
деформированного тела на тело, вызвавшее деформацию, описывается
силой упругости.
Линейная деформация подчиняется закону Гука: F упр kΔl
Δl — вектор деформации, k — коэффициент упругости (жёсткость)
Н
деформируемого тела
k м
F упр
k
0
m
Δl
T
m
m
N
Вес тела — сила, описывающая действие тела на опору или подвес.
P T
P N
12. §4. Динамика материальной точки
3. Сила сухого тренияСила трения — составляющая силы взаимодействия соприкасающихся тел,
параллельная поверхности их контакта. Наличие этой составляющей
обусловлено неупругими деформациями тел.
Закон сухого трения (закон Кулона): Fтр max μN
µ — коэффициент трения — безразмерная ФВ; зависит от материала и
состояния соприкасающихся поверхностей.
F тр
N
m
v
Fт
F
Fтр
µN
0
µN
F
VI. Кинематические связи
Кинематическая связь — ограничение, накладываемое на движение
тела.
13. §4. Динамика материальной точки
1. Координатная связьПРИМЕР
Тело скользит по горизонтальному прямому рельсу.
y, z 0
r xi
v
a
x
v v x i v y , vz 0
2. Нить
a ax i
a y , az 0
а) Невесомая нить
Рассмотрим участок натянутой нити 1-2. По условию невесомости масса
этого участка Δm = 0. Участки нити, находящиеся по обе стороны от данного
участка, действуют на него с силами T1 , T2 .
Δm = 0
По т. о движении ЦМ
2 T2
T1 1
Δma T1 T2
0
T2 T1
T1 T2
14. §4. Динамика материальной точки
б) Нерастяжимая нитьМодуль скорости всех точек натянутой нити одинаков: v const
Доказательство
Будем отсчитывать координаты точек нити по её длине от некоторой точки
(например, одного из концов нити). Рассмотрим участок нити 1-2. Координата
точки 1 равна l1, координата точки 2 соответственно равна l2 По условию
нерастяжимости длина этого участка должна оставаться постоянной:
v2
Δl = l2 – l1 = const.
2
dl1
dl2
v1
dt
v2
dt
v1
0
dl dl d l2 l1
v2 v1 2 1
0
dt dt
dt
Отсюда aτ 2 aτ 1
v2 v1
1
15. §4. Динамика материальной точки
VII. План решения задач по динамике1. Выбор объекта исследования и его модели: материальная точка, твёрдое
тело, механическая система (указать, какие тела в неё входят)
2. Выбор системы отсчёта (в большинстве случаев — лабораторная)
3. Рисунок (или несколько рисунков)
4. Определение воздействующих объектов. Расстановка обозначений на
рисунке: сил, ускорений и т. д.
5. Запись II закона Ньютона (теоремы о движении центра масс) в
векторной форме
6. Выбор системы координат (можно вводить разные системы координат
для разных тел)
7. Запись закона в проекциях на оси системы координат
8. Подсчёт числа уравнений и числа неизвестных. Запись дополнительных
уравнений (другие законы, уравнения связей и т. п.)
9. Решение полученной системы уравнений в общем виде
10. Анализ результата и проверка размерностей
11. Численный расчёт и оценка его результата
16. §4. Динамика материальной точки
VIII. Импульс. Другая форма II закона Ньютонаma F
dv
a
dt
F
d mv
dt
dv
m
F
dt
— II закон Ньютона в дифференциальной форме
Импульс материальной точки — векторная ФВ, характеризующая
инертность и движение тела (количество движения):
p mv
p
кг м
с
d mv Fdt Fdt — импульс силы
II закон Ньютона: изменение импульса МТ равно импульсу силы.
Импульс механической системы равен сумме импульсов тел (МТ),
входящих в эту систему:
P pi
17. §4. Динамика материальной точки
Импульс механической системы равен произведению массы системы наскорость её центра масс:
P M vC
Доказательство
P pi mi vi mi
d
P
dt
dri d
mi ri
dt dt
0
mi rC mi ρi mi
Т. о движении ЦМ: MaC F
e
e
Если система замкнута, то F 0 и
dP
0
dt
ri rC ρi
e
d vC
M
F
dt
drC
Mv
dt
d M vC
dt
F
e
e
dP
F
dt
P const — закон сохранения импульса механической
системы: импульс замкнутой системы остаётся
неизменным с течением времени.
















 physics
physics








