Similar presentations:
Степень с рациональным показателем
1. Степень с рациональным показателем.
из 29 слайдов, слайд №1
2.
УстноКорнем n-й степени из числа а называется такое число х,
которое после возведения в n-ю степень дает а.
Это определение можно записать так:
Например:
Арифметическим корнем n—ой степени из
неотрицательного числа a называется неотрицательное
число, n—ая степень которого равна a.
Показатель корня
n
a
Знак
Подкоренное
арифметического
выражение
корня (радикал) из 29 слайдов, слайд №
2
3.
из 29 слайдов, слайд №3
4.
УстноКорень нечетной степени из положительного числа
положителен, из отрицательного—отрицателен, т. е.
корень нечетной степени имеет тот же знак, что и
подкоренное число.
Корень четной степени из отрицательного числа не
существует
из 29 слайдов, слайд №
4
5.
Свойства арифметических корнейСвойства корней n—ой степени сходны со свойствами
квадратных корней
Но квадратные корни имели одинаковые показатели = 2,
поэтому чтобы действовать по аналогии с квадратными
корнями мы должны уравнивать показатели корней, т.е.
приводить корни к одинаковым степеням. Для этого
используется основное свойство корня:
Величина корня не изменится, если показатель степени
корня и показатель степени подкоренного выражения
умножить на одно и то же число, не равное нулю, т. е.
из 29 слайдов, слайд №
5
6.
Читая то же самое тождество справа налево, получим:показатель степени корня и подкоренного выражения можно
разделить на их общий делитель.
из 29 слайдов, слайд №
6
7.
Данное свойство используется для сравнения корнейПримеры: 1. Что больше: 4 3 3 или 8 3 7 ?
Приведем корни к одинаковым показателям. Для этого найдем
наименьшее из чисел, которое делится и на 4 и на 8. Это число 8.
4
3
3
4 2
3
3 2
3
8
8
6
2. Что больше:
6
3
6
33
8
или
3 , т.к.3 3
7
9
34
6
7
4
33 8 3 7
?
Приведем корни к одинаковым показателям. Для этого найдем
наименьшее из чисел, которое делится и на 6 и на 9 . Это число 18
6
33 6 3 33 3 18 39 ; 9 3 4 9 2 3 4 3 18 312 , т.к.39 312
18
3 9 18 312
6
33
9
из 29 слайдов, слайд №
34
7
8.
1. Что больше:2. Что больше:
8
13 3
или
4
13
из 29 слайдов, слайд №
?
8
9.
Проверьте себя:1) 8 133 4 13
2) 9 5 18 25
из 29 слайдов, слайд №
9
10.
n am
Пример:
n am
5
-это еще одно важное свойство корня,
которое нужно знать.
3
5
8 8 3
из 29 слайдов, слайд №
10
11.
Переход от корня к степениm 0, n 0
m
n
m
a an
Степень с дробным (положительным) показателем есть
корень, показатель степени которого равен знаменателю
дробного показателя, а подкоренное выражение
представляет собой степень того же основания с
показателем, равным числителю дробного показателя.
Будем рассматривать корень любой степени с a>0. Тогда извлечение корня из
чисел можно заменить действием возведения в степень.
из 29 слайдов, слайд №
11
12.
Примеры:3
1) 4 a 3 a 4 ;
7
4) 10 p 7 p 10 p 0,7 ;
2
3) 3 8 2 8 3 ;
1
2) 7 b 7 b1 b 7 ;
5
1
2
4
1
4
3
5
3
3
4
5) (a b) a b 4 a b 4 ; 6) x y
7) 4 x y
2
3
4
x y
2 1
1
x y2 4 ;
x y x
2
3 1
2
1
3 4
y ;
Представьте корень в виде степени.
1) 4 x ;
8
5) b ;
2) 6 ab7 ;
3
6
6) 3 ;
7
3) b ;
9
7) 3 3 ;
из 29 слайдов, слайд №
4) 5 3a 2b ;
5
8) 3 a ;
12
13.
Проверьте себя:1
1) x 4 ;
2) ab
5) b 4 ;
6) 9;
1
1
6;
3) b ;
3,5
7) 27;
из 29 слайдов, слайд №
1
4) 3a 2b 5 ;
5
8) a 3 ;
13
14.
Под корнем четной степени всегда стоит неотрицательное число.Под корнем же нечетной степени (2n+1) может стоять любое число, в том
числе и отрицательное. В этом случае, чтобы заменить корень на степень
минус «-» надо вынести перед корнем.
m
2 n 1 m
m
2 n 1
(a )
a a 2 n 1
Примеры:
4
3
1) a 4 a 3 ;
1
2) 7 b b 7 ;
5
3
5
3
5) 5 (a b) a b 4 ;
2
3) 3 8 2 8 3 ;
4) 3 p 21 p 7 ;
1
6) 11 x 2 y 3 x 2 y 3 11 ;
из 29 слайдов, слайд №
14
15.
Представьте корень в виде степени.1) x ;
7
2) ab ;
3
7
9
3) 7 3 ;
из 29 слайдов, слайд №
15
16.
Проверьте себя:1
1) x 7 ;
7
ab 6 ;
2)
9
3) 3 7 ;
из 29 слайдов, слайд №
16
17.
А если показатель отрицательный, тоm 0, n 0
n
a
m
n
a m a
m
n
1
m
an
Примеры:
В общем виде данное свойство выглядит:
a
p
1
p
a
.
Сравните со свойством степени с целым отрицательным показателем.
из 29 слайдов, слайд №
17
18.
1.Сформулируйте определение степени с отрицательным рациональнымпоказателем и запишите его аналитически.
2. Запишите, пользуясь этим определением, следующие степени в виде дробей:
1) 3
1
4;
2) 10
0,3
; 3) 8
2
3;
4) a
5
7;
5) b
1
3;
3. Запишите в виде степеней:
1)
1
1
b7
c5
; 2)
3
; 3)
1
1
;
0,9
m
из 29 слайдов, слайд №
18
19.
Проверьте себя:из 29 слайдов, слайд №
19
20.
Действия над степенями с дробными показателямивыполняются по тем же правилам, что и над степенями
с любыми целыми показателями, т. е. по правилам:
ат · аn = ат+n
(ат)n= ат·n
ат : аn= ат-n
(аbc)n= аn · bn · cn
n
a
b
an
bn
a n b m
n
m
b
a
из 29 слайдов, слайд №
20
21.
ат · аn = ат+nПримеры:
4)
из 29 слайдов, слайд №
21
22.
ат : аn= ат-nПримеры:
4)
из 29 слайдов, слайд №
22
23.
(ат)n= ат·nПримеры:
4)
из 29 слайдов, слайд №
23
24.
(аbc)n= аn · bn · cnПримеры:
1
1) (8a) 3
1
1 1
1 1
1
1 1
3
(8a) 3 8 3 a 3 2 3 3 a 3 2 3 a 3 2a 3
2)
из 29 слайдов, слайд №
24
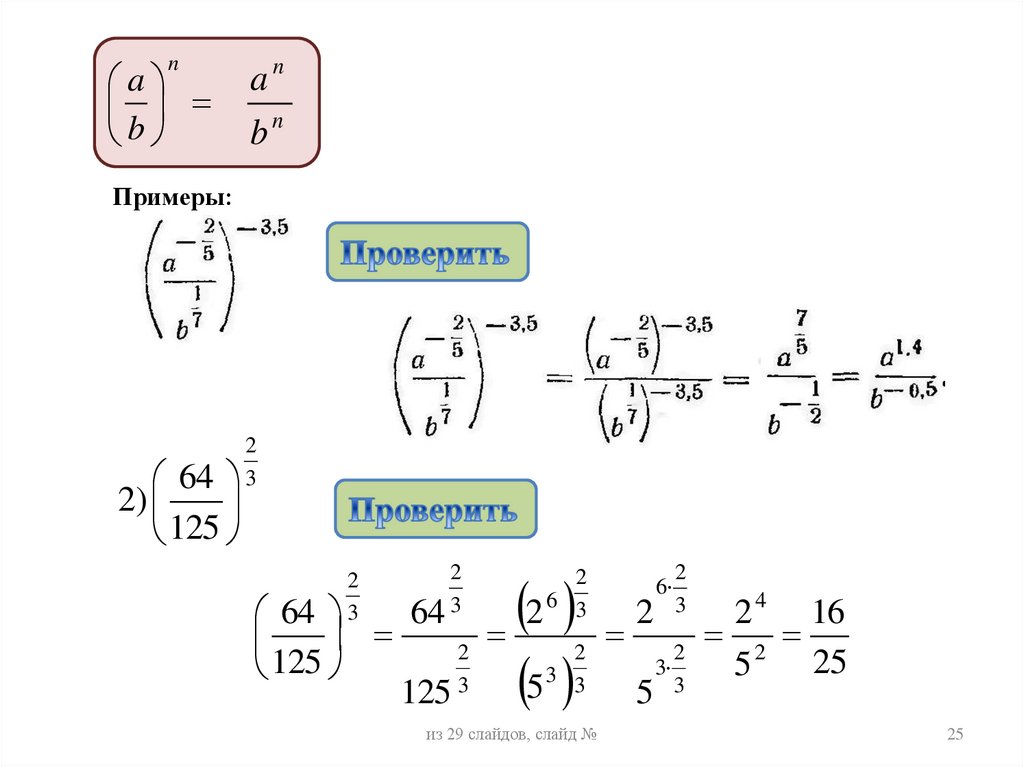
25.
na
b
an
bn
Примеры:
2
64 3
2)
125
2
125
5 5
125
2
64 3
2
64 3
2
26 3
2
3
2
3 3
из 29 слайдов, слайд №
6
2
3
2 4 16
2
2
25
3
5
3
25
26.
1. Можно ли при выполнении действий над степенями с дробными показателямипользоваться правилами действий над степенями с целыми показателями?
(Сначала производите действия
в скобках, десятичную дробь
замените на обыкновенную, числа
старайтесь представлять в виде
степени.)
Используйте формулы
сокращенного умножения
Основание степени каждого из сомножителей, стоящих в скобках, представьте в виде
степени числа 2.
из 29 слайдов, слайд №
26
27.
Проверьте себя:1. Можно. Правила действий над степенями с целыми и дробными показателями
одни и те же.
2.
4. 5
из 29 слайдов, слайд №
27
28.
При упрощении следующих примеров, корни замените на степени, составныечисла ( 32, 48, 81,16) представьте в виде степени или произведения степеней или
простых чисел, и только потом пользуйтесь свойствами степени.
1.
Выполните действия в скобках, а затем замените
дробь 0,4 на обыкновенную дробь
32 2 5
2.
48 2 4 3
3.
81 3 4
4.
16 2 4
из 29 слайдов, слайд №
28
29.
Проверьте себя:1. 2
16
;
2.
81
3. 1,5
4. 3
из 29 слайдов, слайд №
29




























 mathematics
mathematics








