339.89K

Category: $mathematics$ mathematics

Системы линейных алгебраических уравнений

1.

Лекция
Тема: «Системы линейных
алгебраических
уравнений»
10.09.2021
1

3.

План
Введение
1. Ранг матрицы
2. Общие сведения о СЛАУ
3. Решение СЛАУ
1) Метод Крамера
2) Метод Гаусса
3) Матричный метод
4. Теорема Кронекера – Капели
10.09.2021
4

4.

1. Эквивалентные матрицы.
ОПРЕДЕЛЕНИЕ.
Две матрицы
называются эквивалентными, если одна
получена из другой элементарными
преобразованиями СТРОК
10.09.2021
5

К элементарным преобразованиям СТРОК
матрицы относятся следующие:
1.
2.
3.
4.
Перестановка строк
Исключение строки, состоящей из
нулевых элементов
Умножение всех элементов какой-либо
строки число
Прибавление к каждому элементу одной
строки соответствующих элементов
другой строки, умноженной на любое
число
10.09.2021
6

6.

Ранг матрицы
ОПРЕДЕЛЕНИЕ. Наивысший порядок
k отличного от нуля определителя
матрицы A называется рангом
матрицы A и обозначается r(A)=k .
Причём (k m, k n)
10.09.2021
7

7.

Замечание
Ранг НУЛЕВОЙ матрицы (то есть все
элементы равны 0) и только ей РАВЕН
НУЛЮ
ЭКВИВАЛЕНТНЫЕ МАТРИЦЫ ИМЕЮТ
ОДИНАКОВЫЙ РАНГ
Если в каждой строке и в каждом столбце
матрицы находится не более одного
отличного от нуля элемента, то ранг
матрицы равен числу этих отличных от нуля
элементов.
10.09.2021
8

8.

Как найти ранг матрицы с
помощью метода Гаусса
1) с помощью элементарных
преобразований приводим матрицу к
ступенчатому виду
2) ранг матрицы равен количеству строк.
10.09.2021
9

9.

Пример. Найти ранг матрицы
0
0 -1
1
2
2
-1 3
A
2
0
0
3
4 12 8 8
Решение
Дана матрица «четыре на четыре»,
значит, её ранг не превзойдёт 4-х.
10.09.2021
10

10.

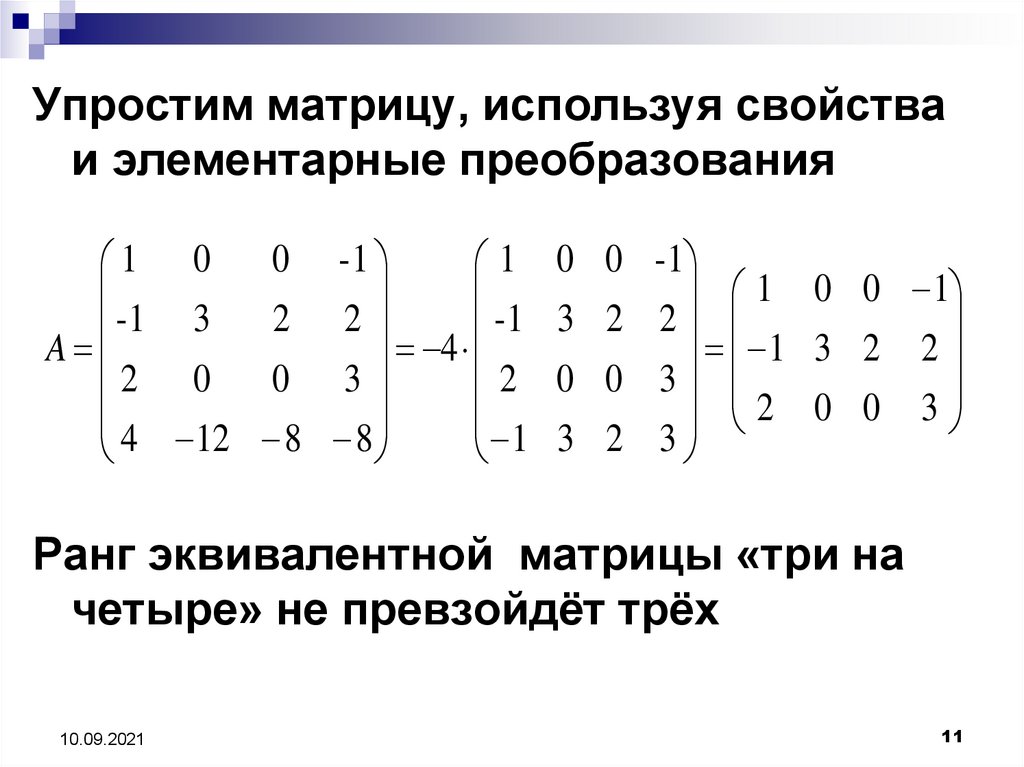
Упростим матрицу, используя свойства
и элементарные преобразования
0 -1
1 0
1
2 2
-1 3
-1
A
4
2 0
0 3
2
4 12 8 8
1
0 0 - 1
1 0 0 1
3 2 2
1 3 2 2
0 0 3
2 0 0 3
3 2 3
Ранг эквивалентной матрицы «три на
четыре» не превзойдёт трёх
10.09.2021
11

11.

Приведём последнюю матрицу
к ступенчатому виду
1 0 0 1 1 0 0 1 1 0 0 1
A 1 3 2 2 0 3 2 1 0 3 2 1
2 0 0 3 2 0 0 3 0 0 0 5
Для этого достаточно два шага:
1. Ко второй строке прибавим первую и «занулим»
элемент a21
2. Первую строку умножим на -2 и сложим с
третьей и «занулим» элемент a
31
10.09.2021
12

12.

Анализируем последнюю
матрицу
Матрица содержит три строки,
следовательно, её ранг равен трём:
r(A)=3
Ответ: Ранг матрицы
0
0 -1
1
2
2 равен трём: r(A)=3
-1 3
A
2
0
0
3
4 12 8 8
10.09.2021
13

13.

2. Общие
сведения о СЛАУ
Определение. Совокупность n линейных
уравнений a x a x a x b
11 1
12 2
1n n
1
a x a x a x b
21 1 22 2
2n n
2
an1 x1 an 2 x2 ann xn bn
называется системой линейных уравнений,
- коэффициенты при неизвестных,
ij
a
b1 , b2 , , bn - свободные члены уравнений системы.
10.09.2021
14

14.

Системе уравнений n n соответствует
определитель, составленный из
коэффициентов при неизвестных, т.н.
ГЛАВНЫЙ ОПРЕДЕЛИТЕЛЬ СИСТЕМЫ:
10.09.2021
a11
a12
a 21
a 22
a2n
a n1
an2
a nn
a1n
15

15.

Решением системы n n называется
такой набор значений неизвестных
x1 1 , x2 2 , , xn n ,
который удовлетворят каждому
уравнению системы
Две системы называются
эквивалентными, если решение одной
из них является решением другой и
наоборот
10.09.2021
16

16.

Эквивалентную систему можно получить
путём элементарных преобразований
Различают
элементарные
преобразования 4-х типов (аналогичные
элементарным преобразованиям строк
матрицы):
1.
2.
Перестановка двух строк.
Умножение обеих частей какого-либо
уравнения на число k 0
10.09.2021
17

17.

3. Прибавление к обеим частям одного
из уравнений системы обеих частей
другого уравнения этой системы,
умноженного на любое число.
4. Исключение из системы тривиального
уравнения, т. е. уравнения, имеющего
вид
0 x1 0 x2 0 xn 0.
10.09.2021
18

18.

Замечание:
СЛАУ может
иметь единственное решение
иметь бесконечное множество решений
(т. е. быть неопределённой)
не иметь решений (т.е. являться
несовместной)
10.09.2021
19

19.

3. Решение СЛАУ
1) Метод Крамера
ТЕОРЕМА или
правило Крамера для системы n n
Если главный определитель системы 0 ,
то решение существует и притом
единственное, которое находится по
следующим формулам:
n
1
2
x1
, x2
, , xn
,
10.09.2021
20

20.

Каждый из определителей
1 , 2 , , n
(дополнительный или побочный)
получается из главного определителя
заменой соответствующего
столбца на столбец свободных
членов данной системы.
10.09.2021
21

21.

Пример.
Решить систему линейных уравнений
x1 x2 x3 2
4 x1 2 x2 x3 4
9 x 3 x x 8
2
3
1
Решение
Решение находим по формулам Крамера
3
1
2
x1 , x2
, x3
10.09.2021
22

22.

Составим и вычислим определители:
главный
1 1 1
4 2 1 1 ( 1)
9 3 1
2
2 1
3 1
1 ( 1)
3
4 1
9 1
1 ( 1)
4
4 2
9 3
1 5 6 2 0
Т. к. 0 , то система имеет
единственное решение.
10.09.2021
23

23.

дополнительные
2 1 1
1 4 2 1 2( 1)
8 3 1
1 2 1
2 4 4 1 1( 1)
2
1 1 2
9 3 8
10.09.2021
2 1
3 1
1( 1)
4 1
8 1
9 8 1
3 4 2 4 1( 1)
2
2
4 1
8 1
( 2)( 1)
2 4
3 8
3
1( 1)
3
3
1( 1)
4 1
9 1
4 4
9 8
4
4 2
8 3
1( 1)
4
2 4 4 2
4 4
9 8
( 2)( 1)
4
4 10 4 2
4 2
9 3
4 4 12 4
24

24.

По формулам Крамера находим
корни уравнения
3
1
2 2
2
4
x1
1, x2
1, x3
2
2
2
2
Проверка
Подставляя найденные значения x1 , x2 , x3
в уравнения системы, получаем верные
равенства:
1 1 ( 2 ) 2
2 2
4
(
1
)
2
1
(
2
)
4
4 4 верно
9 ( 1) 3 1 ( 2) 8
8 8
10.09.2021
25

25.

Замечание
Несовместные и неопределённые
системы
Если главный определитель системы и все
дополнительные определители системы равны
нулю, то система имеет бесконечное множество
решений (или является неопределённой)
Если главный определитель системы равен нулю,
а хотя бы один из дополнительных определителей
отличен от нуля, то система не имеет решений (или
является несовместной)
10.09.2021
26

26.

Решение СЛАУ
2) Метод Гаусса
Наиболее общим способом
исследования и решения систем
уравнений является метод Гаусса
(метод последовательного исключения
неизвестных)
Замечание: методом Гаусса можно
решать ЛЮБЫЕ СИСТЕМЫ m
уравнений с n неизвестными, в том
числе и однородные.
10.09.2021
27

27.

Алгоритм метода
на примере СЛАУ с тремя
неизвестными
Решить СЛАУ
a11 x1 a12 x 2 a13 x3 b1
a 21 x1 a 22 x 2 a 23 x3 b2
a x a x a x b
32 2
33 3
3
31 1
10.09.2021
28

28.

1.
Составим главную (или основную)
матрицу системы из коэффициентов при
неизвестных
a a a
11 12 13
A a 21 a 22 a 23
a a a
31 32 33
2.
Составим расширенную матрицу системы,
добавив к матрице A столбец свободных
членов уравнений системы
10.09.2021
a11 a12 a13 b1
B a 21 a 22 a 23 b2
a a a b
31 32 33 3
29

29.

3. Выполняя элементарные преобразования,
приведём расширенную матрицу к
треугольному виду:
a11 a12 a13 b1
a11
B a 21 a 22 a 23 b2 0
a a a b
0
31 32 33 3
a12
a 22
a13
a 23
0
a 33
b1
b2
b3
4. Запишем систему уравнений, эквивалентную
данной
a11 x1 a12 x 2 a13 x3 b1
a11 x1 a12 x 2 a13 x3 b1
a11 x1 a12 x 2 a13 x3 b1
a
x
a
x
a
x
b
x 2 a 23
x3 b2
21 1
22 2
23 3
2 0 x1 a 22 x 2 a 23 x 3 b2 a 22
a x a x a x b
0 x 0 x a x b
a x b
32 2
33 3
3
31 1
2
33 3
3
1
33 3 3
10.09.2021
30

30.

5. Решаем систему обратным ходом «снизу
вверх»:
1
b1 a12 x 2 a13 x3
x
1
a11
a x a x a x b
11 1
12 2
13 3
1
1
x3
a
x
a
x
b
x
b2 a 23
22 2
2
23 3
2
a 22
b
x3 3
b3
a33
x3
a33
b3
b3
1
1
b2 a 23
a13
b
a
x1
1
12
a11
a 22
a33
a33
b3
1
x2
b2 a 23
a 22
a33
b3
x3
a33
10.09.2021
31

31.

Пример. Решить методом Гаусса систему
2 x1 x 2 3 x3 5
x1 2 x 2 2 x3 17
x x 3x 4
2
3
1
Составим расширенную матрицу
системы и приведем ее к треугольному
виду:
10.09.2021
32

32.

1. Составим расширенную матрицу
системы и приведем ее к
треугольному виду:
2 1 3 5 1 1 3 4 1 1 3 4 1 1 3 4
A 1 2 2 17 1 2 2 17 0 3 1 13 0 3 1 13
1 1 3 4 2 1 3 5 0 1 9 13 0 0 26 52
1 1 3 4
0 3 1 13
0 0 1 2
10.09.2021
33

33.

2. Запишем систему уравнений, эквивалентную
данной
x1 x 2 3 x3 4
3 x 2 x3 13
x 2
3
3. Решаем систему обратным ходом
x1 4 x2 3 x3
x1 4 x2 3 2
x1 x2 3 x3 4
1
1
3 x2 x3 13 x2 ( x3 13) x2 ( 2 13)
3
3
x 2
3
x3 2
x3 2
x1 4 ( 5) 6 x1 3
x2 5
x2 5
x 2
x 2
3
3
10.09.2021
34

34.

4. Делаем проверку
5. Записываем ответ
10.09.2021
35

35.

Решение СЛАУ
3) Матричный метод
Система уравнений
a11 x1 a12 x 2 a13 x3 b1
a 21 x1 a 22 x 2 a 23 x3 b2
a x a x a x b
32 2
33 3
3
31 1
в матричной форме имеет вид
AX B
10.09.2021
36

36.

В матричном уравнении
a11
A a 21
a
31
b1
B b2
b
3
x1
X x2
x
3
10.09.2021
a12
a 22
a32
a13
a 23
a33
- матрица коэффициентов при
неизвестных
- матрица-столбец свободных членов
- матрица – столбец неизвестных
37

37.

Решением матричного уравнения
AX B
является матрица
1
X A B
Замечание. Очевидно, что матричный метод
можно применить тогда и только тогда,
когда главный определитель системы
отличен от нуля
10.09.2021
38

38.

Алгоритм и пример решения
СЛАУ матричным методом
2 x1 x 2 3 x3 5
x1 2 x 2 2 x3 17
x x 3x 4
2
3
1
Запишем заданную систему уравнений в
матричном виде
AX B
10.09.2021
39

39.

Где матрицы A, XиB имеют вид:
2 1 3
A 1 2 2
1 1
3
x1
X x2
x
3
5
B 17
4
Решением системы является матрица
1
X A B,
если ГЛАВНЫЙ ОПРЕДЕЛИТЕЛЬ
СИСТЕМЫ ОТЛИЧЕН ОТ НУЛЯ
10.09.2021
40

40.

1.
Найдём главный определитель
системы:
2
1
1 2
1
1
3
2 2
3
2 2
1
3
1
1 2
1 3
3
1 2
1
1
2( 6 2) (3 2) 3(1 2) 16 1 9 26 0
Т.о. обратная матрица существует и
система имеет единственное решение
10.09.2021
41

41.

2. Составим обратную матрицу
A11
1
1
A A12
A13
A21
A22
a 23
A31
A32
A33
Для чего вычислим алгебраические
i j
дополнения Aij ( 1) M ij
10.09.2021
42

42.

A11 ( 1)
A12 ( 1)
1 1
1
1 2
A13 ( 1)
1 2
1 3
(1 3 2 1) 1
1 2
1
1
1
3
2
2
A31 ( 1) 3 3
2
2 3 2 1 8
3
1 3
A31 ( 1) 3 1
2 2
1
1 2
1 1 2 1 3
1 2 ( 3) ( 2) 4
A21 ( 1) 2 1
1 3
1 3
A22 ( 1) 2 2
A23 ( 1)
A32 ( 1)
2 3
1
2 3
3 2
(1 3 ( 3) 1) 6
3
2 1
1 1
2 3
1
2
2 3 ( 3) 1 9
(2 1 1 1) 1
(2 2 ( 3) 1) 7
2 ( 2) 1 1 5
Обратная матрица системы имеет вид:
10.09.2021
8 6 4
1
1
A
1 9 7
26
3
1
5
43

43.

3. Найдем решение системы
1
X A B
8 6 4 5
( 8) ( 5) ( 6) 17 ( 4) 4
1
1
X
1 9 7 17
( 1) ( 5) 9 17 ( 7) 4
26
26
3
1
5
4
3
(
5
)
(
1
)
17
(
5
)
4
78 3
1
130 5
26
2
52
4. Сделаем проверку
2 3 ( 5) 3 2 5 6 5 6 5
5 5
3
2
(
5
)
2
2
17
3
10
4
17
17 17 верно
3 ( 5) 3 2 4
3 5 6 4
4 4
10.09.2021
44

44.

5.
Запишем ответ:
3
X 5 или
2
10.09.2021
x1 3, x2 5, x3 2
45

45.

4. Теорема Кронекера –
Капелли
Система линейных алгебраических уравнений
СОВМЕСТНА тогда и только тогда, когда ранг
её основной матрицы равен рангу её
расширенной матрицы,
причём система ИМЕЕТ ЕДИНСТВЕННОЕ
РЕШЕНИЕ, если ранг равен числу
неизвестных,
и БЕСКОНЕЧНОЕ МНОЖЕСТВО РЕШЕНИЙ,
если ранг меньше числа неизвестных
10.09.2021
46

46.

Замечание.
Данная теорема формулирует критерий
совместности системы линейных
алгебраических уравнений
10.09.2021
47

47.

Пример. Исследовать СЛАУ и
найти её решение
x1 x2 x3 x4 x5 0
x x x 2x x 0
1 2 3
4
5
x1 2 x2 x3 x4 2 x5 0
x1 2 x2 x3 2 x4 4 x5 0
Во-первых, очевидным решением
данной однородной системы является
нулевое решение: x1 x2 x3 x4 x5 0
10.09.2021
48

48.

Найдём ненулевые решения
системы
Найдём ранги основной и расширенной
матриц
10.09.2021
49

49.

1
1
B
1
1
1 1 1
1 0 1
1 1 2 1 0 0
2 1 1 2 0
0
2 1 2 4 0 0
1 1 1
0 1
0 2 1 2 0 0
1 2 2 1 0
0
1 0 3 3 0 0
1
1 1
0
1 2 2 1 0
0 2 1 2 0
0 2 1 2 0
1
1
1 0
1 1 1 1
B 0 1 2 2 1 0
0 0 2
1
2
0
Система совместна, т.к. ранг
расширенной матрицы равен рангу
основной матрицы и равен трём:
r(A)=r(B)=3
10.09.2021
50

50.

А так как ранг основной матрицы
меньше числа неизвестных (n=5), то
система имеет бесконечное множество
решений.
Вернемся теперь к системе уравнений,
полученной путём элементарных
преобразований:
x1 x2 x3 x4 x5 0
x2 2 x3 2 x4 x5 0
2 x3 x4 2 x5 0
10.09.2021
51