742.50K

Category: $mathematics$ mathematics

Системы линейных алгебраических уравнений

1.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Лекция 5
СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ
УРАВНЕНИЙ
С Л А У

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Дана система линейных алгебраических уравнений
Ax b , где
A - вещественная квадратная матрица порядка n,
b (b1 , b2 ,..., bn )T - заданный вектор,
x ( x1 , x2 ,..., xn )T - искомый вектор.
Предполагается, что det A 0. Тогда для каждого
вектора b система имеет единственное решение.

3.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Вид системы в развернутом виде:
a11 x1 a12 x2 ...a1n x b1
a21 x1 a22 x2 ...a2 n x b2
.......................................
a1n x1 a2 n xn ...ann x bn .

4.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Если задана некоторая произвольная система
уравнений, то без предварительного исследования
нельзя сказать, имеет ли она какое-либо решение
и, в случае, если решение существует, является
ли оно единственным.На этот вопрос существует
три ответа.
1. Решение системы уравнений существует и
является единственным. Например,
2 x y 4
x y 1.

5.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
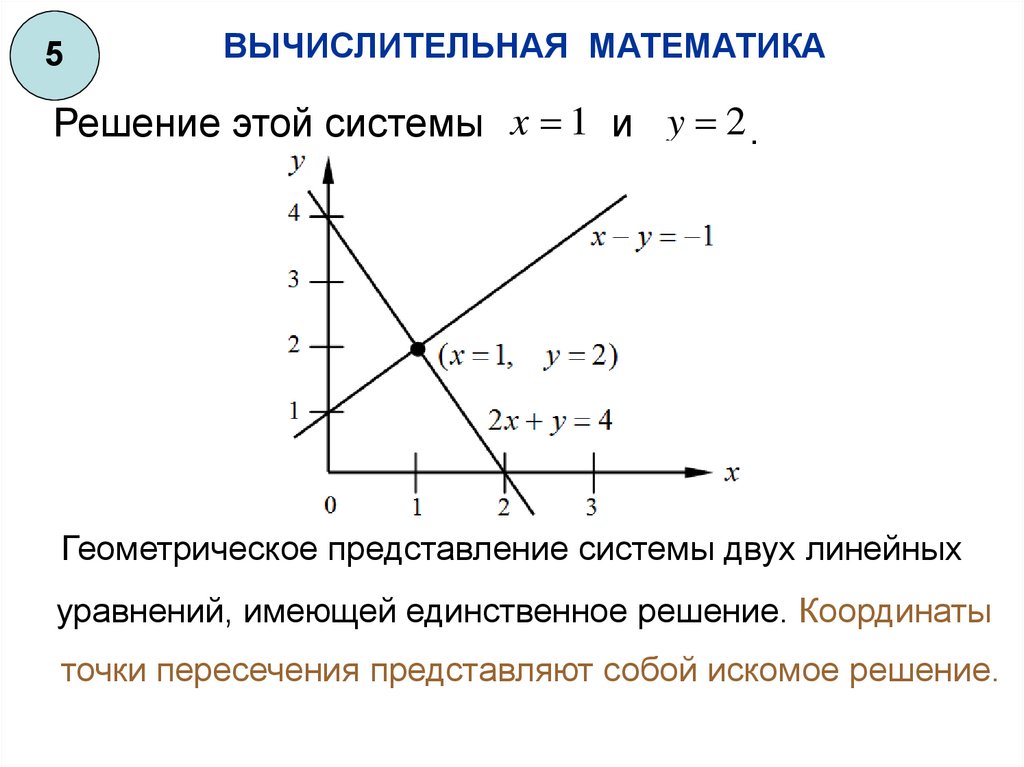
Решение этой системы x 1 и y 2 .
Геометрическое представление системы двух линейных
уравнений, имеющей единственное решение. Координаты
точки пересечения представляют собой искомое решение.

6.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Система уравнений вообще не имеет решения.
4 x 6 y 10
2 x 3 y 6.
Две прямые параллельны,
они нигде не пересекаются,
и система не имеет решения.
Геометрическое представление системы двух линейных
уравнений, не имеющей решения.

7.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
3. Система уравнений имеет бесконечное
множество решений
Два уравнения описывают
одну и ту же прямую линию.
Любая точка, лежащая на
этой линии, является
решением этой системы.
Геометрическое представление системы двух линейных
уравнений, имеющей бесконечное множество решений

8.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Две последние
системы уравнений называются
вырожденными. С точки зрения обычной математики
линейных уравнений всегда является или вырожденной
или невырожденной. С точки же зрения вычислений могут
существовать почти вырожденные системы, при решении
которых получаются недостоверные значения неизвестных.
Рассмотрим систему уравнений:
5 x 7 y 12
7 x 10 y 17.

9.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Эта система имеет единственное решение x 1, y 1.
Теперь рассмотрим пару значений x 2.415, y 0.
При подстановке этих значений в исходные уравнения
получаем
5 x 7 y 12.075
7 x 10 y 16.905.
После округления до двух
значащих цифр правые
части равенств совпадают
с правыми частями исходных уравнений. Дело в том, что
две прямые линии, описываемые двумя уравнениями этой
системы, почти параллельны.
Системы такого типа называются плохо обусловленными.

10.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Методы решения СЛАУ подразделяются на
• прямые (конечные, точные);
• итерационные (бесконечные, приближенные).
Прямые:
Итерационные:
Гаусса
Простых итераций
LU-разложений
Зейделя
Жордано
Квадратного корня
Релаксаций

11.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
МЕТОД
ГАУССА
Метод основан на идее последовательного
исключения неизвестных. Введем n 1
множителей
a i1
mi
, i 2, 3,..., n
a11
и вычтем из каждого уравнения первое,
умноженное на mi

12.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Обозначая
a1ij aij mi a1 j , i 2, 3,..., n,
bi1 bi mi bi ,
j 2,3,...., n,
для всех уравнений, начиная со второго, получаем
a1i1 0, i 2, 3,..., n.
Преобразованная система запишется в виде:
a11 x1 a12 x2 ...a1n x b1
0
a x ...a
1
22 2
1
2n
x b
1
2
.......................................
0
a12 n xn ...a1nn x bn1 .

13.

ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
5
Продолжая таким же образом на некотором k -м
этапе мы исключаем x k с помощью множителей
( k 1)
i
m
Тогда
( k 1)
ik
( k 1)
kk
a
a
(k )
ij
a
akk( k 1) 0.
, i k 1,..., n,
( k 1)
ij
a
( k 1) ( k 1)
i
kj
m
a
bi( k ) bi( k 1) mi( k 1)bk( k 1)
,
k 1, ..., n 1.
При k n 1 происходит исключение x n 1
из последнего уравнения.

14.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Окончательная треугольная система уравнений
записывается следующим образом:
a11 x1 a12 x2 ...a1n x b1
x2 ...a2 n x b2
a22
.......................................
a n 1nn x f n 1n .
Такая система уравнений называется треугольной.
Приведение матрицы к треугольной называется
прямым ходом.

15.

ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
5
Треугольная система легко решается обратным
ходом по следующим формулам:
bn( n 1)
xn ( n 1) ,
ann
xj
(f
( j 1)
j
a
xn 1
( j 1)
jn
n
( j 1)
jj
b
x ... a
a
( n 2)
n 1
( n 2)
n 1,n n
( n 2)
n 1,n 1
a
a
( j 1)
j , j 1
x j 1 )
x
, ... ,
, j n 2, n 3,..., 1.
В результате получаем искомое решение.

16.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Вычисление определителя методом Гаусса
Для вычисления определителя матрицы
A
решаем систему Ax b и выполняем прямой
ход метода Гаусса:
det A a11 a
(1)
22
a
( 2)
33
... a
( n 1)
nn
.

17.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Метод
LU – р а з л о ж е н и й
Пусть A — данная матрица, а L и U - нижняя
(левая) и верхняя (правая) треугольные матрицы:
1 0
l21 1
L
... ...
ln1 ln 2
...
...
...
...
0
0
...
1
u11 u12
0 u
22
U
... ...
0
0
... u1n
... u2 n
... ...
... unn

18.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Справедливо следующее утверждение:
Если все главные миноры квадратной матрицы
A отличны от нуля, то существуют такие
нижняя L и верхняя U треугольные матрицы,
что A LU .
Если элементы диагонали одной из матриц L или U
фиксированы (ненулевые), то такое разложение
единственно.

19.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Перемножая нижнюю и верхнюю матрицы
приходим к матрице уравнений размерностью n*n :

20.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Элементы матриц L и U могут быть вычислены
с помощью следующих формул:
i 1
uij aij lik ukj
(i j ),
k 1
j 1
1
lij aij lik ukj (i j ).
k 1
u jj

21.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Запишем исходную систему Ax b так: LUx b .
T
Введем вспомогательный вектор y y1, y 2 ,..., y n
решение системы сводится к решению двух систем с
треугольными матрицами коэффициентов:
Ly b,
Ux y.
Запишем уравнение Ly b в развернутом виде:

22.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Все yi могут быть найдены по формуле:
i 1
yi bi lik yk , i 1, 2,..., n.
k 1
Развернем теперь векторно-матричное уравнение Ux y
u11 x1 u12 x2 ... u1n xn y1
u x ... u x y
22 2
2n n
2
.......... .......... .....
u nn xn y n
Значения неизвестных xi находятся в обратном порядке:
n
1
xi yi uik xk ,
uii
k i 1
i n, n 1,...,1

23.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Метод
Жордано
1. Выбирается первая колонка слева, в которой
есть хоть одно отличное от нуля значение.
2. Если самое верхнее число в этой колонке есть
нуль, то меняется вся первая строка матрицы с
другой строкой матрицы, где в этой колонке нет
нуля.
3. Все элементы первой строки делятся на
верхний элемент выбранной колонки.

24.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
4. Из оставшихся строк вычитается первая строка,
умноженная на первый элемент соответствующей
строки, с целью получить первым элементом
каждой строки (кроме первой) нуль.
5. Далее проводим такую же процедуру с матрицей,
получающейся из исходной матрицы после
вычёркивания первой строки и первого столбца.
6. После повторения этой процедуры n-1 раз
получаем верхнюю треугольную матрицу.

25.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
7. Вычитаем из предпоследней строки последнюю
строку, умноженную на соответствующий
коэффициент, с тем, чтобы в предпоследней
строке осталась только 1 на главной диагонали.
8. Повторяем предыдущий шаг для последующих
строк. В итоге получаем единичную матрицу и
решение на месте свободного вектора (с ним
необходимо проводить все те же преобразования).

26.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Пример.
Решить следующую систему уравнений:
2 x1 x2 x3 2
3 x1 x2 2 x3 3
x
x3 3
1
.
Прямой ход
Исключим переменную x1 из всех уравнений, за
исключением первого. Поменяем местами 1 и 3 уравнения
(порядок уравнений в системе не имеет значения).

27.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
x3 3
x1
3x1 x2 2 x3 3
2x x x 2
1 2 3
1 0 1
3 1 2
2 1 1
3
3
2
Из уравнения 2 вычитаем уравнение 1, умноженное на 3.
x3 3
x1
x2 5 x3 6
2x x x 2
1
2
3
1
1 0
0 1 5
2 1 1
3
6
2

28.

ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
5
Из уравнения 3 вычитаем уравнение 1, умноженное на 2.
1
3
1 0
x3 3
x1
x2 5 x3 6
0 1 5 6
x2 3 x3 4
0 1 3 4
Исключим переменную x2 из последнего уравнения.
Из уравнения 3 вычитаем уравнение 2.
x1
x3 3
x2 5 x3 6
2 x3 2
1 0
0 1
0 0
1
5
2
3
6
2

29.

ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
5
Обратный ход.
Коэффициенты уравнения 3 разделим на 2.
x1
x3 3
x2 5 x3 6
x3 1
1
1 0
0 1 5
0 0
1
3
6
1
Исключим переменную x3 из 1 и 2 уравнений.
Из уравнения 1 вычитаем уравнение 3.
x1
2
x2 5 x3 6
x3 1
0
1 0
0 1 5
0 0
1
2
6
1

30.

ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
5
К уравнению 2 прибавим уравнение 3, умноженное на 5.
x1
x2
2
1
x3 1
Получаем решение:
1 0
0 1
0 0
x1 2
x2 1
x3 1 .
0
0
1
2
1
1

31.

ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
5
Вычисление элементов обратной матрицы
Обратной к матрице A называют такую матрицу
A для которой A A A A E , где
1
1 0 ... 0
0 1 ... 0
E
.
. . ... .
0 0 ... 1
1
a11 a12
a21 a22
A
.
.
an1 an 2
1
... a1n
x11
... a2 n
x21
1
. A
.
... .
... ann
xn1
x12
x22
.
xn 2
... x1n
... x2 n
... .
... xnn
Для вычисления элементов обратной матрицы A
используем соотношение
A A 1 E.
1

32.

ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
5
1
A
Умножая матрицу A на
и приравнивая каждый элемент
произведения соответствующему элементу матрицы E
2
неизвестными
n
получим систему из n уравнений с
2
xij
(i, j 1,2,..., n).
Так, умножая почленно каждую строку матрицы A на
первый столбец матрицы A
1
и каждый раз приравнивая
полученное произведение соответствующему элементу
первого столбца матрицы E , получаем систему

33.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
a11 x11 a12 x21 a13 x31 ... a1n xn1 1,
a21 x11 a22 x21 a23 x31 ... a2 n xn1 0
......................................................
an1 x11 an 2 x21 an 3 x31 ... ann xn1 0

34.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Аналогично при умножении строк матрицы A на второй
столбец матрицы A
1
образуется еще одна система
a11 x12 a12 x22 a13 x32 ... a1n xn 2 0,
a21 x12 a22 x22 a23 x32 ... a2 n xn 2 1
......................................................
an1 x12 an 2 x22 an 3 x32 ... ann xn 2 0
и так далее…

35.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Метод прогонки

36.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА

37.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА

38.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА

39.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА

40.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА

41.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Итерационные методы решения СЛАУ
Дана система линейных алгебраических уравнений
a11 x1 a12 x2 ... a1n xn b1
a x a x ... a x b
21 1 22 2
2n n
2
, det A 0
....................................................
an1 x1 an 2 x2 ... ann xn bn
Для построения итерационных формул нужно систему
привести к виду: X C X , где

42.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
x1
x2
X
xn
0
a21
a
C 22
...
an1
a
nn
a12
a11
...
0
...
...
an 2
ann
...
...
a1n
b1
a
a11
11
a2 n
b2
a22 a22
...
bn
0
a
nn

43.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
В результате получаем:
a1,n
b1 a1,2
x1
x2 ...
a1,1 a1,1
a1,1
a2,1
a2,n
b2
x2
x1 ...
a2,2 a2,2
a2,2
..............................................
an,1
an,n 1
bn
xn
x1 ...
xn 1.
an,n an,n
an,n

44.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Далее справа подставляем предыдущие приближения
X k начиная с X 0 и слева получаем последующие
приближения X
k 1
.
В результате получаем итерационные формулы вида:
X
( k 1)
C X
(k )
Начиная с X 0, получим последовательность векторов
X 0 , X 1 , X 2 ,..., X k ,... Если эта последовательность сходится,
то она сходится к решению системы.
В результате получаем формулы метода итерации.

45.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Метод простой итерации
a1,n ( k )
b1 a12 ( k )
( k 1)
x1
x2 ...
xn
a11 a11
a11
( k 1)
2
x
a2,n ( k )
b2 a21 ( k )
x1 ...
xn
a22 a22
a22
.............................................................
an ,n 1 ( k )
bn an ,1 ( k )
( k 1)
xn
x1 ...
xn 1.
ann ann
ann
Или иначе:
n a
b
i, j k
k 1
i
xi
xj
ai ,i j 1 ai ,i
j i

46.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Эти формулы используем при k 0, 1,... и получаем
последовательность векторов X 0 , X 1 , X 2 ,..., X k .
0
X
За начальный вектор
будем брать столбец свободных
членов или X 0 0.
Условие окончания поиска:
k 1
i
x x
k
i
, i 1..n
Достаточные условия сходимости метода:
n
n
aii aij
j 1
или
a jj aij
i 1
Если условия выполнены, то процесс простой итерации
сходится к единственному решению системы независимо
от выбора начального приближения.

47.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА

48.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Метод Зейделя
Идея метода Зейделя заключается в том, что
при вычислении (k 1) -го приближения
неизвестной xi учитываются уже вычисленные
ранее (k 1) -е приближения неизвестных
x1 , x2 , ..., xi 1
Итерационные формулы метода Зейделя будут
иметь следующий вид:

49.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
n a
b
1 j (k )
( k 1)
1
x1
xj ,
a11 j 2 a11
n a
b
a
2 j (k )
x2( k 1) 2 21 x1( k 1)
xj ,
a22 a22
j 3 a22
...........................................................
a
n 1 nj x ( k 1) ,
bn
( k 1)
xn
ann j
k 0, 1, 2,...
ann j 1
Или иначе:
i 1 a
n a
b
i , j k 1
i, j k
k 1
i
xi
xj
xj
ai ,i j 1 ai ,i
j i 1 ai ,i

50.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Условия сходимости метода Зейделя те же, что у
метода простой итерации : преобладание диагональных
элементов.
Для метода Зейделя имеется еще теорема о сходимости:
Пусть матрица A — вещественная, симметричная,
определенная матрица. Тогда метод Зейделя
сходится.

51.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Метод релаксации (ослабления)
Пусть имеем систему линейных уравнений
a11 x1 a12 x2 ...a1n xn b1
a 21 x1 a 22 x2 ...a 2 n xn b2
.......... .......... .......... .......... .
a n1 x1 a n 2 x2 ...a nn xn bn
Преобразуем эту систему с.о.: перенесем правую часть
налево и разделим первое уравнение на a11, второе на
a 22 и т.д. Тогда получим систему, приготовленную к
релаксации:

52.

5
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
x1 c12 x2 ... c1n xn d1 0
c21 x1 x2 ... c2 n xn d 2 0
.......... .......... .......... .......... .........
cn1 x1 cn 2 x2 ... xn d n 0
где
cij
aij
aii
(i j ),
bi
di
aii

53.

ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
5
Пусть x
(0)
( x1( 0) ,
x2( 0) , ..., xn( 0) ) - начальное
приближение решения системы. Подставляя эти значения
в систему, получим невязки
n
(0)
1
d1 x
c1 j x
(0)
2
d2 x
c2 j x
R
R
(0)
1
(0)
2
j 2
n
j 1,
j 2
(0)
j
(0)
j
.......... .......... .......... .......... ..
n 1
Rn( 0 ) d n xn( 0 ) cnj x (j0 )
j 1