Similar presentations:
Системы линейных алгебраических уравнений (лекция 1)
1.
Лекция 1. Системы линейныхалгебраических уравнений
Мустафина Ляззат Мухамеджановна
Доцент кафедры Высшая математика
2.
План лекции1. Системы линейных алгебраических уравнений. Определители.
Формулы Крамера
2. Матричный способ решения систем линейных уравнений
3. Ранг матрицы.
4. Метод Гаусса решения систем линейных уравнений
3.
4.
1. Системы линейных алгебраических уравнений. ФормулыКрамера
Определение 1. Системой m линейных алгебраических уравнений с n
неизвестными называется система уравнений вида
а11 х1 а12 х2 ... а1п хп b1
а х а х ... а х b
21 1
22 2
2п п
2
..........................................
аm1 х1 аm 2 х2 ... аmп хп bm
(1)
Определение 2. Решением системы (1) называется совокупность чисел
x1 1 , x2 2 , ... ,
xn n ,
которые при подстановке в систему все уравнения обращают в тождества.
5.
Примеры:2 х1 3х2 7
а)
3х1 7 х2 1
2 x1 x2 3 x3 4
б) x1 3 x2 x3 11
x 2 x 2 x 7
2
3
1
x1 2 x2 4 x3 x4 3
в) 2 x1 3 x2 5 x3 3 x4 1
3x 5 x x 4 x 2
2
3
4
1
6.
1.1. Системы двух линейных уравнений с двумя неизвестнымиРассмотрим систему
a1 x b1 y c1
.
a2 x b2 y c2
С помощью исключения неизвестных, систему можно привести к виду:
a1b2 a 2 b1 x b2 c1 b1c2
.
a1b2 a2 b1 y a1c2 a2 c1
7.
Если ввести обозначенияa1
a1b2 a2b1
a2
c1
b1
, x b2 c1 b1c2
c2
b2
Система перепишется в виде:
x x
y .
y
a1
b1
, y a1c2 a2 c1
a2
b2
c1
.
c2
8.
Возможны следующие случаи решения этой системы:1. если 0 - система имеет единственное решение.
y
x
, y
.
Решение находится по формулам Крамера: х
2. если 0 и х 0 или у 0 - система не имеет решений.
3. если 0 , х 0 и у 0 - система имеет бесчисленное множество
решений.
9.
Определение 1. Определителем второго порядка называется число,получающееся из квадратной таблицы, по следующему правилу:
a11 a12
a11 a 22 a12 a21 .
a21 a22
2 5
2 4 5 3 8 15 7
Пример 1.
3 4
7 6
7 2 6 3 14 18 4
Пример 2.
3 2
10.
1.2. Системы трех линейных уравнений с тремя неизвестнымиОпределение 2. Определителем третьего порядка называется число,
получающееся из квадратной таблицы, по следующему правилу:
a11 a12
a21 a22
a31 a32
a13
a23
a33
a11 a 22 a33 a12 a23 a31 a13 a 21 a32 a13 a22 a31 a12 a 21 a33 a11 a23 a32
a11 a 22 a33 a12 a23 a31 a13 a 21 a32 a13 a22 a31 a12 a 21 a33 a11 a23 a32
11.
Вычисления проводят по схеме:2 5 1
Пример 3. 3 4 1 2 4 3 5 1 6 3 2 1
6 2 3
6 4 1 3 5 3 2 1 2 24 30 6 24 45 4 12 65 53
12.
Рассмотрим систему:a1 x b1 y c1 z d1
a 2 x b2 y c 2 z d 2
a x b y c z d
3
3
3
3
a1 b1 c1
Положим a 2 b2 c 2 0 .
a 3 b3 c3
13.
Тогда решение системы можно найти по формулам Крамера:y
x
z
х
, y
, z
, где
d1 b1
x d 2 b2
d 3 b3
c1
c2
c3
a1 d1
y a2 d 2
a3 d 3
c1
c2
c3
a1 b1
z a 2 b2
a3 b3
d1
d2
d3
14.
2. Матричный способ решения систем линейных уравненийОпределение 1. Матрицей размерности m n называется прямоугольная
таблица из m n чисел, расположенных в т строках и п столбцах.
Обозначаются матрицы, как правило, большими буквами A, B, C,...,
a11 a12 ... a1п
a
a
...
a
22
2п
21
A
... ... ... ...
a
a
...
a
тп
т2
т
или A aij ~ m n
Например, матрица A 2 1 2 имеет размерность 2×3: 2 строки и 3
4
столбца.
3
5
15.
2.1. Виды матриц1) Квадратная матрица. Матрица, имеющая одинаковое число строк и
столбцов, размерности п×п, называется квадратной матрицей порядка п.
3 4
A
1 2
Элементы
0 1 1
B 2 0 3
1 1 1
a11 , a22 ,...,ann
квадратной
матрицы
А
называются
диагональными элементами (или говорят, что они лежат на главной диагонали
матрицы).
16.
2) Матрица – строка - это матрица размера1×пA (a11 ,..., a1n ) .
3) Матрица – столбец - это матрица размера m×1
b11
b21 .
B
...
bm1
17.
4) Треугольная матрица – это квадратная матрица, в которой элементы,расположенные под диагональю (или над диагональю), равны нулю.
a11
0
A
.
0
a12
a 22
.
0
... a1n
1 2
... a 2 n ,
0 3
B
... .
0 0
... a nn
0 0
3 4
0 0
2
0 1 , C 1 1 0 .
2 3 0
1 2
0 7
5) Нулевая матрица - это матрица, все элементы которой равны нулю.
Нулевая матрица обозначается символом O .
18.
6) Единичная матрица. Квадратная матрица, все диагональные элементыкоторой равны 1, а остальные – нулю, называется единичной и обозначается
E или En , где п ее порядок. Таким образом,
1 0... 0
E 0 1... 0
0 0... 1
Определение 2. Две матрицы называются равными, если
1) матрицы имеют одинаковые размерности;
2) элементы, стоящие на соответственных местах этих матриц, равны.
19.
2.2. Действия над матрицами1) Умножение матрицы на число
Определение 3. Чтобы умножить число на матрицу A или матрицу A
на число , нужно умножить на все элементы матрицы A . Очевидно,
A A .
1 5
Пример 4. Пусть A 3 2 . Найти матрицы 2А, -3А.
4 6
20.
2). Сложение матрицОпределение 4. Суммой двух матриц A (aij ) ~m×n и B (bij ) ~m×n одной
размерности называется матрица
C (cij ) ~m×n той же размерности
(обозначается C A B ), элементы которой определяются равенствами:
сij aij bij , i 1,..., m; j 1,..., n .
2 5 3
0 4 2
, B
.
Пример 5. Пусть A
4 1 6
5 2 3
Найти матрицы А+В, А-В, 2А-3В.
21.
3) Умножение матрицОпределение 5. Пусть заданы две матрицы A и B, причем число столбцов
первой из них равно числу строк второй:
a11
a 21
A
.
a
m1
a12
a 22
.
am2
... a1 p
b11 b12
... a 2 p
b21 b22
, B
... .
.
.
b
... a mp
p1 b p 2
... b1n
... b2 n
.
... .
... b pn
22.
Положим cij ai1b1 j ai 2b2 j ... aipb pj (i 1,..., m; j 1,..., n) . Матрицаc11
c21
C
...
c
m1
c12
c22
...
cm 2
... c1n
... c2 n
... ...
... cmn
называется произведением А на В и обозначается АВ.
23.
Замечание. Размерность произведения матриц можно определить поправилу, которое в дальнейшем будет называться правилом умножения
размерностей: (m р)( р п) m п .
0 4
4 2
.
и B
Пример 6. Пусть A
5 2
3 1
Найти произведение матриц А∙В и В∙А.
24.
Таким образом, мы можем сделать важный вывод: при перемноженииматриц нельзя менять порядок сомножителей (произведение матриц не
коммутативно).
3 4 2
Пример 7. Пусть А 3 1 6
Найти произведение А∙В.
2 5
В 1 4 .
3 4
25.
4) Транспонирование матрица11
Рассмотрим
произвольную матрицу Определение 6. Матрица AТ a12
а11
а21
A
.
а
m1
а12
а22
.
аm 2
... а1n
... а2 n
... .
... аmn
.
a
1n
а 21
a 22
.
a2n
... а m1
... a m 2
,
... .
... a mn
получающаяся из A заменой строк столбцами,
называется транспонированной к A .
6 2 3
Пример 8. Дана матрица А 4 5 1 . Найти матрицу АТ.
26.
5) Нахождение обратных матрицОпределение 7. Квадратная матрица A 1 называется обратной к матрице
A , если имеет место равенство: A А 1 А 1 A E.
Определение 8. Квадратная матрица A называется невырожденной, если
ее определитель отличен от нуля, и вырожденной в противном случае.
27.
Теорема 1. Для того чтобы матрица A aij имела обратную матрицу,необходимо и достаточно, чтобы она была невырожденной. При этом обратная
матрица находится по формуле:
A11
1
~T
A21
1
~
A
(A) , где A
...
detA
A
n1
A12
A22
...
An 2
... A1n
... A2 n
.
... ...
... Ann
~
Матрица A называется присоединенной, элементами этой матрицы являются
алгебраические дополнения соответствующих элементов матрицы А.
28.
Находить обратную матрицу будем по схеме:1. Размерность п п - квадратная матрица
2. А detA 0 - невырожденная матрица
~
3. Найти матрицу A - присоединенная матрица
~T
4. Найти матрицу A - транспонированная матрица
5. Записать матрицу A
1
1 ~T
(A )
detA
29.
2.3. Решение систем п линейных уравнений с п неизвестнымиматричным способом
Рассмотрим систему
а11 х1 а12 х2 ... а1п хп b1
а х а х ... а х b
21 1 22 2
2п п
2
..........................................
ап1 х1 ап 2 х2 ... апп хп bm
(2)
Введем три матрицы для системы (1):
a11 a12 ... a1n
x1
a
a
...
a
x
22
1n
21
А
. , X 2
...
.
. ... .
a
x
п1 aп 2 ... aпn
n
и
b1
b2
B
...
b
п
30.
Матрица А, составленная из коэффициентов системы, называетсяматрицей системы.
Х - матрица-столбец неизвестных;
В - матрица-столбец свободных членов.
Тогда, используя правило умножения матриц, систему можно записать
в матричной форме:
A X B.
31.
Если А det A 0. Тогда матрица А имеет обратную. Следовательно,решение системы запишется в виде X A 1 B.
Действительно, умножая матичное уравнение A X B на обратную
матрицу А-1 слева, получим
A 1 А Х A 1 В Е Х A 1 В X A 1 B
Такой способ решения системы линейных уравнений называется
матричным.
32.
3. Ранг матрицыМинором k -го порядка матрицы A называется определитель,
образованный элементами, расположенными на пересечении каких-либо k
строк и каких-либо k столбцов.
Пусть A - матрица размера m n . Если матрица A нулевая, то ее ранг равен
нулю. Если матрица A ненулевая, то ее рангом называется наибольший
порядок r минора, отличного от нуля.
33.
Ступенчатой матрицей будем называть матрицу, удовлетворяющуюследующим двум условиям:
1) все нулевые строки находятся ниже всех ненулевых;
2) у каждой ненулевой строки, кроме первой, число нулевых элементов,
предшествующих первому ненулевому, больше, чем у предыдущей строки.
1 2 1
A 0 0 2
0 0 0
0 3
5 1
0 0
3
0
B
0
0
2 1 0 4 5
0 2 1 0 0
0 0
2 5 1
0 0 0 0 0
Ранг ступенчатой матрицы равен числу ее ненулевых строк.
34.
Элементарные преобразования матрицы:1) перестановку строк;
2) умножение какой-либо строки на число, отличное от нуля;
3) сложение строк;
4) те же операции со столбцами.
Матрицы,
полученные
одна
из
другой
элементарными
преобразованиями, называются эквивалентными.
Эквивалентность матриц А и В обозначается символом ~: А~В.
Элементарные преобразования матрицы не меняют ее ранга.
35.
4. Метод Гаусса решения систем линейных уравненийРассмотрим систему линейных алгебраических уравнений общего вида
a11x1 a12 x2 ... a1n xn b1
a x a x ... a x b
21 1 22 2
2
2n n
...............................................
am1 x1 am 2 x2 ... amn xn bm
Обозначим
a11 a12 ... a1n b1
a11 a12 ... a1n
a21 a22 ... a2n b2
a21 a22 ... a2 n
, A ( A | B)
А
.
. ... .
.
.
... .
.
.
a
a a
b
a
...
m
mn
2
m
m1
m1 am 2 ... amn
(1)
36.
Определение 3. Система называется совместной, если она имеет хотя быодно решение, и несовместной в противном случае.
Определение 4. Совместная система называется определенной, если она
имеет только одно решение, и неопределенной в противном случае.
Определение 5. Две системы называются равносильными, если они
имеют одно и то же множество решений.
37.
В методе Гаусса 2 этапа.I этап (прямой ход): пользуясь теоремой Кронекера-Капелли, выяснить
совместность или несовместность системы, ее определенность или
неопределенность.
II этап (обратный ход): если система совместна, найти все решения
системы.
Теорема (Кронекера-Капелли). Для того чтобы система (1) была
совместной, необходимо и достаточно, чтобы ранг матрицы A был равен
рангу расширенной матрицы A : rang A rang A
38.
При этом будем различать случаи:1. система имеет единственное решение, если rang A rang A п;
2. система имеет бесчисленное множество решений, если
rang A rang A п;
3. система не имеет решений, если rang A rang A .
Здесь п - число неизвестных системы.
39.
Контрольные вопросы и задания3 4 3 1 4
1. Вычислить определители:
, 2 2 5 .
2 5
3
6
1
2. Можно ли сказать, чему равны определители, не вычисляя их:
а)
2 3 5
1 4 1
0
0
0
б)
4 2 2
6 3
3
1 4 4
в)
4 6 2
5 0 3 . Поясните ответ.
2 3 1
5 4 2
3. В силу какого свойства определитель 2 1 7 равен нулю?
3 3 5
4. Даны матрицы А 6 1 2
1 5 3 . Найти матрицу С= 2А-3В.
В
2
1
4
4
3
2
5. Пусть
3 4
2
4
1
В 1 5 . Можно ли умножить матрицу В на
А
1 2 5
2 0
матрицу А. Если да, найдите матрицe D=ВА.
40.
6.Возможно
ли,
найти
обратные
матрицы
для
матриц:
5 1
3 2
В 2 4 ? Ответ поясните.
А
6
4
0
3
2 1 5
7. Чему равен ранг матрицы: А 0 0 0 ?
0 4 3
8. Запишите формулы Крамера для системы двух уравнений с двумя
неизвестными.
9. Как записывается решение системы при решении ее матричным
способом?
10. Сколько решений имеет система, если выполнено условие:
rang A rang A п ?
11. Какая система уравнений называется определенной?
12. Какая система уравнений называется совместной?
13. Какая система уравнений называется однородной?
41.
Список рекомендуемой литературы1. Мустафина Л.М. Высшая математика для студентов технических
специальностей. Часть 1: Элементы линейной алгебры и аналитической
геометрии. Изд-во КарГТУ, Караганда, 2016.
2. Мустафина Л.М., Яруллина А.Р. Индивидуальные задания по высшей
математике для самостоятельной работы студентов технических
специальностей. Часть 1 (Определители. Матрицы. Системы линейных
уравнений. Элементы векторного анализа. Элементы аналитической
геометрии). Изд-во КарТУ, Караганда, 2021.




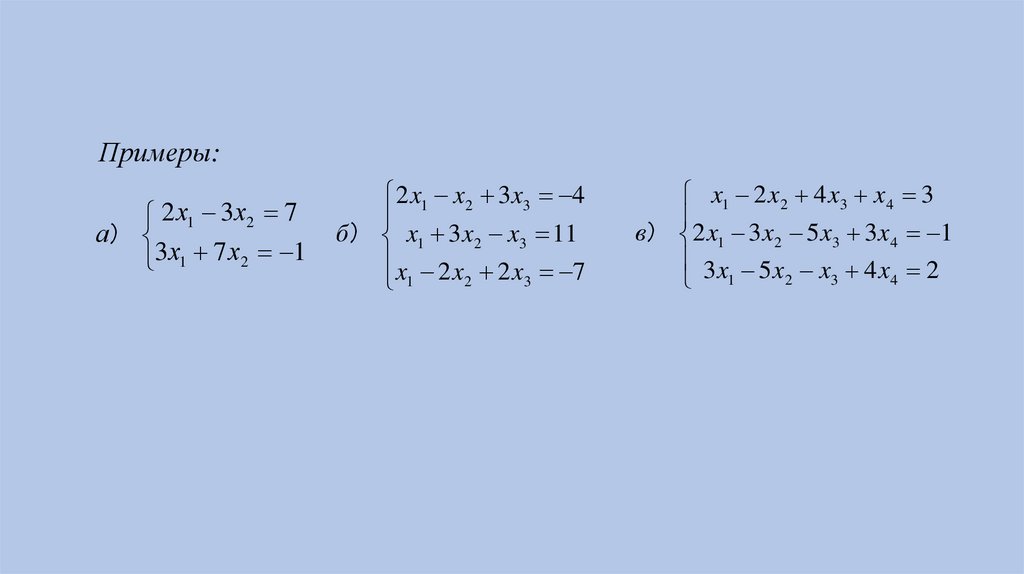






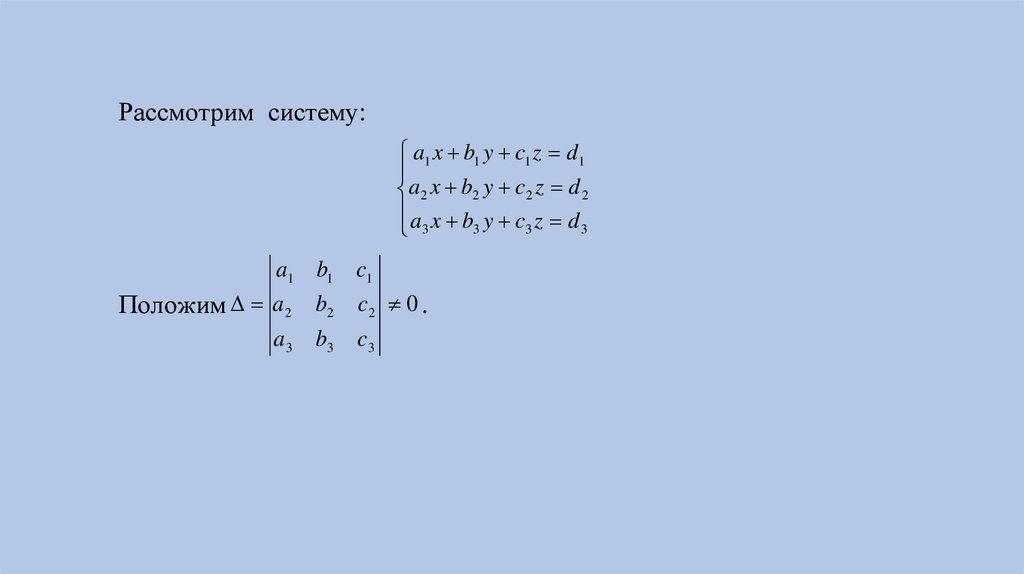





























 mathematics
mathematics








