Similar presentations:
Контактные явления. Контакт металл - полупроводник
1. Контактные явления
Часть I.Контакт металл-полупроводник
2.
Контакт металл-полупроводник (n-тип для наглядности)При возникновении контакта металл и полупроводник начинают обмениваться
электронами. Вначале поток из металла в полупроводник отличается от потока из
полупроводника в металл. Происходит перераспределение заряда такое, чтобы
возникшее электрическое поле выравнивало эти потоки. Вблизи контакта
возникает барьер для электронов из полупроводника (если изначально поток из
полупроводника больше) или металла (если изначала поток из металла больше),
а концентрация электронов в приконтактном слое может сильно отличаться от
концентрации в глубине полупроводника и металла. В металле избыточный заряд
“высаживается” на его поверхности = > весь переходной слой находится в
полупроводнике.
Надо выяснить, чем определяется барьер?
3.
dk1
H (r, k ) (k ) e (r )
3
H
(
r
,
k
)
F
2 exp
T
dk
1
dk
1
n(r )
2 3 exp (k ) F e (r) 2 3 exp (k )
T
T
F e электрохимический потенциал. Определяет ся концентрацией
n(r )
и температурой в данном месте полупроводника. Связь между и n такая
же как и при 0
В металле весь избыточный заряд выходит на поверхность. Внутри металла
практически ничего не меняется Весь контактный слой находится в п / п
(0) FM уровень Ферми в металле до приведения в контакт
( x d ) FП уровень Ферми в п / п до приведения в контакт
e (0) ( x d ) (0) ( x d ) FM FП
( x d ) const 0 начало отсчета
U (0) U K FП FМ
Высота барьера определяется разностью уровней Ферми полупроводника и
металла до приведения в контакт
4.
Чем определяется ширина барьера (ширина контакта)?D 4 ; e N d p N a n
D E
4
T d , a примеси полностью ионизованны N d nd ; N a na
Полупроводник n типа nd , n na , p e n0 n ; n0 nd na концентр.в глуб.п / п
4 e
n0 n
dk
1
2 3 exp (k ) F e 1
T
Невырожденный полупроводник
n
dk
F (k )
e
e
UK
n
exp
exp
n
exp
n
n
(
0
)
n
exp
0
K
0
3
T
T
T
T
2
4 en0
e
1 exp
T
Безразмерн ая потенциальная энергия
4 e 2 n0
1 exp
T
U
e
T
T
5.
D1
1 exp
2D
T
дебаевская длина экранирования определяет ширину контакта
4 e 2 n0
I )Обедненный слой запорный контакт 0
U К T Ф 1 exp 1
1
x
x
2 Ф
(
x
)
Ф
0
exp
U
(
x
)
U
exp
D
К
D
D
Ф 0
II )Сильно обедненный слой Ф 0, exp 1
1
x2
2 ( x) 2 C1 x C2
D
2 D
(d ) 0 C1
d
2D
d2
(d ) 0 C2 2
2 D
x2
d
d2
1
2
( x) 2 2 x 2 2 x d
2 D D
2 D 2 D
1/ 2
U
1
U
2
(0) K 2 d K d
2
T
2 D
T
2 e n0
6.
III )Обогощенный слой антизапорный контакт0; Ф 1 exp 1
1
exp
2D
dx
d ( )
2
1
dx exp
2
D
1
d exp
2D
2
exp C
2D
(d ) (d ) 0 C
2
D
2
2D
exp 1 1/ 2
0
2
D
exp 1 1/ 2
exp 1
2
D
exp / 2
7.
2D
exp / 2
1
exp
x C
2 D
UK
0 K
C exp К
T
exp K x
Ф x K 2 ln
1
2 D
nK
n( x) n0 exp
2
exp K x
1
2 D
8.
Вольт-амперная характеристика антизапорного (омического) контактаdn
j x e nE x eD dx
dE x 4
; e N d p N a n
dx
j x
t
x
Cттационарая ситуация
0 j x const
t
Примеси полностью ионизованны N d nd ; N a na ; n0 p0 nd na
Полупроводник n типа n0 , nd p0 , na n0 nd na
dn
D e
j
e
nE
eD
невырожденный полупроводник
x
x
dx
T
dE x 4 e n n
0
dx
9.
dnj
e
nE
T
(1)
dx
dE 4 e n n (2)
0
dx
dE
(2) n n0
(1)
4 e dx
d 2 E e dE 4 0 e
e 4
E
E
j 0; (3) 0 e n0
2
dx
T dx
T
T
Рассмотрим ситуацию когда током диффузии (перв.чл.в (3)) можно пренебр.
Когда это можно сделать ?
dx(3)
dE e 2
E const
dx 2T
Током диффузии можно пренебречь, если
dE
e
E 2
dx
T
d
d
E
u Edx прилож.напряж
dx
0
(d ) 0
u
Теорема о среднем u E d E
d
dE E
u
2
dx d d
dE
e 2
u
e u2
T
E 2
u
0.025 В при Т 300 К
dx
T
d
T d2
e
10.
dE 4 04
E
j 0
dx
Обезразмер иваем
E
dE 0
E
E 1 0
4 j dx
j
Безразмерн ая напряженно сть E1
0
j
E
0 E e n0 E
n
E1 0
j e nE
n
dE
jE1 1 E1 1 0
4 0 0
dx
М
максвеллов ское время релаксации
4 0
1
0 e n0 en0
М j dE1
en0
E1
dx
E1 1 0
Безразмерн ая координата
x1
en0
dE
x E1 1 E1 1 0
М j
dx1
11.
0n0
м j
dE1
E1
E1 1 0; E1
E ; x1
dx1
j
n
en0
Граничное условие E1 (0)
n0
1 обогащенный слой
nК
Общее решение
E1 ln 1 E1 x1 C
1
1
C E1 (0) ln 1 E1 (0) E1 (0) E1 (0) E12 (0) E12 (0)
2
2
1 n
C 0
2 nК
2
1
12.
Падение напряжения на контактеd
u Edx x1
0
en0
x; E1 0 E
М j
j
j М j
u
E1dx1
0 en0 0
d
d
u1 E1dx1 ; u1
0
en0 0
u
2
М j
Переходим к интегрир. по E1
1 n
x1 ( E1 ) E1 ln 1 E1 C ; C 0
2 nК
dx1 dE1
d
2
1
dE1
E dE
1 1
1 E1
1 E1
E1 ( d )
E12 dE1
u1 E1dx1
dx1
1
E
1
0
E1 ( 0 ) 1
E1 ( d )
0
( E12 1 1)dE1
1
dx1 E12 (d ) E1 (d ) ln 1 E1 (d )
1 E1
2
13.
1 21 n0
u1 E1 (d ) E1 (d ) ln 1 E1 (d ) E1 (d ) ln 1 E1 (d ) x1
2
2 nK
2
1
1 n
u1 E12 (d ) x1 (d ) 0 (1)
2
2 nK
1 n0
E1 (d ) ln 1 E1 (d ) x1 (d )
2 nK
j (u )
2
(2)
2
14.
1 n0E1 ( x1 ) ln 1 E1 ( x1 ) x1
2 nK
I ) Слабые токи
2
en0
x1
x 1
М j
n0
n0
1, E1 1 (2) ln 1 E1 ( x1 ) x1 0 j 0
nK
n
1 E1 ( x1 ) exp x1 1 E1 ( x1 ) 1 E
d
u Edx
0
j
0
d j
0
d
u закон Ома
j
0
15.
1 nE1 ( x1 ) ln 1 E1 ( x1 ) x1 C ; C 0
2 nK
II ) Сильные токи
E1
0
j
2
E 1
1
ln 1 E1 E1 E12 (d )
2
1
E12 x1 C
2
1
II .a ) x1 C E12 x1 0 j 0
2
1/ 2
2j
E1 2 x1 E
M 0
1/ 2
8 jd 3
u Edx
9 M 0
0
d
x1/ 2
j
9
2
u
закон Мотта
M
0
3
8d
1
1 n
II .б ) x1 C E12 C 0
2
2 nK
d
u Edx
0
2
n
E1 0 E 0
j
nK
jn0 d
e nK
j
u закон Ома
0 nК
d
16.
Диодная теория запорного контактаd
d
Ex
u dxExв неш
dx
0
(d ) 0
Контактный слой обеднен носителями =>
обладает большим сопротивлением =>
практически вся разность потенциалов
приходится на контактный слой
Длина свободного пробега>>толщины контакта => в металл проходят все
электроны полупроволника, движущиеся против оси х (px<0) и достигшие
контакта (плоскости x=d) с кинетической энергией движения вдоль оси х,
большей высоты барьера
p x2
U к eu
p x 2m U к eu
2m
px 0
17.
Вклад в ток с импульсами от p до p+dpp
dj xп м e x dn(p)
m
Контактный слой обеднен носителями => обладает большим сопротивлением =>
практически вся разность потенциалов приходится на контактный слой => за
пределами контактного слоя можно использовать распределение Максвелла
(полупроводник невырожденный)
p2
n0
dp n 0 dn(p) A
dn(p) A exp
3/ 2
2
mT
2
mT
dj
п м
x
p2
en0
dp
p x exp
3/ 2
m 2 mT
2mT
Ток из п / п в металл
j
п м
x
en0
3/ 2
m 2 mT
en0
3/ 2
m 2 mT
en0
3/ 2
m 2 mT
2 m U к eu
p x2 p y2 p z2
dpx dp y dpz px exp 2mT
p y2
p x2
p z2
dpx px exp 2mT dp y exp 2mT dpz exp 2mT
2 m U к eu
1
2
2
2mT dx exp x dy exp y
2
U к eu / T
2
18.
jп м
x
2
en0
1
2
2
2mT dy exp y dx exp x
3/ 2
m 2 mT 2
U к eu / T
1/ 2
j xп м
1 8T
U
eu
e
n0 exp k exp
4 m
T
T
eu
j xп м (u ) j 0 exp
T
1/ 2
1
Uk
8T
j0 j xп м (u 0) e vT nk ; vT
;
n
n
exp
k
0
4
m
T
При u 0 : j xм п (u 0) j xп м (u 0) j0
Для электронов со стороны металла барьер отсутствует j xм п (u ) j xм п (u 0)
Полный ток из полупроводника в металл
eu
j x (u ) j 0 exp 1
T
j x j xп м j xм п
19.
du dxExвнеш 0
0
d
u dxExвнеш 0
0
d
u dxExвнеш 0
0
d
u dxExвнеш 0
0
eu
j x (u ) j 0 exp 1
T
20.
Диффузионная теория запорного контактаДлина свободного пробега меньше или порядка ширины запорного слоя
dn
j
e
nE
eD
x
x
dx
2
4
d
; e N d p N a n
2
dx
j x
t
x
0 j x const
t
Примеси полностью ионизованны N d nd ; N a na ; n0 p0 nd na
Cттационарая ситуация
Полупроводник n типа n0 , nd p0 , na n0 nd na
dn
d D e
j x e nE x eD dx E x dx ; T невырожденный полупроводник
2
d 4 e n n
0
dx 2
21.
ddn
j x e n dx T dx (1)
2
d 4 e n n (2)
0
dx 2
Граничные условия
d
x d : 0;
0; n n0 (3)
dx
UK
x 0 : K u
u (4)
e
Алгоритм решения задачи
(1) (2) n ( x), j (2) ( x, j ) (4) j (u )
22.
ddn
T
dx
dx
dn e d
j
n
dx T dx
T
j e n
e
Обшее однородного j 0 no ,o C exp
T
Частное неоднородного j 0
e
Попробуем убрать второе слагаемое. Ищем решение в виде nч ,н ( x) exp f ( x)
T
e d
j
e df ( x) e d
n exp
n
T dx
T dx
T
T dx
df ( x)
j
j
e ( x)
e ( x)
e ( )
exp
exp
nч ,н ( x)
d exp
dx
T
T
T
T
T
0
x
j
e ( x)
e ( x)
e ( )
Общее неоднородного n( x) C exp
exp
d
exp
T
T T
T 0
x
j
e ( )
Граничные условия n(d ) n0 ; ( x) 0 C n0
d
exp
T 0
T
d
d
x
j
e ( x)
e ( x)
e ( )
e ( )
n( x) n0 exp
exp
d exp
d exp
T
T
T
T
T
0
0
23.
dj
e ( x)
e ( )
n( x) exp
d exp
n0
T x
T
T
d 2 4 e
n n0
Подставляем в уравнение Пуассона 2
dx
d
d 2 4 e
e
(
x
)
j
e
(
)
exp
d exp
2
n0
n0
T
T x
T
dx
UK
(
0
)
u
j (u )
e
d
dx (d ) (d ) 0
Интегро-дифференциальное уравнение. В общем случае нельзя решить
аналитически. Нужен численный расчет.
24.
j j п м j м пЭлектроны полупровод. достигшие границы контакта не испыт.
сопротив. и свободно проходят в металл
1
j п м (u ) e vT n(0, u )
4
1
Для электронов в металле барьера нет j м п (u ) j м п (u 0) e vT nК
4
1
j e vT n(0, u ) nК
4
U
Часто j j п м , j м п n(0, u ) nК n0 exp K
T
25.
je ( x)
e
n( x) n0 exp
d exp ( x) ( )
T T x
T
Граничное условие на плоскости контакта
d
UK
UK
( 0)
u; n(0) nk n0 exp
e
T
U
nK n0 exp K
T
j
eu
e
exp
d
exp
(
0
)
(
)
T T 0
T
d
eu
j j0 exp 1 диодная ВАХ
T
TnK
j0 d
e
0 d exp T (0) ( )
26.
j0TnK
e
d
exp
(
0
)
(
)
0
T
(0) ( ) 0 основной вклад в интеграл 0
d
d
( ) (0)
(0) E (0) (0) E (0)
dx 0
T
e
0 d exp T E (0) e E (0)
d
e
1 exp T E (0) d
e nk E (0)
j0
e
1 exp E (0) d
T
T e E (0) d j0 e nk E (0)






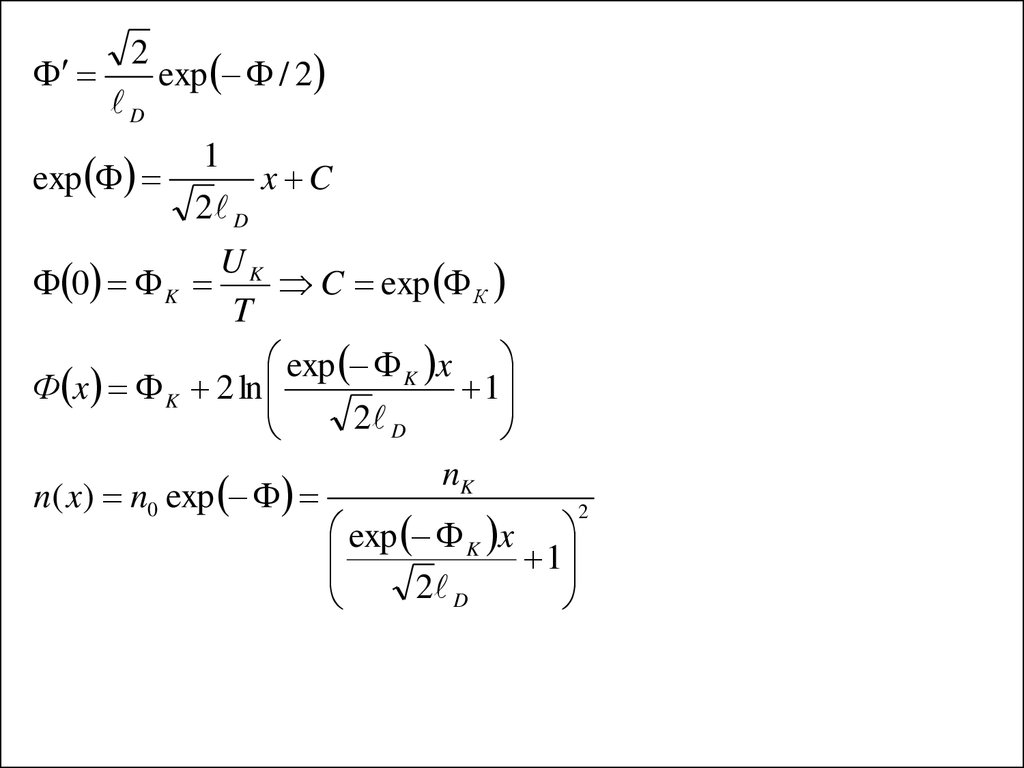





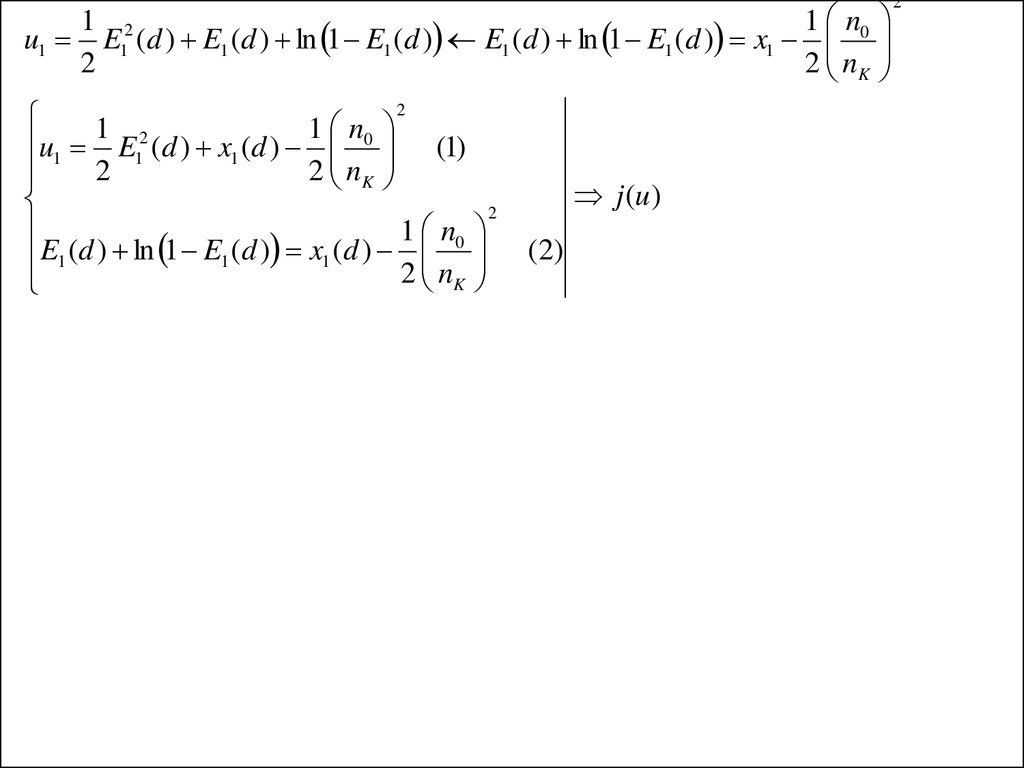













 physics
physics








