Similar presentations:
Статистика электронов и дырок в полупроводниках в условиях термодинамического равновесия
1.
Курс лекцийФизика полупроводников и
полупроводниковых приборов
СТАТИСТИКА ЭЛЕКТРОНОВ И ДЫРОК В ПОЛУПРОВОДНИКАХ В
УСЛОВИЯХ ТЕРМОДИНАМИЧЕСКОГО РАВНОВЕСИЯ
1
2.
ГЛАВА 2. СТАТИСТИКА ЭЛЕКТРОНОВ ИДЫРОК В ПОЛУПРОВОДНИКАХ В УСЛОВИЯХ
ТЕРМОДИНАМИЧЕСКОГО РАВНОВЕСИЯ
,
2.1. Плотность квантовых состояний
Энергетический спектр электронов количественно
можно описать "плотностью состояний".
Плотность состояний – это число состояний в
единичном интервале энергий для единичного объема
кристалла.
dN
N(E)=
dE
dN ( E ) N ( E )dE
d
2
3.
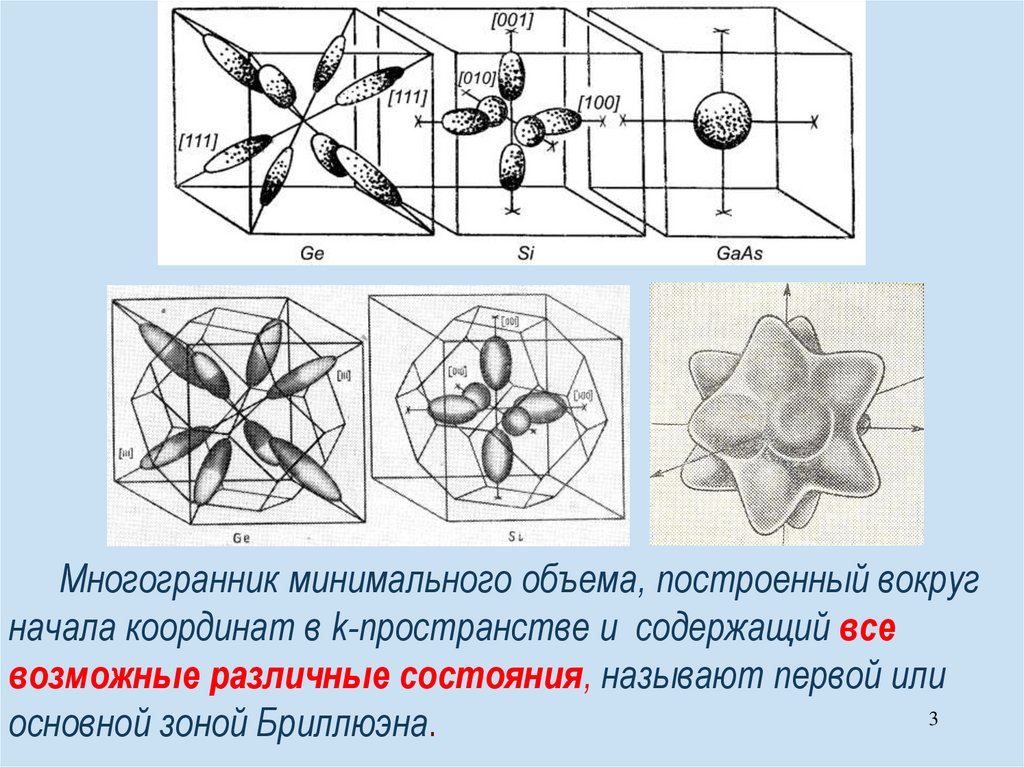
Многогранник минимального объема, построенный вокругначала координат в k-пространстве и содержащий все
возможные различные состояния, называют первой или
3
основной зоной Бриллюэна.
4.
dN ( E ) N ( E )dEd
1. Изоэнергетические поверхности имеют форму
сферы с минимальной энергией Emin в центре
зоны Бриллюэна
2
d 4 p dp
4
5.
dN ( E ) N ( E )dEd
1. Изоэнергетические поверхности имеют форму
сферы с минимальной энергией Emin в центре
зоны Бриллюэна
2
d 4 p dp
p2
E (k ) Ec
*
2m n
p 2 2mn* ( E Ec ); p (2mn* )1 / 2 ( E E c )1 / 2
d 4 p dp 2 (2m ) ( E Ec ) dE
2
* 3/ 2
n
1/ 2
5
6.
67.
dN ( E ) N ( E )dEd
1. Изоэнергетические поверхности имеют форму
сферы с минимальной энергией Emin в центре
зоны Бриллюэна
2
d 4 p dp
p2
E (k ) Ec
*
2m n
p 2 2mn* ( E Ec ); p (2mn* )1 / 2 ( E E c )1 / 2
d 4 p dp 2 (2m ) ( E Ec ) dE
2
* 3/ 2
n
2m
dN N ( E )dE 2 2
h
*
n
2m
N ( E ) 4 2
h
*
n
1/ 2
3/ 2
( E Ec )1 / 2 dE
3/ 2
( E E c )1 / 2
7
8.
Случай М сферических поверхностей,расположенных на расстоянии p0 от
центра зоны Брюллеэна.
*
2m n 3 / 2
N ( E ) M 4 ( 2 ) ( E E c )1 / 2
h
8
9.
Случай M эллипсоидальных изоэнергетических поверхностей2
x
p
2
y
2
z
p
p
E (k ) Ec
2m1 2m2 2m3
Где m1, m2 и m3 – компоненты
тензора эффективной массы
Уравнение эллипсоида в канонической форме
где полуоси эллипсоида:
p2
p2
p2
x
2
1
a
2
y
a2
a
z
2
3
1
ai [ 2 mi ( E Ec )]
1/ 2
Объем эллипсоида с полуосями а1, a2, a3 равен:
4
4
a1 a 2 a3
(8m1 m2 m3 )1 / 2 ( E E c ) 3 / 2 , а тонкого слоя:
3
3
dГ 2 (8m1 m2 m3 )
1/ 2
( E Ec )
1/ 2
dE
9
10.
учитывая, что минимумов энергии может быть М, получим:dГ M 2
1/ 2
1/ 2
dN M 3
(
8
m
m
m
)
(
E
E
)
dE
1 2 3
c
3
h
h
Если введем понятие эффективной массы плотности
квантовых состояний для электронов :
*3
n d
m
M (m1m2 m3 )
2
*
Тогда:
2m n d 3 / 2
1/ 2
N ( E ) 4 ( 2 ) ( E Ec )
h
эллипсоидальную поверхность равной энергии зоны
проводимости можно заменить сферой, если ввести
эфф. массу плотности состояний для электронов
10
11.
2.2. Функции распределения частиц. Функция Ферми-ДиракаФункцией распределения в стат. теории называют функцию, которая
в условиях термодинамического равновесия при заданной Т пропорциональна вероятности того, что некоторая частица занимает
определенный энергетический уровень Е.
11
12.
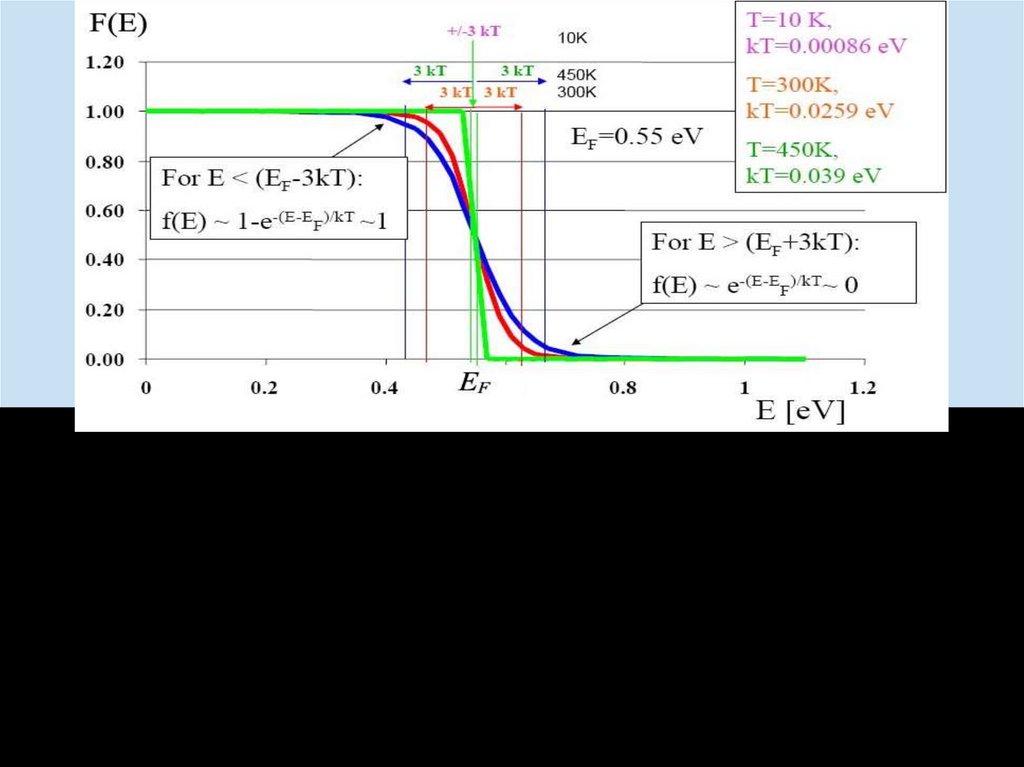
2.2. Функции распределения частиц. Функция Ферми-Дирака1
F (E)
e
E EF
kT
1
1. E EF F ( E) 0,5
2. T 0
3. E E
E EF
F (E) 1
E EF
F (E) 0
F kT
4. E F E kT
5.
E E F
F ( E ) exp
kT
E EF
F ( E ) 1 exp
kT
12
13.
1314.
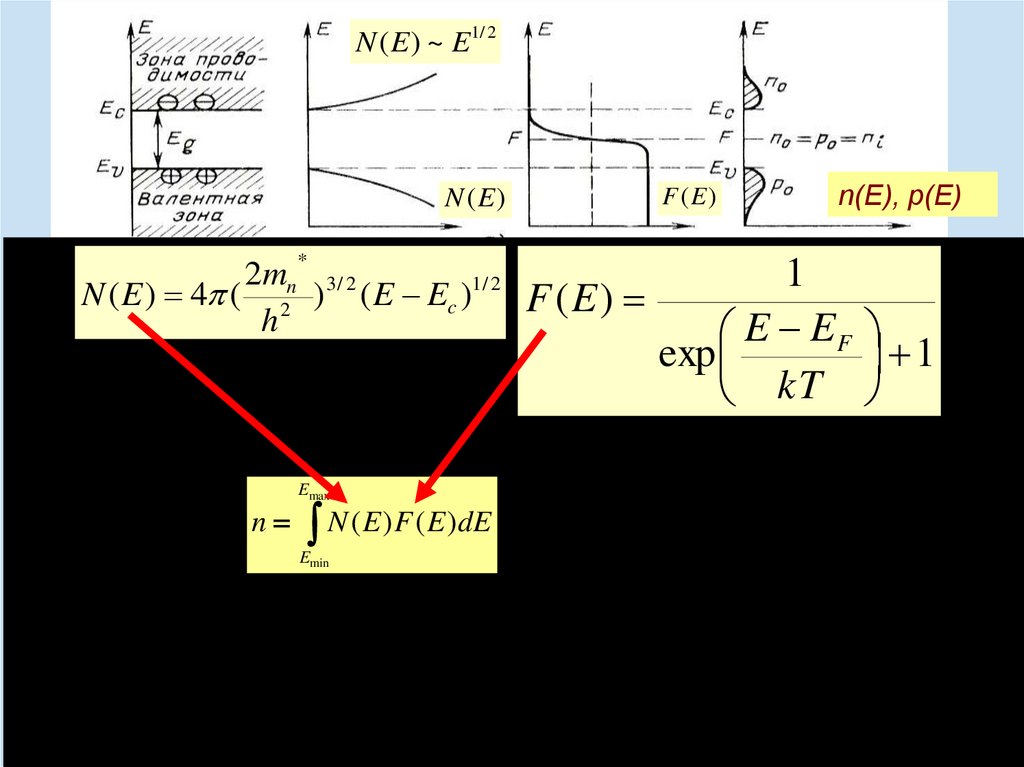
N ( E ) ~ E1/ 2N (E )
*
2m
N ( E ) 4 ( 2n )3 / 2 ( E Ec )1/ 2
h
F (E )
n(E), p(E)
1
F (E)
E EF
exp
1
kT
Emax
n N ( E ) F ( E )dE
Emin
14
15.
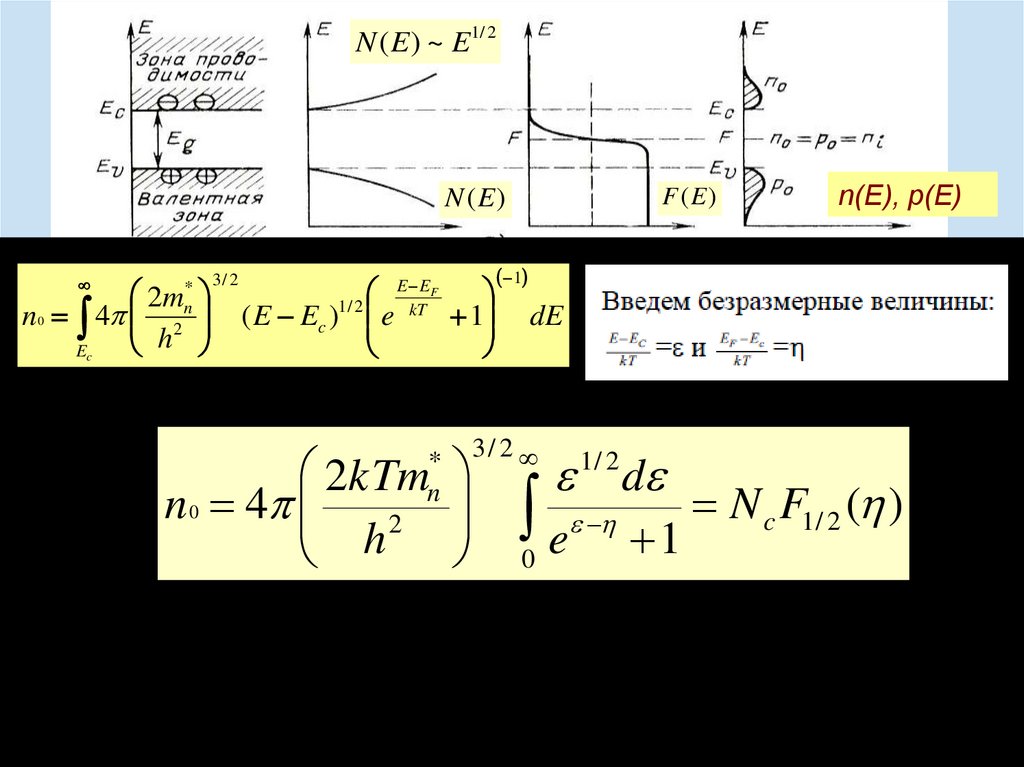
N ( E ) ~ E1/ 2F (E )
N (E )
3/ 2
2m
1/ 2
n0 4 2 ( E Ec ) e
h
Ec
*
n
E EF
kT
1
2kTm
n 0 4
2
h
*
n
n(E), p(E)
1
dE
3/ 2
d
1/ 2
e 1 N F ( )
c 1/ 2
0
15
16.
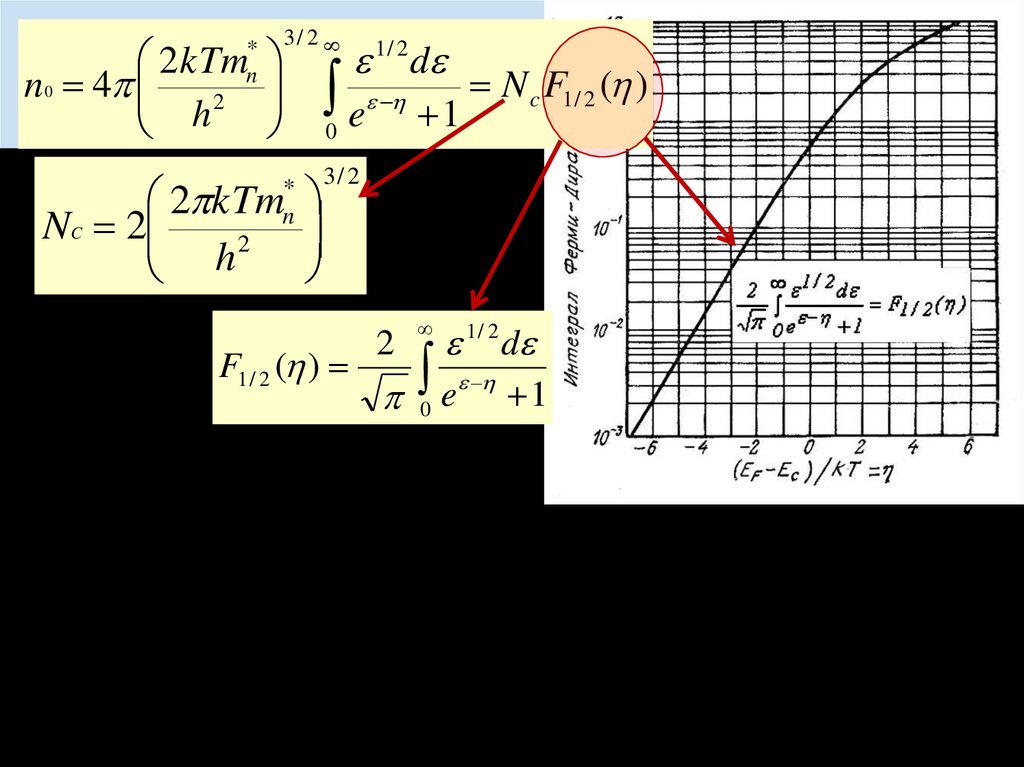
2kTmn 0 4
2
h
*
n
3/ 2
2 kTm
NC 2
2
h
*
n
1 / 2 d
e 1 N F ( )
c 1/ 2
0
3/ 2
F1 / 2 ( )
2
1 / 2 d
0 e
1
16
17.
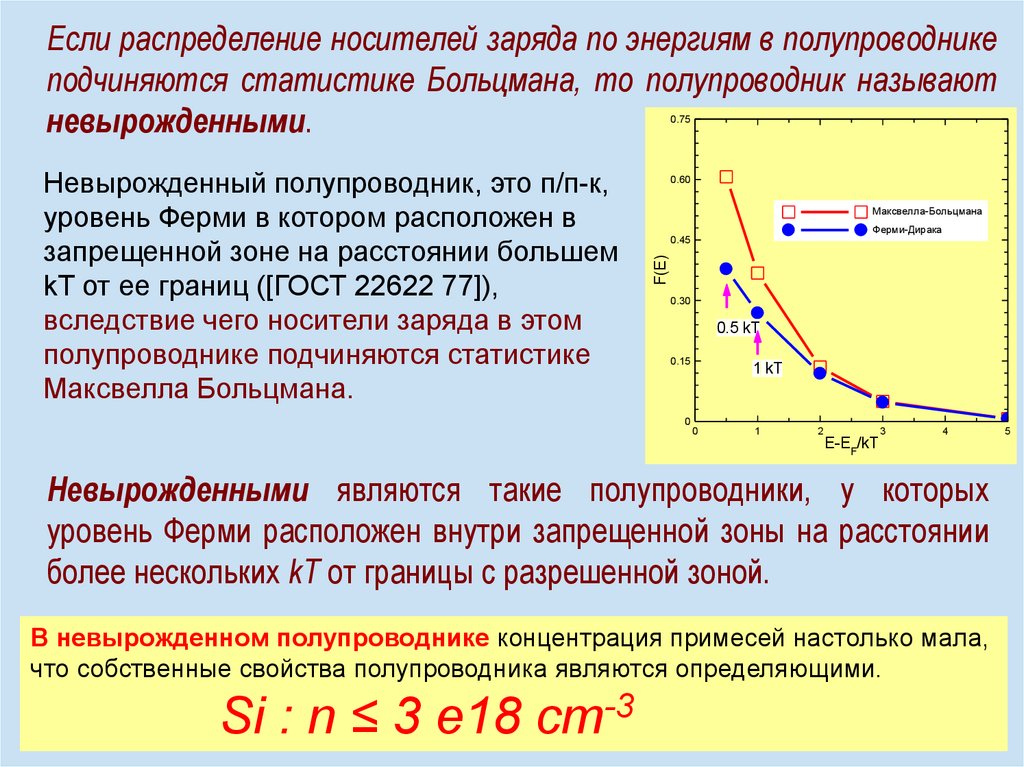
Если распределение носителей заряда по энергиям в полупроводникеподчиняются статистике Больцмана, то полупроводник называют
невырожденными.
0.75
0.60
Максвелла-Больцмана
Ферми-Дирака
0.45
F(E)
Невырожденный полупроводник, это п/п-к,
уровень Ферми в котором расположен в
запрещенной зоне на расстоянии большем
kT от ее границ ([ГОСТ 22622 77]),
вследствие чего носители заряда в этом
полупроводнике подчиняются статистике
Максвелла Больцмана.
0.30
0.5 kT
0.15
0
1 kT
0
1
2
E-EF/kT
3
4
Невырожденными являются такие полупроводники, у которых
уровень Ферми расположен внутри запрещенной зоны на расстоянии
более нескольких kT от границы с разрешенной зоной.
В невырожденном полупроводнике концентрация примесей настолько мала,
что собственные свойства полупроводника являются определяющими.
Si : n ≤ 3 e18 cm-3
17
5
18.
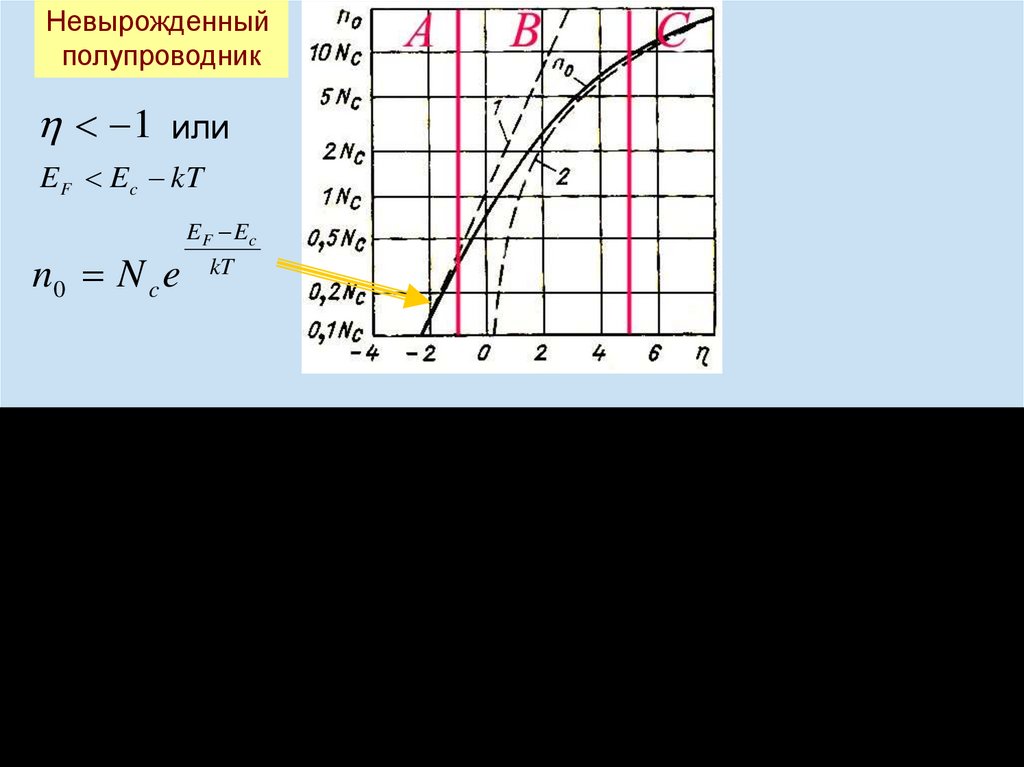
Невырожденныйполупроводник
1 или
E F Ec kT
n0 N c e
E F Ec
kT
18
19.
1920.
Полупроводники, у которых распределение свободныхНЗ по энергетическим состояниям описывается
функцией Ферми-Дирака, называются вырожденными.
Вырожденный полупроводник — это п/п-к, концентрация примесей в
котором настолько велика, что собственные свойства практически не
проявляются, но преобладают свойства примеси:
-У вырожденного полупроводника уровень Ферми лежит внутри
разрешённых зон или внутри запрещённой зоны на расстояниях не
более kT от границ разрешённых зон.
-Вырожденные полупроводники получают путём сильного легирования
собственных полупроводников.
Si : n ≥ 5 e18 cm-3
20
21.
Сильно-вырожденныйполупроводник
Невырожденный
1
полупроводник
n0 N c e
E F Ec
kT
5 или
E F Ec 5kT
8 2m
2
n0
3 h
*
n
3/ 2
( E F0 Ec ) 3 / 2
21
22.
Невырожденныйполупроводник
n0 N c e
E F Ec
kT
Сильно-вырожденный
полупроводник
8 2mn*
2
n0
3 h
3/ 2
( E F0 Ec ) 3 / 2
Вырожденный
полупроводник
-1<η<5
NC
n0
0.17 e
22
23.
n0 N c eE F Ec
kT
p0 N V e
EV E F
kT
2 kTm
N C 2
2
h
*
n
3/ 2
2 kTm
NV 2
h2
*
p
3/ 2
2.5. Собственные и примесные полупроводники
2.5.1. Закон действующих масс (основное уравнение полупроводника)
23
24.
2.5.1. Закон действующих масс (основное уравнение полупроводника)Eg
n0 p0 ni pi const AT exp
kT
2
2
3
Произведение концентраций основных и неосновных
носителей заряда в невырожденном полупроводнике при
фиксированной температуре является постоянной
величиной, которая не зависит от концентрации
введенной примеси и равна квадрату концентраций
собственных носителей заряда при той же температуре.
24
25.
2.5. Собственные и примесные полупроводники2.5.2. Собственный полупроводник: концентрация носителей
заряда и положение уровня Ферми
2 k
ni 2 2
h
Eg
3/ 2
*
n
* 3/ 4
p
(m m ) T
3/ 2
e
Как определить ширину
запрещенной зоны?
Построение Аррениуса!
25
2 kT
26.
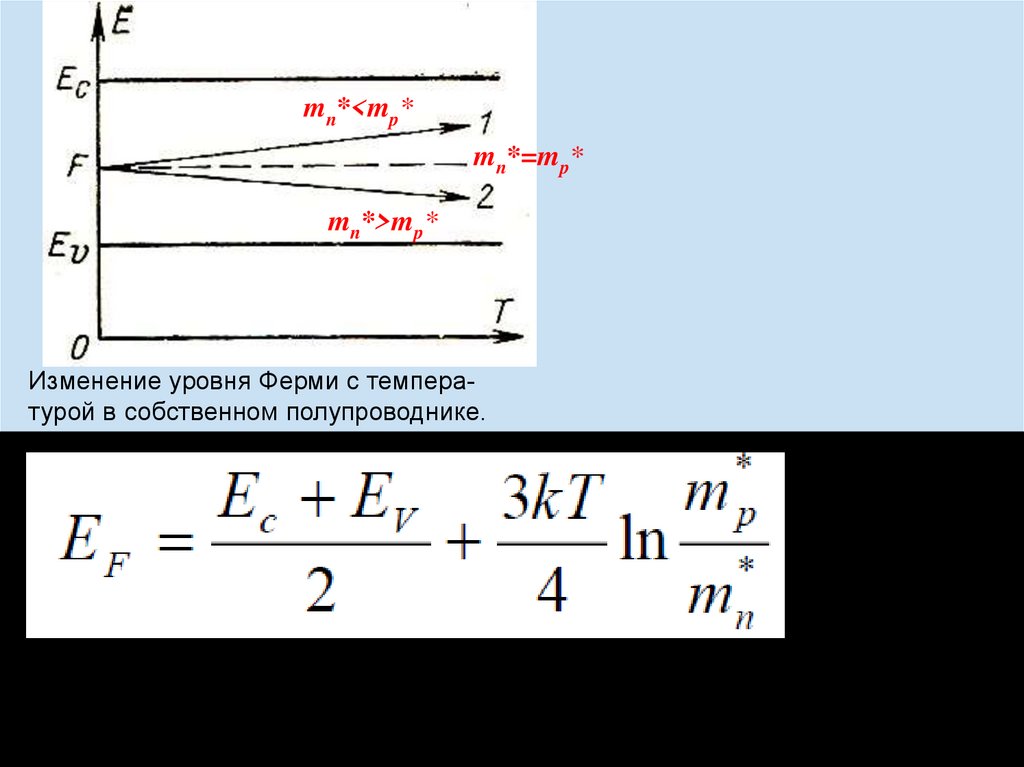
Положение уровня Ферми в собственном полупроводнике26
27.
mn*<mp*mn*=mp*
mn*>mp*
Изменение уровня Ферми с температурой в собственном полупроводнике.
27
28.
2.6. Зависимость уровня Ферми от концентрациипримесей и температуры для невырожденного
полупроводника
Зависимость EFот концентрации.
Зависимость EFот температуры.
;
28
29.
Нужно решить уравнение общейэлектронейтральности
E
EC
Ed
n0
n0 N c e
E F Ec
kT
p0 N V e
EV E F
kT
Nd, nd, pd
Ea
EV
Na, na, pa
nd = ?
pd = ?
na = ?
pa = ?
p0
Nd – концентрация атомов донорной легирующей примеси
пd.- концентрация атомов донорной примеси в нейтральном
зарядовом состоянии = электроны на донорных уровнях.
pd.- концентрация атомов примеси в ионизованном состоянии
(положительный заряд) = электроны в зоне проводимости.
рd = Nd - nd
29
30.
pdnd
1
E F Ed
2 exp
kT
нейтральное состояние донорной примеси
имеет вдвое больший статистический вес по
сравнению с ионизованным состоянием!!!
30
31.
pdnd
1
рd = Nd - пd
E Ed
2 exp F
kT
N d nd
nd
1
E F Ed
2 exp
kT
Nd
Nd
nd
E F Ed
E F Ed
1
1 / 2 exp
1 g exp
1
kT
kT
рd = Nd - пd
Nd
pd
E F Ed
g exp
1
kT
31
32.
EEC
Ed
n0
Nd, nd, pd
Ea
EV
Na, na, pa
p0
n0 N c e
E F Ec
kT
p0 N V e
Nd
E Ed
g 1 exp F
1
kT
pd
Na
na
Ea E F
g exp
1
kT
pa
nd
EV E F
kT
Nd
E F Ed
g exp
1
kT
Na
E EF
g 1 exp a
1
kT
32
33.
Нужно решить уравнение общейэлектронейтральности
E
EC
Ed
n0
n0 N c e
E F Ec
kT
p0 N V e
EV E F
kT
Nd, nd, pd
Ea
EV
Na, na, pa
Nd(+) = p d
Nd
E F Ed
g exp
1
kT
Na(-) = na
Na
Ea E F
g exp
1
kT
p0
33
34.
EEC
Ed
n0
n
p
d
0
N ,n ,p
d
d
n0 N c e
E F Ec
kT
Nd
pd
E F Ed
g exp
1
kT
d
EV
Nc N d
n0
N c ge d n0
;
d
ge n0 Ncn0 NcNd 0
2
ax bx c 0
2
34
35.
ax bx c 02
n0
2N d
4 gN d d
1
e
NC
b b 4ac
x1, 2
2a
NC
EF EC kT ln
1
2 N d
2
NC
d NC
ge
Nd
2Nd
2
35
36.
n02N d
4 gN d d
1
e 1
NC
NC
EF EC kT ln
2 N d
Случай А. Низкая
температура (0-50К)
NC
N
ge d C
Nd
2Nd
2
4 gN d d
NC
d
e 1 e
Nc
2N d
36
37.
NEF EC kT ln C
2 N d
2N d
n0
1
4 gN d d
e 1
NC
4 gN d d
e 1
Nc
1
n0 g N C N d
e d
Ec E d
1/ 2
2 kT
e
2
NC
N
ge d C
Nd
2Nd
NC
2N d
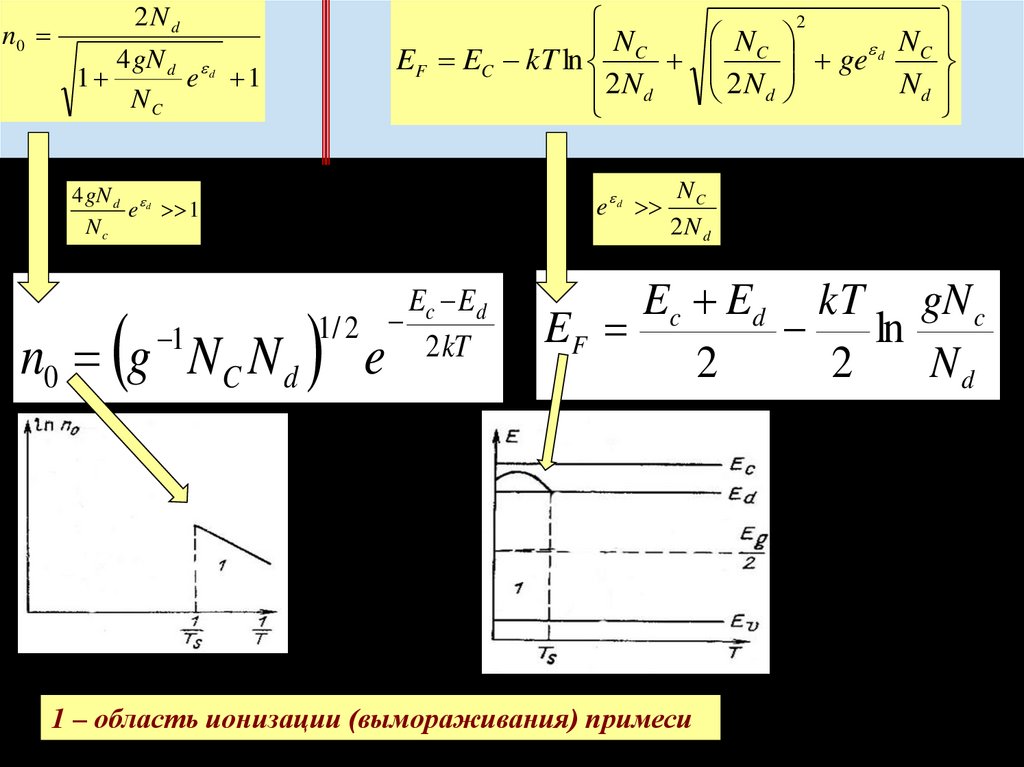
Ec Ed kT gN c
EF
ln
2
2
Nd
1 – область ионизации (вымораживания) примеси
37
38.
n02N d
4 gN d d
1
e 1
NC
NC
EF EC kT ln
2 N d
Случай Б. Средняя
температура (50К – 200С)
NC
N
ge d C
Nd
2Nd
2
NC
4 gN d d
d
e 1 e
2Nd
Nc
38
39.
2N dn0
1
4 gN d d
e 1
NC
N
EF EC kT ln C
2Nd
4 gN d d
e 1
Nc
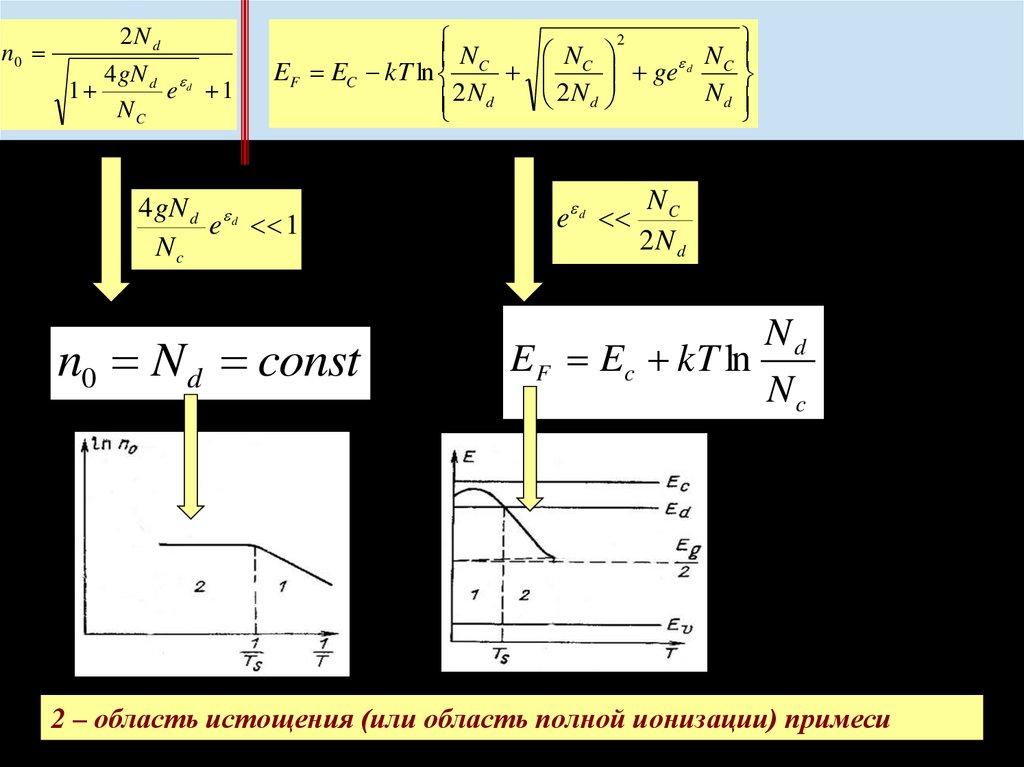
n0 N d const
2
NC
N
ge d C
Nd
2Nd
NC
e
2Nd
d
Nd
E F Ec kT ln
Nc
2 – область истощения (или область полной ионизации) примеси
39
40.
n02N d
4 gN d d
1
e 1
NC
NC
EF EC kT ln
2 N d
NC
N
ge d C
Nd
2Nd
2
Случай В. Высокая температура (>300 - 500 С)
40
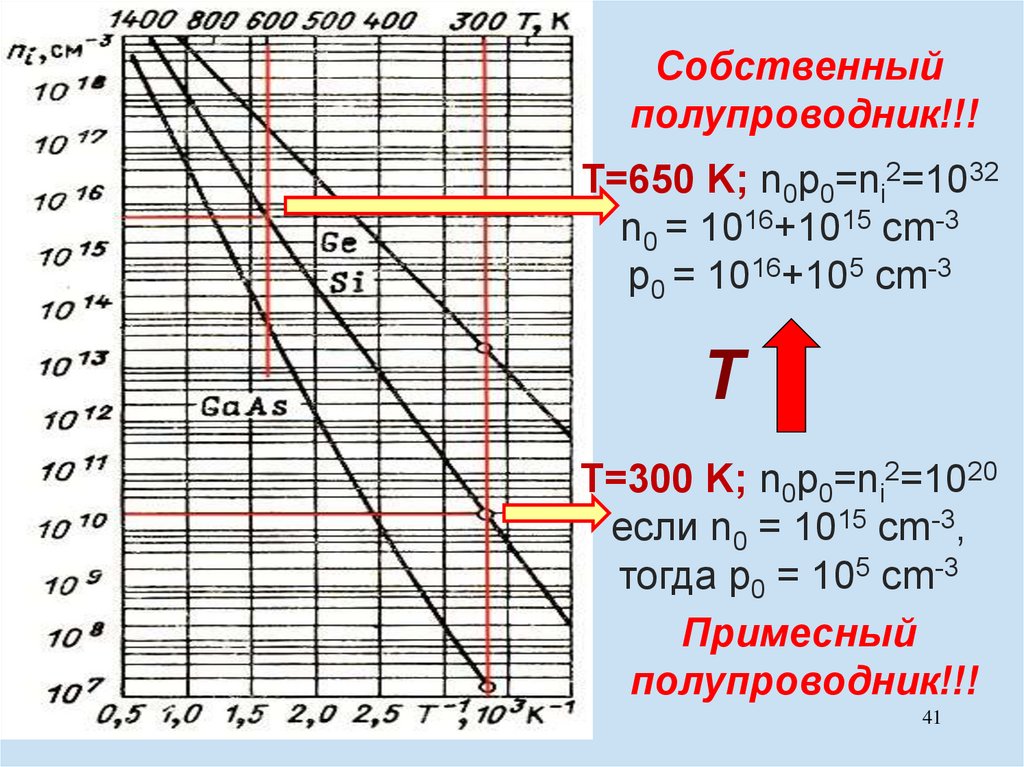
41.
Собственныйполупроводник!!!
T=650 K; n0p0=ni2=1032
n0 = 1016+1015 cm-3
p0 = 1016+105 cm-3
Т
T=300 K; n0p0=ni2=1020
если n0 = 1015 cm-3,
тогда p0 = 105 cm-3
Примесный
полупроводник!!!
41
42.
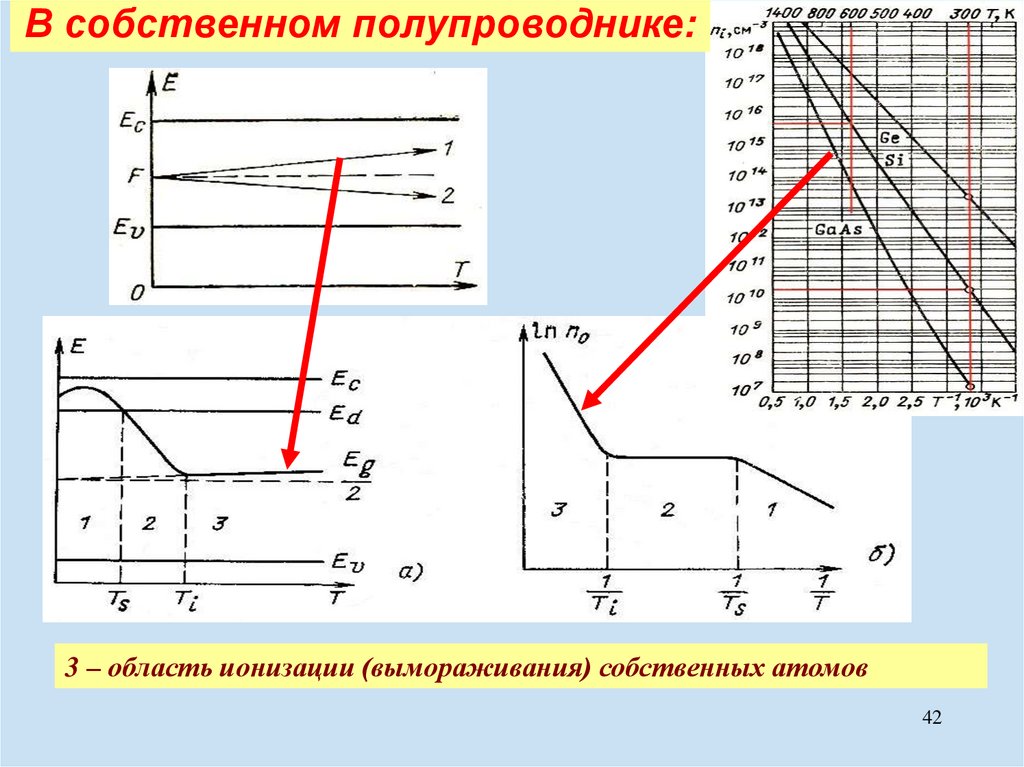
В собственном полупроводнике:3 – область ионизации (вымораживания) собственных атомов
42
43.
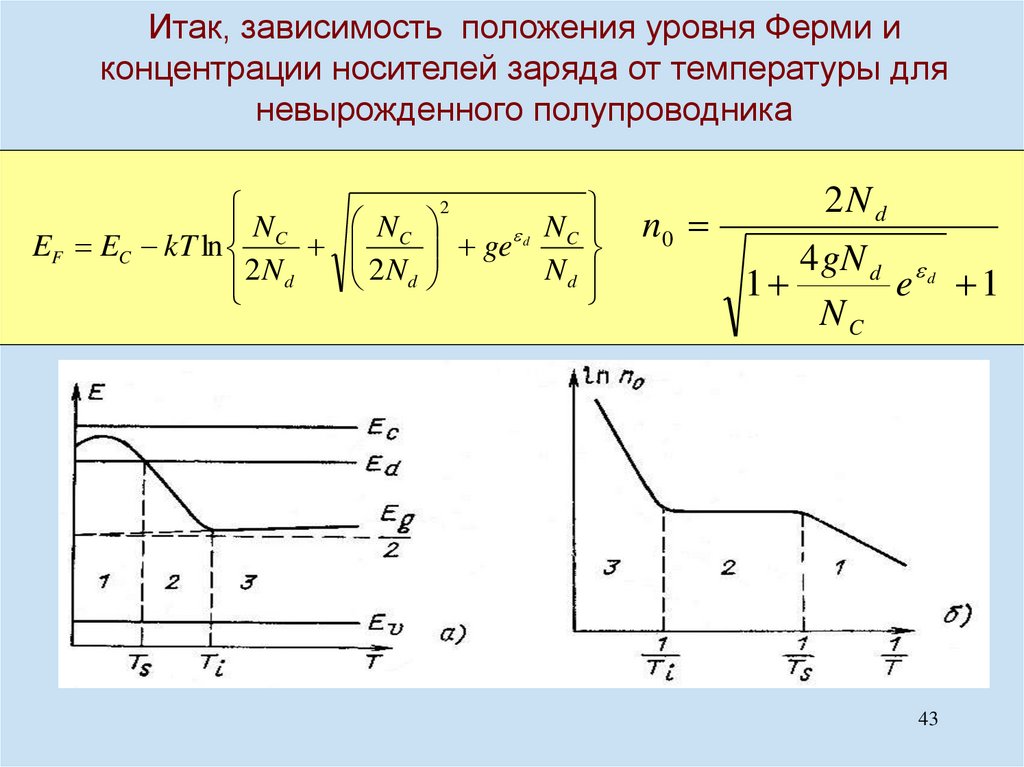
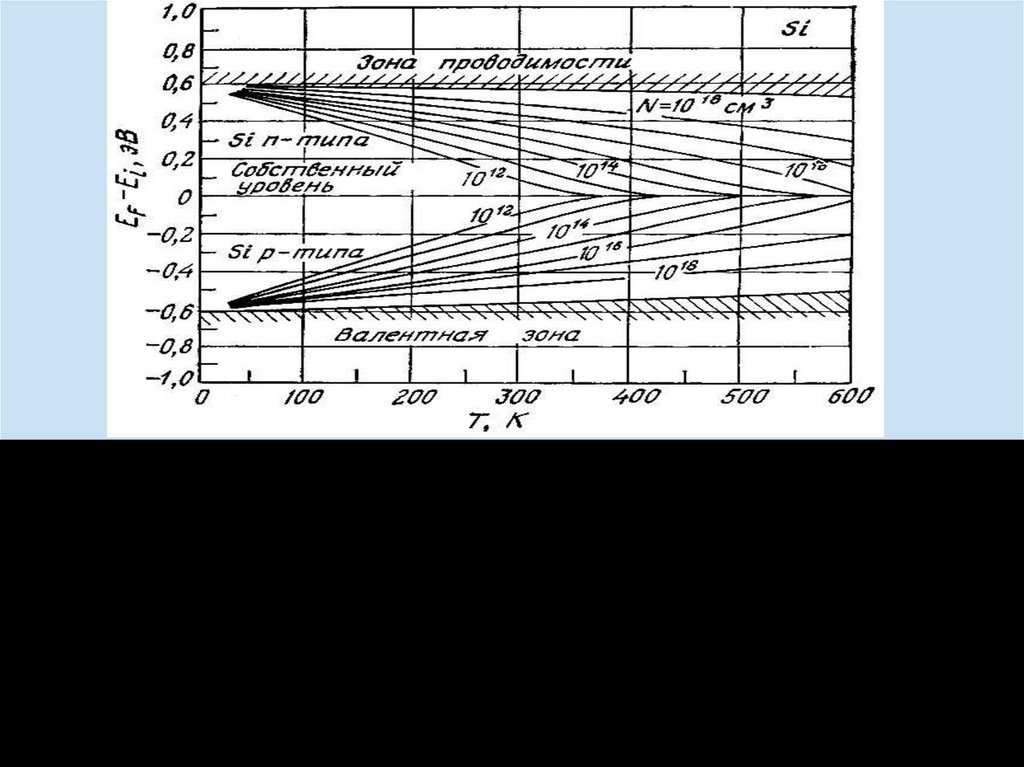
Итак, зависимость положения уровня Ферми иконцентрации носителей заряда от температуры для
невырожденного полупроводника
NC
EF EC kT ln
2 N d
NC
N
ge d C
Nd
2Nd
2
n0
2N d
4 gN d d
1
e 1
NC
43
44.
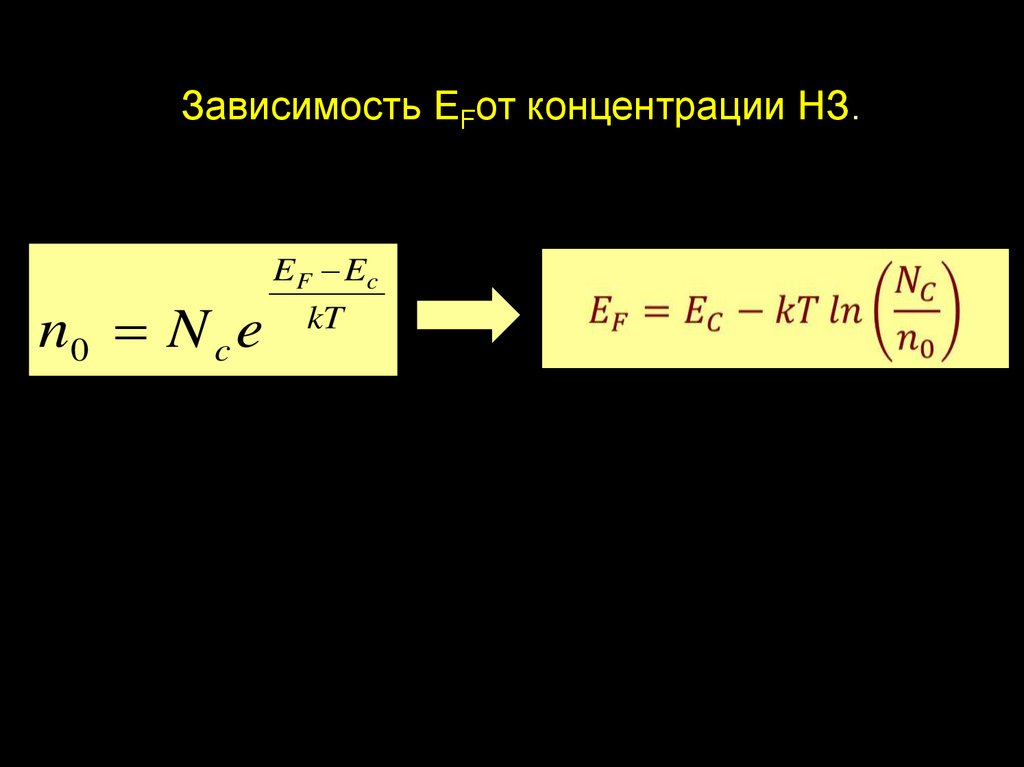
Зависимость EFот концентрации НЗ.n0 N c e
E F Ec
kT
;
44






























 physics
physics








