Similar presentations:
Оптимальное управление динамических систем. Гамильтониан и принцип максимума
1.
Оптимальное управлениединамических систем
Гамильтониан и принцип максимума
2.
Общие положенияH [x(t ), u(t ), t ] L[x(t ), u(t ), t ] λ T (t )f [x(t ), u(t ), t ]
H
0
u
H uu
(3.26)
(3.27)
2H
0
2
u
xˆ (t )
λˆ (t )
uˆ (t )
H[xˆ (t ), u(t ), λˆ , t ] H[xˆ (t ), uˆ (t ), λˆ , t ]
u(t )
(3.25)
[xˆ (t ), λˆ (t )]
uˆ (t )
(3.28)
3.
Уравнения Гамильтона-Якоби – Беллманаxˆ (t )
tf
J [x(tf ), tf ] L[x(t ), u(t ), t]dt
(3.29)
t0
x f (x, u, t )
uˆ (t )
x(t0 ) x 0
(3.30)
t0 t tf
tf
Vˆ[xˆ (t ), t ] [xˆ (tf ), tf ] L[xˆ ( ), uˆ ( ), ]d
(3.31)
t
t
Vˆ[xˆ (t ), t ] [xˆ (tf ), tf ] L[xˆ ( ), uˆ ( ), ]d
tf
(3.32)
4.
Уравнения Гамильтона-Якоби – БеллманаdVˆ
L[xˆ (t ), uˆ (t ), t]
dt
dVˆ Vˆ Vˆ
Vˆ Vˆ
x
f
dt
t
x
t
x
Vˆ
Vˆ
L[xˆ (t ), uˆ (t ), t]
f
t
x
Vˆ[xˆ (tf ), tf ] [xˆ (tf ), tf ]
x̂
t
x0
(3.33)
(3.34)
(3.35)
(3.36)
5.
,Уравнения Гамильтона-Якоби – Беллмана
Vˆ
H [xˆ (t ), λˆ (t ), uˆ (t ), t]
t
(3.37)
ˆ
ˆλ T V
x
u(t ) uˆ [t , x(t )]
(3.38)
(3.39)
x f (x, t )
x(t0 ) x 0
xe 0
Vˆ[xˆ (t ), t ]
Vˆ[xˆ (t ), t ]
V (x, t )
V (0, t ) 0
V (x, t ) 0
x ,V (x, t )
(3.42)
(3.40)
Vˆ[xˆ (t ), t ]
x 0
d
(x, t ) 0, x 0
dt
(3.41)
6.
Линейные зависящие от временисистемы с квадратичным показателем
качества
7.
x A(t )x(t ) B(t )u(t ), x(t0 ) x 0(3.43)
J xT (tf )Qf x(tf )
tf
[x (t )Q(t )x(t ) 2x (t )S(t )u(t ) u (t )R (t )u(t )]dt
T
T
(3.44)
T
t0
L[x(t ), u(t ), t] xT (t )Q(t )x(t ) 2xT (t )S(t )u(t ) uT (t )R(t )u(t )
(3.45)
8.
V [x(t ), t ]x(t )
P (t )
V [x(t ), t ] xT (t )P(t )x(t )
(3.46)
Vˆ[xˆ (tf ), tf ] xT (tf )Qf x(tf )
(3.47)
λT
V
2xT (t )P(t )
x
(3.48)
H xT (t )Q(t )x(t ) 2xT (t )S(t )u(t ) uT (t )R(t )u(t )
2x (t )P(t )[ A(t )x(t ) B(t )u(t )]
T
(3.49)
9.
Hu 0xˆ T (t )S(t ) uˆ T (t )R(t ) xˆ T (t )P(t )B(t ) 0
uˆ (t ) R 1 (t )[BT (t )Pˆ (t ) ST (t )]xˆ (t )
P (t )
V [x(t ), t ] 0
Vˆ
ˆ
H
xˆ T Pˆ xˆ
t
H uu 0
Pˆ (t )
R (t )
(3.50)
(3.51)
x(t )
(3.52)
ˆ
P(t )
V [x(t ), t ] 0, x(t ) E
10.
xˆ T Pˆ xˆ xˆ T [( A BR 1ST )T Pˆ Pˆ ( A BR 1ST )Pˆ BR 1BT Pˆ Q SR 1ST ]xˆ
(3.53)
Pˆ Q (A BR 1ST )T Pˆ Pˆ (A BR 1ST ) Pˆ BR 1BT Pˆ SR 1ST
Pˆ f Qf
Pˆ (t )
(3.55)
Qf , Q(t ), R(t )
(3.54)
11.
ЛекцияМетод АКОР
12.
t1 T
1 k T
J (u) x (t k ) k x (t k ) x (t ) x (t ) u T (t ) u(t ) dt
2
2 t0
x T (t ) x(t )
1 T
x (t k ) k x (t k )
2
u T (t ) u(t )
uопт (t ) 1BT (t ) K (t ) x(t ) D(t ) x(t );D(t ) 1BT (t ) K (t )
n
u j dij xi
i 1
13.
K (t ) K ( t ) A(t ) AT ( t ) K ( t ) K ( t ) B(t ) 1 BT ( t ) K ( t )x (t ) A(t ) B(t )D(t ) x(t ) Ao (t )x(t ); Ao (t ) A(t ) B(t )D(t )












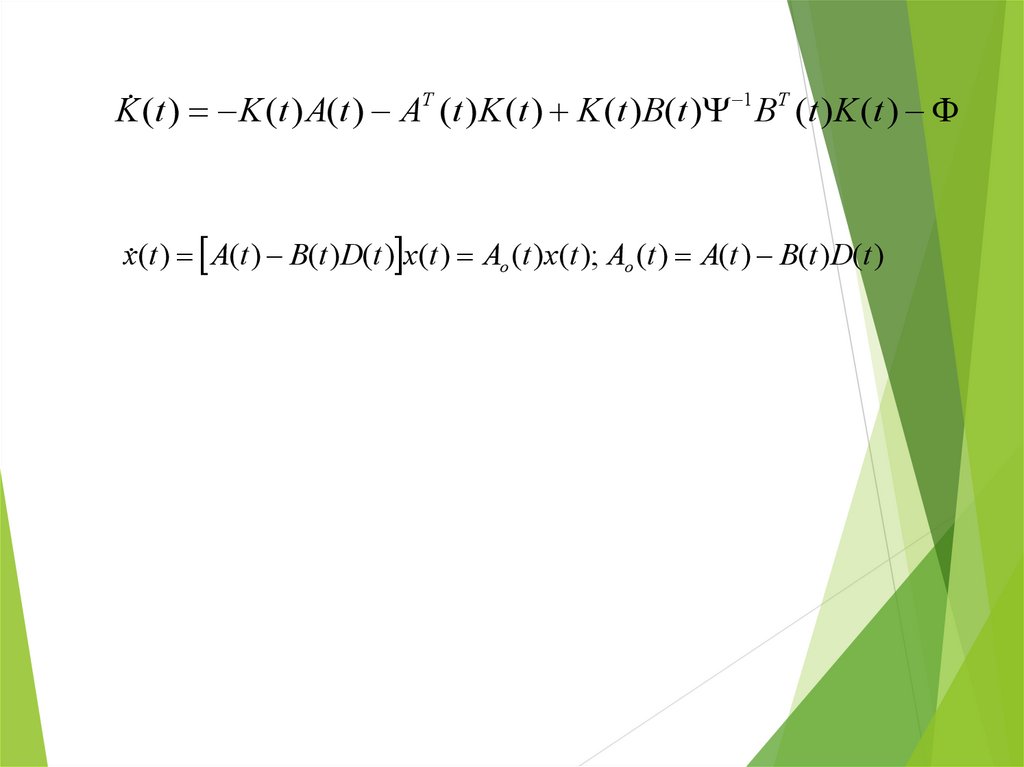
 mathematics
mathematics








