Стохастические динамические модели приборов и систем

1.

2.3. Стохастические динамические модели приборов и
систем

2.

2.3.2. Моделирование процедур оценивание параметров
состояния стохастических динамических систем в
непрерывном времени
Постановка задачи: для применения математического
аппарата оптимального оценивания в качестве
параметров состояния принимаются ошибки
стохастических динамических систем

3.

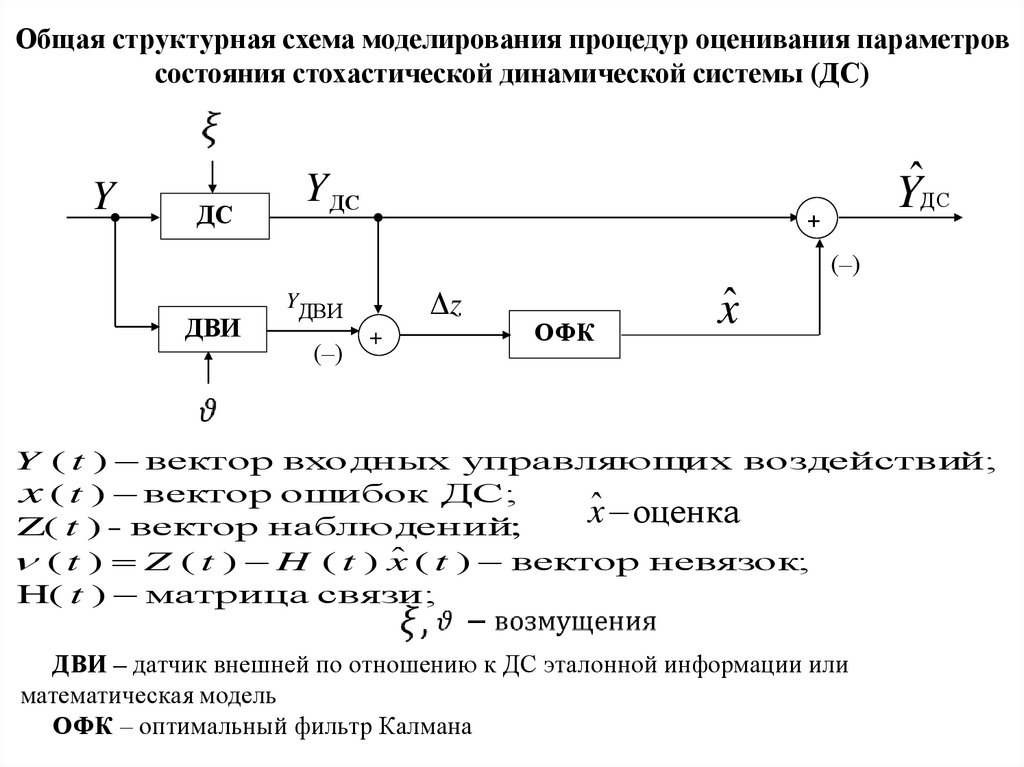
Общая структурная схема моделирования процедур оценивания параметров
состояния стохастической динамической системы (ДС)
Y
ДС
Y ДС
YˆДС
+
(–)
ДВИ
Δz
YДВИ
(–)
+
ОФК
x̂
Y ( t ) вектор входных управляющи х воздействий;
x ( t ) вектор ошибок ДС;
ˆ оценка
x
Z( t ) - вектор наблюдений;
ˆ ( t ) вектор невязок;
(t ) Z (t ) H (t ) x
H( t ) матрица связи;
ДВИ – датчик внешней по отношению к ДС эталонной информации или
математическая модель
ОФК – оптимальный фильтр Калмана

4.

Оптимальные оценки xˆ (t )
вектора ошибок x(t )
ДС могут быть найдены по
наблюдениям z (t ) . На практике в качестве критерия оптимальности принимают минимум
дисперсии ошибок оценивания. Вектор ошибок оценивания
e(t ) x(t ) xˆ (t )
характеризуется ковариационной матрицей
(2.27)
P(t ) M [e(t )eT (t )]
Диагональные элементы матрицы представляют собой дисперсии ошибок оценивания. С
учетом этого оптимальные оценки находятся из решения уравнения
(2.28)
xˆ (t ) arg min S P(t )
P
x (t )
n
где
S P P(t ) Pjj (t ) - след матрицы P(t ) , имеющий размерность n n ;
j 1
- j-й диагональный элемент матрицы P(t )
Для реализации критерия оптимальности (2.28) будем использовать структуру наблюдателя
состояния. Применительно к оценкам вектора ошибок уравнение наблюдателя примет вид
Pjj (t )
xˆ ( t ) A ( t ) xˆ ( t ) K ( t )[ z ( t ) zˆ ( t )]
(2.29)
где
– оптимальный коэффициент усиления, обеспечивающий выполнение
K (t )
условия (2.28; zˆ ( t ) H ( t ) xˆ ( t )] - прогноз наблюдения.
Для нахождения оптимального коэффициента усиления необходимо установить
взаимосвязь уравнений (2.28) и (2.29). Для этого определим выражение для производных
ковариационной матрицы и ошибок оценивания

5.

dP ( t )
d (t )
P ( t ) M [ e ( t ) e T ( t )] M [ e ( t ) e T ( t )]
(2.30)
de (t )
e (t ) x (t ) x ˆ (t ) A(t ) x(t ) G (t ) (t ) A(t ) xˆ (t ) K (t )[ z (t ) H (t ) xˆ (t )]
dt
A(t )[ х(t ) xˆ (t )] G (t ) (t ) K (t )[ H (t ) x(t ) (t ) H (t ) xˆ (t )]
A(t )e(t ) G (t ) (t ) K (t )[ H (t )e(t ) (t )]
[ A(t ) K (t ) H (t )]e(t ) G (t ) (t ) K (t ) (t )
~
A(t )e(t ) G (t ) (t ) K (t ) (t ),
~
A(t ) A(t ) K (t ) H (t )
где
Подставляя выражение для e ( t ) в соотношение (2.30) и учитывая, что M [ (t ) T (t )] 0 ,
получим
P ( t ) [ A ( t ) K ( t ) H ( t )] P ( t ) P ( t ) [ A ( t ) K ( t ) H ( t )] T G ( t ) Q ( t ) G T ( t )
(2.31)
K ( t ) R ( t ) K T ( t ).
Теперь коэффициент усиления может быть найден из решения следующей
оптимизационной задачи

6.

S P P(t )
S P [ A(t ) P(t ) K (t ) H (t ) P(t ) P(t ) AT (t ) P(t ) H T (t ) K T (t )
K (t )
K (t )
(2.32)
G (t )Q(t )G T (t ) K (t ) R(t ) K T (t )]
S P [ H (t ) P(t ) P(t ) H T (t ) R(t ) K T (t ) K (t ) R(t )]
S P {K (t ) R(t ) P(t ) H T (t ) [ K (t ) R(t ) P(t ) H T (t )]T } 0.
Уравнение (2.32) превращается в тождество, если
K (t ) R(t ) P(t ) H T (t ) 0
Отсюда оптимальный коэффициент усиления будет иметь вид
K (t ) P(t ) H T (t ) R 1 (t )
Подставляя найденный коэффициент усиления в соотношение (2.31), получим
уравнение
P(t ) A(t ) P(t ) P(t ) AT (t ) G (t )Q(t )GT (t ) K (t ) R(t ) K T (t )
Соотношение (2.33) называется уравнением Риккати.
(2.33)

7. Оптимальный фильтр Калмана (ОФК) в непрерывном времени, оценивающий ошибки стохастической системы

P (t ) A(t ) P(t ) P(t ) AT (t ) G (t )Q(t )G T (t ) K (t ) R(t ) K T (t )
K (t ) P(t ) H T (t ) R 1 (t )
x ˆ (t ) A(t ) xˆ (t ) K (t )[ z (t ) H (t ) xˆ (t )]