Similar presentations:
Модели рационального спектра. Тема 3
1.
Тема 3. Модели рационального спектраМодели рационального спектра – метод параметрического описания данных.
Параметрическая модель ФВР основана на понятии формирующего фильтра.
На входе фильтра – формирующее воздействие
статистиками :
u n , т.е. ВР со стандартными
2
E u n 0 ; E u n u ; u
Формирующее воздействие – белый шум (БШ) :
2
1 , m 0
m
;
0 , m 0
1 , k 0
u m Pu k
0, k 0
На выходе фильтра – уникальный ВР x n с заданными статистиками :
ДПФ
ДПФ
E x n 0 ; E x 2 n 2x ; x m Px k
Фильтр формирует заданные корреляционно-спектральные свойства ВР
x n
Модели формирующего фильтра (ФФ) : 1) уравнение дискретной свертки;
2) линейное разностное уравнение; 3) операторная форма.
2.
Описание ФФ с помощью уравнения дискретной сверткиx n h k u n k ; h n 0 , n 0 - физически реализуемый
БИХ - фильтр
k 0
Описание ФФ с помощью линейного разностного уравнения порядка (p , q)
q
p
x n a k x n k u n b k u n k
k 1
k 1
БИХ часть – АР(p)
КИХ часть – СС(q)
АРСС (p, q) / ARMA (p, q)
Авторегрессия – скользящее среднее порядка (p, q)
Параметры АРСС – модели :
a 1 , a 2 , , a p авторегрессии ;
2) порядок q и коэффициенты b 1 , b 2 , , b q скользящего среднего.
Задача идентификации АРСС модели – по заданным статистикам ВР x n
1) порядок p и коэффициенты
оценить порядок (p, q) модели и ее коэффициенты
3.
Операторная форма описания ФФОператор запаздывания на k шагов времени :
k
k
x n k z
x n ; u n k z u n
Линейное разностное уравнение в терминах оператора запаздывания :
p
1 x n a k z
k 1
k
q
x n 1 u n b k z k u n
Свойство линейности оператора запаздывания :
k 1
q
p
k
k
1 x n a k z x n 1 u n b k z u n
k 1
k 1
Операторная форма АРСС модели :
x n Bq z u n
Ap z
1
1
Полиномы авторегрессии и скользящего среднего степеней p и q :
p
q
Ap z 1 1 a k z k ; Bq z 1 1 b k z k
k 1
k 1
z – комплексная A z 1 ; B z 1 - ДПЛ последовательностей
p
q
переменная
a 1 , , a p и b 1 , , b q
4.
Системная функция ФФ в комплексной областиH z
1
1
L x n Bq z
k - ДПЛ импульсной
h
k
z
1
характеристики ФФ
L u n Ap z
k 0
z m exp j 2 m K - m-е дискретное значение комплексной
переменной на единичной окружности
Передаточная функция ФФ в частотной области – ДПФ ИХ
Bq m
k m
1
H m H z z z m
h k exp j 2
Ap m k 0
K
ДПФ полиномов авторегрессии и скользящего среднего
p
k m
1
Ap m Ap z z z m 1 a k exp j 2
K
k 1
0 m K 1
Bq m Bq z
1
k m
z z m 1 b k exp j 2
K
k 1
q
5.
Px mСПМ временного ряда на выходе ФФ
2
2
u t Pu m Bq m Ap m ; 0 m
K 1
Энергетический спектр ВР на выходе ФФ – дробно – рациональная функция :
2
q
Px m
1 b k exp j 2 k m K
u2 t
k 1
p
1 a k exp j 2 k m K
k 1
Метод формирующего фильтра
Статистическое моделирование ВР
Прогнозирование ВР
Параметрическое спектральное оценивание ВР
6.
Коэффициент корреляции временного ряда на выходе ФФxAR m xMA m , 0 m q
x m
xAR m
,m q
xAR m
p
a k x m k , m 0 - линейная часть
k 1
q m
MA
x
m
b k b k m b m
k 1
q
1 b k
2
,0 m q
- нелинейная часть
k 1
Типы моделей рационального спектра
1. Модели авторегрессии : q = 0 => ARMA(p,0) => AR(p) , p = 1,2 ;
2. Модели скользящего среднего : p = 0 => ARMA(0,q) => MA(q) , q = 1,2 ;
3. Смешанные модели : ARMA(p,q) => p , q = 1,2.
7.
Авторегрессионные модели временного рядаТеорема декомпозиции Уолда – любую АРСС- модель или СС- модель можно
аппроксимировать АР- моделью более высокого порядка.
p
x m
a k x m k , m 1, 2 , , p
k 1
Система линейных нормальных уравнений Юла – Уолкера :
a 1 x 0 a 2 x 1 a p x p 1 x 1
a 1 1 a 2 0 a p p 2 2
x
x
x
x
a 1 x p 1 a 2 x p 2 a p x 0 x p
Матричная форма системы уравнений Юла – Уолкера : R p a p p
T
a p a 1 , a 2 , , a p - вектор-столбец АР- параметров
T
p x 1 , x 2 , , x p - корреляционный вектор-столбец
8.
9.
Теплицева автокорреляционная матрицаx 1
x 0
x 0
x 1
Rp
x p 1 x p 2
x p 1
x p 2
x 0
Алгоритм Левинсона – Дурбина (ЛД)
Шаг 0 : Инициализация. Тестировать АР(1) - модель.
2
2
p 1; a1 1 x 1 ; 1 1 a1 1
Шаг 1 : Тестировать АР – модель текущего порядка. p = p + 1.
p 1
a p p x p a p 1 k x p k 2p 1
k 1
Шаг 2 : Рекурсия Левинсона.
a p k a p 1 k a p p a p 1 p k ; k 1 ; ( p 1)
10.
Шаг 3 : Вычислить дисперсию ошибки линейного прогноза.a p p 1 ; 2p 1 a 2p p 2p 1
Шаг 4 : Критерии продолжения рекурсии. Если
2
2
a p p 1 ; p p 1 2
то идти к Шагу 1. В противном случае закончить вычисления.
Свойства алгоритма Левинсона - Дурбина
3
1. Объем вычислений : алгоритм исключения Гаусса ~ p ; алгоритм ЛД ~
2. Алгоритм рекурсивный по порядку авторегрессии p :
a 1 1 ; 12
a 2 1 ; a 2 2 ; 22
a3 1 ;a3 2 ;a3 3
3. Критерий правильного выбора порядка авторегрессии p :
2
2
p p 1 2
4. Применение смещенной оценки автокорреляционной матрицы R p :
K 1
1
n m v n k v n m k
K k 0
обеспечивает ее положительную полуопределенность.
p
2
; 32
11.
12.
5. Необходимое и достаточное условие положительной полуоопределенностиавтокорреляционной матрицы R p :
a p p 1, p 1, 2 , ; K p a p p - коэффициенты отражения
6. Нули полинома авторегрессии лежат внутри единичной окружности
плоскости комплексной переменной z :
p
Ap z 1
z 1 g k ; g k 1
k 1
В этом случае ФФ 1
Ap m устойчивый, а процесс АР(p) – стационарный.
Основные понятия теории линейного прогноза
Цифровые фильтры линейного прогноза (ЛП) :
p
vˆ pf n p a pf k v n p k - «вперед» (forward) ;
k 1
p
vˆ bp n a bp k v n k - «назад» (backward) ;
k 1
n 1, 2 , , ( N p) - окно обучения фильтров.
13.
Коэффициенты фильтров совпадают для вещественных ВР :a pf k a bp k a p k k 1, 2 , , p
Коэффициенты фильтров оценивают методом наименьших квадратов, т. е.
оптимизируют по критерию минимума дисперсии ошибок ЛП:
N p
2
2
1
2
f
b
p
ep n ep n
2 N p n 1
Ошибки ЛП :
f
f
e p n v n p vˆ p n p
p
v n p a p k v n p k
k 1
- фильтр ошибки ЛП в «прямом» направлении;
p
e bp n v n vˆ bp n v n a p k v n k
k 1
- фильтр ошибки ЛП в «обратном» направлении.
14.
Ap m - передаточная функция ЦФ ошибки ЛП в «прямом» направлении.Фильтр инверсный по отношению к ФФ 1 Ap m
Рекурсия Левинсона для ошибок ЛП в «прямом» и «обратном» направлениях :
e pf n e pf 1 n K p e bp 1 n 1 ; e 0f n v n
b
f
b
b
e p n e p 1 n 1 K p e p 1 n ; e 0 n v n
Решетчатый фильтр (структура)
Свойства решетчатого фильтра :
1. Инверсный по сравнению с ФФ, так называемый обеляющий фильтр.
2. Устойчив к ошибкам вычислений и квантования по сравнению с ФФ.
f
b
3. Ошибки ЛП для текущего порядка ортогональны : E e p n e p n
0
15.
Частный коэффициент корреляции ВР – нормированная корреляция междуv n p и v n за вычетом доли корреляции, вызванной влиянием
промежуточных отсчетов ряда v n p 1 , , v n 1 .
Статистический смысл коэффициента отражения K p a p p - частный
коэффициент корреляции ВР. Альтернативное определение коэффициента
отражения в терминах ошибок ЛП : K p
r pf 1 r pb 1 .
K 1
f
b
e p 1 n k e p 1 n k 1
- частный коэффициент
r pf 1 k 0 K 1
2
корреляции ошибки ЛП
f
e p 1 n k
«вперед».
k 0
K 1
e pf 1 n k e bp 1 n k 1
b
- частный коэффициент
r p 1 k 0 K 1
2
корреляции ошибки ЛП
b
e p 1 n k 1
«назад».
k 0
16.
Геометрический алгоритм БергаШаг 0 : Инициализация. Вычислить начальные значения ошибок ЛП
f
b
2
p 0 ; e0 n e0 n v n ; 0 1
Шаг 1 : Тестировать АР – модель текущего порядка. p = p + 1. Вычислить
выборочные оценки частных коэффициентов корреляции для
b
f
ошибок ЛП «вперед» r p 1 и «назад» r p 1 .
Вычислить выборочную оценку коэффициента отражения
a p p K p r pf 1 r pb 1
Шаг 2 : Рекурсия Левинсона. Вычислить ошибку ЛП для АР- модели
текущего порядка
e pf n e pf 1 n K p e bp 1 n 1
e bp n e bp 1 n 1 K p e pf 1 n
Если p > 1, то вычислить младшие коэффициенты авторегрессии
a p k a p 1 k K p p k ; k 1 ; ( p 1)
17.
Шаг 3 : Вычислить дисперсию ошибки линейного прогноза2p 1 a 2p p 2p 1
Шаг 4 : Критерии продолжения рекурсии. Если
K p 1 ;
2
p
2
p 1
2
то идти к Шагу 1. В противном случае закончить вычисления.
18.
СС(q) - модели временного рядаq
Нерекурсивный ЦФ
v n u n b k u n k ; u n
k 1
Способы оценки СС- параметров :
Bq z
1
v n
1. Решение системы нелинейных уравнений
qk 11 b k b k 1 b 1 D q vMA 1
qk 12 b k b k 2 b 2 D q vMA 2
MA
q 1
b
1
b
q
b
q
1
D
q
v
b q D MA q
q
v
D q 1 b 1 b 2 b q
2
2
2
2
; u
MA
v
0 D q
19.
Шаг 0 : Инициализация. i = 1. Вычислить начальные значения СС- параметров0
b
k 0 ; k 1, 2 , , q
Шаг 1 : Вычислить дисперсию БШ
q
2
i 1
D q 1
b
k ; u2 vMA 0 D q
k 1
Шаг 2 : m = q. Вычислить старший СС- параметр
i
MA
b q D q v
q
Шаг 3 : m = m - 1. Вычислить младший СС- параметр
q m
b i m
b i 1 k b i k m D q vMA m
k 1
Шаг 4 : Цикл по младшим СС- параметрам. Если m > 1, то идти к Шагу 3.
Шаг 5 : Критерии продолжения вычислений. Если m = 1 и хотя бы один
из СС- параметров удовлетворяет неравенству
b
i
k b
i 1
k ; k 1, 2 , , q ,
то i = i +1. Идти к Шагу 1. В противном случае закончить вычисления.
20.
2. Аппроксимация СС- процесса эквивалентной АР- моделью высокого порядкаq
~
1
k
1
Bq z 1 b k z ; A z 1 a~ k z k
k 1
k 1
~
1
1
~
a k a k ; b k b k ; Bq z 1 A z
q
ДПЛ
1 , n 0
~ ~
1
1
~
Bq z A z 1 a n b k a n k
0,n 0
k 1
Фильтр ошибки ЛП «вперед» :
q
~
e qMA n a~K n bq k a~K n k ; q K
k 1
для данных :
a~K 0 1, a~K n , n 1, 2 , , q K
Вектор-столбец СС- параметров :
2
T
~
~
~
MA
n
bq bq 1 , bq 2 , , bq q Arg min
eq
bq n
Система линейных нормальных уравнений : Rq bq q
21.
q v 1, 0 , v 2 , 0 , , v q , 0 T- корреляционный векторRq v m , k
k 1; q - корреляционная матрица
m 1; q
Автокорреляционная оценка СС- параметров (алгоритм Юла - Уолкера) :
q K
v m , k v m k a~K i m a~K i k
i 1
Свойства оценки :
1. Корреляционная матрица теплицева – рационально применять алгоритм ЛД.
2. Смещенная оценка автокорреляции – ФФ устойчивый (минимально-фазовый).
3. Требует достаточно большого порядка (q+K) модели авторегрессии.
Ковариационная оценка СС- параметров :
v m , k
K
a~K i m a~K i k
i q 1
Свойства оценки :
1. Корреляционная матрица является произведением теплицевых матриц.
2. Корреляционная матрица невырожденная если q K 2 .
22.
qДисперсия ошибки ЛП :
~
u2 v 0 , 0 bq k v 0 , k
k 1
3. Оценка СС- параметров методом спектральной факторизации
~
~
b k b k ; b 0 1 ;
2 q ~ ~
u b k b k m , 0 m q
MA
r m k m
0
,m q
2
MA
2
Факторизация в частотной области : Pr
m u t B q m
q
~
B q m b k z k m ; z m e j 2 m K ; 0 m K 1
Факторизация во временной области :
k 0
Факторизация в области комплексной переменной (в терминах ДПЛ) :
MA
Pr
z
1
q
MA
r
m q
m z
m
q
q
m 0
k 0
~
~
m
k
b m z b k z
23.
Основная теорема алгебры : Если конечный степенной рядимеет симметричные коэффициенты
нули
MA
r
MA
Pr
MA
m r
z
1
m , то его
c k образуют взаимно обратные пары, т. е. ряд можно представить в виде
q
~
Pr MA z 1 b 2 q z 1 c k1 z c k1
k 1
q
~
~
B q z 1 b k z k b q z 1 c k1
k 0
k 1
1
~
Взаимосвязь между коэффициентами b k и корнями c k полинома СС
q
устанавливают симметрические функции :
q k 1 q k 2
Vk
~
b q
q
c m 11 c m 21 c m k1
m 1 1 m 2 m 1 1
m k m k 1 1
q
~
k~
q
( 1)
c k ; b q k 1 b
k 1
q V k ; k 1 ; q 1
24.
4. Оценка СС- параметров методом гомоморфного преобразованияШаг 1 : Вычислить энергетический спектр СС- процесса
K 1
mk
MA
MA
Pr
k 2 t r m cos 2
;0 k
K
m 0
Шаг 2 : Вычислить кепстры СС- процесса и его коэффициентов
K 1
K 1
2
mk
MA
MA
ˆ r m ln Pr k cos 2
;
K k 0
K
MA
ˆ
b m ˆ r m 2 ; 0 m K 1
Шаг 3 : Вычислить передаточную функция ФФ для СС- процесса
K 1
mk
Bˆ k 2 t
ˆ
b m cos 2 ; B q k exp Bˆ k
K
m 0
Шаг 4 : Вычислить коэффициенты СС- процесса
2 K 1
mk
~
b m B q k cos 2
;0 m q
K k 0
K
25.
АРСС(p, q) - модели временного рядаСубоптимальные оценки АРСС- параметров
Раздельное оценивание
АР- и СС- параметров
Одновременное оценивание
АР- и СС- параметров
Раздельное оценивание АР- и СС- параметров :
1. оценивание АР- параметров модифицированным МНК Юла – Уолкера ;
2. формирование остаточного ВР с помощью нерекурсивного фильтра ;
3. оценивание СС- параметров по остаточному ВР.
Модифицированный МНК Юла – Уолкера
Ошибка оценивания АР- параметров :
p
p m ˆ r m a k ˆ r m k , q 1 m M
̂r m
k 1
- несмещенная оценка АКФ ;
p << M – переопределенная СЛНУ
M
T
2
a p a 1 , a 2 , , a p Arg min
p m
a p m q 1
26.
Остаточный ВР – модель СС(q)Нерекурсивный ЦФ :
r n
Ap z
1
s n
p
q
k 1
k 1
s n r n a k r n k u n b k u n k
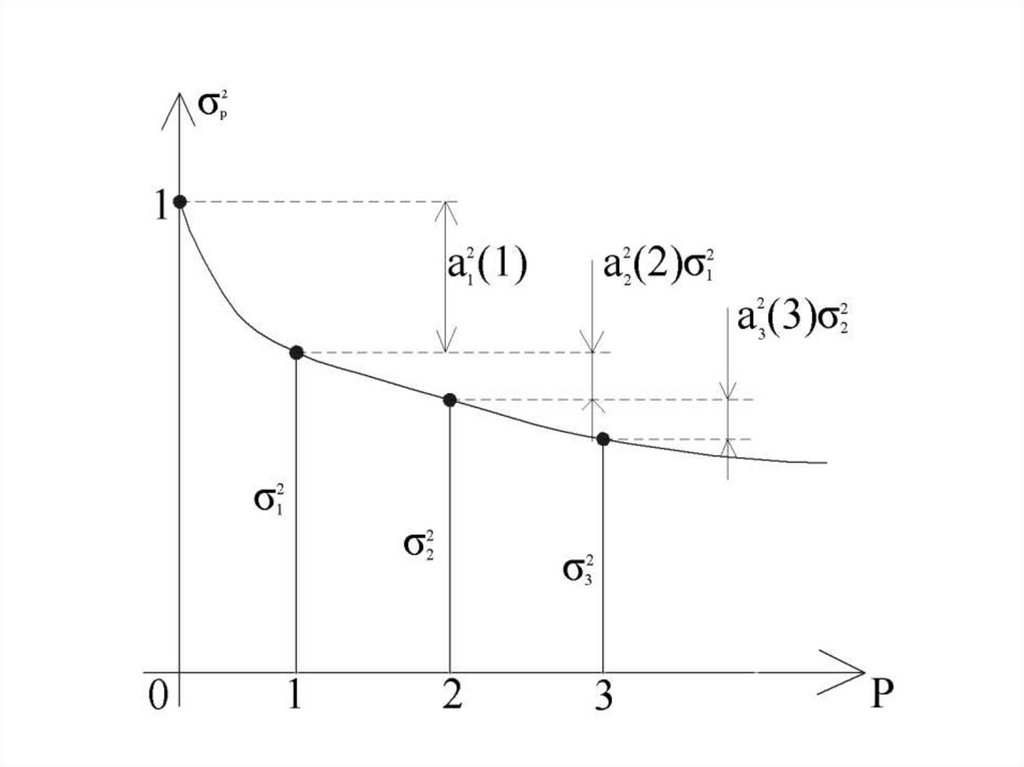
АКФ остаточного ВР :
p p
a k a i ˆ r m i k , m q
s m k 0 i 0
0
, m q

























 mathematics
mathematics








