Similar presentations:
Общая постановка задачи. Разработка адаптивных систем управления объектами реального мира
1.
Общая постановка задачиОбщая цель: разработка адаптивных систем управления объектами реального мира (в том числе
технологическими агрегатами), имеющими параметрическую неопределенность.
Задача состоит в поддержании требуемого качества управления при следующих условиях:
1) значения параметров объекта неизвестны;
2) имеются возмущения различной природы и шумы измерений.
Адаптивные системы управления с эталонной моделью - Model reference adaptive control
(MRAC) - это основа для разработки систем параметрической адаптации.
Общее описание объекта:
x t f x Bu
x(t) ∈ Rn – вектор состояний,
u(t) ∈ Rm – вектор сигналов управления,
B ∈ Rn x m – матрица управления
Nhan T. Nguyen Model-Reference Adaptive Control. A Primer. Springer, 2018.
1
2.
Общая постановка задачиВиды неопределенности:
1) параметрическая неопределенность – параметры неизвестны, но известна структура
объекта;
2) структурная неопределенность – ни параметры, ни структура неизвестны;
3) согласованная неопределенность – может быть скомпенсирована выбором управления:
x t f x B u * T x
(1)
где x(t) ∈ Rn – вектор состояния, u(t) ∈ Rm – вектор управления, B ∈ Rn x m – матрица
управления, θ∗ ∈ Rp x m – матрица неизвестных параметров, и ω(x) ∈ Rp – известный
измеримый ограниченный регрессор;
4) несогласованная неопределенность – не может быть полностью скомпенсирована
управлением:
x t f x Bu * T x
(2)
матрица управления B ∈ Rn x m неквадратная, n > m, или B ∈ Rn x n – квадратная матрица
неполного ранга (обратной матрицы не существует).
2
3.
Общая постановка задачиСистемы прямого и непрямого адаптивного управления с эталонной моделью:
1) Непрямые предполагают определение параметров объекта, модель которого
записывается в виде линейной регрессии, а затем вычисление параметров регулятора:
y t T t
(3)
2) Прямые подразумевают "идентификацию" параметров регулятора в режиме реального
времени, что также записывается как регрессия (3).
Пример 1.
y t a1 y t a0 y t ku t
y t a0 y t a1 y t ku t a0
a1
T
y t
k y t T t
u t
(4)
t
Компоненты регрессора – это любые линейные или нелинейные функции. Поэтому
нелинейные объекты также могут быть параметризованы в таком виде.
3
4.
Общая постановка задачиПример 2.
x t
T
k r
t
r t
e t
t
t
u t K p e t Ki e d K d e t K p K i K d e d T t
0
0
e t
u t k x x t k r r t k x
(5)
Если вектор состояния недоступен, а измеряется лишь выход объекта, то все равно
существуют подходы для получения примененной выше параметризации.
4
5.
Когда имеет смысл применять нейронные сети для решения задач управления?Простейший случай адаптивного управления с эталонной моделью
Рассмотрим проблему управления
параметрами по координатам состояния:
линейным
объектом
с
x Ax Bu,
постоянными
(9)
x ∈ Rn – вектор координат состояния
u ∈ R – сигнал управления,
A ∈ Rn×n – неизвестная матрица состояний,
B ∈ Rn×1 – неизвестный вектор управления
Допущение 1:
– значения A и B неизвестны и постоянны, (A, B) – управляемая пара.
– вектор координат состояния x измерим.
Эталонную модель зададим в следующем виде:
xref Aref xref Bref r,
(10)
xref ∈ Rn – вектор координат состояния эталонной модели,
r ∈ R – сигнал задания на контур управления,
Bref ∈ Rn×1 – матрица управления эталонной модели полного
столбцового ранга.
Aref ∈ Rn×n – Гурвицева матрица состояний эталонной модели.
Уравнение в отклонениях:
eref x xref Ax Bu Aref xref Bref r Ax Bu Aref xref Bref r Aref x Aref x Aref eref B u B† A Aref x B† Bref r ,
u B† A Aref x B† Bref r k x x k r r T eref Aref eref
5
(11)
6.
Когда имеет смысл применять нейронные сети для решения задач управления?Базовые законы настройки
Условия Эрцбергера:
A Bk x Aref ; Bkr Bref .
(12)
Закон управления (9) определим как:
u kˆ x x kˆ r r ˆ T
(13)
k̂ x∈ Rm×n, k̂r ∈ Rm×1 – настраиваемые параметры.
Параметризованное уравнение в отклонениях:
eref Aref eref B T , T ˆ T T
(14)
Кандидат в функции Ляпунова:
T
V eref
Peref B T 1
(15)
T
Aref
P PAref Q
Производная функции Ляпунова:
T
T
T
V eref
Peref eref
Peref 2 B T 1 eref
ArefT P PAref eref 2erefT P sgn B B T 2 B T 1 (16)
B
Базовый закон настройки:
ˆ eT Psgn B
ref
T
V eref
Qeref 0, V ограничена
6
(17)
7.
Когда имеет смысл применять нейронные сети для решения задач управления?Базовые законы настройки
- компенсируется неопределенность параметров объекта, обеспечивается
асимптотическая сходимость ошибки слежения к нулю;
- в случае возмущений и шумов измерений необходимо использовать робастные
модификации (σ-, e-, оптимальные и т.д.), чтобы избежать дрейфа настраиваемых
параметров регулятора. В этом случае ошибка слежения сходится к ограниченному
множеству.
- нет необходимости применять какие-либо другие регуляторы (например, на
основе нейронных сетей).
7
8.
Когда имеет смысл применять нейронные сети для решения задач управления?Адаптивное управление с эталонной моделью нелинейными объектами
Рассмотрим задачу управления по вектору координат состояния нелинейным
объектом с неизвестными постоянными параметрами:
x Ax B u f x ,
(18)
f(x) ∈ R - неопределенность с известной структурой и
неизвестными параметрами
f (x) может быть линейно параметризована (регрессия линейна, но регрессор нелинеен):
p
f x i i * T x
(19)
i 1
где Θ* = [ θ1 , θ2, . . ., θp]T ∈ Rp – вектор неизвестных параметров
Φ (x) = [φ1(x), φ2(x), . . ., φp(x)]T ∈ Rp - вектор известных ограниченных базисных функций.
Эталонная модель определена следующим образом:
xref Aref xref Bref r,
Уравнение в отклонениях:
eref x xref Aref eref B u * T x B† A Aref x B† Bref r ,
u B† A Aref x B† Bref r * T x k x x k r r * T x
T * T x ubaseline uadaptive
eref Aref eref
8
(20)
9.
Когда имеет смысл применять нейронные сети для решения задач управления?Адаптивное управление с эталонной моделью нелинейными объектами
Закон управления для (18) определен как:
ˆ T
ˆ T x
ˆ T x
u kˆ x x kˆ r r
(21)
k̂ x∈ Rm×n, k̂r ∈ Rm×1, ̂ ∈ Rp×1 – настраиваемые параметры.
Параметризованное уравнение в отклонениях:
ˆ T * T
eref Aref eref B T B T x , T ˆ T T , T
(22)
Кандидат в функции Ляпунова:
T
V eref
Peref B T 1 B T 1
A P PAref Q
T
ref
(23)
Производная функции Ляпунова:
T
T
V eref
Peref eref
Peref 2 B T 1 2 B T 1
T
eref
ArefT P PAref eref 2erefT P sgn B B T 2 B T 1 2erefT P sgn B B T x 2 B T 1 (24)
B
B
T
T
T
eref
Qeref 2eref
Psgn B B T 2 B T 1 2eref
Psgn B B T x 2 B T 1
Базовые законы настройки:
ˆ eT Psgn B ,
ˆ x eT Psgn B
ref
ref
V e Qeref 0, V ограничена
T
ref
9
(25)
10.
Когда имеет смысл применять нейронные сети для решения задач управления?Свойства полученной системы управления
- компенсируется нелинейность и неопределенность параметров объекта, обеспечивается
асимптотическая сходимость ошибки слежения к нулю;
- в случае возмущений и шумов измерений необходимо использовать робастные модификации (σ-,
e-, оптимальные и т.д.), чтобы избежать дрейфа настраиваемых параметров регулятора. Ошибка
слежения сходится к ограниченному множеству.
Но что мы действительно знаем о регрессоре неопределенности Φ(x)?
1) Если мы знаем структуру нелинейности, то мы можем использовать
вышеупомянутые линейные регрессии и адаптивные законы для компенсации как
неопределенности, так и нелинейности.
Пример 3. Проблема Wing Rock.
Явление сваливания по крену крыла дельта-видной формы:
x1 0
x 0
2
1 x1 0
u T x ,
0 x2 1
(26)
где x1 – крен, x2 – динамика крена, u – управление, Ф(x) = [x1, x2, | x 1| x2, | x2 | x2, x13]T.
2) Если мы не знаем структуру нелинейности, то мы не можем сформировать
правильный регрессор Φ(x). Но мы знаем x. Поэтому нам необходимо использовать
некоторые другие структуры вместо f(x)=ΘTΦ (x), которые обеспечивают универсальные
аппроксимационные свойства. Например, нейронные сети.
10
11. Нейронные сети. Модель нейрона МакКаллока-Питтса
Почему нейронные сети применяют для задач управления?Нейронные сети. Модель нейрона МакКаллока-Питтса
m
s i x i b,
i 1
y f ( s ).
xi – i-й входной сигнал
wi - i-й весовой коэффициент
b - смещение
s – взвешенная сумма
f - функция активацииn
y - выходной сигнал нейрона
сигмоидальная
гиперболический тангенс
разновидности линейной функции
McCULLOCH W., PITTS W. A Logical Calculus of the Ideas Immanent in Nervous Activity // Bull. Math. Biophys. – 1943. – Vol. 5. – P. 115–133.
11
12.
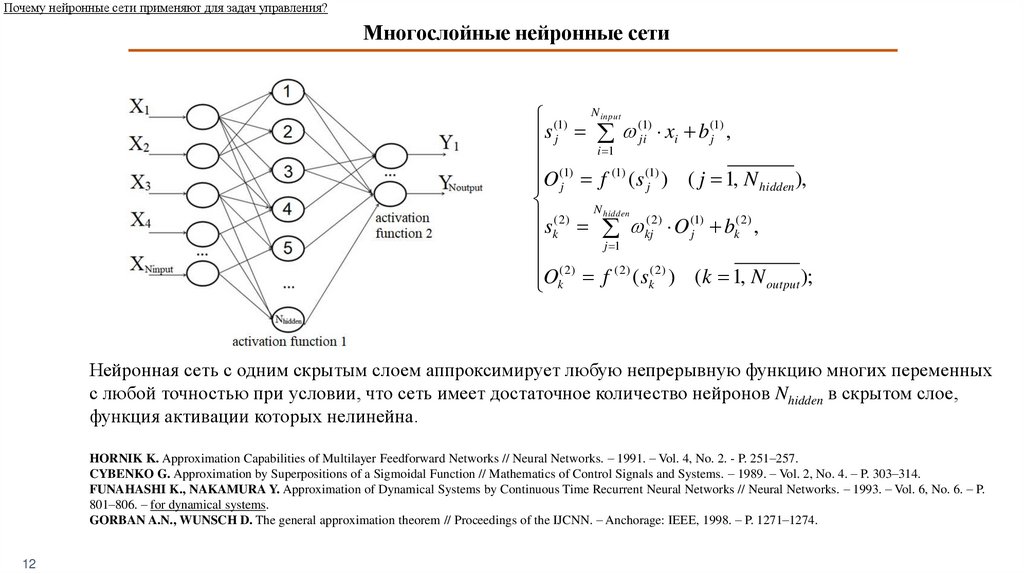
Почему нейронные сети применяют для задач управления?Многослойные нейронные сети
(1) N input (1)
(1)
s
x
b
j
ji
i
j ,
i 1
O (j1) f (1) ( s (j1) ) ( j 1, N hidden ),
N hidden
sk( 2) kj( 2 ) O (j1) bk( 2 ) ,
j 1
( 2)
( 2)
( 2)
Ok f ( sk ) (k 1, N output );
Нейронная сеть с одним скрытым слоем аппроксимирует любую непрерывную функцию многих переменных
с любой точностью при условии, что сеть имеет достаточное количество нейронов Nhidden в скрытом слое,
функция активации которых нелинейна.
HORNIK K. Approximation Capabilities of Multilayer Feedforward Networks // Neural Networks. – 1991. – Vol. 4, No. 2. - P. 251–257.
CYBENKO G. Approximation by Superpositions of a Sigmoidal Function // Mathematics of Control Signals and Systems. – 1989. – Vol. 2, No. 4. – P. 303–314.
FUNAHASHI K., NAKAMURA Y. Approximation of Dynamical Systems by Continuous Time Recurrent Neural Networks // Neural Networks. – 1993. – Vol. 6, No. 6. – P.
801–806. – for dynamical systems.
GORBAN A.N., WUNSCH D. The general approximation theorem // Proceedings of the IJCNN. – Anchorage: IEEE, 1998. – P. 1271–1274.
12
13.
Почему нейронные сети применяют для задач управления?Многослойные нейронные сети – математически обоснованные универсальные аппроксиматоры
1) Такая нейронная сеть представляет собой набор
логистических регрессий, выходы которых затем
взвешиваются для формирования выходного
сигнала.
2) Скрытый слой предназначен для преобразования
входных признаков в представление более высокой
размерности, чтобы сделать первоначально
неразделимые данные линейно-разделимыми.
COVER T. Geometrical and Statistical Properties of Systems of Linear Inequalities with Applications in Pattern Recognition // IEEE Transactions on Electronic Computers. –
1965. – EC-14. – P. 326–334.
13
14. «Зоопарк» нейросетевых архитектур
Какую структуру сети выбрать?«Зоопарк» нейросетевых архитектур
Van Veen, F. & Leijnen, S. (2019). The Neural Network Zoo. Retrieved from https://www.asimovinstitute.org/neural-network-zoo
14
15. Нейронные сети. Области применения
Какую структуру сети выбрать?Нейронные сети. Области применения
1) Классификация - распознавание образов (изображения, аудио), сегментация
изображений, удаление шума, анализ тональности текста, обработка
естественного языка. Сверточные сети и автоэнкодеры. Извлечение признаков
из исходных данных с использованием минимально возможного числа
настраиваемых параметров.
2) Кластеризация - состязательные сети и сети Кохонена. Цель - поиск похожих
примеров и объединение их в кластеры.
3) Аппроксимация регрессионных зависимостей - предсказание и
идентификация объектов реального мира, обработка естественного языка.
Рекуррентные сети (gru, lstm, simpleRNN). Цель - запомнить необходимую
информацию на как можно более долгий срок.
4) Генерация "новых" данных - создание картин, музыки и т.д. Генеративносостязательные сети (GAN), вариативные автоэнкодеры.
5) Решение задач управления. Неглубокие многослойные сети. Проблема
заключается в том, где взять ground-truth (правильные ответы) для обучения
сети.
15
16. Нейронные сети для решения задач управления
Как обучать нейронную сеть?Нейронные сети для решения задач управления
1) Учитывая (18)-(25), нейронные сети (которые должны заменить собой
f (x) = ΘTФ(x)) не могут быть обучены заранее (автономно), поскольку
получение адекватной обучающей выборки – это весьма нетривиальная
задача. «Правильные ответы» - значения f (x) - недоступны.
2) Второй метод Ляпунова будет использоваться как для (а) получения новых
законов (вместо обычного «обратного распространения») для настройки
параметров нейронной сети (как известно, такой метод позволяет избавиться
от необходимости знать идеальные значения параметров регулятора), так и
для (б) обеспечения устойчивости замкнутой системы. Таким образом,
нейронная сеть будет обучаться в режиме онлайн (оперативно).
3) В случае онлайн-обучения нейронная сеть является лишь мгновенным
аппроксиматором текущей нелинейности и неопределенности объекта. Она
не аппроксимирует всю "кривую". Поэтому глубокие сети с
«долговременной» памятью не требуются.
16
4) Скрытый слой нейронной сети содержит нелинейную функцию активации
для аппроксимации нелинейностей.
17. Нейронные сети для решения задач управления
Как обучать нейронную сеть?Нейронные сети для решения задач управления
1) Lewis F. W., Jagannathan S., Yesildirak A. Neural network control of robot manipulators
and non-linear systems. – CRC press, 1999.
2) Ge, S. S., Hang, C. C., Lee, T. H., Zhang, T. Stable adaptive neural network control.
Vol. 13. Springer Science & Business Media 2013.
3) Nhan T. Nguyen Model-Reference Adaptive Control. A Primer. Springer, 2018.
4) Hovakimyan N., Calise A. J. Adaptive output feedback control of uncertain multi-input
multi-output systems using single hidden layer neural networks // Proceedings of 2002
American Control Conference (IEEE Cat. No. CH37301). – IEEE, 2002. – Vol. 2. –
P. 1555-1560.
5) Eugene Lavretsky, Kevin A. Wise Robust and Adaptive Control with Aerospace
Applications. Springer, 2013.
6) Gezer B. R., Kutay A. T. Single hidden layer neural network based model reference
adaptive controller for estimation of periodic disturbances // AIAA Scitech 2019 Forum. –
2019. – P. 1-13.
17
18.
Как обучать нейронную сеть?Адаптивное управление с эталонной моделью нелинейными
объектами на базе нейросетевого компенсатора
Рассмотрим задачу управления по координатам состояния нелинейным объектом
с постоянными неизвестными параметрами:
x Ax B u f x ,
f(x) ∈ R – неопределенность с неизвестными параметрами и структурой
f (x) может быть аппроксимирована нейронной сетью:
f x W T V T x ,
(27)
N
ε – ошибка аппроксимации, εN – верхняя граница, W и V – неизвестные идеальные значения параметров.
x b1
-ε
sigmoid
18
x1
x2
T
xN 1 ; V T x b 2 1 2
1v
v
V 1,1
v
N 1,1
Nv 2
1w
v1, N 2
w1
;
W
.
w
vN 1, N 2
N2
N 2
T
19.
Как обучать нейронную сеть?Адаптивное управление с эталонной моделью нелинейными
объектами на базе нейросетевого компенсатора
Определим нейросетевую оценку f (x) как:
ˆf x Wˆ T Vˆ T x
(28)
где V̂ , Ŵ - фактические значения параметров сети, полученные с помощью алгоритма обучения.
Учтем, что V̂ , Ŵ - это оценки идеальных значений параметров, и определим ошибки оценивания выхода и
параметров как
ˆ T Vˆ T x W T V T x , V Vˆ V , W Wˆ W
e W
(29)
Необходима линейная зависимость ошибки от настраиваемых параметров для вывода алгоритма обучения
сети. Но V входит в уравнение ошибки через сигмоидальную функцию.
Определим ошибку скрытого слоя для текущего x как:
ˆ V T x Vˆ T x
Применим разложение σ(x) в ряд Тейлора для текущего x:
(30)
2
d z
V T x Vˆ T x ' Vˆ T x V T x O V T x , ' ˆz
dz z ˆz
Получим:
19
2
2
' Vˆ T x V T x O V T x ' V T x O V T x
(31)
(32)
20.
Как обучать нейронную сеть?Адаптивное управление с эталонной моделью нелинейными
объектами на базе нейросетевого компенсатора
Определим эталонную модель как:
xref Aref xref Bref r,
Уравнение в отклонениях:
eref x xref Aref eref B u W T V T x B† A Aref x B† Bref r ,
u B† A Aref x B† Bref r W T V T x k x x k r r W T V T x
W V x ubaseline uadaptive
T
T
T
Запишем закон управления как:
ˆ T W
ˆ T Vˆ T x
u kˆ x x kˆ r r Wˆ T Vˆ T x
(33)
(34)
k̂ x∈ Rm×n, k̂r ∈ Rm×1, ̂ ∈ Rp×1 , V̂ ∈ R(N1+1)×(N2+1), Ŵ ∈ R(N2+1)×1 - настраиваемые параметры.
Параметризованное уравнение в отклонениях:
eref Aref eref B T BWˆ T Vˆ T x BW T V T x B
Vˆ x BW Vˆ x ' Vˆ x V x B
A e B BW Vˆ x ' Vˆ x Vˆ x BWˆ ' Vˆ x V x B
Aref eref B T B W W
T
T
T
ref
20
ref
T
T
T
T
T
T
T
T
T
T
T
(35)
21.
Как обучать нейронную сеть?Адаптивное управление с эталонной моделью нелинейными
объектами на базе нейросетевого компенсатора
Выберем кандидата в функции Ляпунова:
V eref , ,V ,W eTref Peref B T 1 B trace V T v 1V B trace W T w1W
T
Aref
P PAref Q
Ее производная:
(36)
V eref , ,V ,W eTref Qeref 2erefT P B T BW T Vˆ T x ' Vˆ T x Vˆ T x BWˆ T ' Vˆ T x V T x B
2 B T 1 2 B trace V T v 1V 2 B trace W T w1W
(37)
T
eTref Qeref 2 B T eref
Psgn B 1 2trace B W T Vˆ T x ' Vˆ T x Vˆ T x eTref Psgn B w1W
2trace B V T xeTref Psgn B Wˆ T ' Vˆ T x v 1V 2eTref PB
Законы настройки имеют вид:
ˆ eT Psgn B ,
ref
T
Vˆ v xeref
Psgn B Wˆ T ' Vˆ T x ,
T
Wˆ w Vˆ T x ' Vˆ T x Vˆ T x eref
Psgn B .
21
(38)
22.
Как обучать нейронную сеть?Адаптивное управление с эталонной моделью нелинейными
объектами на базе нейросетевого компенсатора
Тогда:
V eref , ,V ,W eTref Qeref 2 B erefT P min Q eref
2
2 PB eref 0
(39)
Таким образом:
V eref , ,V ,W 0 if
eref
2 PB 0
min Q
(40)
Даже если исключить из рассмотрения возмущения и шумы измерений, ошибка
слежения может быть сведена только к множеству (не к нулю). Возможен дрейф
настраиваемых параметров. И полученные адаптивные законы должны быть защищены от
него с помощью робастных модификаций.
Когда мы знаем правильный регрессор для нелинейного оператора, мы не
сталкиваемся с такой проблемой. Ошибка слежения сходится к нулю без каких-либо
модификаций.
Устойчивость систем управления на основе нейронных сетей должна быть
аналитически доказана. Адаптивные законы должны быть выведены для каждой задачи (для
учета начальных условий, шума измерений, возмущений и т.д.).
Подобные рассуждения для RBF сетей, для MIMO объектов, для случая
возмущений можно найти в вышеупомянутых книгах и статьях.
22
23.
Применение глубоких нейронных сетей?1) Joshi G., Virdi J., Chowdhary G. Design and flight evaluation of deep model reference
adaptive controller //AIAA Scitech 2020 Forum. – 2020.
2) Joshi G., Chowdhary G. Deep model reference adaptive control //2019 IEEE 58th
Conference on Decision and Control (CDC). – IEEE, 2019. – P. 4601-4608.
3) Joshi G., Chowdhary G. Stochastic Deep Model Reference Adaptive Control //arXiv
preprint arXiv:2108.03120. – 2021.
Глубокие нейронные сети различных структур и типов (сверточные, рекуррентные
и т.д.) могут быть применены для решения задач управления.
Главный вопрос все тот же: как получить "правильные" ответы?
Авторы используют аппроксимацию нелинейности на основе линейной регрессии
для генерации таких "ответов" для глубоких нейронных сетей. Скрытый слой обучается.
Направления дальнейших исследований?
1) Gaudio J. E. et al. Connections between adaptive control and optimization in machine
learning //2019 IEEE 58th Conference on Decision and Control (CDC). – IEEE, 2019. – С. 45634568.
2) Annaswamy A. M., Fradkov A. L. A Historical Perspective of Adaptive Control and
Learning //arXiv preprint arXiv:2108.11336. – 2021.
23
24.
Численные экспериментыПусть объект управления и эталонная модель определены следующим образом:
x1 0 1 x1 0 x1ref 0 1 x1ref 0
x 2 1 x 2 u, x 8 4 x 8 r,
2 2 ref
2 ref
2
Численные эксперименты были проведены для следующих систем управления: 1) линейный регулятор с
настраиваемыми параметрами, 2) регулятор – нейронная сеть, 3) идеальный линейный регулятор:
ulinear kˆ x x kˆ r r ˆ T ,
ˆ eT Psgn B , ˆ 0 0
ref
T
Vˆ v xeref
Psgn B Wˆ T ' Vˆ T vVˆ ,
T
Wˆ w Vˆ T ' Vˆ T Vˆ T eref
Psgn B wVˆ
Полученные результаты приведены ниже:
24
u NN Wˆ T Vˆ T ,
3
uideal k x x kr r T , 1,5
4
25.
Численные экспериментыПусть объект управления и эталонная модель определены следующим образом:
x1 0 1 x1 0 x1ref 0 1 x1ref 0
x 2 1 x 2 u, x 8 4 x 8 r,
2 2 ref
2 ref
2
Численные эксперименты были проведены для следующих систем управления: 1) линейный регулятор с
настраиваемыми параметрами, 2) регулятор – нейронная сеть, 3) идеальный линейный регулятор:
ulinear kˆ x x kˆ r r ˆ T ,
ˆ eT Psgn B
ˆ , ˆ 0 0
ref
T
Vˆ v xeref
Psgn B Wˆ T ' Vˆ T vVˆ ,
T
Wˆ w Vˆ T ' Vˆ T Vˆ T eref
Psgn B wVˆ
Полученные результаты приведены ниже:
25
u NN Wˆ T Vˆ T ,
3
uideal k x x kr r T , 1,5
4
26.
Численные экспериментыОпределим объект и эталонную модель следующим образом (wing rock):
x1ref 0
1 x1ref 0
x1 0 1 x1 0
T
u
x
,
r,
x 0 0 x 1
2
2
x2 ref 5,3 3,25 x2 ref 5,3
T 3,63 8,58 20,2 21,9 51,9 ; x x1
x2
x1 x2
x2 x2
x13 .
Численные эксперименты были проведены для следующих систем управления 1) линейный аппроксиматор с
настраиваемыми параметрами (структура регрессора Φ(x) нелинейности известна), 2) нейросетевой компенсатор
нелинейности (структура регрессора Φ(x) неизвестна), 3) идеальный компенсатор нелинейности и неопределенности:
ulinear k x x kr r x ,
ˆT
ˆ x eT Psgn B ,
ˆ 0 0
ref
Vˆ xe Psgn B Wˆ ' Vˆ x Vˆ ,
Wˆ Vˆ x ' Vˆ x Vˆ x e Psgn B Wˆ
u NN k x x kr r Wˆ T Vˆ T ,
v
T
w
Полученные результаты:
26
T
ref
T
T
v
T
T
T
ref
w
5,3
uideal k x x kr r x , k x 3,25 ,
kr 5,3
T
27.
Численные экспериментыОпределим объект и эталонную модель следующим образом (wing rock):
x1ref 0
1 x1ref 0
x1 0 1 x1 0
T
u
x
,
r,
x 0 0 x 1
2
2
x2 ref 5,3 3,25 x2 ref 5,3
T 3,63 8,58 20,2 21,9 51,9 ; x x1
x2
x1 x2
x2 x2
x13 .
Численные эксперименты были проведены для следующих систем управления 1) линейный аппроксиматор с
настраиваемыми параметрами (структура регрессора Φ(x) нелинейности известна), 2) нейросетевой компенсатор
нелинейности (структура регрессора Φ(x) неизвестна), 3) идеальный компенсатор нелинейности и неопределенности:
ˆ T x ,
ulinear k x x kr r
ˆ x eT Psgn B
ˆ ,
ˆ
ref
0 0
Vˆ xe Psgn B Wˆ ' Vˆ x Vˆ ,
Wˆ Vˆ x ' Vˆ x Vˆ x e Psgn B Wˆ
u NN k x x kr r Wˆ T Vˆ T ,
v
T
w
Полученные результаты:
27
T
ref
T
T
v
T
T
T
ref
w
5,3
uideal k x x kr r x , k x 3,25 ,
kr 5,3
T
28.
Выводы1) нет необходимости применять нейронные сети для управления: (а) линейными
объектами с постоянными неизвестными параметрами и (б) нелинейными объектами с
постоянными неизвестными параметрами, когда регрессор нелинейности полностью
известен.
2) нейронные сети являются универсальными аппроксиматорами, поэтому, когда
регрессор нелинейности неизвестен, нелинейность с неизвестными параметрами может
быть аппроксимирована с их помощью. Во избежание дрейфа параметров в законах
адаптации должны использоваться робастные модификации.
3) нейронные сети не могут быть обучены заранее (offline), поскольку
"правильные ответы" (ground-truth) недоступны.
4) сеть обучается онлайн, и второй метод Ляпунова используется как для (а)
получения новых законов настройки параметров нейронной сети (такой метод позволяет
избавиться от необходимости знать идеальные значения параметров регулятора), так и для
(б) гарантирования устойчивости замкнутой системы.
5) нейронная сеть является лишь мгновенным аппроксиматором текущей
нелинейности и неопределенности объекта. Поэтому глубокие сети с долговременной
памятью не требуются.
28



























 mathematics
mathematics








