Similar presentations:
Динамические нейронные сети и их аттракторы
1. Динамические нейронные сети и их аттракторы
Резник Александр МихайловичИнститут проблем математических
машин и систем НАН Украины
отдел Нейротехнологий
neuro@immsp.kiev.ua
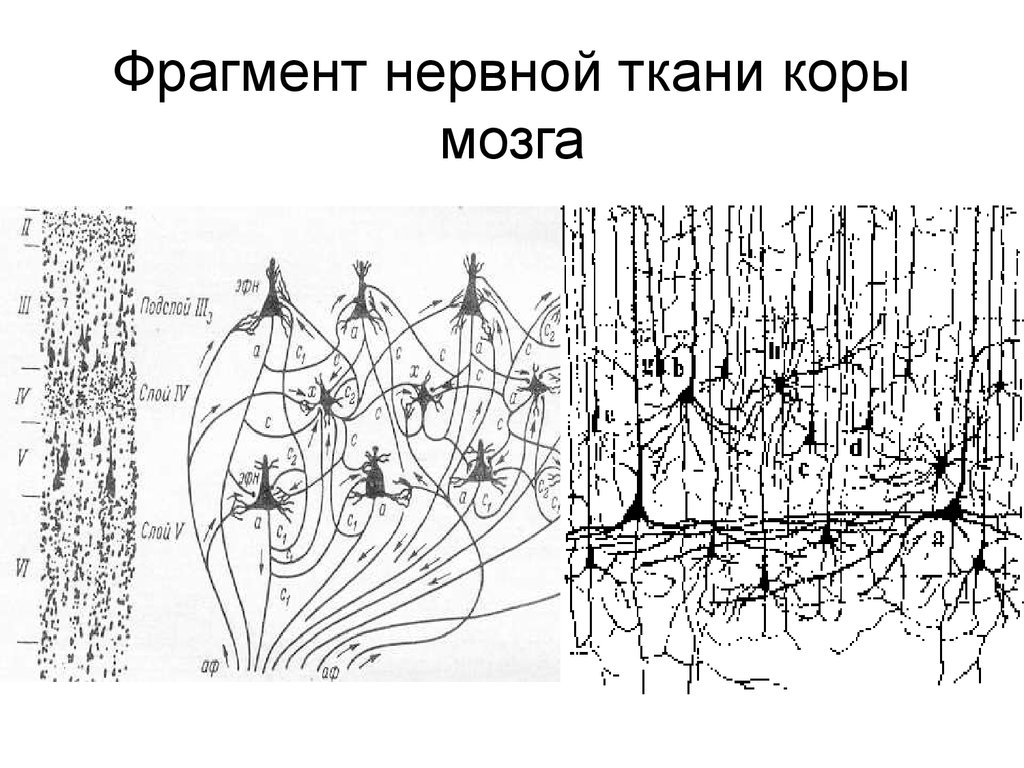
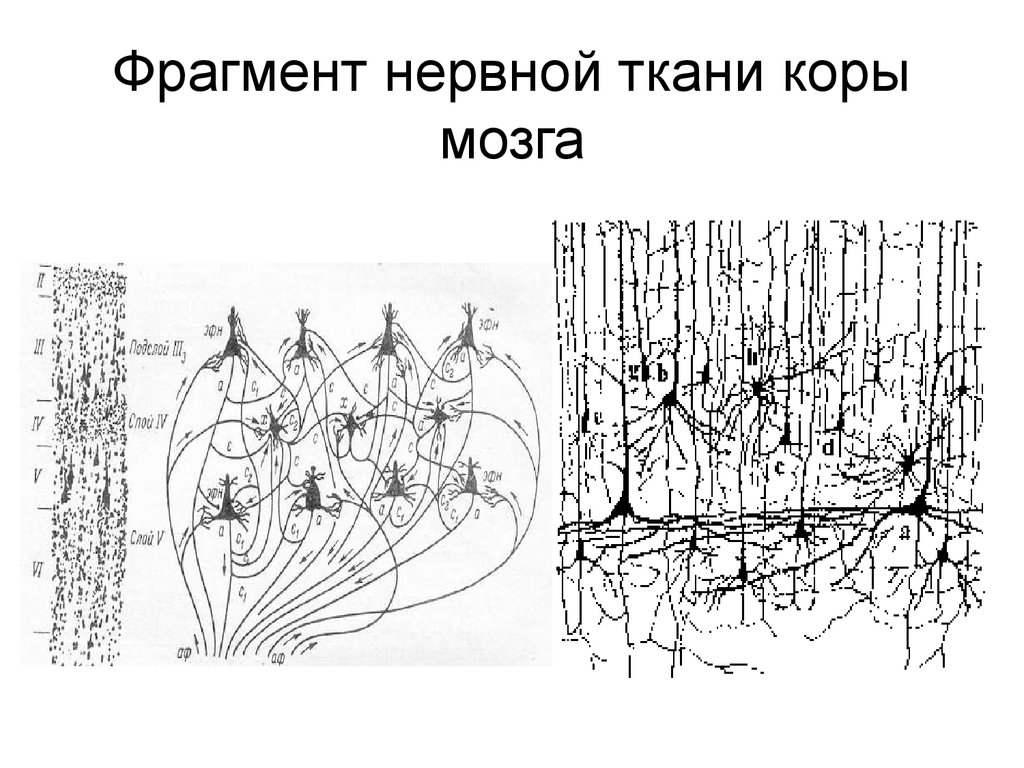
2. Фрагмент нервной ткани коры мозга
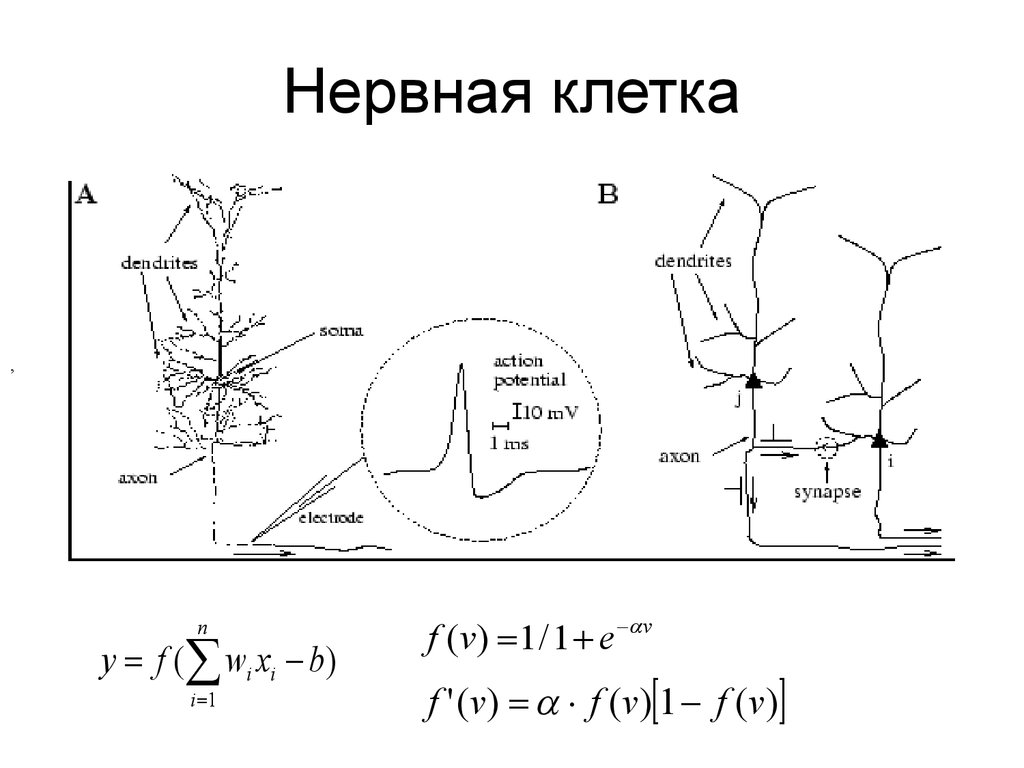
3. Нервная клетка
,n
y f ( wi xi b)
i 1
f ( v ) 1 / 1 e v
f ' (v) f (v) 1 f (v)
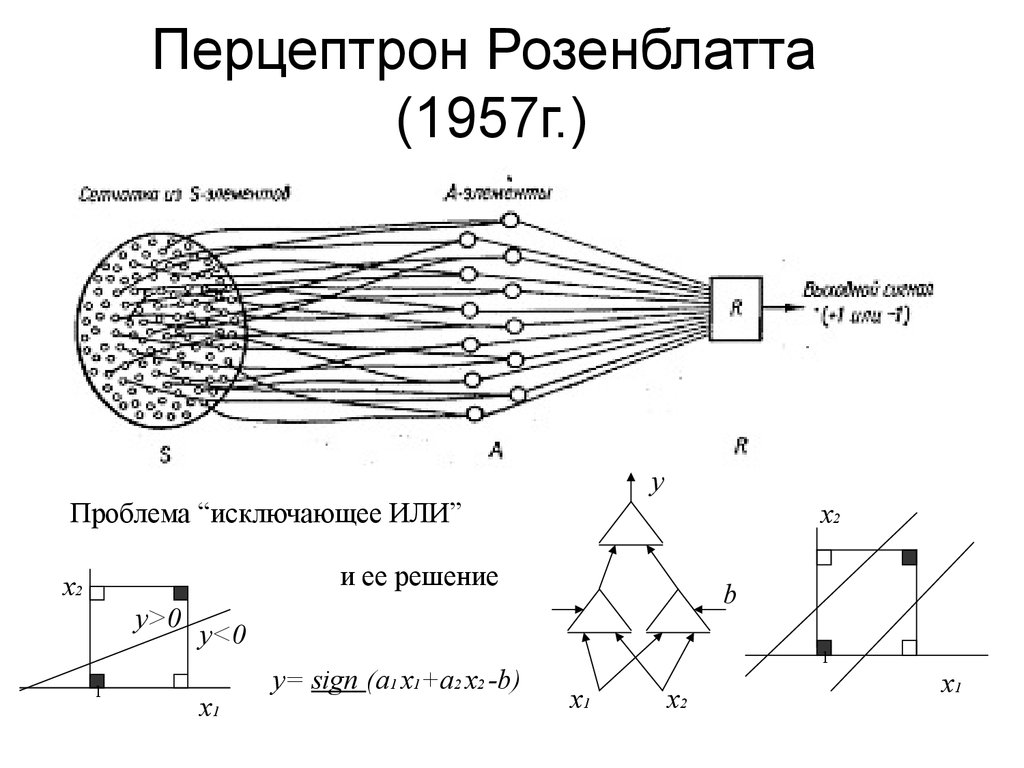
4. Перцептрон Розенблатта (1957г.)
yПроблема “исключающее ИЛИ”
x2
и ее решение
x2
y>0
1
b
y<0
x1
y= sign (a1 x1+a2 x2 -b)
1
x1
x2
x1
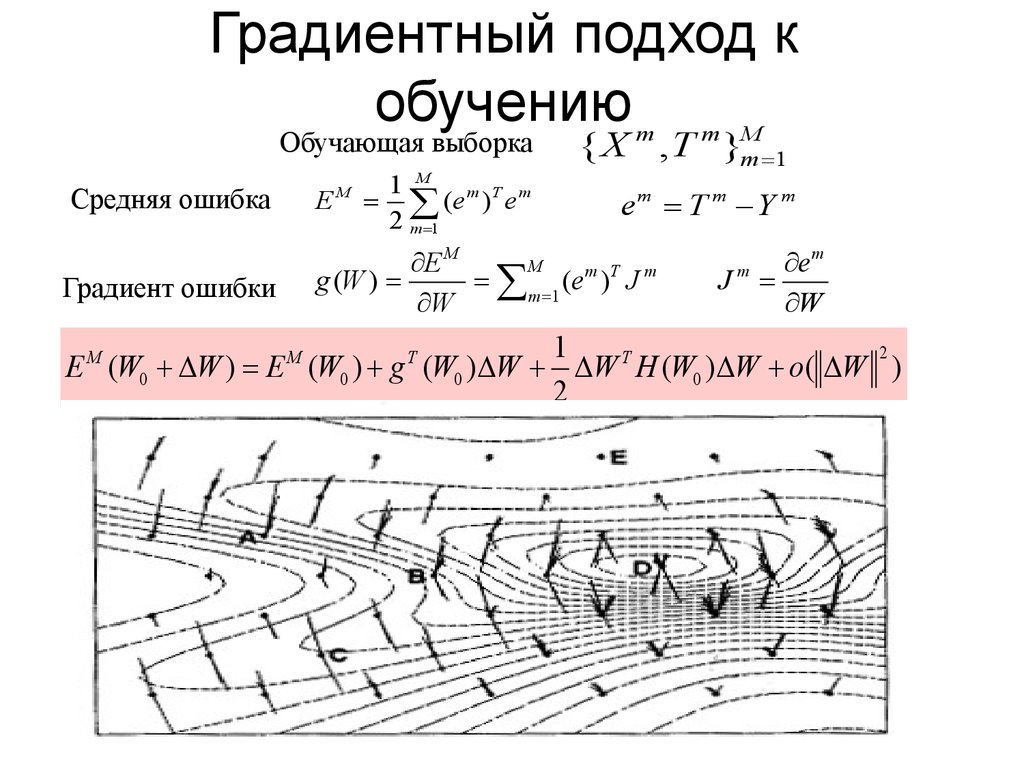
5. Градиентный подход к обучению
Обучающая выборкаСредняя ошибка
E
M
1 M m T m
(e ) e
2 m 1
{ X m , T m }mM 1
em T m Y m
M
E M
g (W )
m 1 (e m )T J m
W
Градиент ошибки
e m
J
W
m
1
2
T
E (W0 W ) E (W0 ) g (W0 ) W W H (W0 ) W o( W )
2
M
M
T
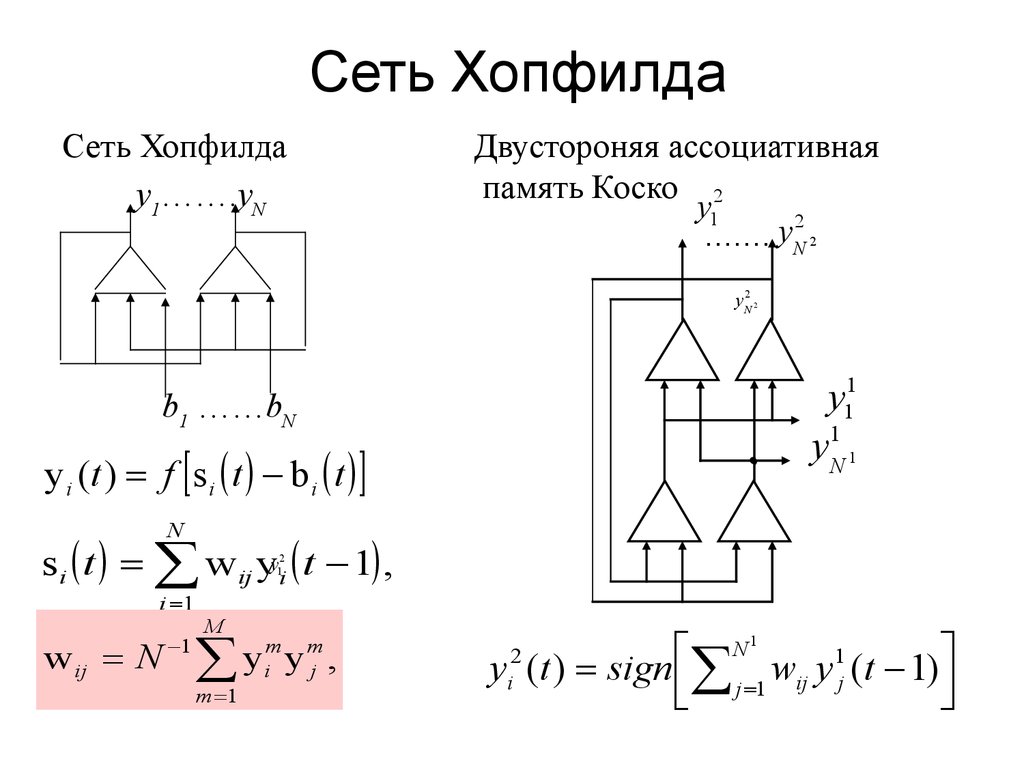
6. Сеть Хопфилда
Сеть Хопфилдаy1…….yN
Двустороняя ассоциативная
память Коско 2
y1
2
y
....... N
2
y N2 2
y11
y1N 1
b1 ……bN
y i (t ) f s i t b i t
N
s i t w ij yyi t 1 ,
2
1
i 1
w ij N
1
M
y
m 1
m
i
m
j
y ,
y (t ) sign j 1 wij y1j (t 1)
2
i
N1
7. Уравнение энергии сети
E(t) - 12 Y T (t)S(t) - 12 Y T (t)WY(t - 1)- 12 Y T (t)W T Y(t 1) 12 Y T (t)[W T Y(t 1)t WY(t - 1)]
E (t ) E (t 1)
H(t -1, t 1)
h 1
E(t )
s h (t 1) Y (t 1)(W - W)Y(t - 1)
T
1
2
T
N
N
N
N
i 1
j 1
i 1 j 1
Inf E(t ) 12 yi (t ) y j (t ) wijE(t) 12 wij
t
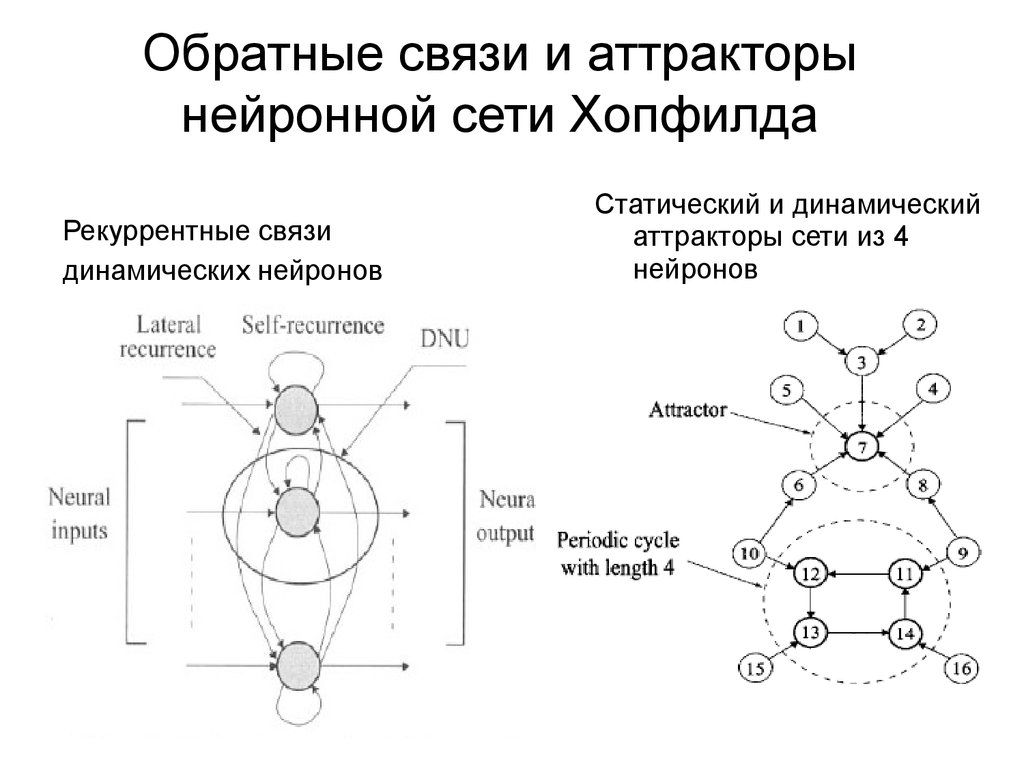
8. Обратные связи и аттракторы нейронной сети Хопфилда
Рекуррентные связидинамических нейронов
Статический и динамический
аттракторы сети из 4
нейронов
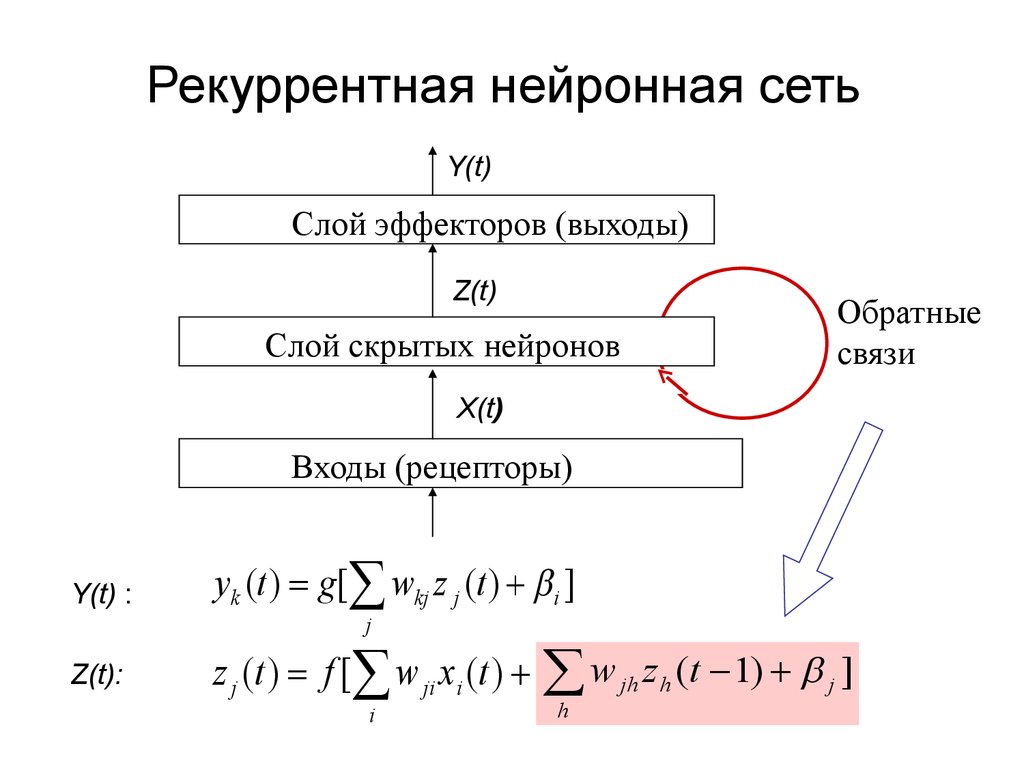
9. Рекуррентная нейронная сеть
Y(t)Слой эффекторов (выходы)
Z(t)
Слой скрытых нейронов
Обратные
связи
X(t)
Входы (рецепторы)
Y(t) :
yk (t ) g[ wkj z j (t ) i ]
j
Z(t):
z j (t ) f [ w ji x i (t ) w jh z h (t 1) j ]
i
h
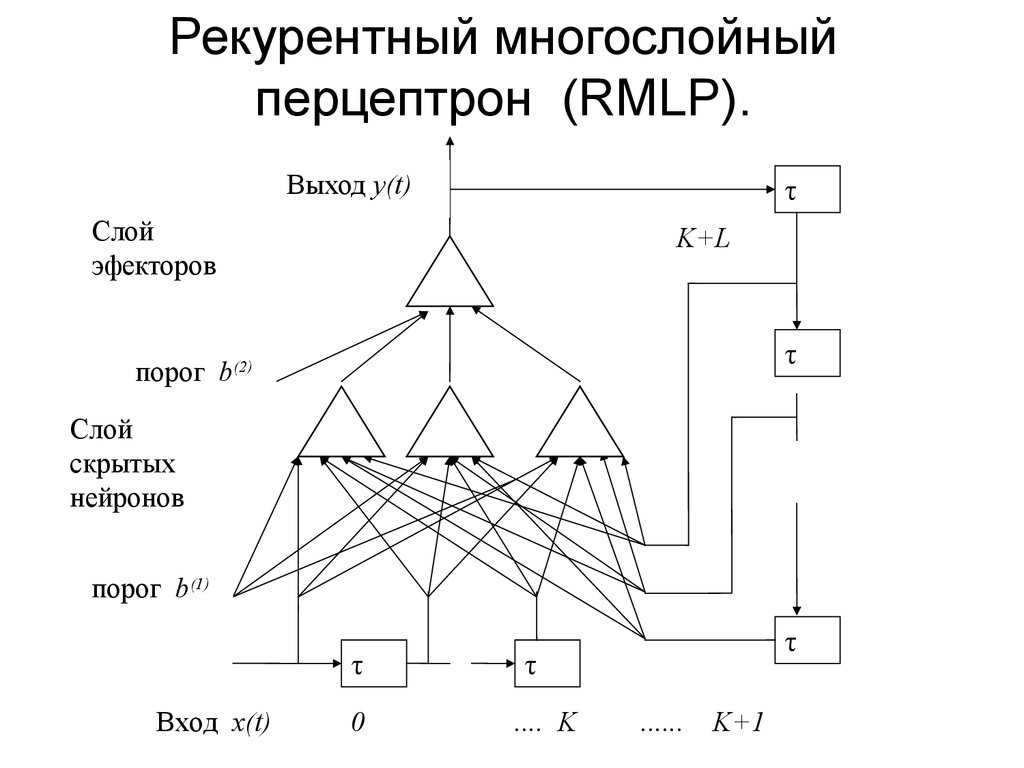
10. Рекурентный многослойный перцептрон (RMLP).
Выход y(t)τ
Слой
эфекторов
K+L
τ
порог b(2)
Слой
скрытых
нейронов
порог b(1)
τ
Вход x(t)
0
τ
τ
.... K
......
K+1
11. Нейроны рекуррентной сети
z (t ) f [ s (t )]l
n
l
n
l
n
s (t ) - постсинаптический потенциал:
l
n
N l 1
s (t ) k l j 1 w z (t ) k 0 w z (t )
l
n
f nl (.)
l
n, j
w
n, j
L
Nk
n, j
l
n, j
k
j
l
l 1
n ,k k
-нелинейная активационная функция нейрона;
-вес связи для j-входа нейрона l-го слоя
-множество значений задержки свзи
Условие устойчивого состояния
z (t ) t ( f s ) s (t ) t 0
l
n
l
n
l
n
l
n
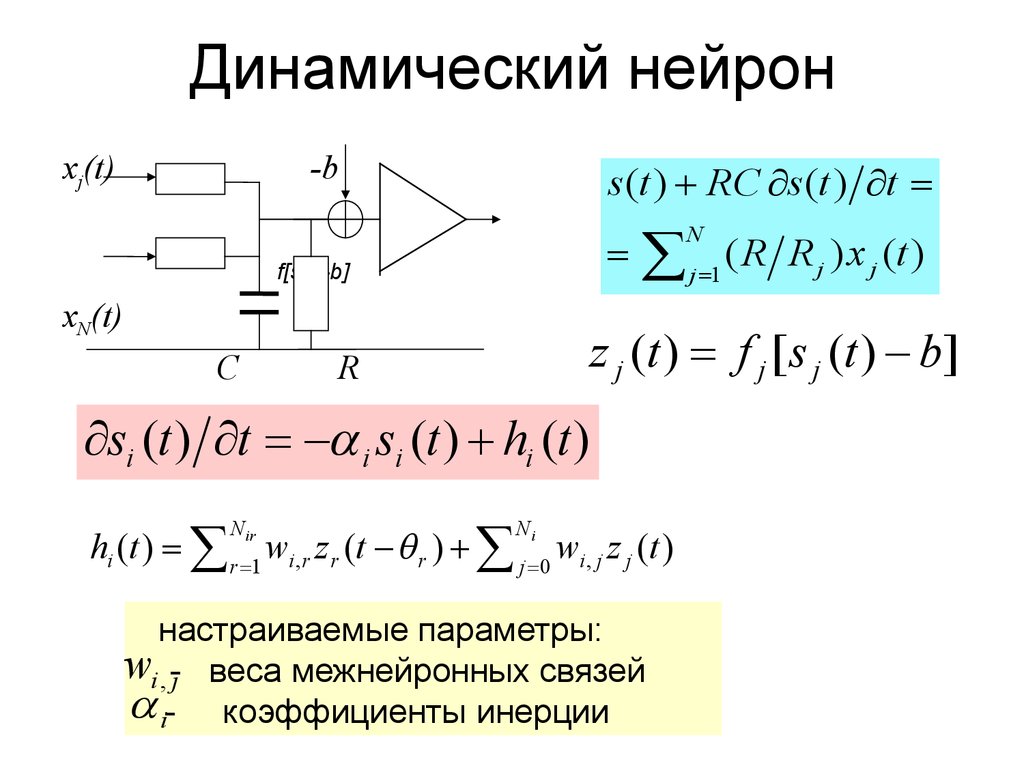
12. Динамический нейрон
xj(t)-b
s (t ) RC s (t ) t
j 1 ( R R j ) x j (t )
N
f[s(t)-b]
xN(t)
si (t ) t i si (t ) hi (t )
C
z j (t ) f j [ s j (t ) b]
R
si (t ) t i si (t ) hi (t )
hi (t ) r 1 wi ,r z r (t r ) j 0 wi , j z j (t )
N ir
Ni
настраиваемые параметры:
wi , -j веса межнейронных связей
i- коэффициенты инерции
13. Обучение рекуррентной нейросети
Функцияошибки
E
Обучающая последовательность
Дельтаправило
(w
X
m
m
L,m 2
(
d
z
m 1 n 1 n n )
NL
M
1
2
,D
m M
;
m 1
(w
l
p , q new
)
m N0
i i 1
l
p , q old
)
m
E w
M
N
E
m
Lm z
m 1 n 1 ( d n z n )
l
w p ,q
z
L
z lp, m
l ,m
p
l ,(m r )
p
z
{
z
m NL
n n 1
X {x } ; D {d }
m
L ,m
n
l ,m
p
для прямых связей
для обратных связей
l
p,q
z
l ,m
p
l
p ,q
w
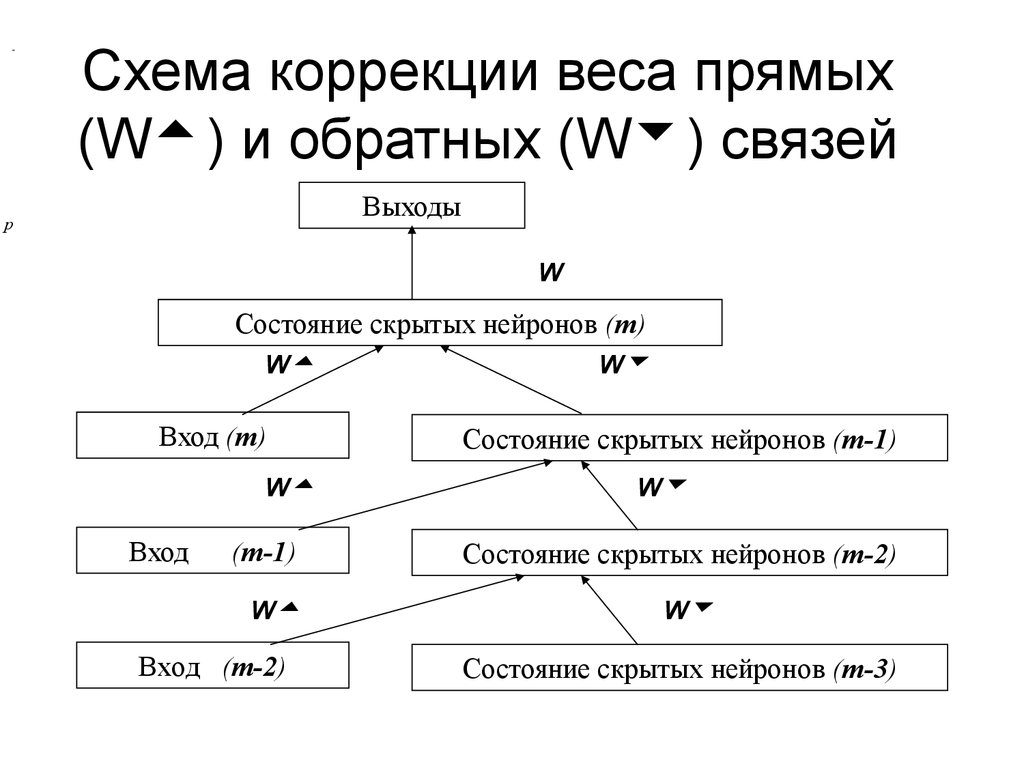
14. Схема коррекции веса прямых (W) и обратных (W) связей
-Схема коррекции веса прямых
(W ) и обратных (W ) связей
Выходы
p
W
Состояние скрытых нейронов (m)
W
Вход (m)
W
Вход
(m-1)
W
Вход (m-2)
W
Состояние скрытых нейронов (m-1)
W
Состояние скрытых нейронов (m-2)
W
Состояние скрытых нейронов (m-3)
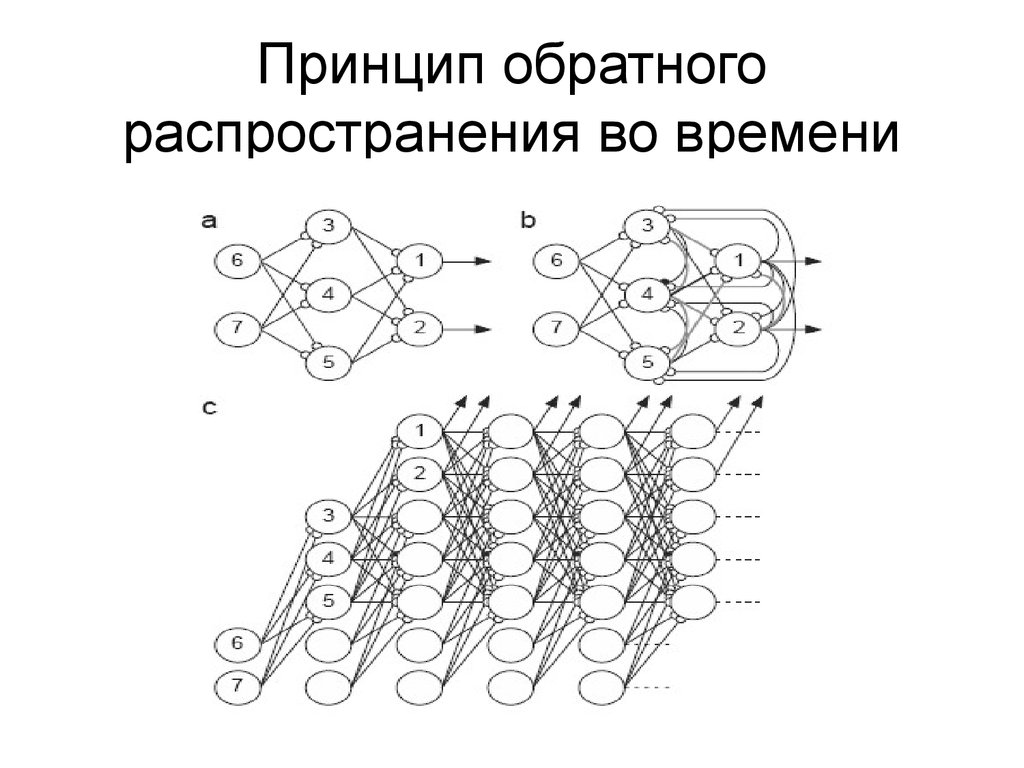
15. Принцип обратного распространения во времени
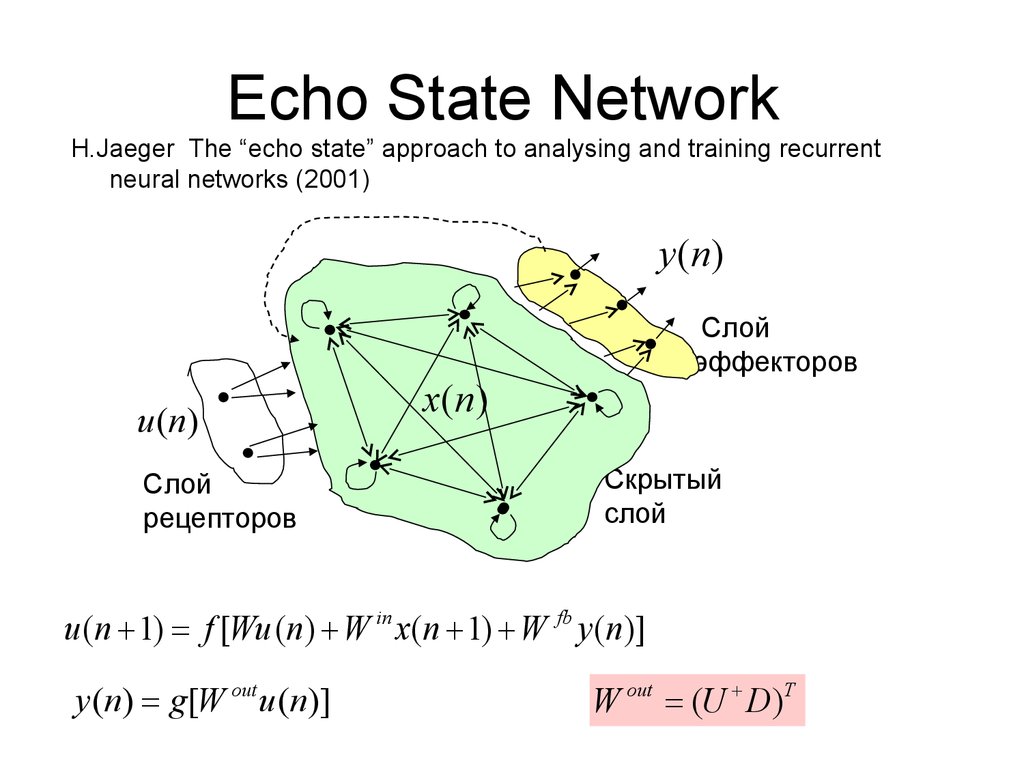
16. Echo State Network
H.Jaeger The “echo state” approach to analysing and training recurrentneural networks (2001)
y (n)
u (n)
Слой
рецепторов
Слой
эффекторов
x(n)
Скрытый
слой
u (n 1) f [Wu (n) W in x(n 1) W fb y (n)]
y (n) g[W out u (n)]
W out (U D)T
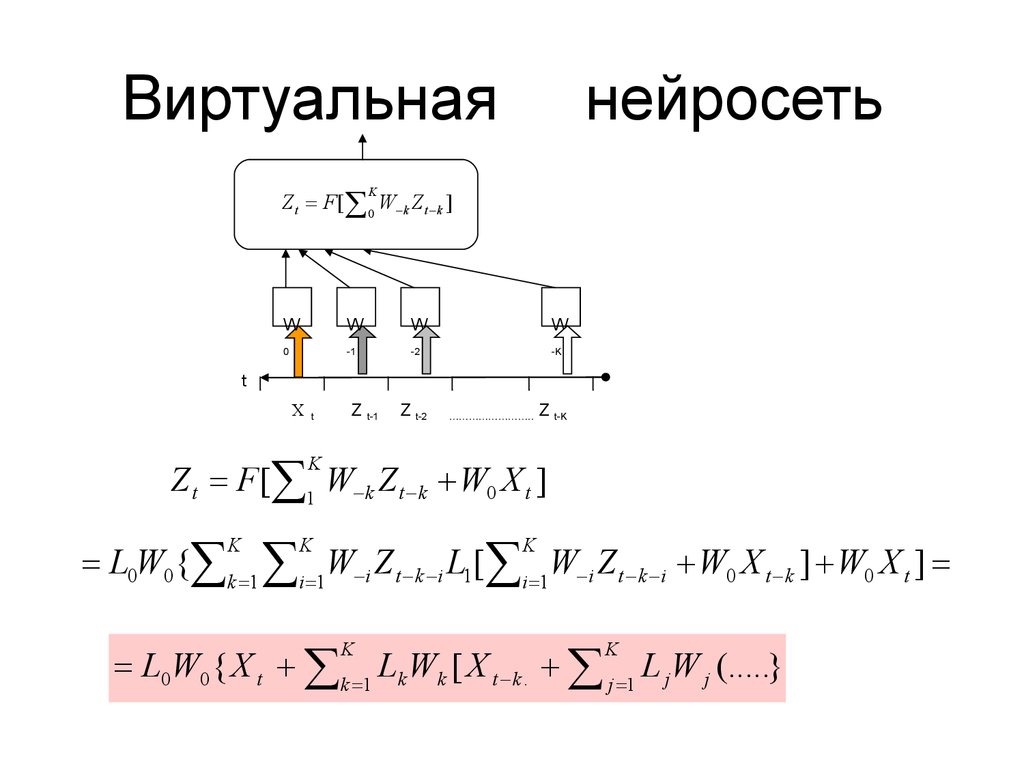
17. Виртуальная нейросеть
Z t F [ 0 W k Z t k ]K
W
W
W
W
0
-1
-2
-K
t
X
t
Z t-1
Z t-2
……………………..
Z t-K
Z t F [ 1 W k Z t k W0 X t ]
K
L0W0 { k 1 i 1W i Z t k i L1[ i 1W i Z t k i W0 X t k ] W0 X t ]
K
K
K
L0W0 { X t k 1 Lk Wk [ X t k . j 1 L j W j (.....}
K
K
18. Уравнение состояния сети
X (t ) InpНейронная сеть как динамическая система (X,Y,U)
U (t ) t F [ U (t ), X (t )]
Y (t ) Out
Y (t ) [U (t )]
U (t ) N
Траектория
состояния
f {U f (t )}Tt0 N T
U (t ) t F [U (t ), X (t )] 0
f
f
f
Условие
аттрактора
____________________________________________________________
Аттракторы
динамической
нейросети
U (t )
t
AU (t ) W Z (t ) 0
Z (t ) F [U (t )] U (t ), 0,
i
1
W A U (t )[U (t )]
f
f
19. Открытая динамическая нейронная сеть
* N*n n 1
Z (t ) {z } ;
*
N * N1 N N 0
Условие аттрактора:
Z * (t ) F ( S * (t )) W * Z * (t ); ii 0
W 11 Z 1 (t ) W 1 Z 1 (t ) W 1 Z 0 (t )
S * (t ) W 1Z 1 (t ) W Z 1 (t ) W 0 Z 0 (t )
Набор динамических атракторов:
1,1
R ...
1,m
R ...
R
1, M
* R1, 0 ... R1,m 1... R1,M 1
0 ,1
R ...
R
0 ,m
....
R
0 ,M
W 01Z 1 (t ) W 0 Z 1 (t ) W 0 Z 0 (t )
* W * *
1
*
W ( )
*
*
20. Псевдоинверсный алгоритм
*m 1i, j
w
m 1
i
s
w (ri
*m
i, j
m 1
m 1
i
s
k 1 w r
N*
*m m 1
ik k
Свойства матрицы
d
m 1
)(r
m 1
j
s
r
N*
m 1
j
) d
m 1 m 1
k
k 1 ik
(r
s
m 1
m 1
k
)
*
W ( )
*
*
w j 1 ( wi*, j ) 2
W (W ) ;
TrW i 1 w M ;
M
w *;
N
M M
M
M
* 2
1 * ( wi , j ) * *
1 * , i j
*
N N
N ( N 1) N
*
*
i ,i
* 2
*
N*
*
i ,i
*
i ,i
N*
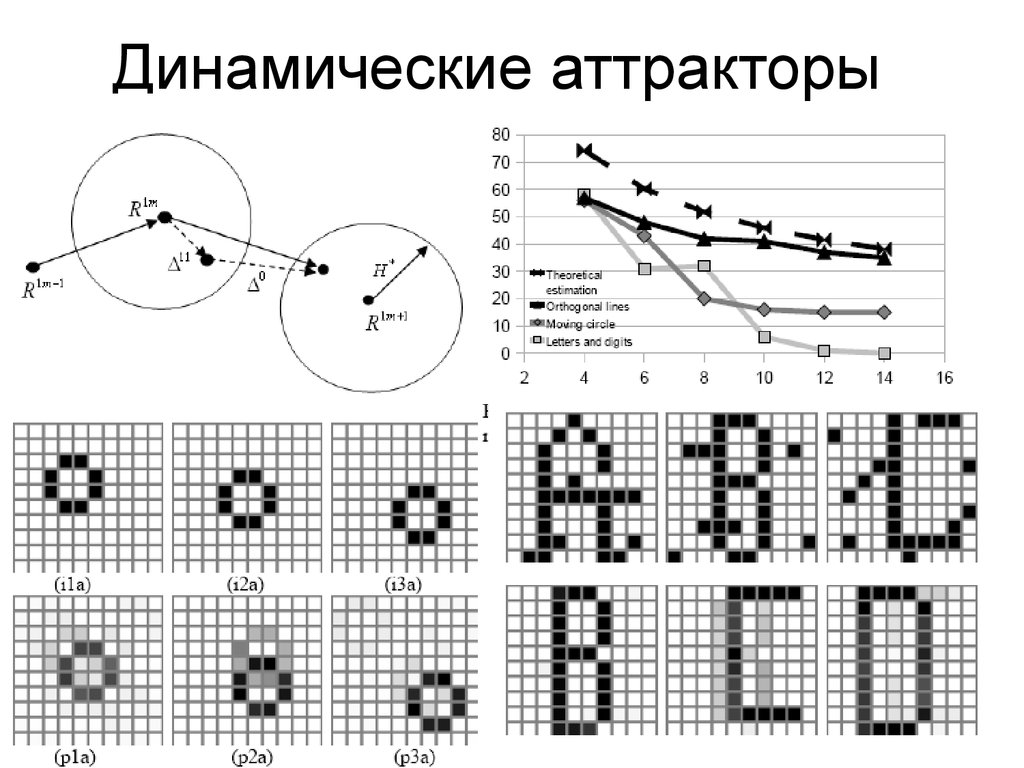
21. Динамические аттракторы
22. Фрагмент нервной ткани коры мозга
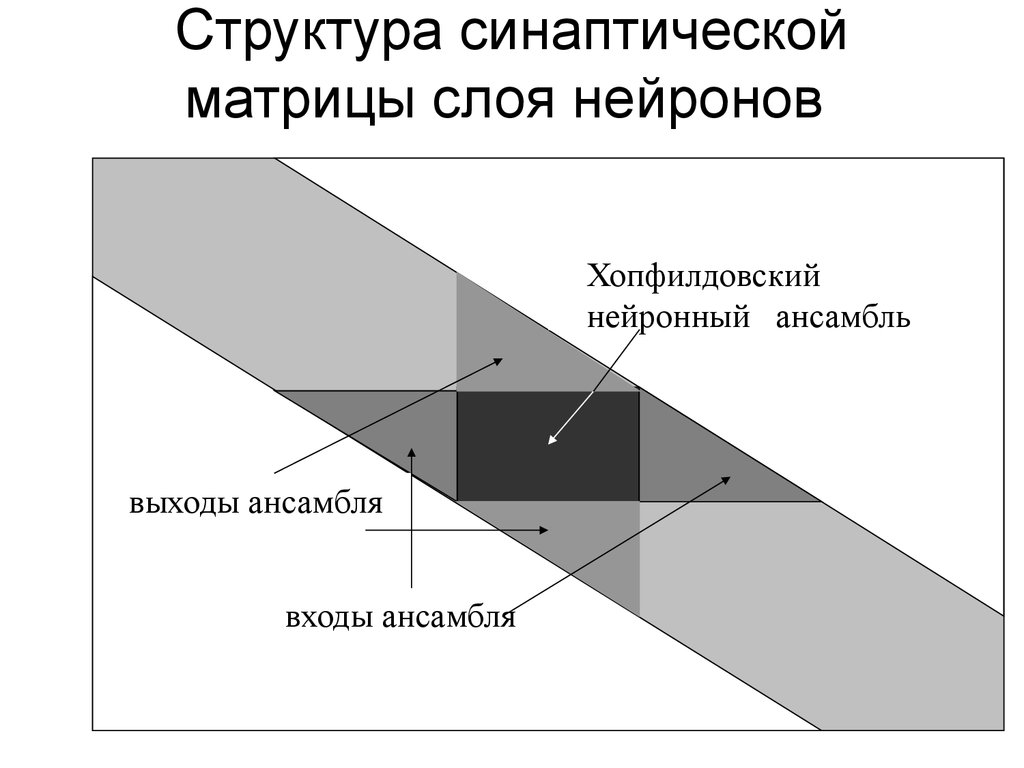
23. Структура синаптической матрицы слоя нейронов
Хопфилдовскийнейронный ансамбль
выходы ансамбля
входы ансамбля







 mathematics
mathematics informatics
informatics








