Нейронные сети. Введение

1. Нейронные сети Введение

Корлякова М.О.
2019

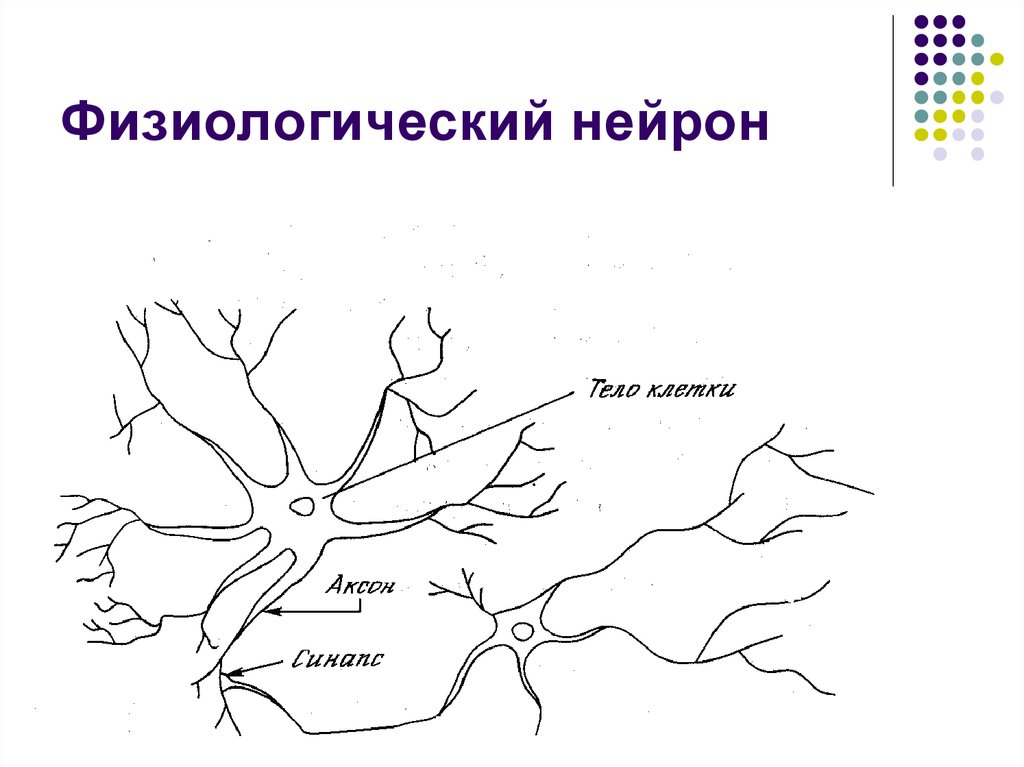
2. Физиологический нейрон

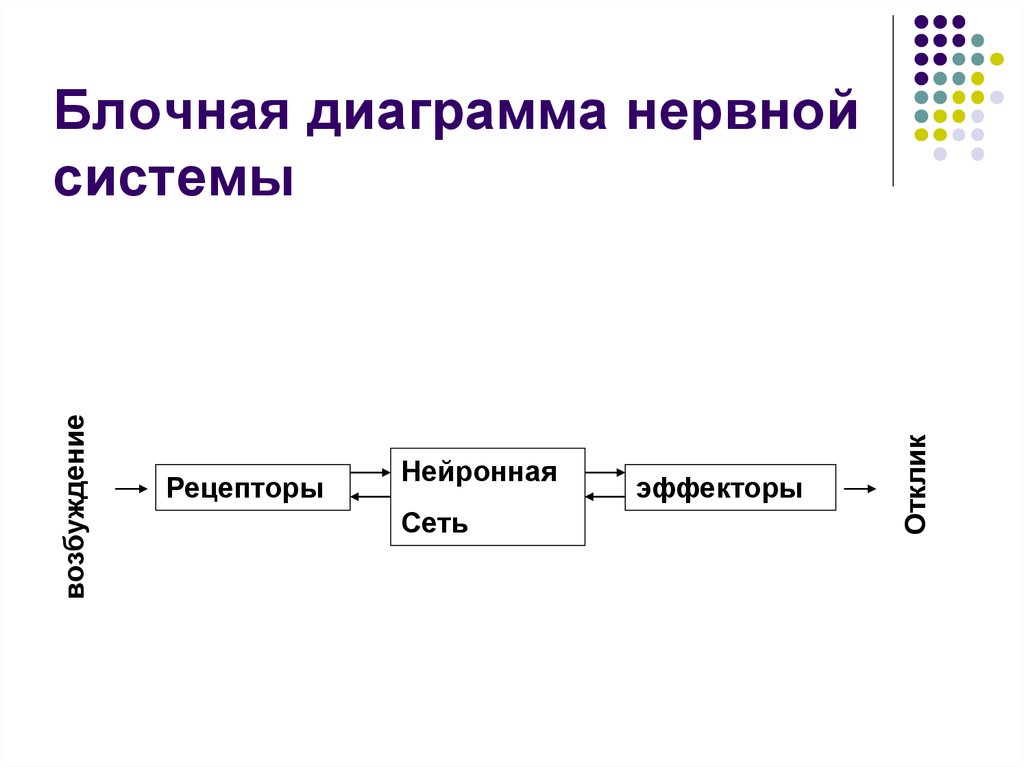
3. Блочная диаграмма нервной системы

Рецепторы
Нейронная
Сеть
эффекторы
Отклик
возбуждение
Блочная диаграмма нервной
системы

4.

1942 – Мак-Каллок – Питц
1948 – Н.Винер – «Кибернетика»
1949 – Хебб
1949 – Аттли - обученная нейросеть
1960 – алгоритм обучения по наименьшим
квадратам (Least mean-square - LMS)
1960-1970 – Розенблат – обучение
перцептрона
1969 – Минский – Пайперт –
фундаментальное ограничение линейных
нейросетей.

5.

1967 – Кован – сигмоидальная функция
1980 – Теория Адаптивного Резонанса –
АRТ
1970-1980 – самоорганизация – Карты
Кохонена
1980 – Гросберг – конкурентное обучение
1982 – Хопфилд – функция энергии для
описания рекуррентных сетей
1986 – Алгоритм обратного
распространения по ошибке

6. Нейроны

Хебба
Маккалока – Питца
Сигмоидный
Гросберга
Радиальный
WTA

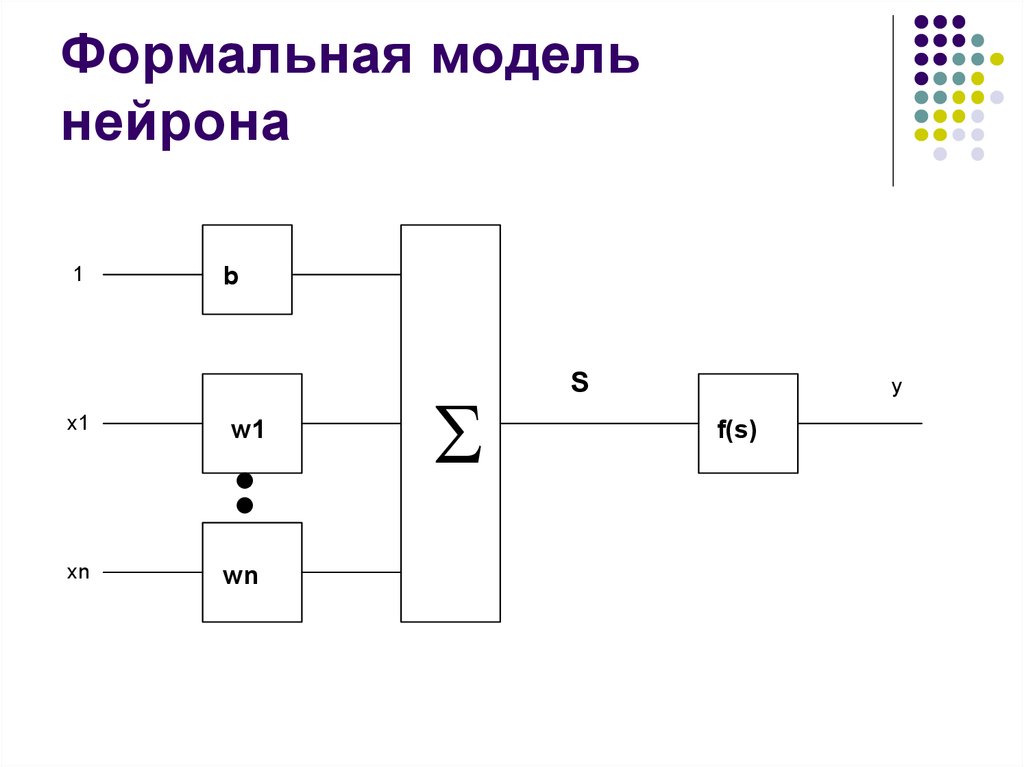
7. Формальная модель нейрона

1
bа0
x1
а1
w1
xn
аn
wn
SNET
y
f(y)
f(s)

8. Формальная модель нейрона

n
y= f(S)= f( е
wi x i + b)
i= 1

9. Активационные функции

Линейные.
Нелинейные.

10. Модель нейрона Мак-Калока – Питца

y
y
S
S
(-1,1)
(0,1)

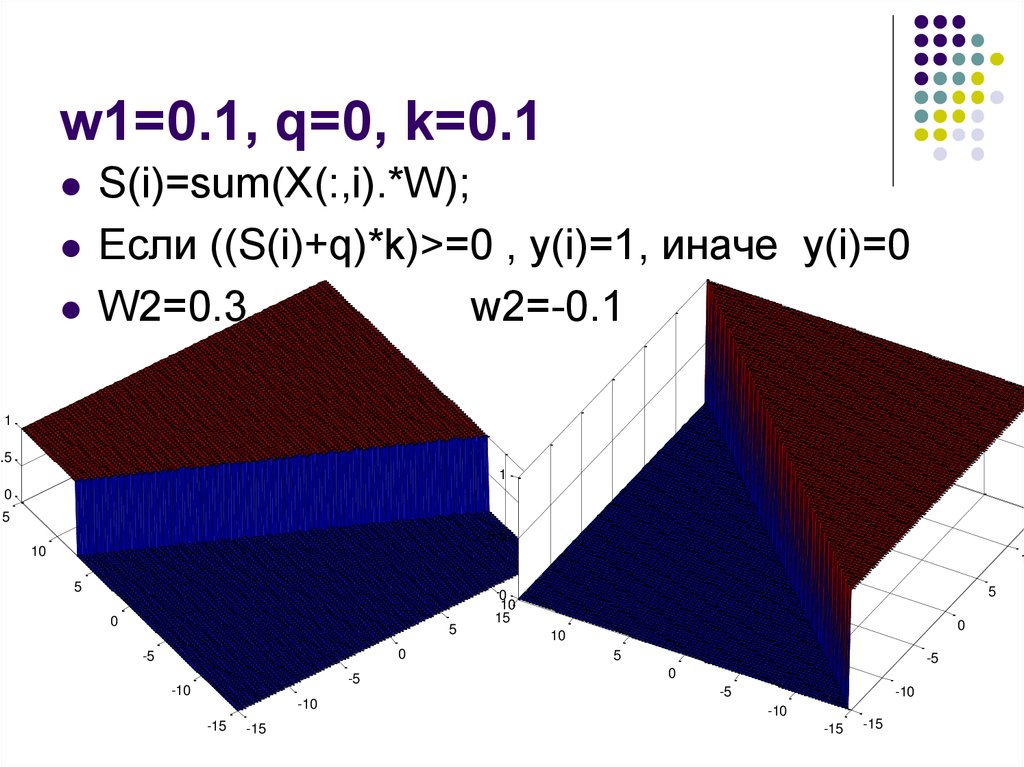
11. w1=0.1, q=0, k=0.1

S(i)=sum(X(:,i).*W);
Если ((S(i)+q)*k)>=0 , y(i)=1, иначе y(i)=0
W2=0.3
w2=-0.1
1
0.5
1
0
15
0.5
10
1
15
5
0
5
0
-5
-5
-10
-10
-15
-15
5
0
10
15
0
10
5
-5
0
-5
-10
-10
-15
-15

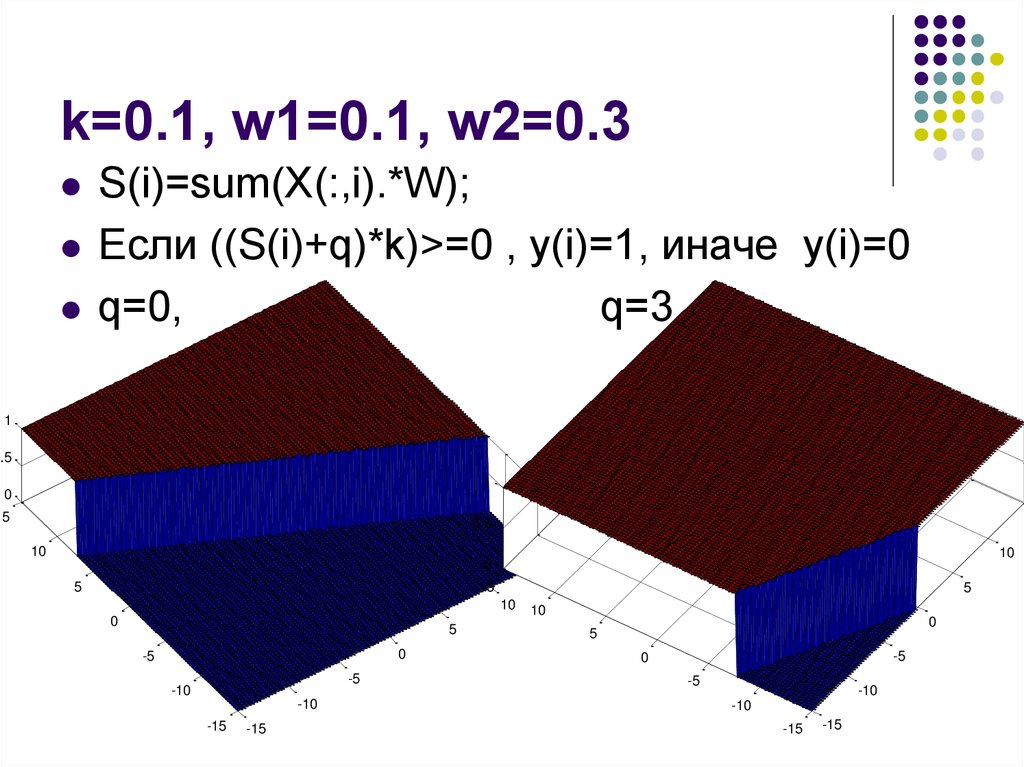
12. k=0.1, w1=0.1, w2=0.3

S(i)=sum(X(:,i).*W);
Если ((S(i)+q)*k)>=0 , y(i)=1, иначе y(i)=0
q=0,
q=3
1
0.5
1
0
15
0.5
10
10
0
5
15
15
10
0
5
0
-5
-5
-10
-10
-15
-15
5
10
0
5
-5
0
-5
-10
-10
-15
-15

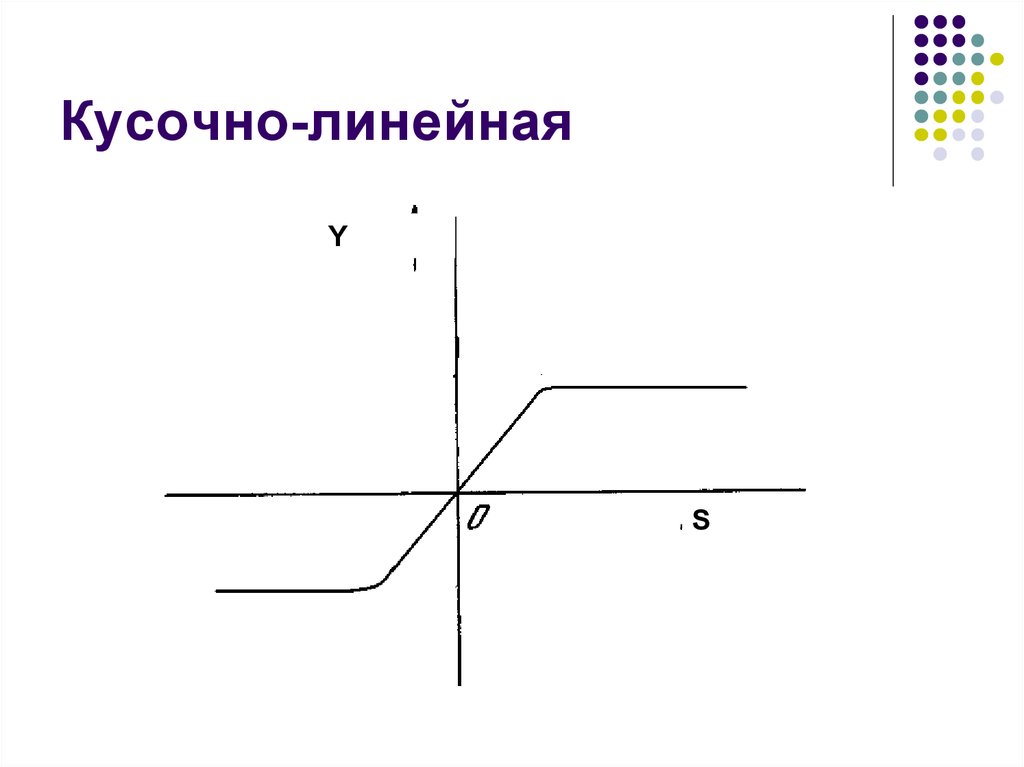
13. Кусочно-линейная

Y
S

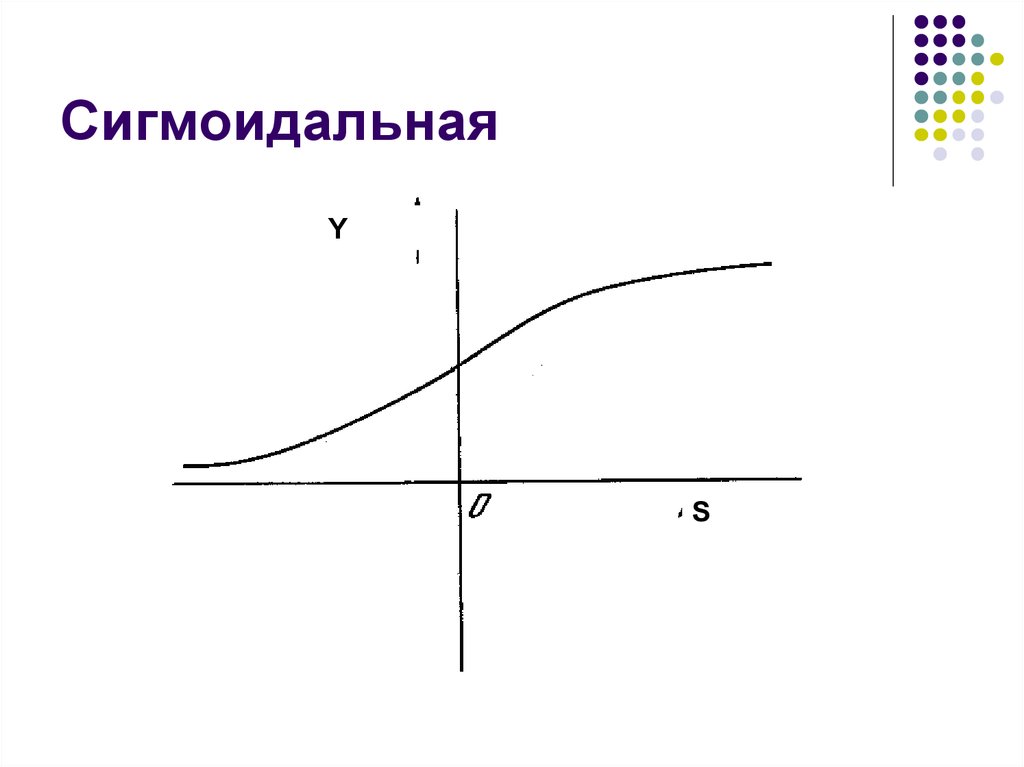
14. Сигмоидальная

Y
S

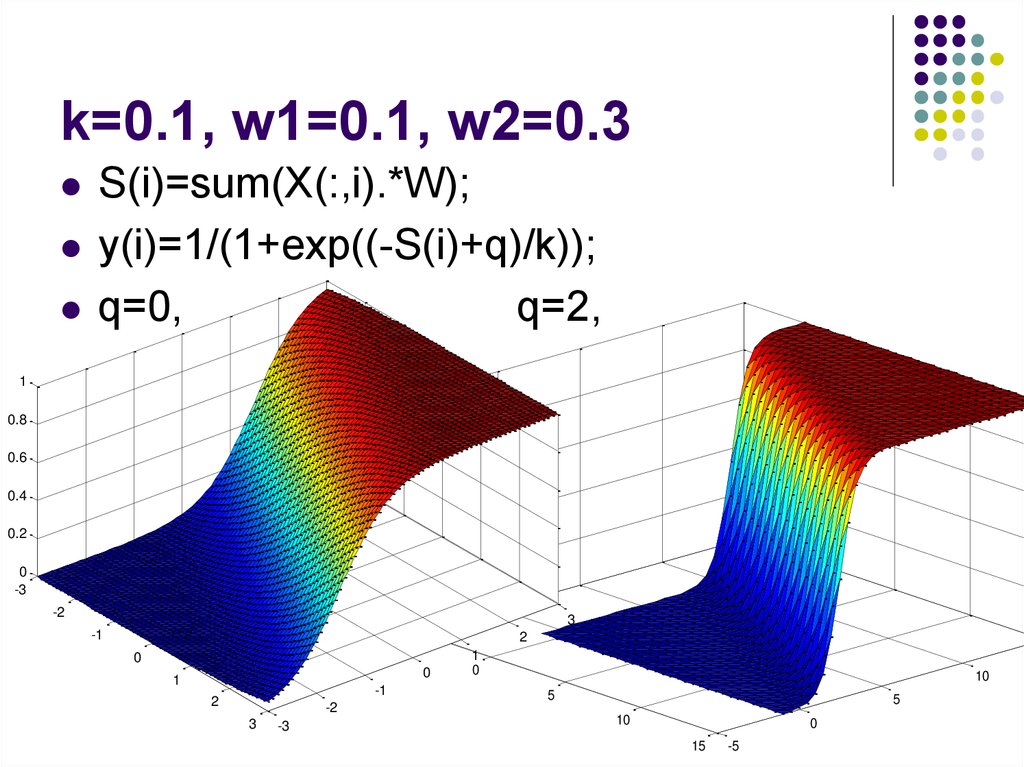
15. k=0.1, w1=0.1, w2=0.3

S(i)=sum(X(:,i).*W);
y(i)=1/(1+exp((-S(i)+q)/k));
q=0,
q=2,
1
1
0.8
0.8
0.6
0.6
0.4
0.2
0.4
0
-3
0.2
-2
3
0
-5
-1
2
0
0
1
-1
2
-2
3
-3
1
0
10
5
5
10
0
15
-5

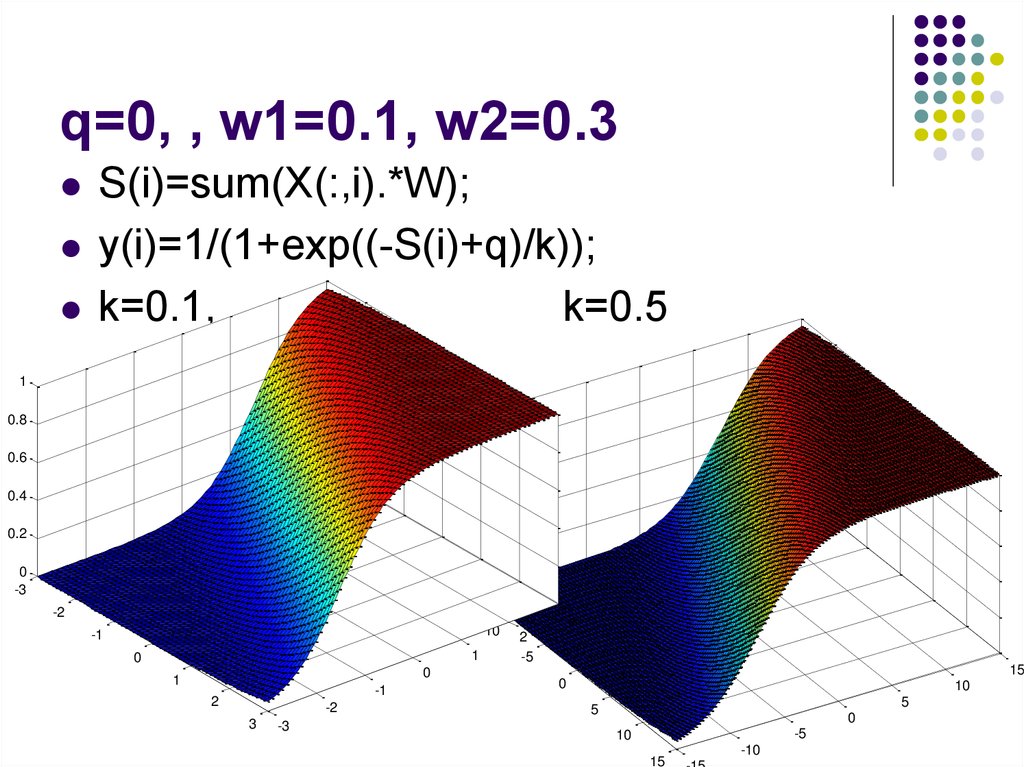
16. q=0, , w1=0.1, w2=0.3

S(i)=sum(X(:,i).*W);
y(i)=1/(1+exp((-S(i)+q)/k));
k=0.1,
k=0.5
1
1
0.8
0.8
0.6
0.6
0.4
0.4
0.2
0.2
0
-3
0
-15
-2
-10
-1
1
0
0
1
-1
2
-2
3
-3
3
2
-5
15
0
10
5
5
0
-5
10
15
-10

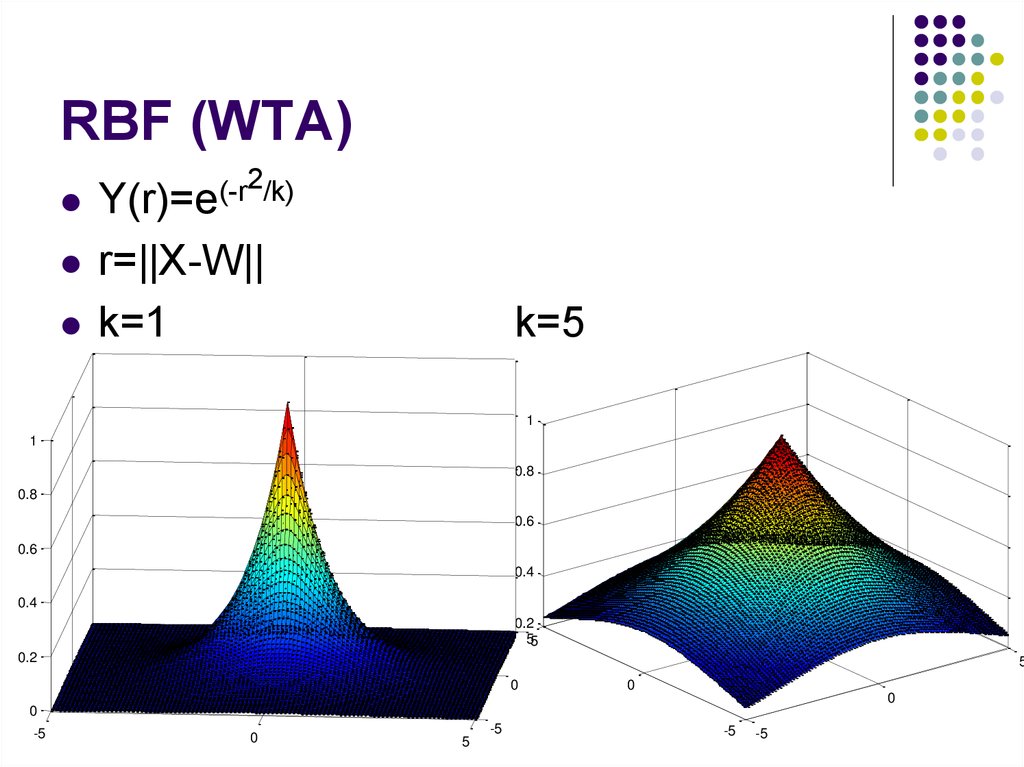
17. RBF (WTA)

2/k)
(-r
Y(r)=e
r=||X-W||
k=1
k=5
1
1
0.8
0.8
0.6
0.6
0.4
0.4
0.2
55
0.2
5
0
0
0
0
-5
0
5
-5
-5
-5

18. Нейронная сеть

Число слоев/число нейронов по слоям
Обратные связи
Активационные функции
Число входов
Число выходов
Алгоритм настройки весов(обучения)
Тип задачи, решаемой сетью

19. Слой нейросети

Группа нейронов сети:
Общие функции (задачи)
Общие внешние связи
Общие входы
Зачем выделять слой?

20. Режимы функционирования нейросетей

Обучение
Работа

21. Формальная модель сети

f(X)=Net(X)

22. Архитектуры НС (классификация)

Тип обучения
Класс алгоритмов оучения
Число слоев:
С учителем
Без учителя
Однослойные
многослойные.
Обратные связи:
Нет – сети прямого распространения
Есть – рекуррентные сети.

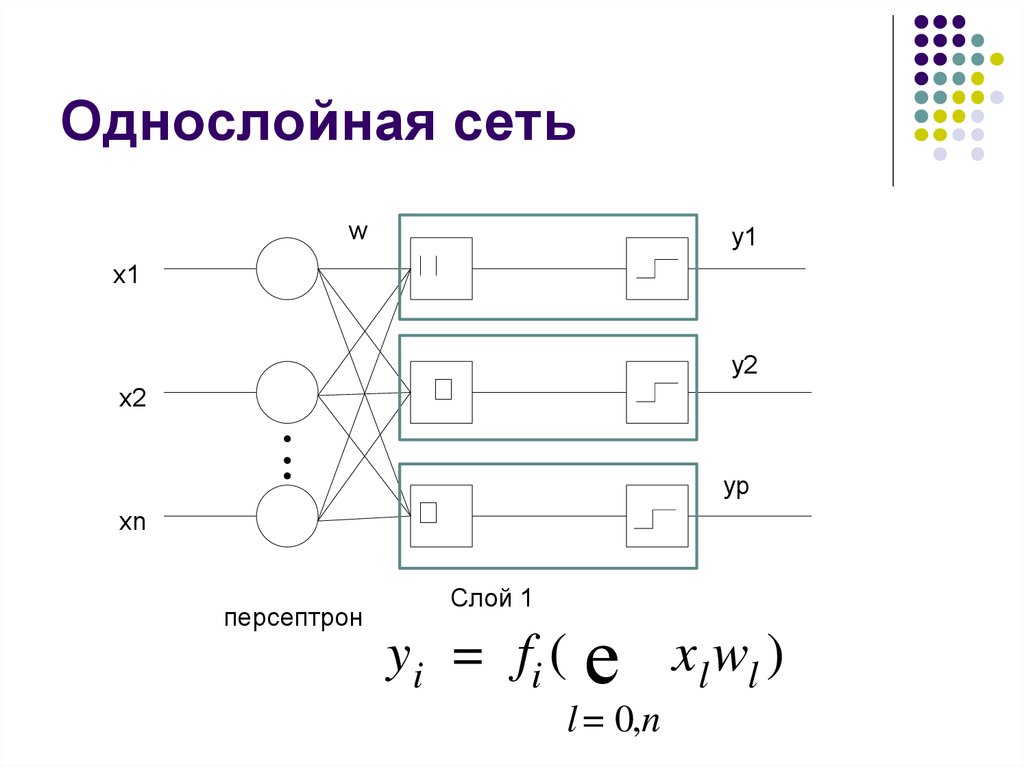
23. Однослойная сеть

w
y1
OUT1
x1
y2OUT2
x2
yp OUTn
xn
персептрон
Слой 1
y i = fi (
е
l = 0,n
x l wl )

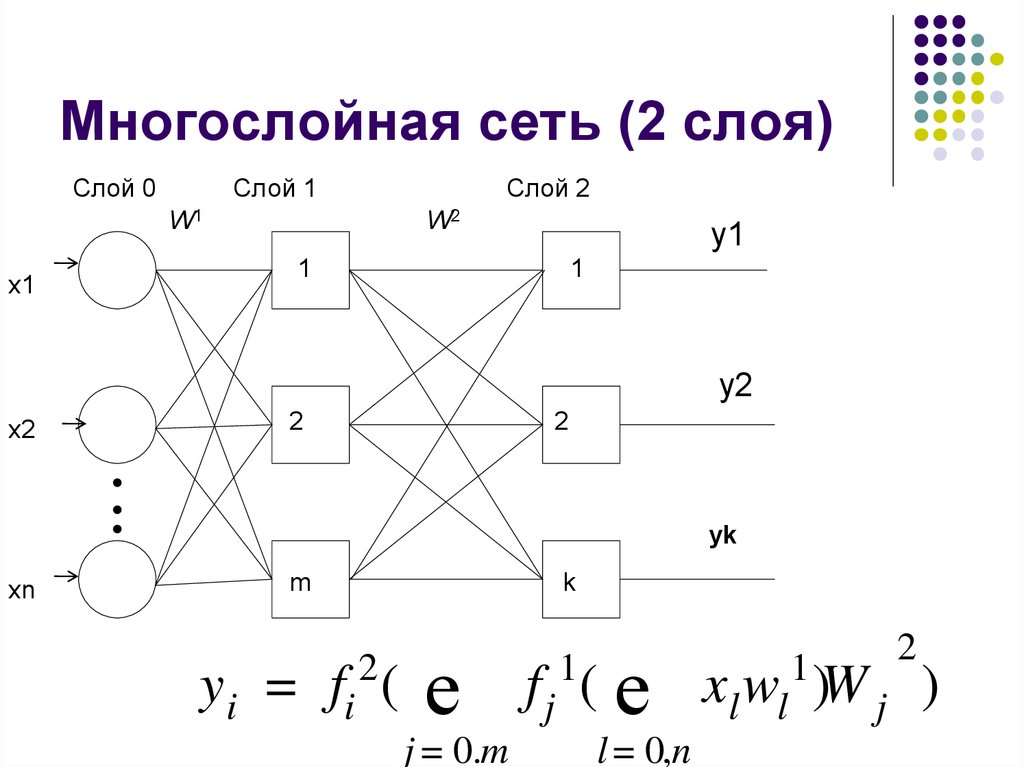
24. Многослойная сеть (2 слоя)

Слой 0
Слой 1
W2к
W1w
x1
Слой 2
y1
1
1
y2
x2
2
2
yk
y
xn
m
k
2
yi = fi (
е
j = 0.m
2
f j ( е xl wl )W j )
1
1
l = 0,n

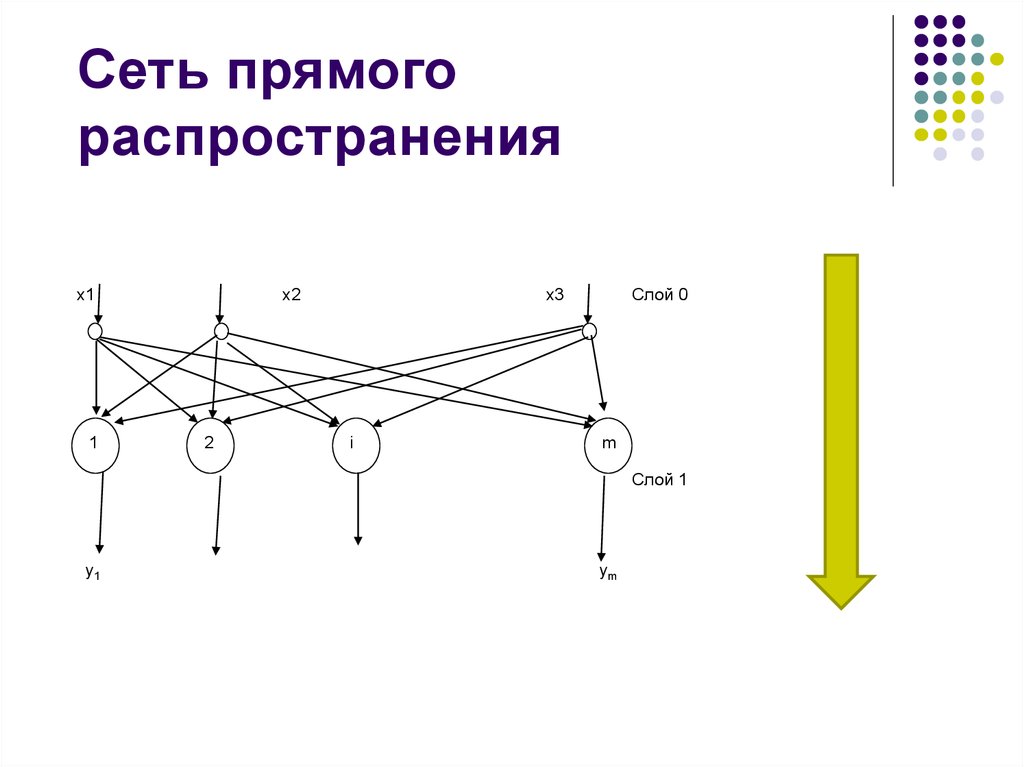
25. Сеть прямого распространения

x1
1
x2
2
Слой 0
x3
i
m
Слой 1
y1
ym

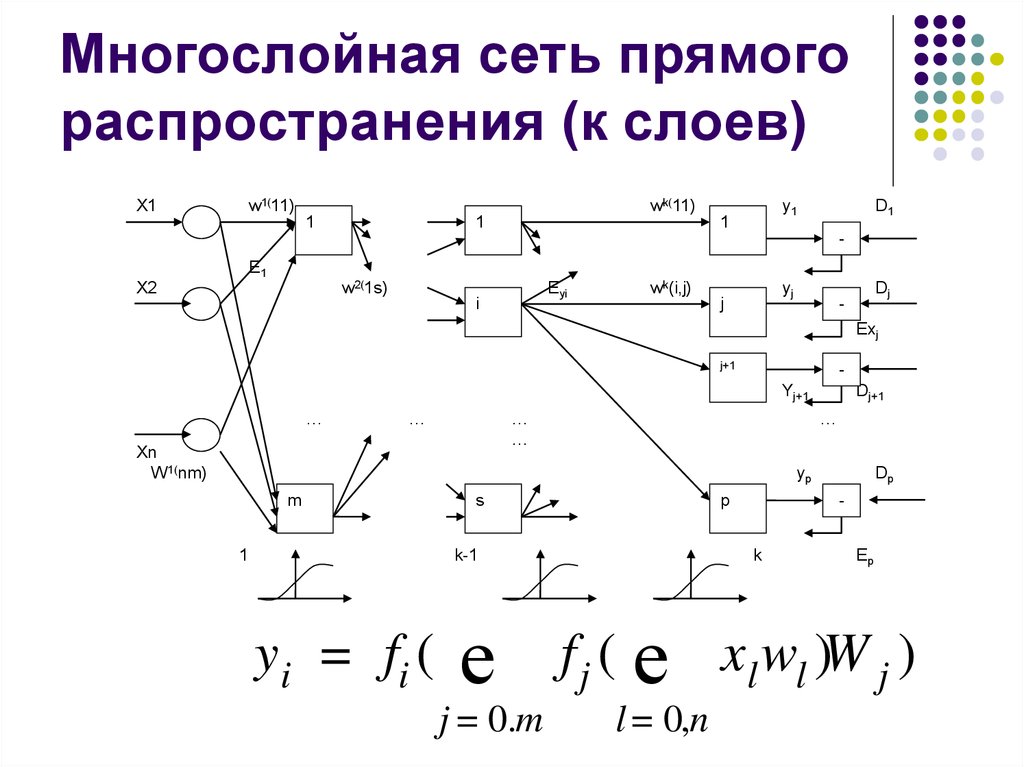
26. Многослойная сеть прямого распространения (к слоев)

w1(11)
X1
wk(11)
1
1
y1
1
D1
-
E1
w2(1s)
X2
Eyi
i
wk(i,j)
yj
j
Dj
-
Exj
j+1
Yj+1
…
…
…
…
Xn
W 1(nm)
Dj+1
…
yp
m
1
s
p
k-1
y i = fi (
е
j = 0.m
Dp
-
k
Ep
f j ( е xl wl )W j )
l = 0,n

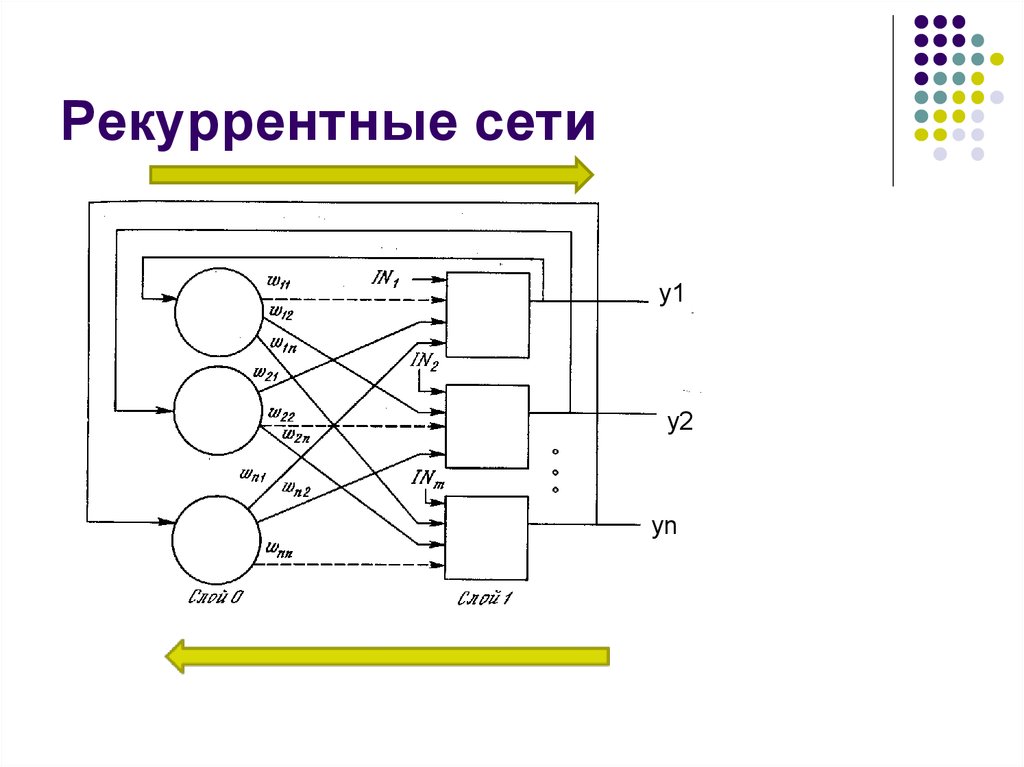
27. Рекуррентные сети

y1
y2
yn

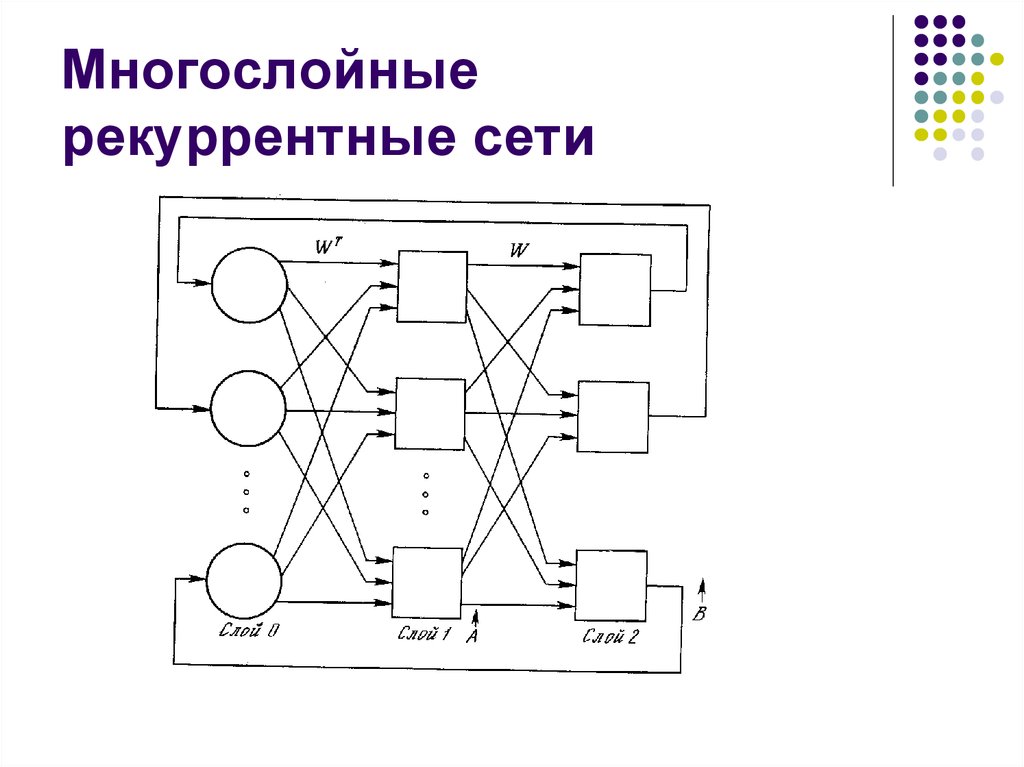
28. Многослойные рекуррентные сети

29. Виды обучения

С учителем
T={(Xi,di)}, i=1,N
Xi- входной вектор
di – выходной вектор
Без учителя
T={Xi}, i=1,N
Xi- входной вектор

30. Классы алгоритмов обучения нейронных сетей

wkj
«Правило Хебба»
Коррекция по ошибке
e y X i di
Стохастическое
обучение
1
E wkj xk x j
2 j k ( j k )
«Правило
соревнования» –
конкурентное
обучение
wkj xi wkj , 0

31. Вселенский разум

32. Вопрос

Вариант 1
Вычислить реакцию
порогового нейрона с
W=[ 1 ,-1] на входное
воздействие Х=[0 ,1] c
порогом Θ=0
Вариант 3
Вычислить реакцию
линейного нейрона с
W=[ -1 ,-1] на входное
воздействие Х=[0 ,1] c
порогом Θ=0 и наклоном
k=1
Вариант 2
Вычислить реакцию
сигмоидного нейрона с
W=[ -1 ,1] на входное
воздействие Х=[1 ,1] c
порогом Θ=0 и наклоном
k=1
Вариант 4
Вычислить реакцию
радиального нейрона с
W=[ 1 , 1] на входное
воздействие Х=[0 ,1] c
радиусом k=1

33. литература

Комарцова Л.Г. Максимов А.В.
Нейрокомпьютеры – М.:Из-во МГТУ 2004.

34. Темы рефератов

Критика моделей искусственного
интеллекта предложенных в НФ
литературе
Модели формальных нейронов (не МакКалока-Питца): их достоинства и
недостатки.
Модель обучения по Дельта-правилу:
исследовать ограничения и возможнсти.