Similar presentations:
Нейронные сети. Лекция 3+
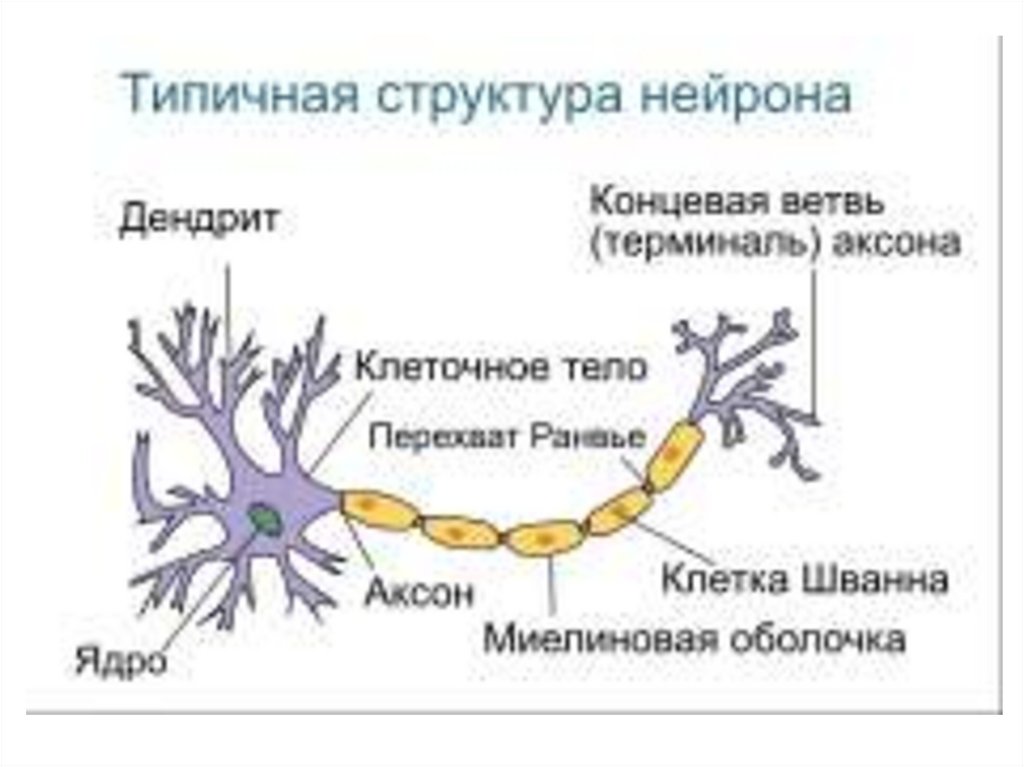
1. Нейронные сети
2.
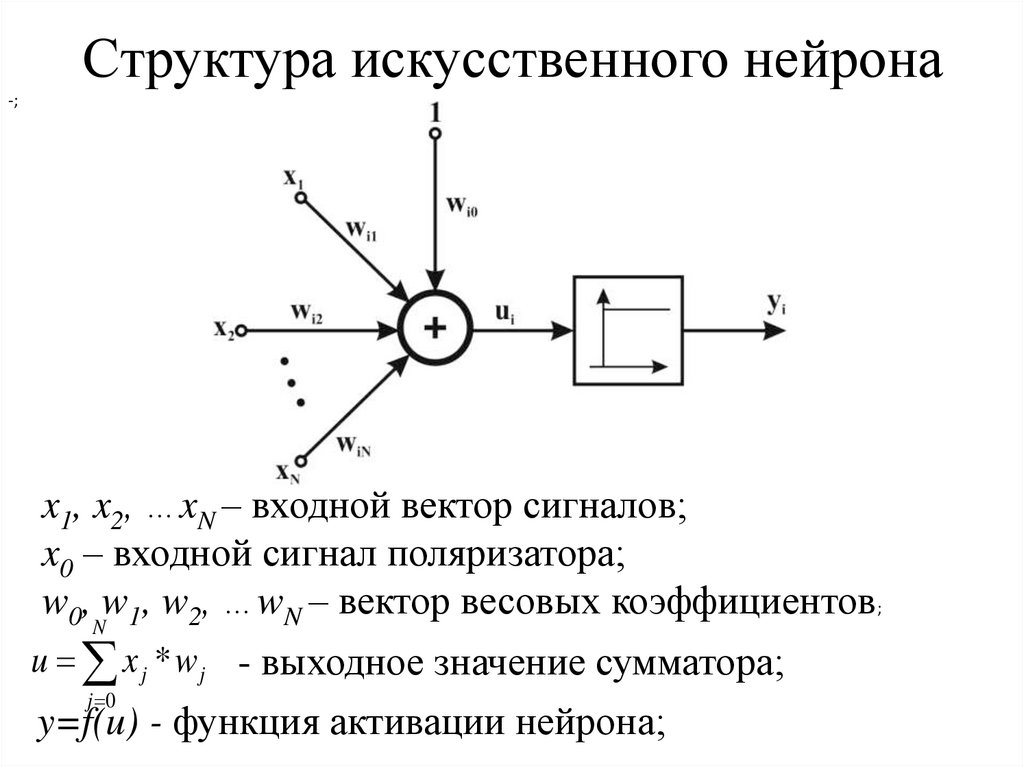
3. Структура искусственного нейрона
-;x1, x2, …xN – входной вектор сигналов;
x0 – входной сигнал поляризатора;
w0, w1, w2, …wN – вектор весовых коэффициентов;
N
u x j * w j - выходное значение сумматора;
j 0
y=f(u) - функция активации нейрона;
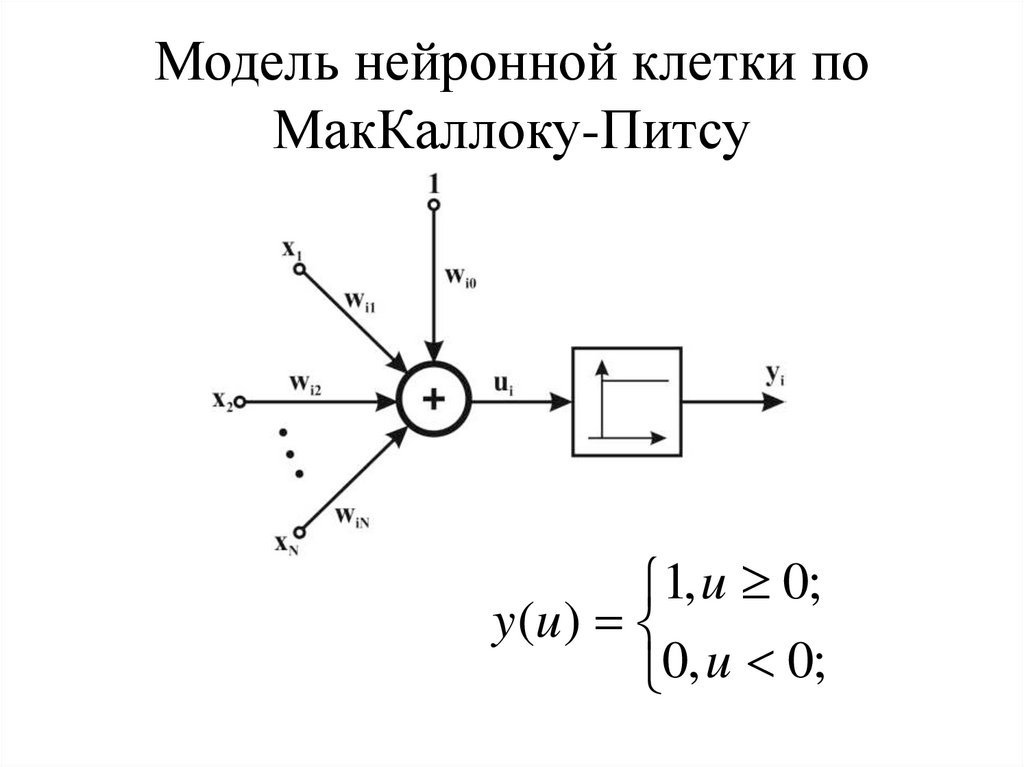
4. Модель нейронной клетки по МакКаллоку-Питсу
1, u 0;y (u )
0, u 0;
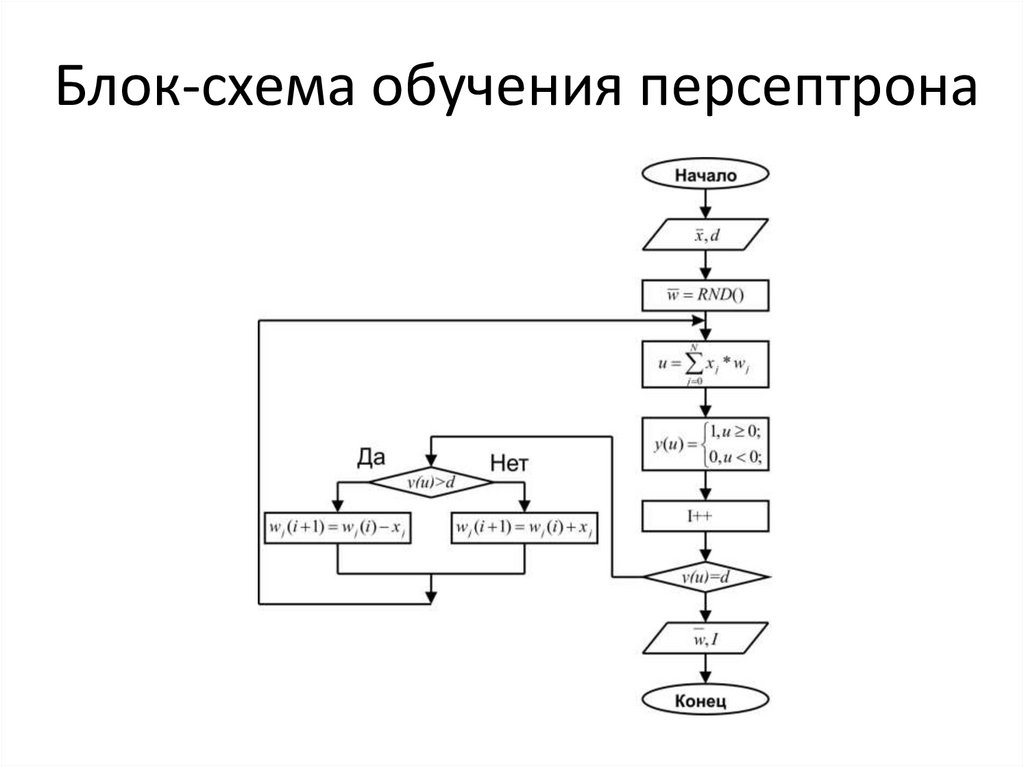
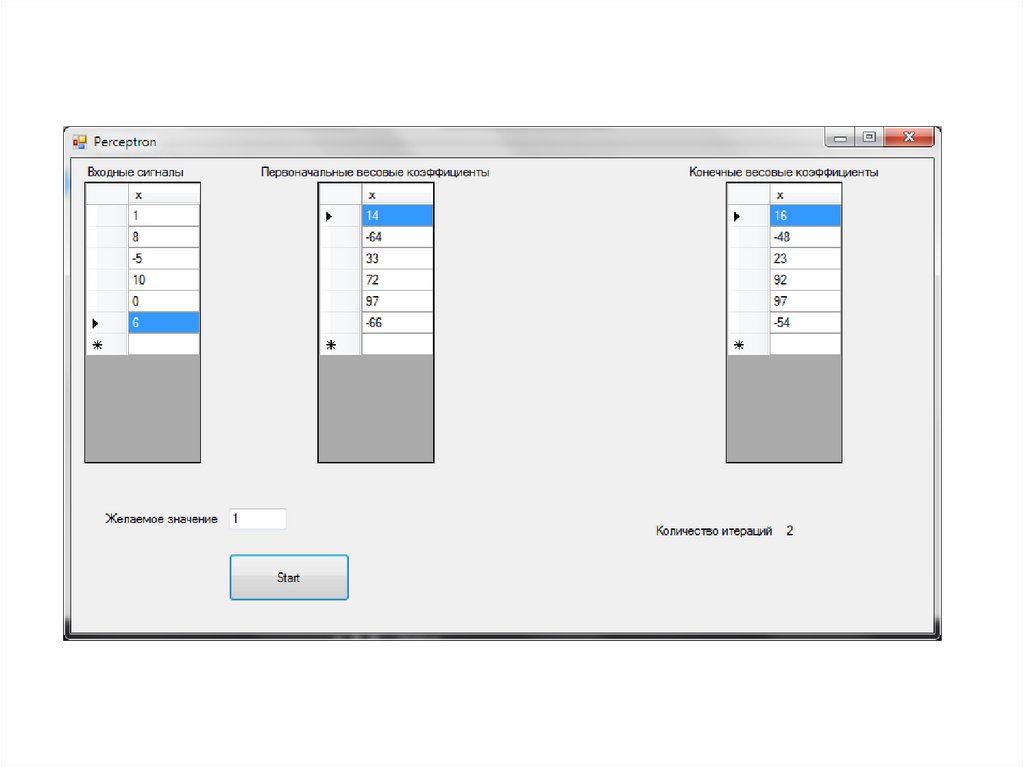
5. Блок-схема обучения персептрона
6.
7. Правило Видроу-Хоффа
wi j (t 1) wi j (i ) wij ;wij x j (d i yi );
8.
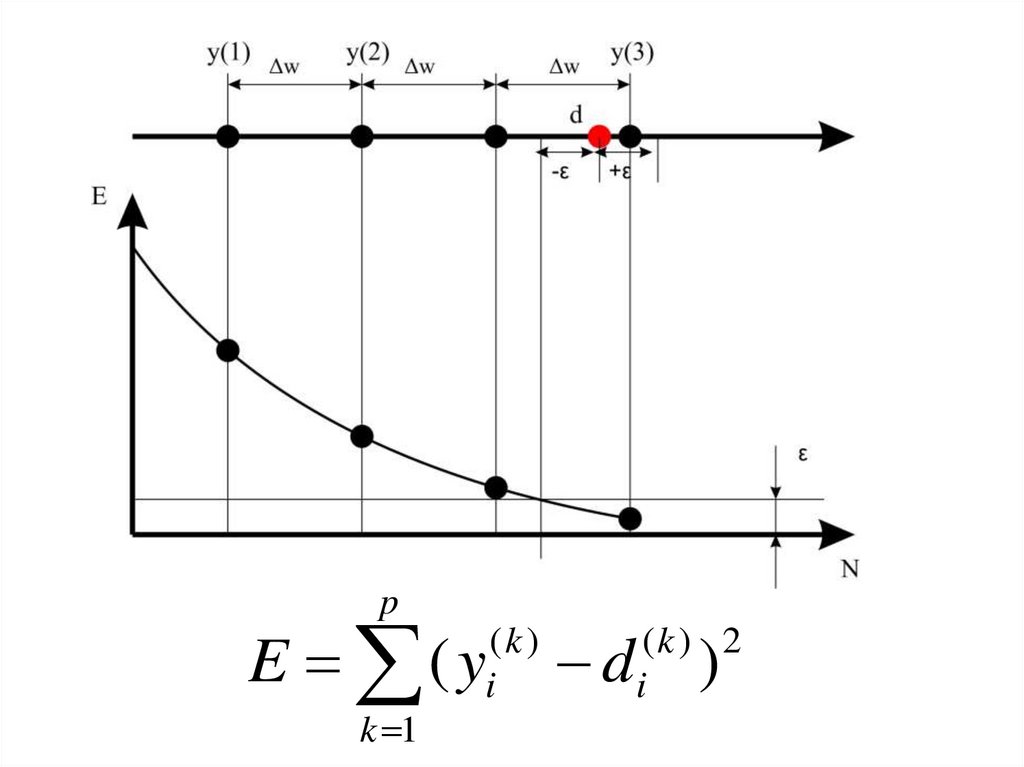
pE ( y
k 1
(k )
i
d
(k ) 2
i
)
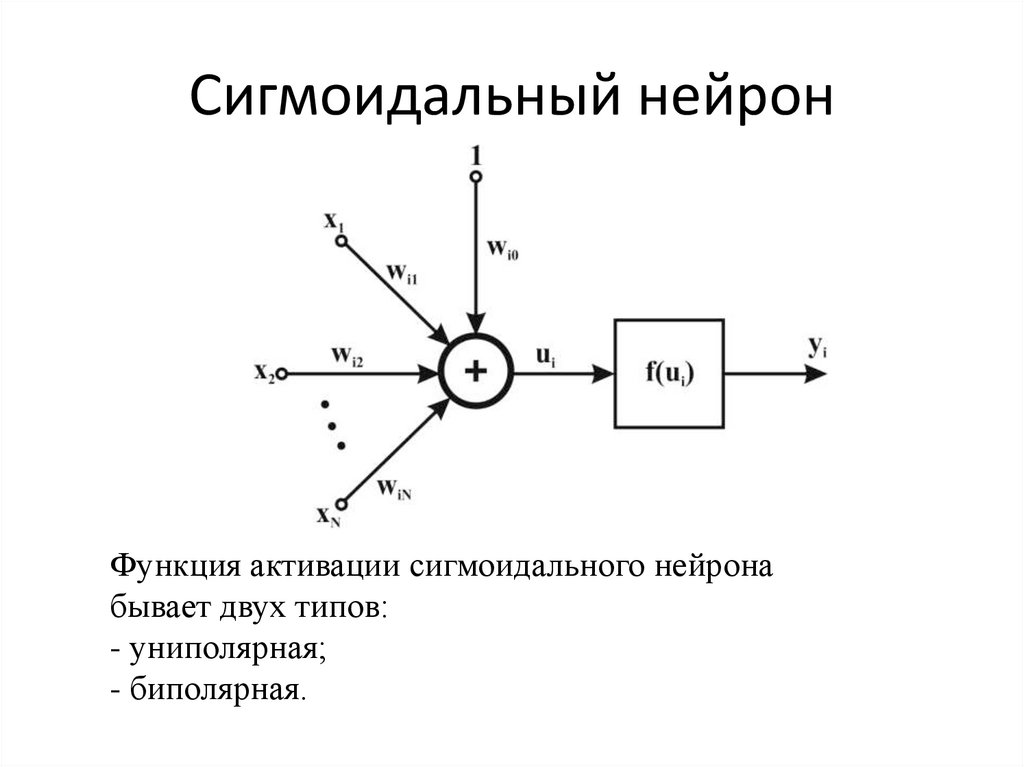
9. Сигмоидальный нейрон
Функция активации сигмоидального нейронабывает двух типов:
- униполярная;
- биполярная.
10.
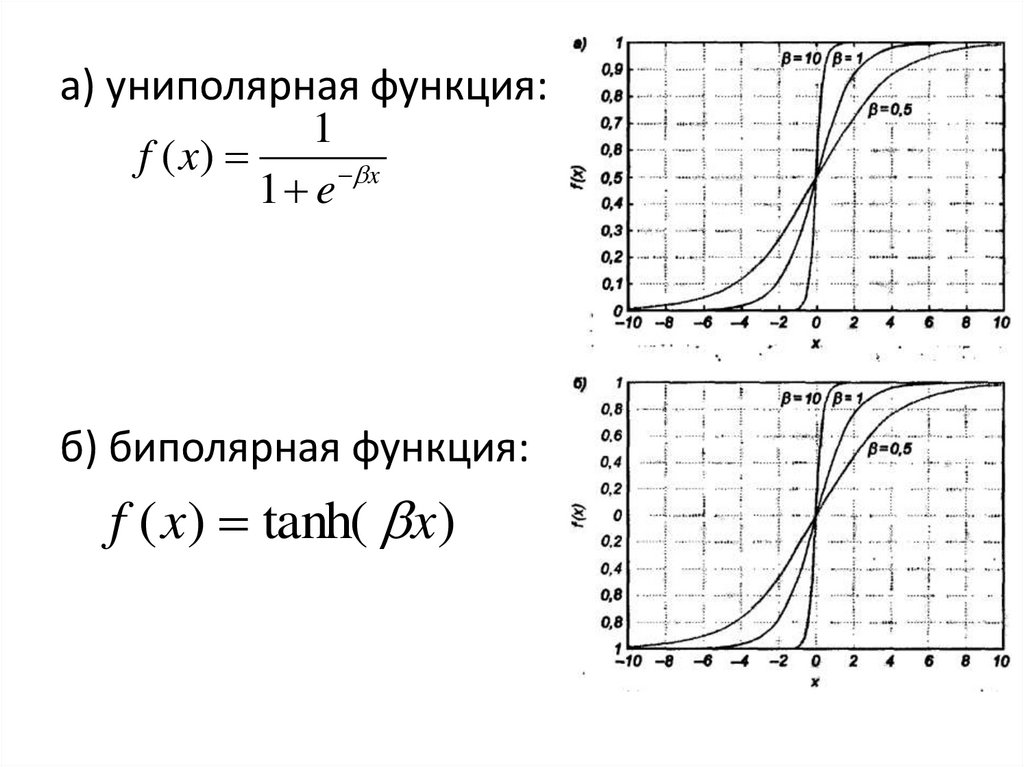
а) униполярная функция:1
f ( x)
1 e x
б) биполярная функция:
f ( x) tanh( x)
11.
а) Дифференциал униполярной функции:df ( x)
f ( x)(1 f ( x))
dx
б) Дифференциал биполярной функции:
df ( x)
2
(1 f ( x))
dx
12.
Сигмоидальный нейрон обучается с учителемпутем минимизации целевой функции:
1
2
E ( yi d i )
2
где
N
yi f (ui ) f ( wij x j )
j 0
Градиент целевой функции имеет следующий
вид:
df (ui )
dE
jE
ei x j
dwij
dui
где ei yi di
13.
Если ввести обозначение:df (ui )
i ei
dui
то градиент целевой функции примет
следующий вид:
j E x j i
а
уточнение
весовых
коэффициентов
производиться по следующей формуле:
wi j (t 1) wi j (i) i x j ;
Где - коэффициент обучения, в диапазоне
от 0 до 1.
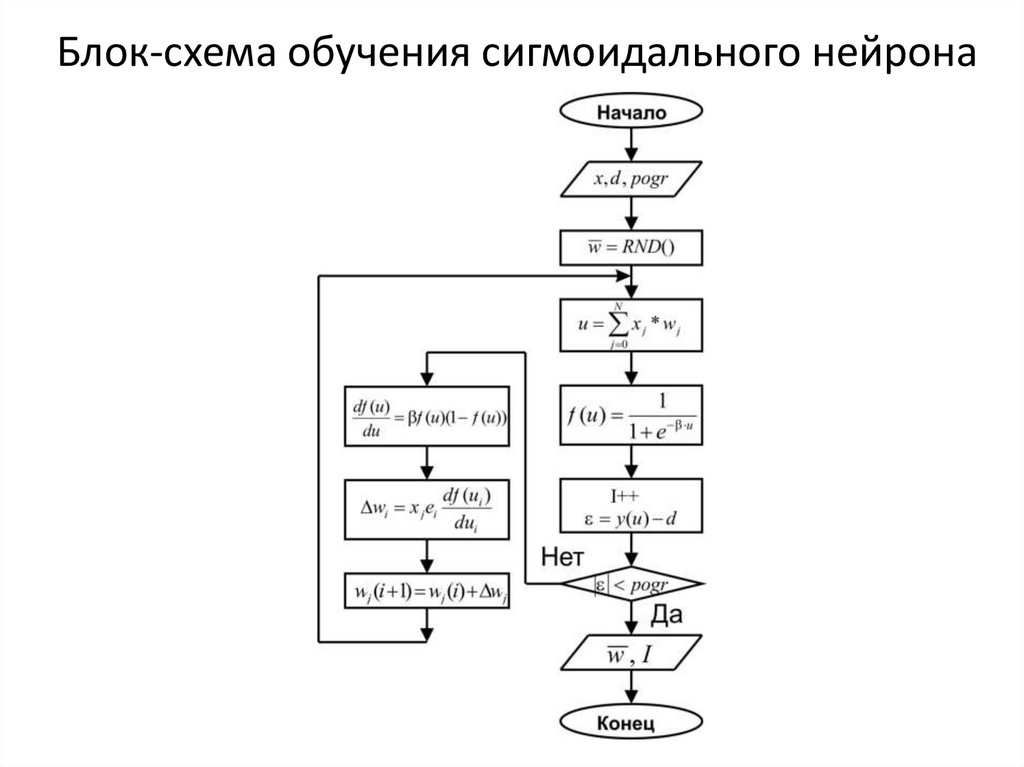
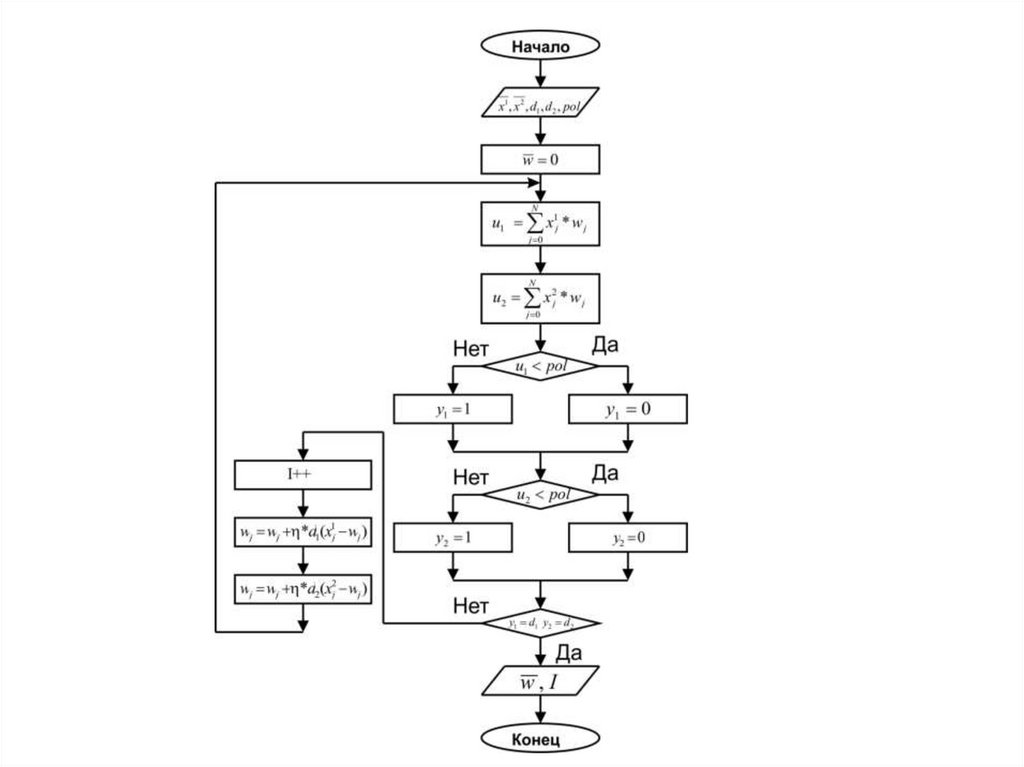
14. Блок-схема обучения сигмоидального нейрона
15.
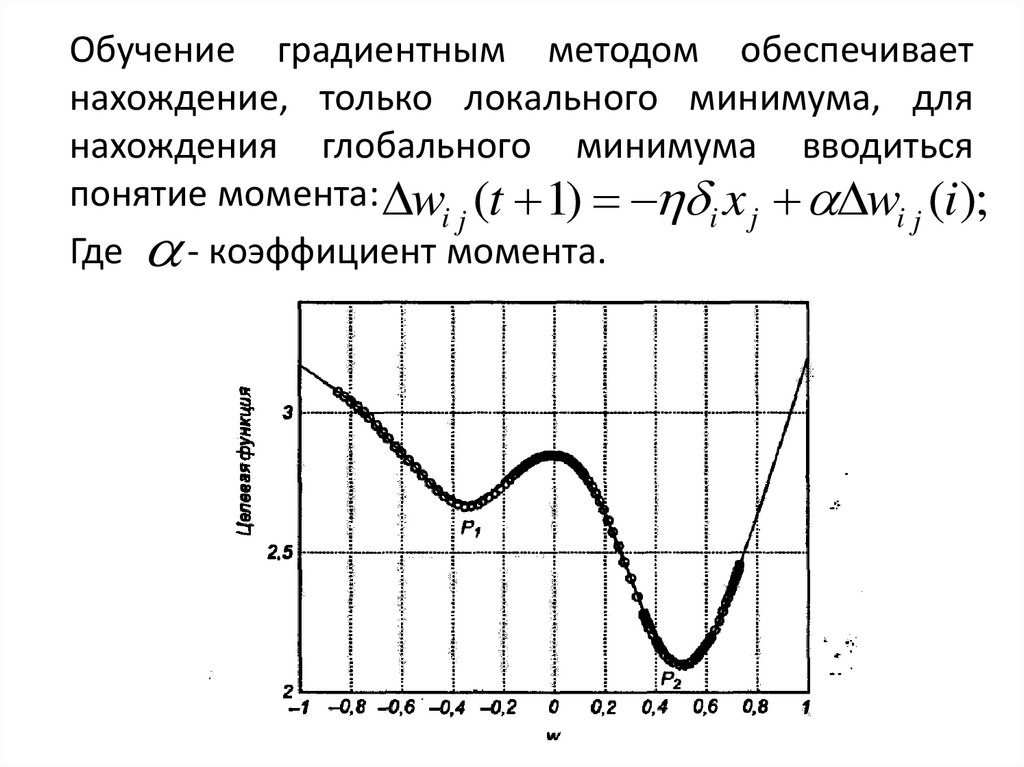
Обучение градиентным методом обеспечиваетнахождение, только локального минимума, для
нахождения глобального минимума вводиться
понятие момента: w (t 1) x w (i);
ij
i j
ij
Где - коэффициент момента.
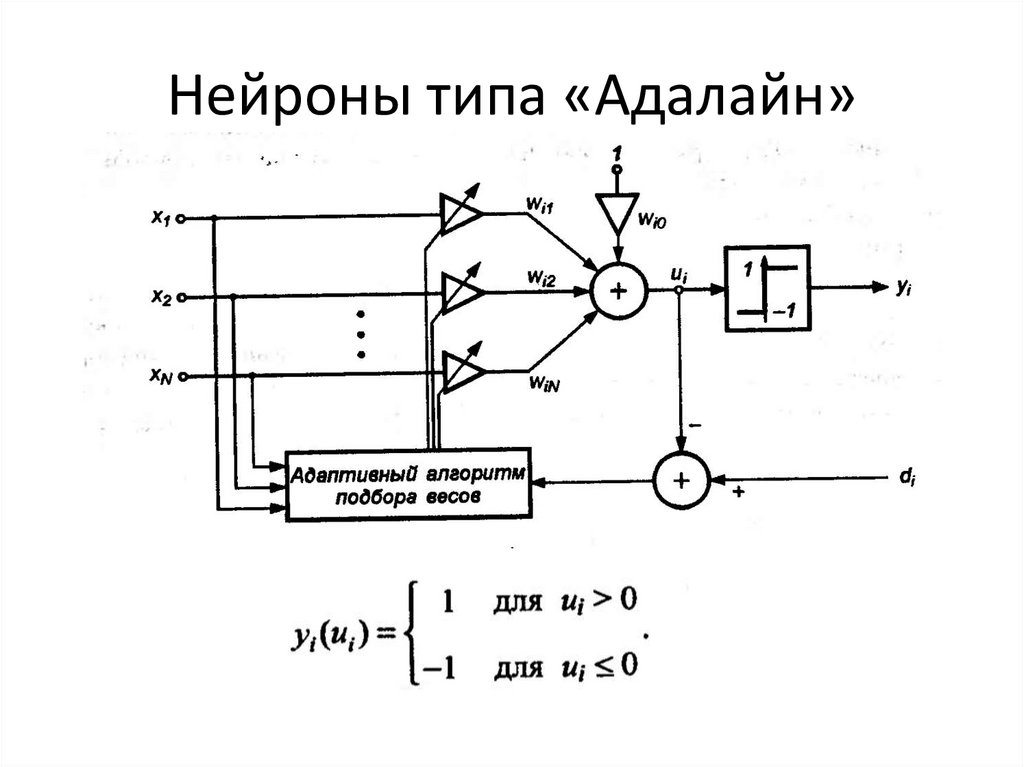
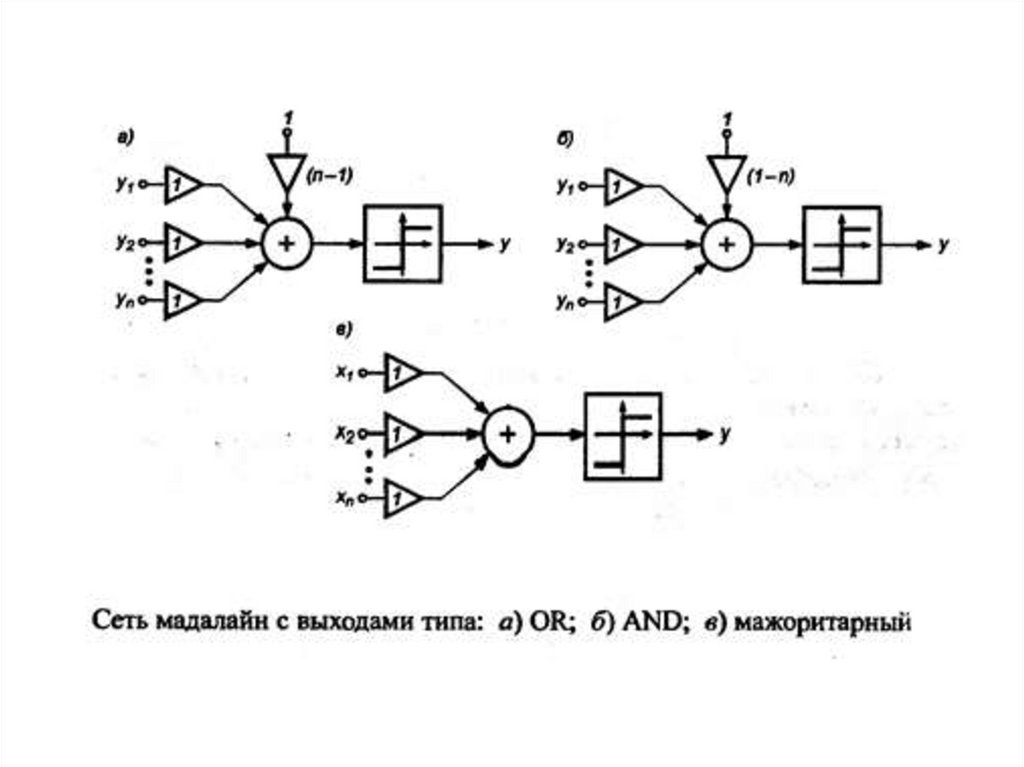
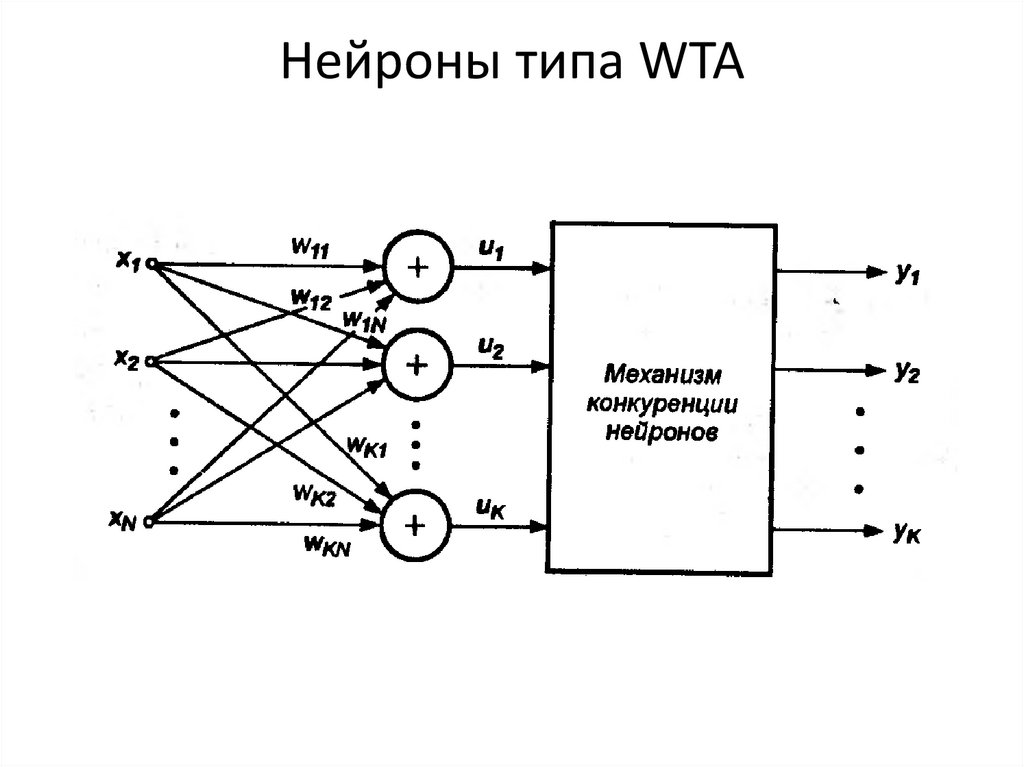
16. Нейроны типа «Адалайн»
17.
18.
19.
20.
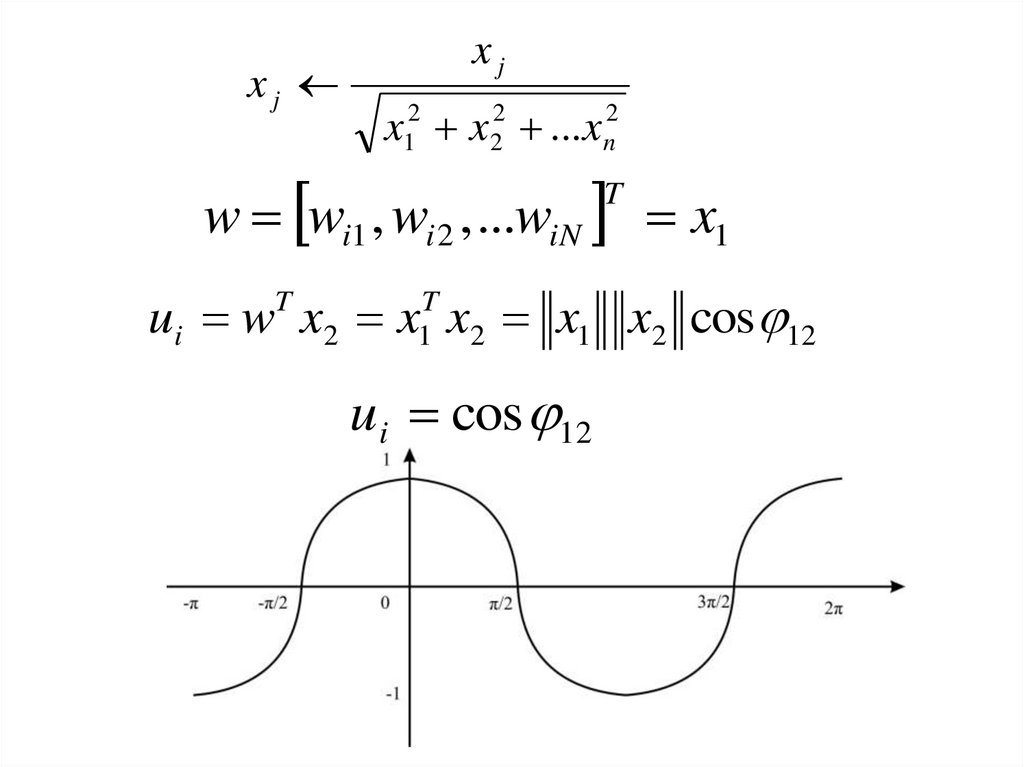
xjxj
x12 x 22 ...x n2
w wi1 , wi 2 , ...wiN x1
T
ui w x2 x x2 x1 x2 cos 12
T
T
1
ui cos 12
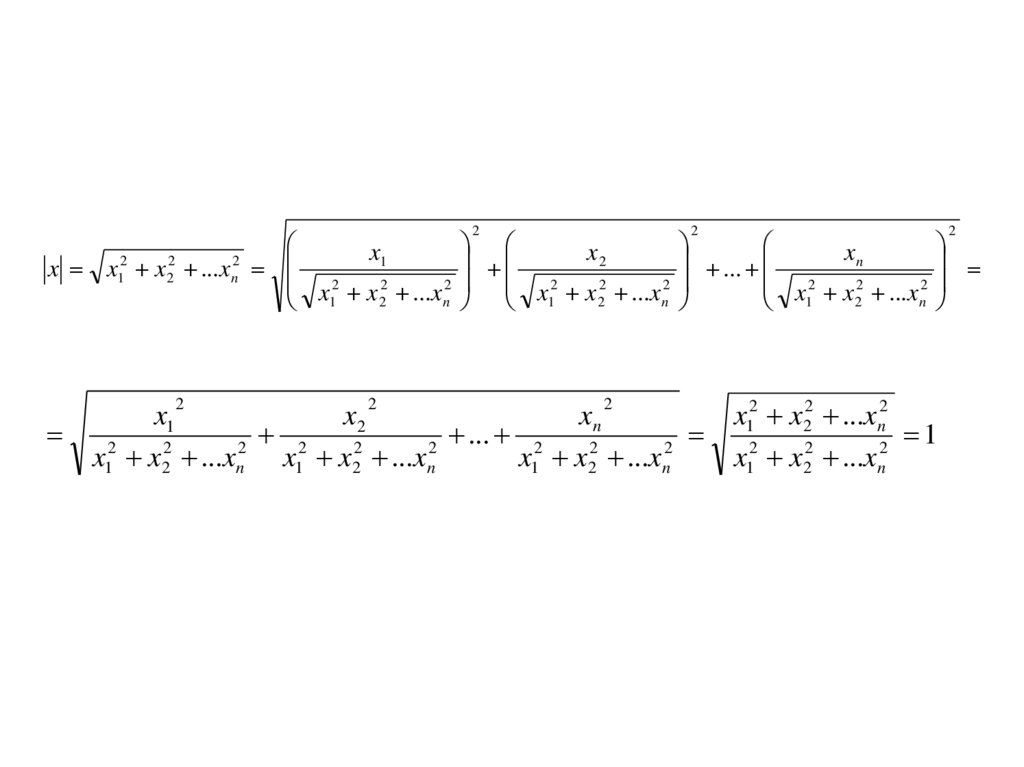
21.
x12
2
2
x x1 x 2 ...x n
x 2 x 2 ...x 2
2
n
1
2
2
2
x2
x 2 x 2 ...x 2
2
n
1
2
2
xn
...
x 2 x 2 ...x 2
2
n
1
xn
x1
x2
...
2
2
2
2
2
2
2
2
2
x1 x2 ...xn x1 x2 ...xn
x1 x2 ...xn
2
x12 x22 ...xn2
1
2
2
2
x1 x2 ...xn







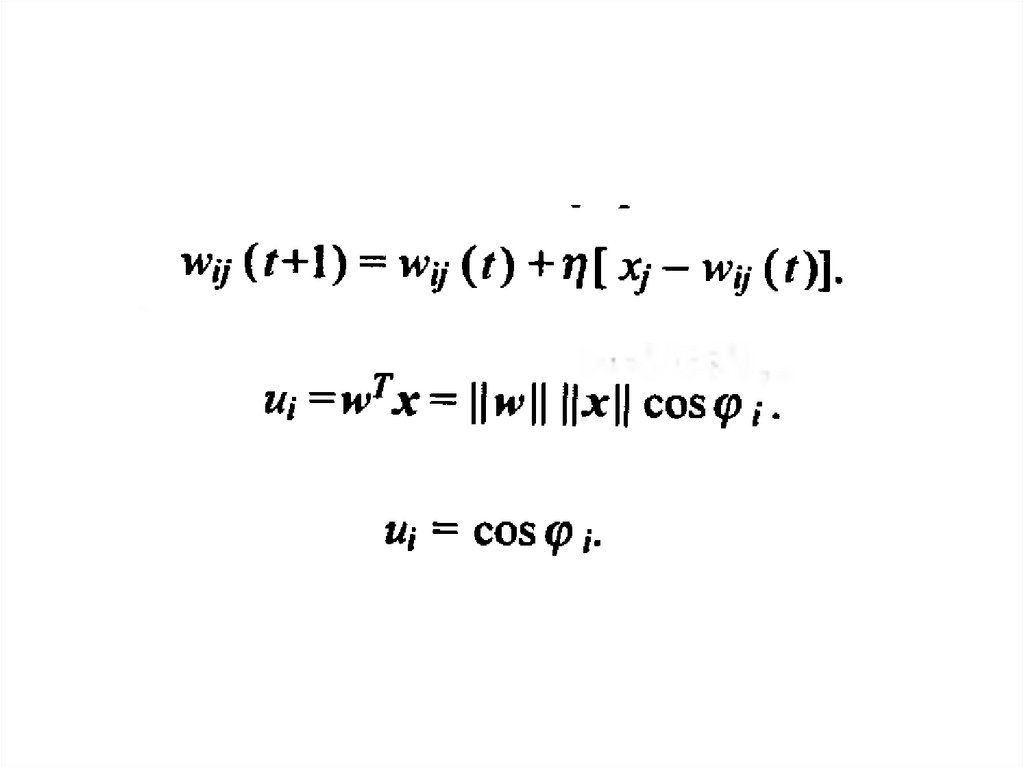





 informatics
informatics








