Similar presentations:
Обратные тригонометрические функции
1.
Обратныетригонометрические функции
2.
Арксинусом числа a (обозначается arcsina)называется значение угла x в интервале [−π/2,π/2],
при котором sinx=a.
Обратная функция y=arcsinx определена при x∈[−1,1],
область ее значений равна y∈[−π/2,π/2].
3.
Арккосинусом числа a (обозначается arccosa)называется значение угла x в интервале [0,π],
при котором cosx=a.
Обратная функция y=arccosx
определена при x∈[−1,1],
область ее значений принадлежит
отрезку y∈[0,π].
4.
Арктангенсом числа a (обозначается arctga)называется значение угла x в открытом интервале (−π/2,π/2),
при котором tgx=a.
Обратная функция y=arctgx определена при всех x∈R,
область значений арктангенса равна y∈(−π/2,π/2).
5.
Арккотангенсом числа a (обозначается arcctg a)называется значение угла x в открытом интервале [0,π],
при котором ctgx=a.
Обратная функция y=arcctg x определена при всех x∈R,
область ее значений находится в интервале y∈[0,π].
6.
Что означает выражение arcsin 0,4 ?Это угол, синус которого равен 0,4 !
и еще
arcsin(sina)=a
arccos(cosa) =a
arctg(tga)=a
arcctg(ctga)=a
7.
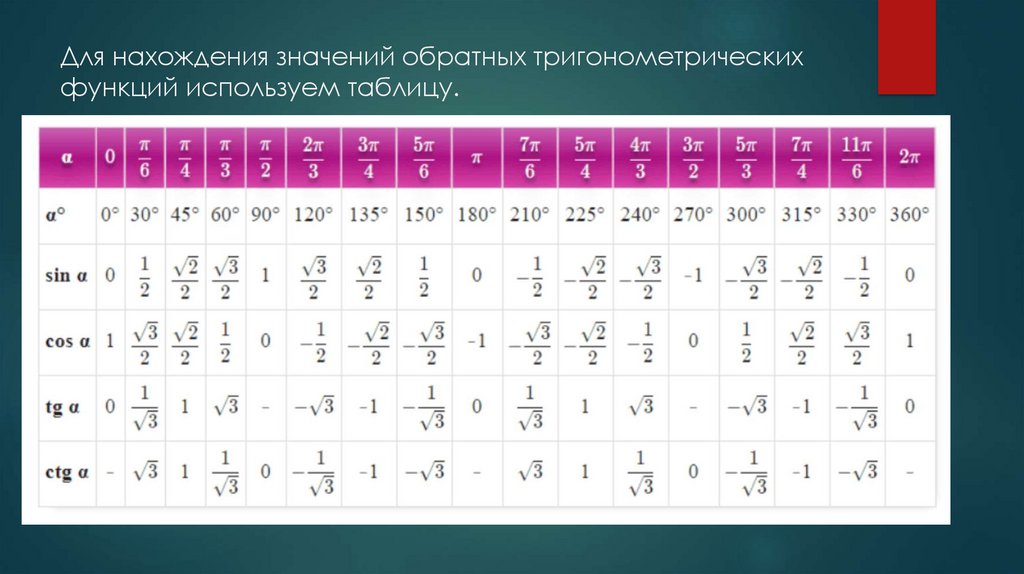
Для нахождения значений обратных тригонометрическихфункций используем таблицу.
8.
Примеры нахождения значений обратныхтригонометрических функций
Найдите значения:
arcsin 0,5 = 30° или arcsin 1/2 =π/6
1. sin(arcsin 0,5) =
arctg1 = π/4
2. sin(arcsin 0,4) =
arccos ½= π/3
3. cos(arcsin 0,6) =
arcctg √3 = π/6
4. tg(arcsin 12/13) =
arctg√3 = π/3
5. arcsin(sin π/6) =
Arccos (√3/2)= π/6
6. arctg(tg π/5) =
7. arccos(cos 4π/3) =
8. arccos(cos9π/8) =
9.
Свойства обратныхтригонометрических функций
10.
Решить примеры:arcсos (- l) + arcctg 0 + 3 arcsin 0,5
arcctg (-1) - 2 arccos + arctg 1
2.1 arcsin (-1) + 2 arcctg 1 – arcsin 0
5 arcsin 0 +2 arctg 1 + arсcos0,5
0,5 arccos(-1 ) - arctg 0 - arcctg 1
11.
Решение тригономическихуравнений










 mathematics
mathematics








