Similar presentations:
Обратные тригонометрические функции
1. Обратные тригонометрические функции.
2.
На отрезкеy=sin(x) монотонно возрастает,
поэтому на нём можно определить обратную ему
функцию. Она называется арксинус y=arcsin (x).
Определение:
Если число x [-1;1], то arcsin (x) - это угол,
синус которого равен x.
3.
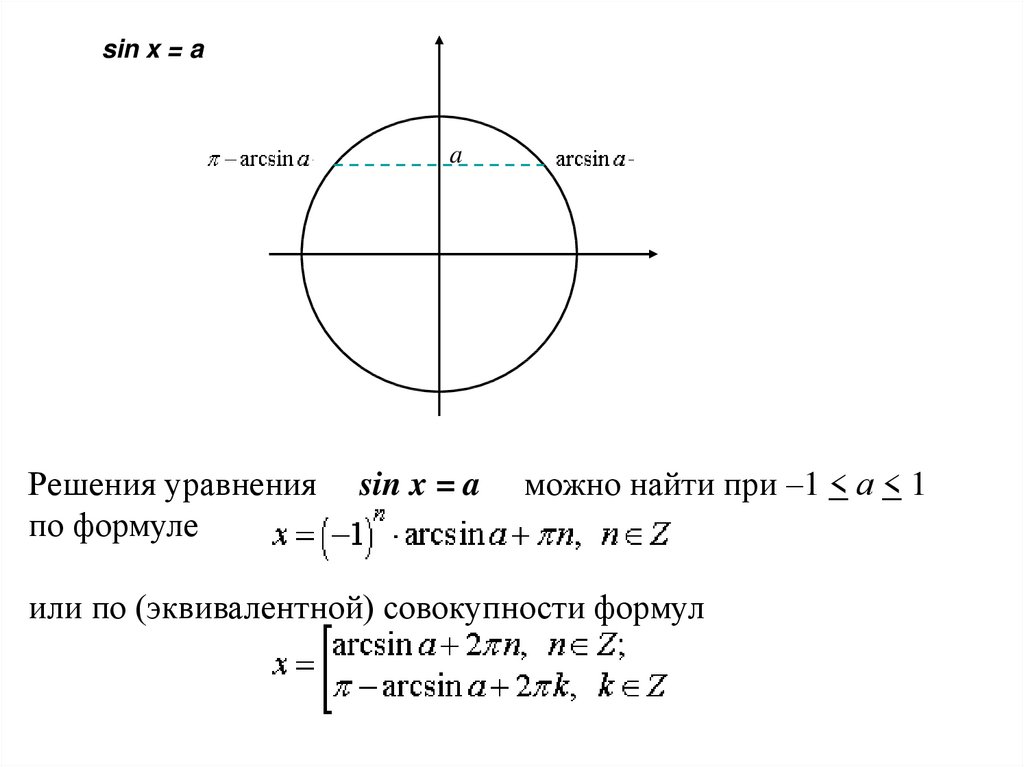
sin x = aa
Решения уравнения
по формуле
sin x = a
можно найти при –1 < а < 1
или по (эквивалентной) совокупности формул
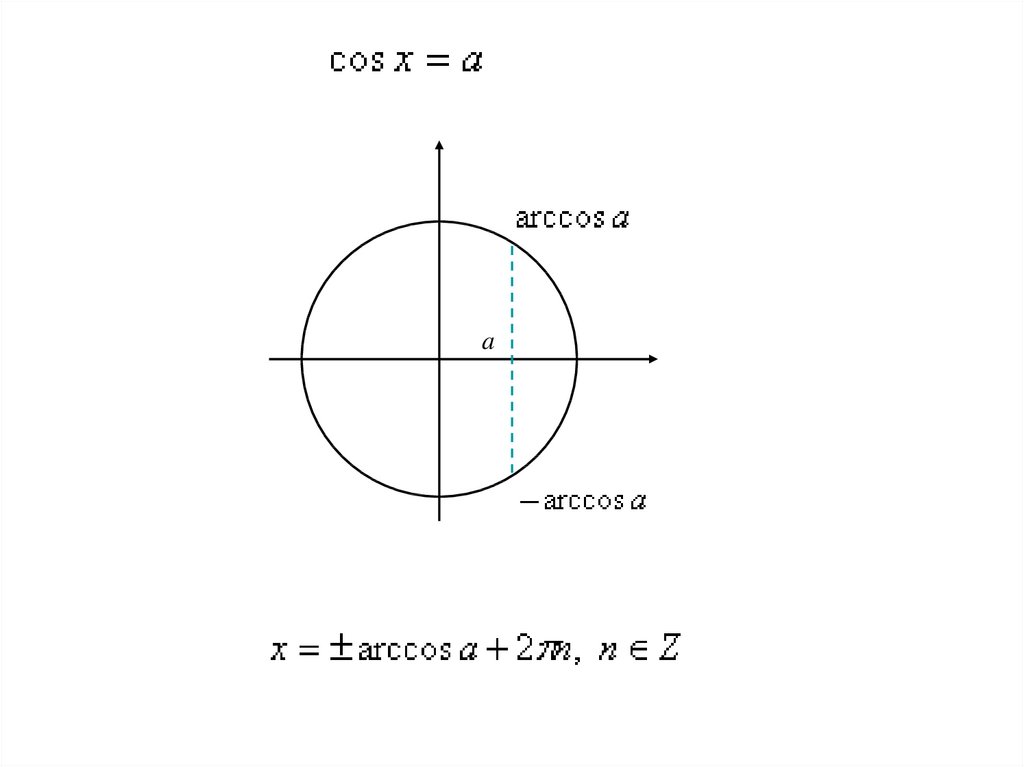
4. На отрезке [0; π] косинус монотонно убывает, поэтому на этом промежутке можно определить обратную ему функцию. Она называется
арккосинусОпределение:
arccos (x) это угол, косинус которого равен x.
Если x = cos( ), то arccos (x) = .
5.
a6.
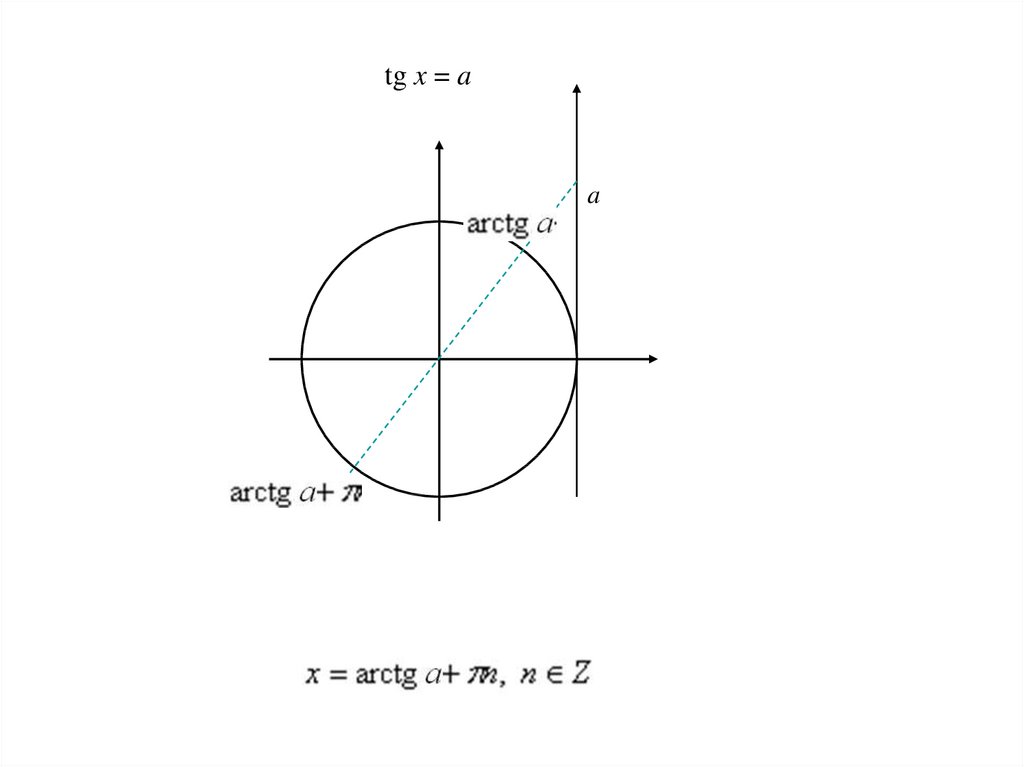
На интервалетангенс возрастает, поэтому на этом
множестве можно определить обратную ему функцию. Она
называется арктангенс:
Определение:
arctg (x) это угол, тангенс которого равен x.
Если x = tg( ), то arctg(x) = .
7.
tg x = aa
8.
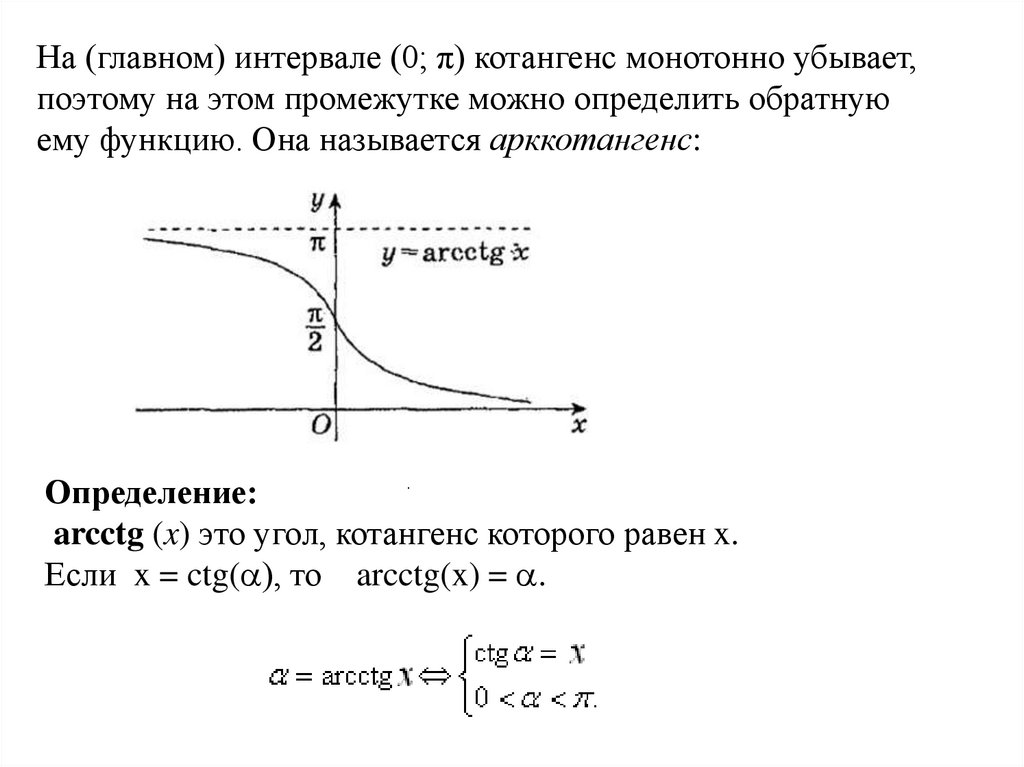
На (главном) интервале (0; π) котангенс монотонно убывает,поэтому на этом промежутке можно определить обратную
ему функцию. Она называется арккотангенс:
.
Определение:
arcctg (x) это угол, котангенс которого равен x.
Если x = ctg( ), то arcctg(x) = .
9.
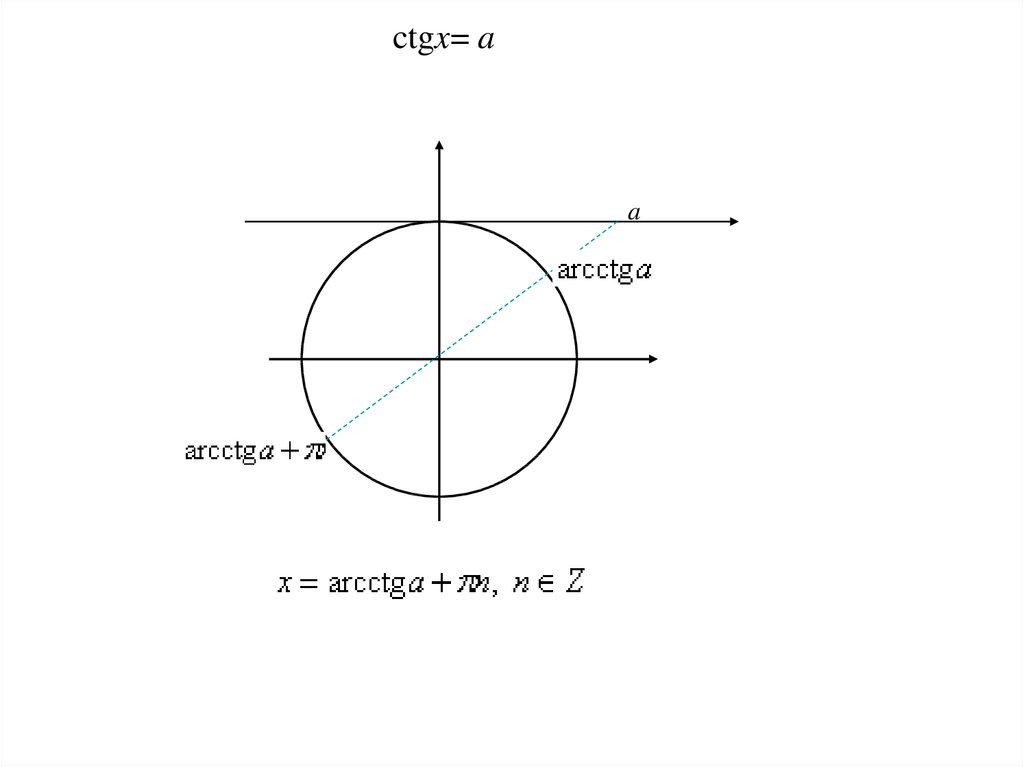
ctgx= aa


![На отрезке [0; π] косинус монотонно убывает, поэтому на этом промежутке можно определить обратную ему функцию. Она называется На отрезке [0; π] косинус монотонно убывает, поэтому на этом промежутке можно определить обратную ему функцию. Она называется](https://cf2.ppt-online.org/files2/slide/d/DXEtwOpQfkr4HyR8m92S3KFzjCbBAdV0gaoh6c/slide-3.jpg)













 mathematics
mathematics








