Similar presentations:
Обратные тригонометрические функции и их свойства
1.
Обратные тригонометрическиефункции и их свойства
2.
,При каких значениях t верно равенство?
sint = 0,5
sint = 0,3
t=?
3.
Обратныетригонометрические функции
у=arcsinx
у=arcctgx
график
график
у=arccosx
график
у=arctgx
график
4.
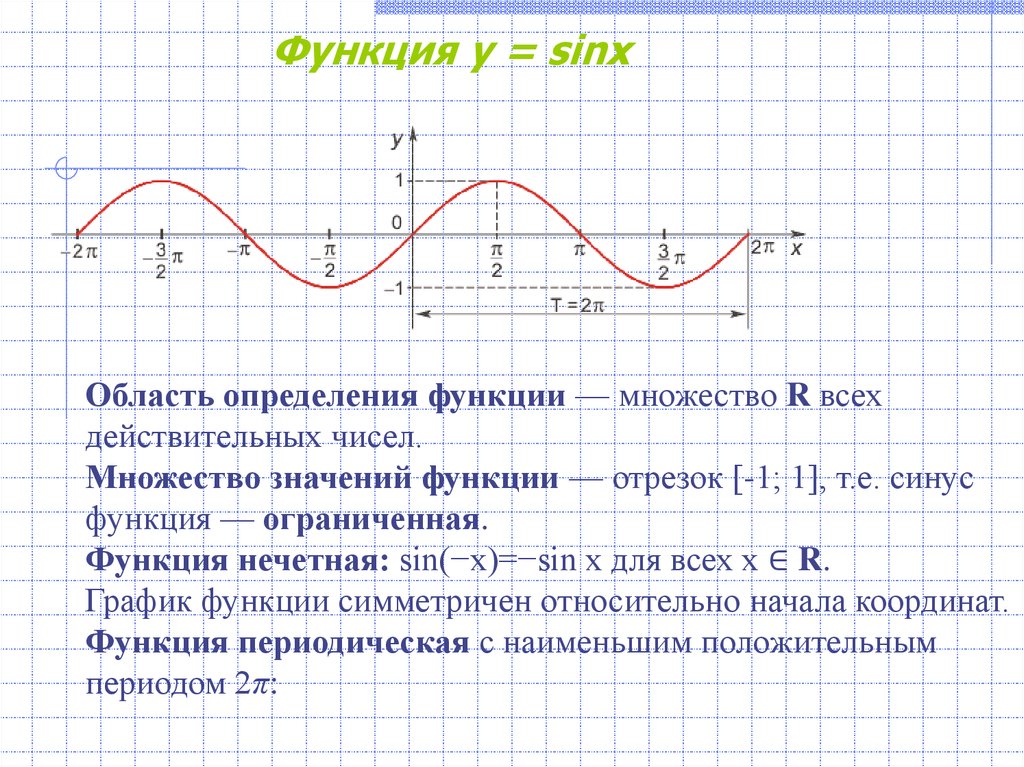
Функция у = sinxОбласть определения функции — множество R всех
действительных чисел.
Множество значений функции — отрезок [-1; 1], т.е. синус
функция — ограниченная.
Функция нечетная: sin(−x)=−sin x для всех х ∈ R.
График функции симметричен относительно начала координат.
Функция периодическая с наименьшим положительным
периодом 2π:
5.
Функция y=arcsinx и ее свойстваЕсли |а| ≤ 1, то arcsin а – это такое число
из отрезка [-π/2; π/2], синус которого
равен а.
Если |а| ≤ 1, то
arcsin а = t
sin t = а,
-π/2 ≤ t ≤ π/2;
sin (arcsin a) = a
6.
Функция y=arcsinx и ее свойства1. D(y) = [-1; 1].
2. E(y) = [-π/2; π/2].
3. arcsin (-x) = - arcsin x – функция
нечетная.
4. Функция возрастает на [-1; 1].
5. Функция непрерывна.
7.
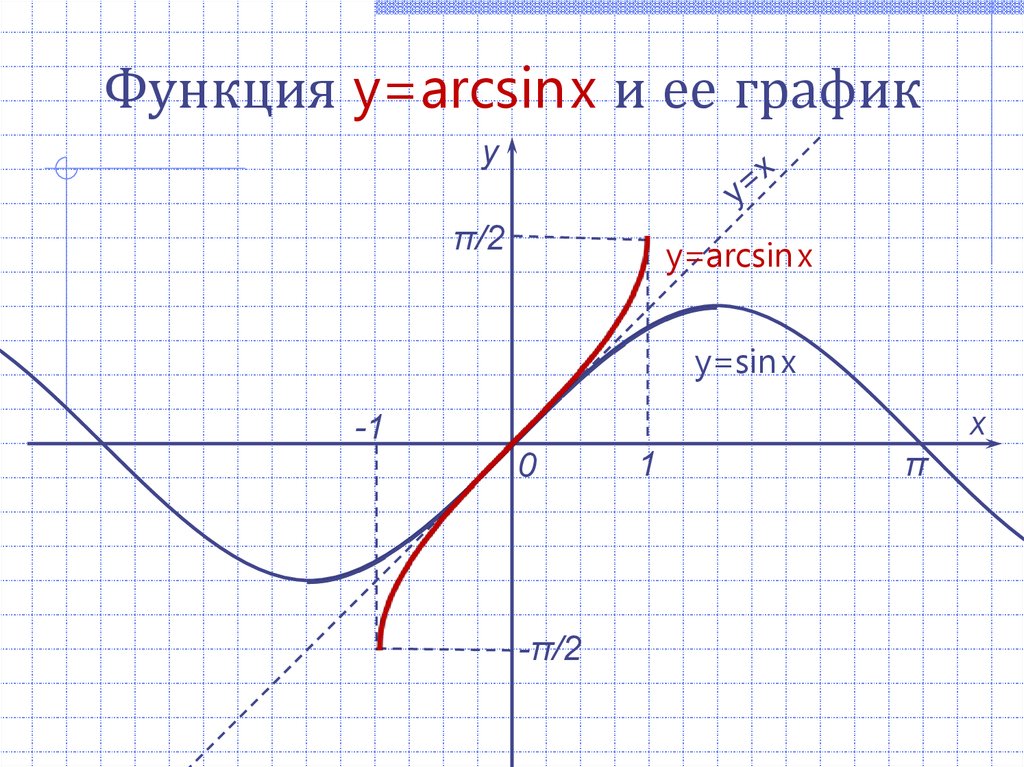
Функция y=arcsinx и ее графику
π/2
y=arcsin x
y=sin x
х
-1
0
-π/2
1
π
8.
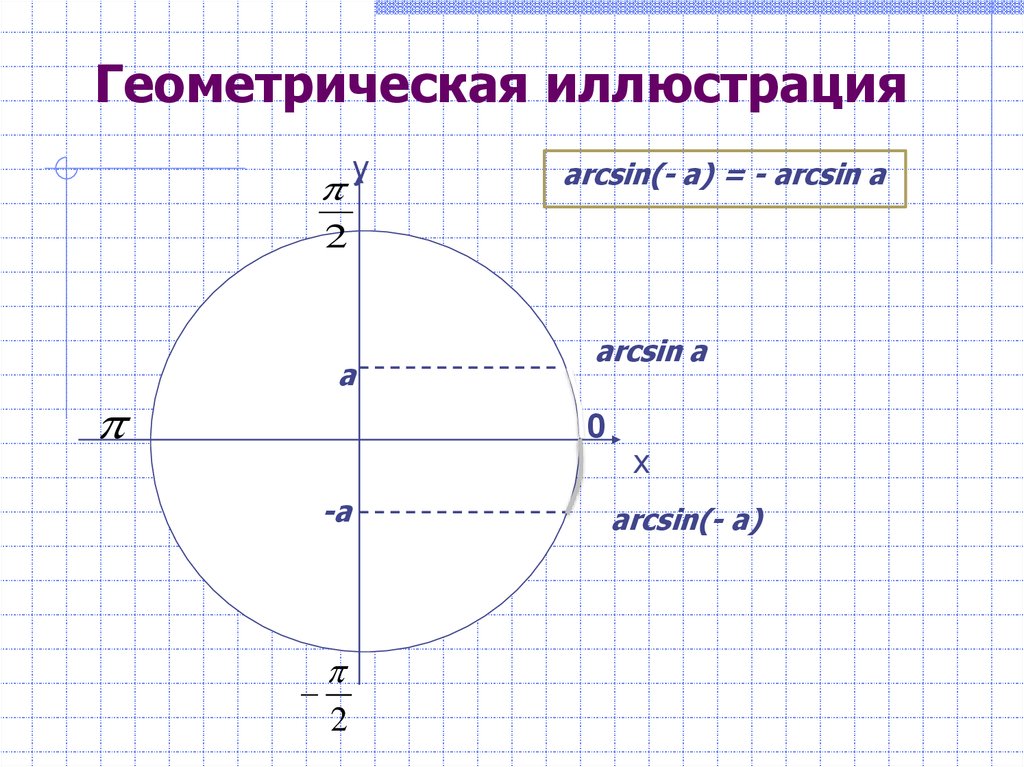
Геометрическая иллюстрацияу
arcsin(- a) = - arcsin a
2
a
arcsin a
0
-a
2
х
arcsin(- a)
9.
Функция у = cosxОбласть определения функции — множество R всех
действительных чисел.
Множество значений функции — отрезок [-1; 1], т.е.
косинус функция — ограниченная.
Функция четная: cos(−x)=cos x для всех х ∈ R.
График функции симметричен относительно оси OY.
Функция периодическая с наименьшим положительным
периодом 2π:
10.
Функция y=arccosx и ее свойстваЕсли |а| ≤ 1, то arccos а – это такое число
из отрезка [0; π], косинус которого равен
а.
Если |а| ≤ 1, то
arccos а = t
cos t = а,
0 ≤ t ≤ π;
cos (arccos a) = a
arccos (-a) = π – arccos a, где -1 ≤ а ≤ 1
11.
Функция y=arccosx и ее свойства1. D(y) = [-1; 1].
2. E(y) = [0; π].
3. Функция не является ни четной, ни
нечетной.
4. Функция убывает на [-1; 1].
5. Функция непрерывна.
12.
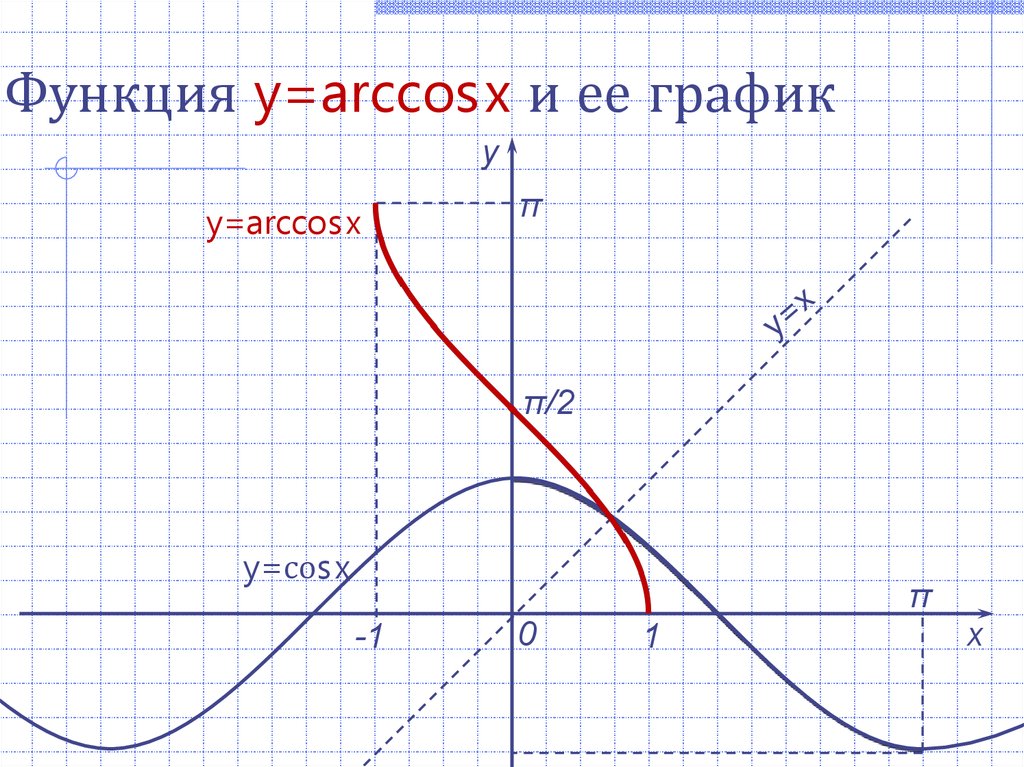
Функция y=arccosx и ее графику
y=arccos x
π
π/2
y=соs x
π
-1
0
1
х
13.
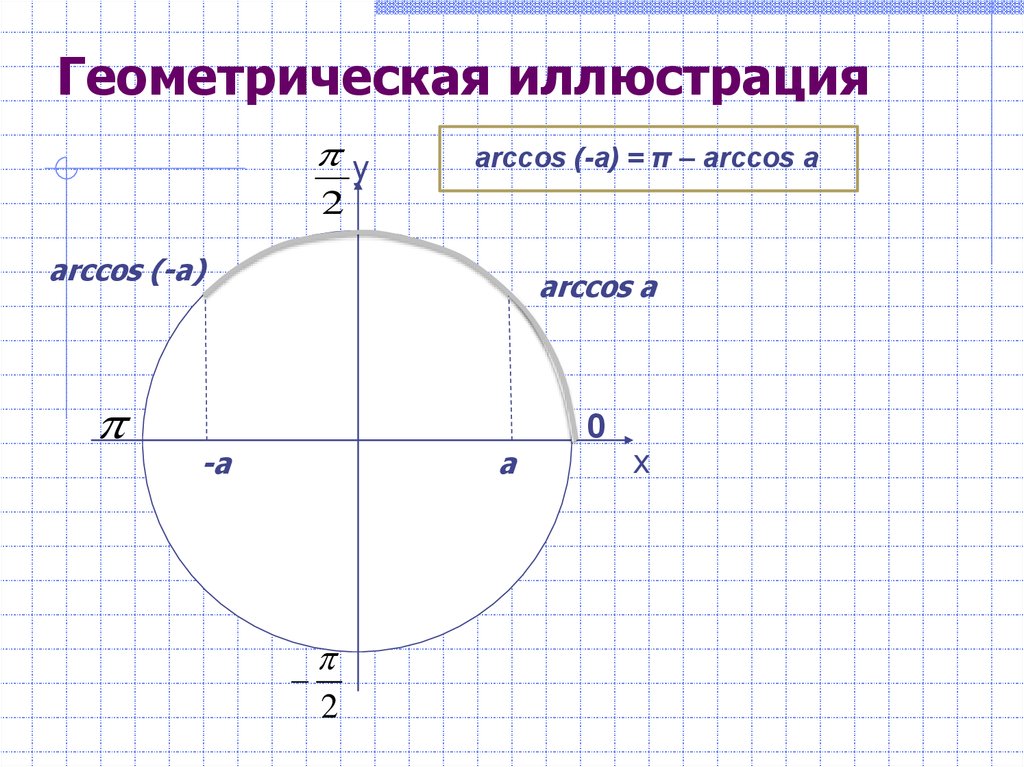
Геометрическая иллюстрацияу
arccos (-a) = π – arccos a
2
arccos (-a)
arccos a
-a
a
2
0
х
14.
Функция y=arctgx и ее свойстваarctg а – это такое число из интервала (-π/2;
π/2), тангенс которого равен а.
arctg а = t
tg t = а,
-π/2 < t < π/2;
tg (arctg a) = a
15.
Функция y=arctgx и ее свойства1. D(y) = (- ; + ).
2. E(y) = (-π/2; π/2).
3. arctg (-x) = - arctg x – функция нечетная.
4. Функция возрастает на (- ; + ).
5. Функция непрерывна.
16.
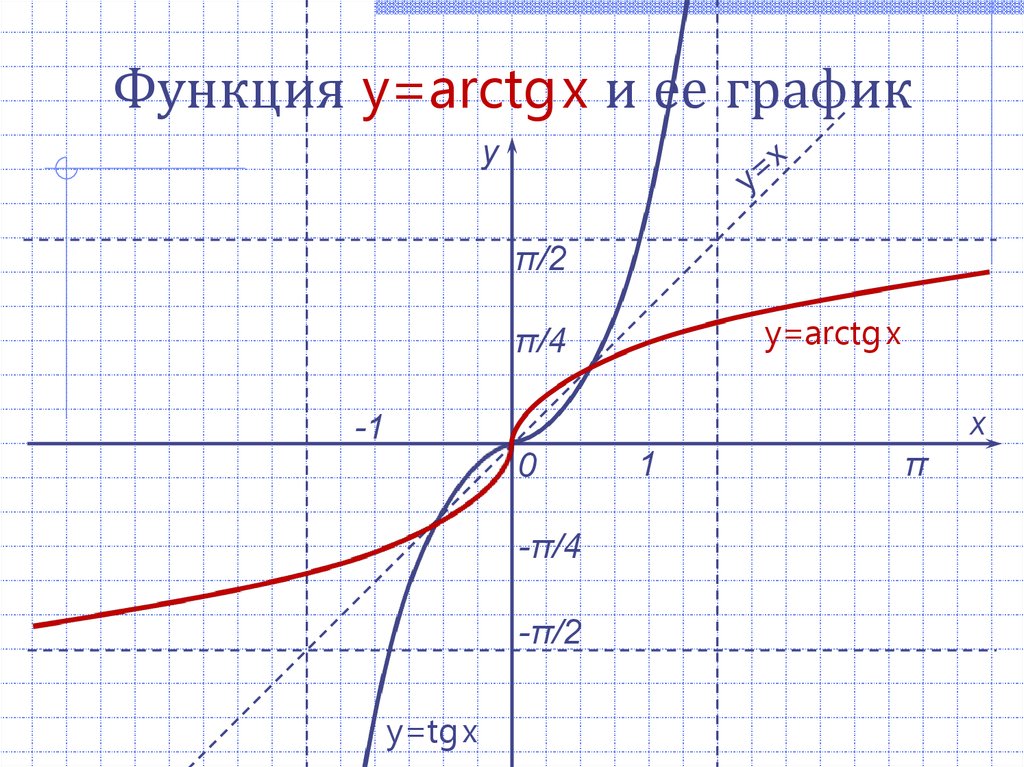
Функция y=arctgx и ее графику
π/2
y=arctg x
π/4
х
-1
0
-π/4
-π/2
y=tg x
1
π
17.
Функция y=arcсtgx и ее свойстваarcсtg а – это такое число из интервала (0;
π), котангенс которого равен а.
arcсtg а = t
сtg t = а,
0 < t < π;
сtg (arcсtg a) = a
arcctg (-a) = π – arcctg a
18.
Функция y=arcсtgx и ее свойства1. D(y) = (- ; + ).
2. E(y) = (0; π).
3. Функция не является ни четной, ни
нечетной.
4. Функция убывает на (- ; + ).
5. Функция непрерывна.
19.
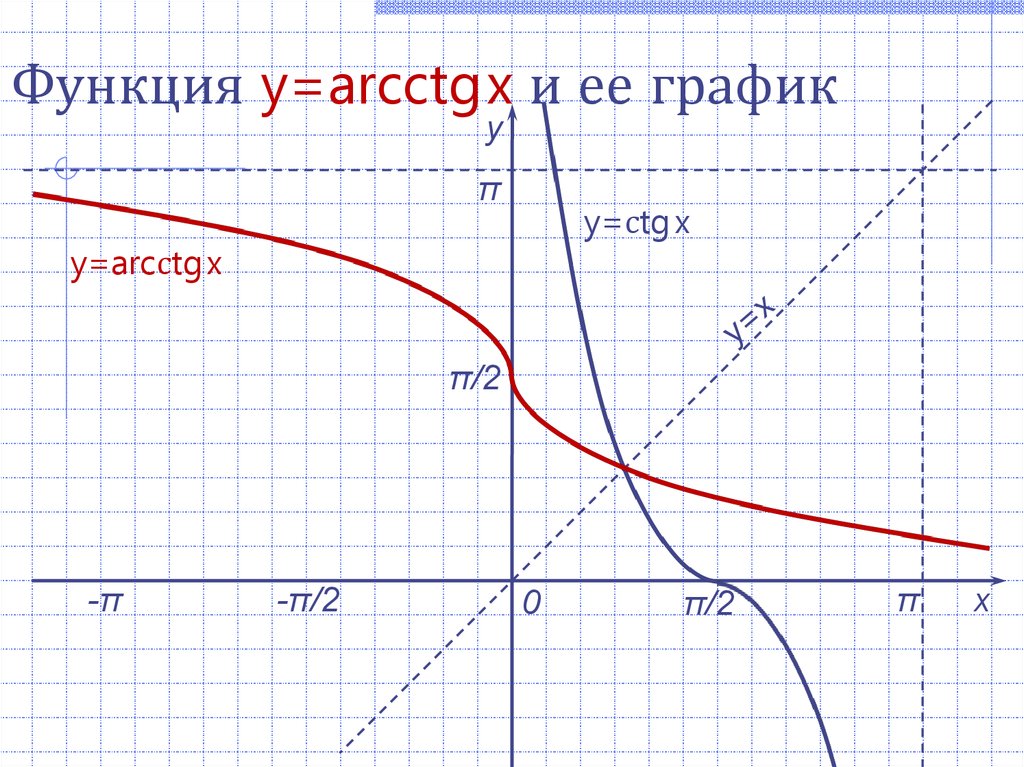
Функция y=arcctgx и ее графику
π
y=сtg x
y=arcсtg x
π/2
-π
-π/2
0
π/2
π
х
20.
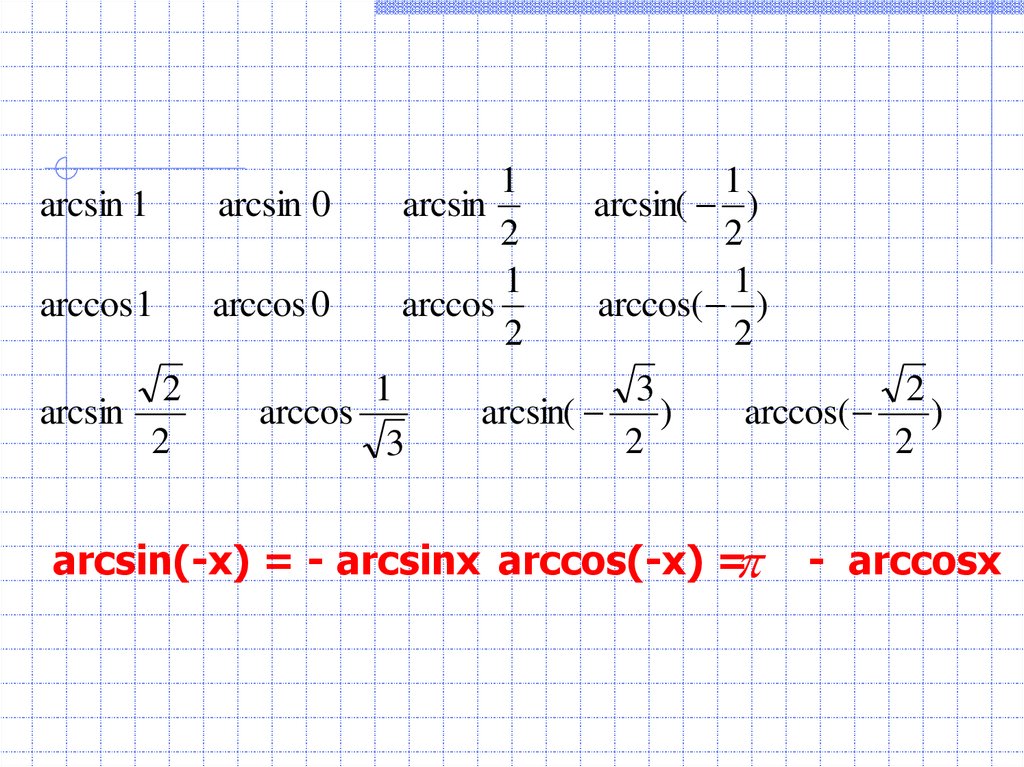
arcsin 1arcsin 0
arccos 1
arccos 0
2
arcsin
2
1
arcsin
2
1
arccos
2
1
arccos
3
1
arcsin( )
2
1
arccos( )
2
3
2
arcsin( )
arccos(
)
2
2
arcsin(-x) = - arcsinx arccos(-x) =
- arccosx
21.
Имеет ли смысл выражение?arcsin 2 arccos 3
arctg100
Может ли arcsint и arccost принимать
значение равное
5
5, , , 10,
9
3
,?
7
22.
Найдите значения выражений:arccos(cos )
3
5
arcsin(sin
)
2
7
ctg (arcctg ( ))
8
tg (arctg15)
5
sin(arcsin
)
13
3
cos(arcsin
)
2
23.
3arctg1
arctg 3
arctg (
)
3
3
arcctg1 arcctg 3
arcctg (
)
3
arctg(-x) = - arctgx
arcctg(-x) = - arcctgx
24.
Свойства аркфункцийcos(arccos x) x,
arccos(cos x) x, x 1;1
sin(arcsin x) x,
arcsin(sin x) x, x 1;1
tg (arctgx) x
arctg (tgx) x,
ctg (arcctgx) x
arcctg (ctgx) x.
25.
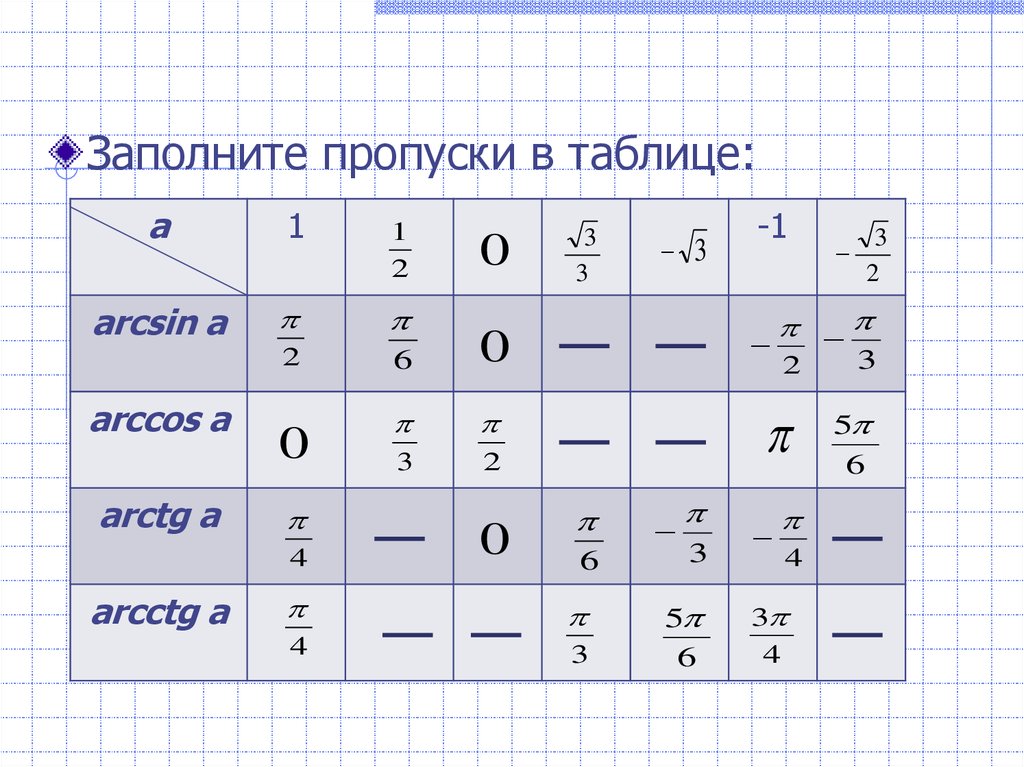
Заполните пропуски в таблице:a
arcsin a
arccos a
arctg a
1
0
2
6
0
3
2
0
4
arcctg a
1
2
0
3
3
3
-1
3
2
3
2
6
4
3
3
5
6
4
3
4
5
6
26.
Вид уравненияПростейшие уравнения (по
определению аркфункции)
Уравнения, приводимые к
квадратным уравнениям
Уравнения, левая и правая части
которых являются одноименными
тригонометрическими функциями
Уравнения, левая и правая части
которых являются разноименными
тригонометрическими функциями
Пример
















 mathematics
mathematics








