Обратные тригонометрические функции

1.

2.

«Функция, как правило, определяется
для тех значений аргумента, какие для
данной задачи представляют реальное
значение»
Хинчин А.Я.

3.

,
При каких значениях t верно равенство?
sint = 0,5
sint = 0,3
t=?

4.

Обратные
тригонометрические функции
у=arcctgx
у=arcsinx
график
график
у=arccosx
график
у=arctgx
график

5.

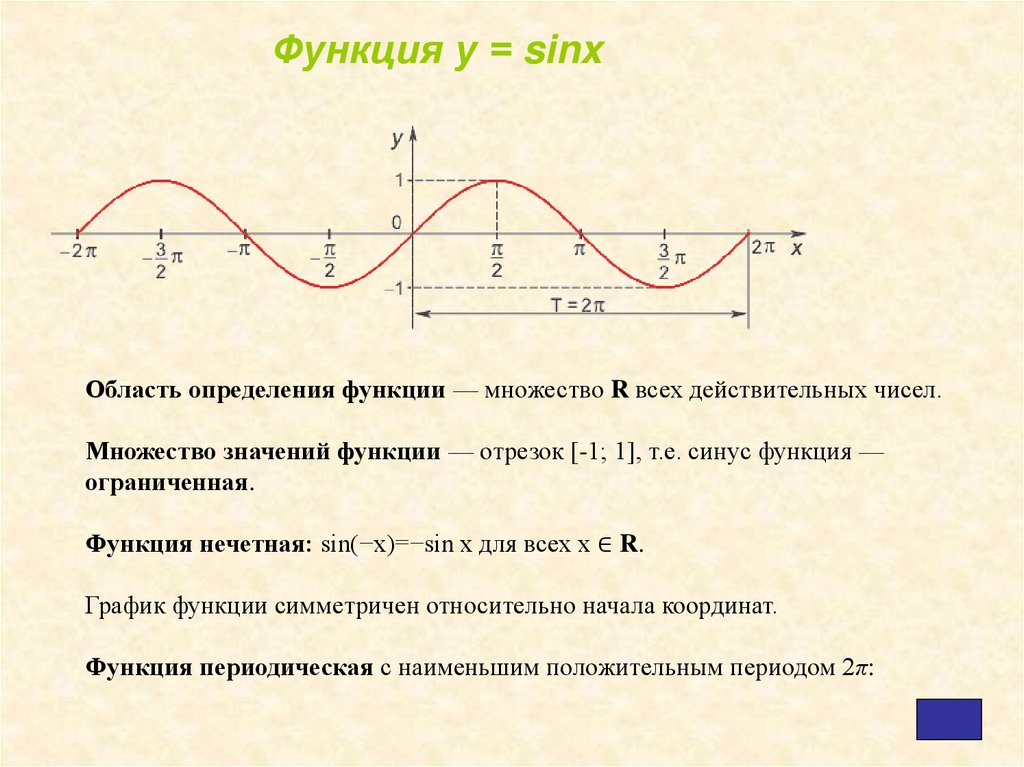
Функция у = sinx
Область определения функции — множество R всех действительных чисел.
Множество значений функции — отрезок [-1; 1], т.е. синус функция —
ограниченная.
Функция нечетная: sin(−x)=−sin x для всех х ∈ R.
График функции симметричен относительно начала координат.
Функция периодическая с наименьшим положительным периодом 2π:

6.

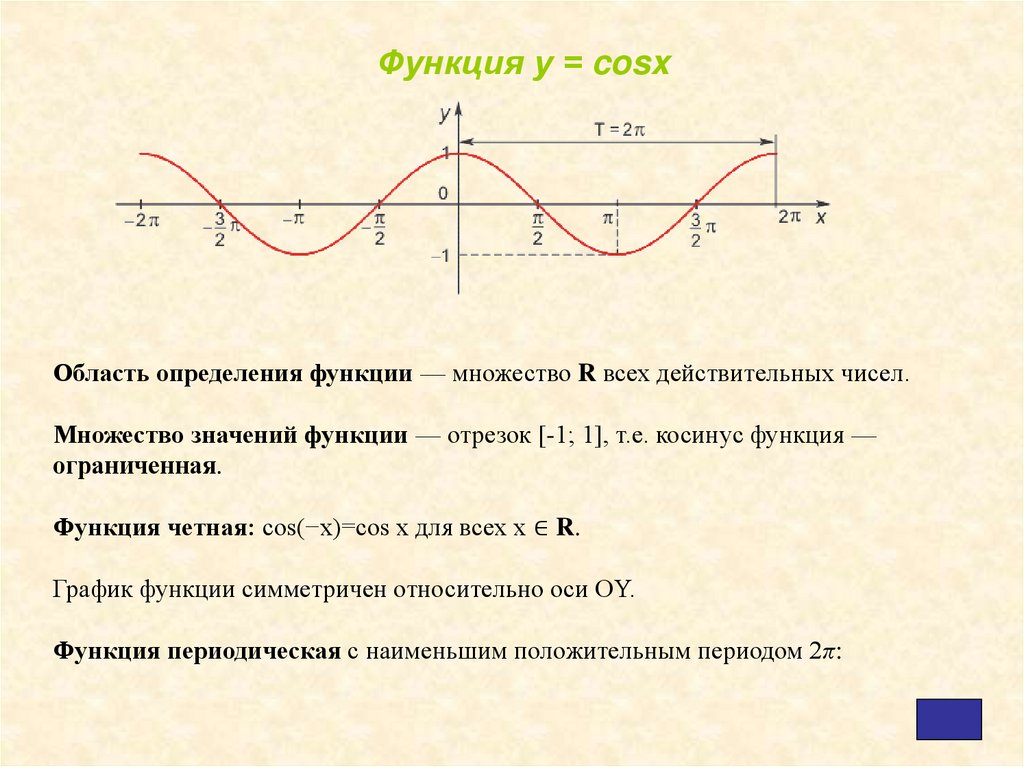
Функция у = cosx
Область определения функции — множество R всех действительных чисел.
Множество значений функции — отрезок [-1; 1], т.е. косинус функция —
ограниченная.
Функция четная: cos(−x)=cos x для всех х ∈ R.
График функции симметричен относительно оси OY.
Функция периодическая с наименьшим положительным периодом 2π:

7.

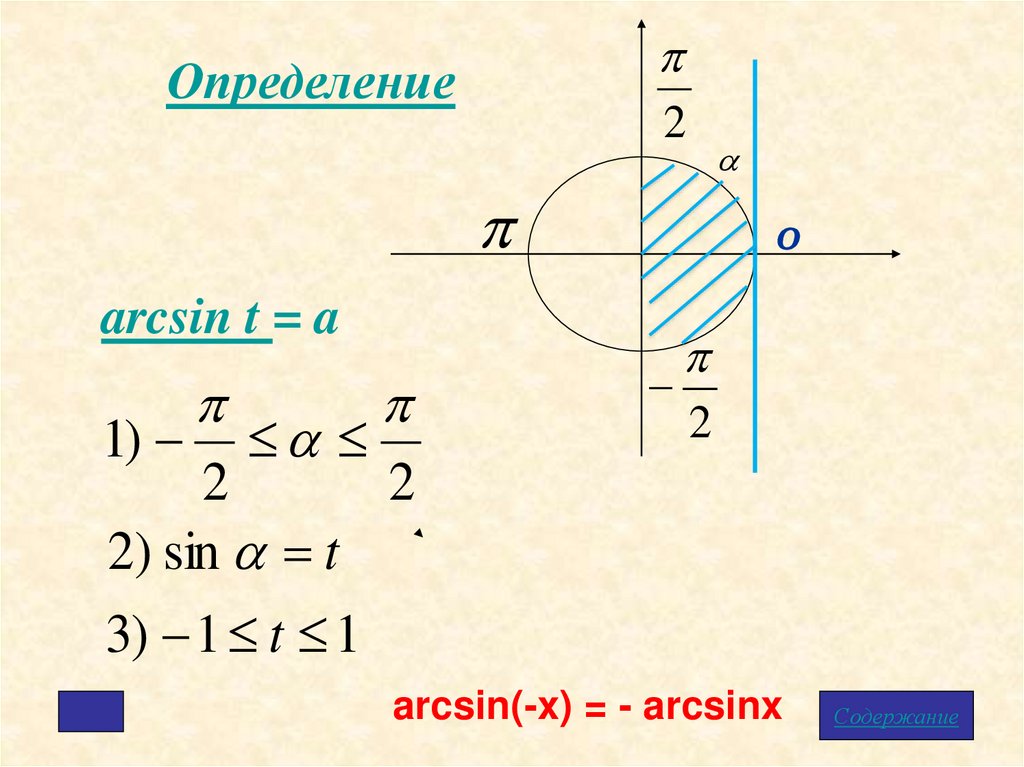
2
Определение
0
arcsin t = a
1)
2
2
2) sin t
3) 1 t 1
2
arcsin(-x) = - arcsinx
Содержание

8.

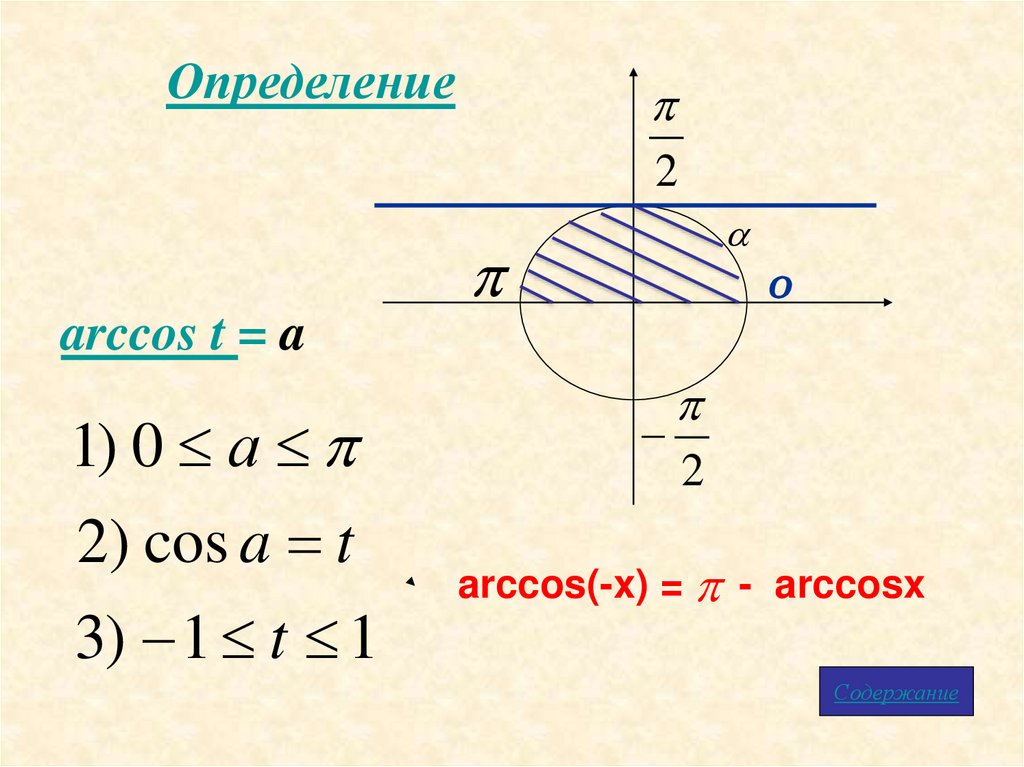
Определение
2
0
arccos t = a
1) 0 а
2) cos a t
3) 1 t 1
2
arccos(-x) = - arccosx
Содержание

9.

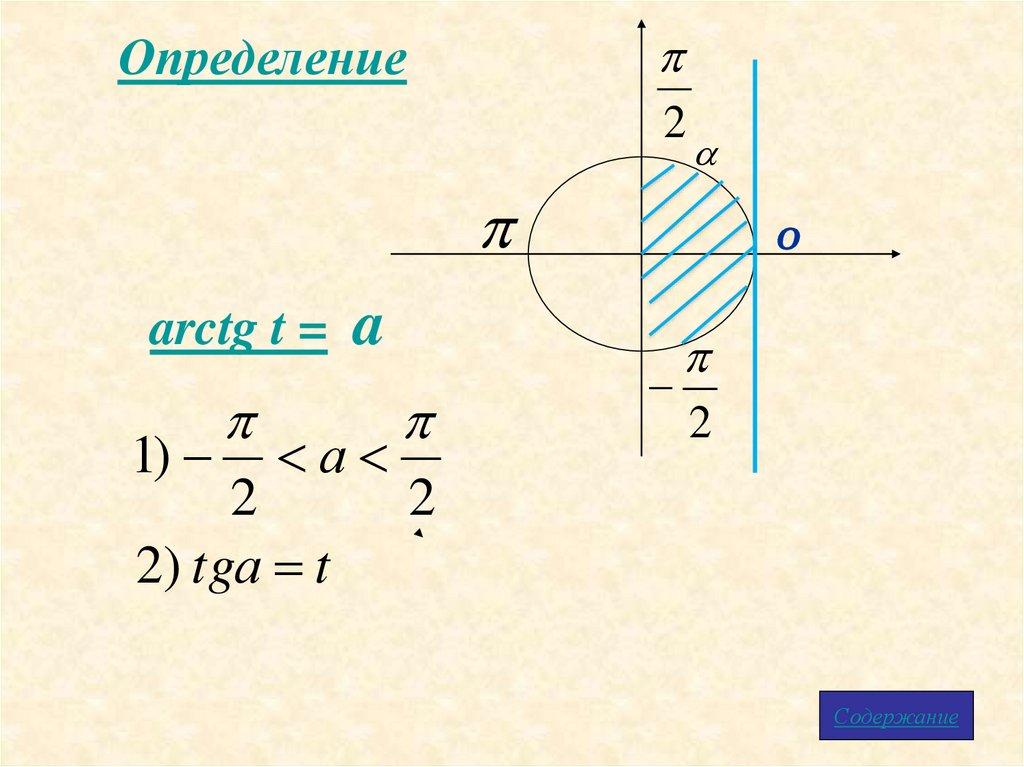
2
Определение
arctg t = a
1)
а
2
2) tgа t
0
2
2
Содержание

10.

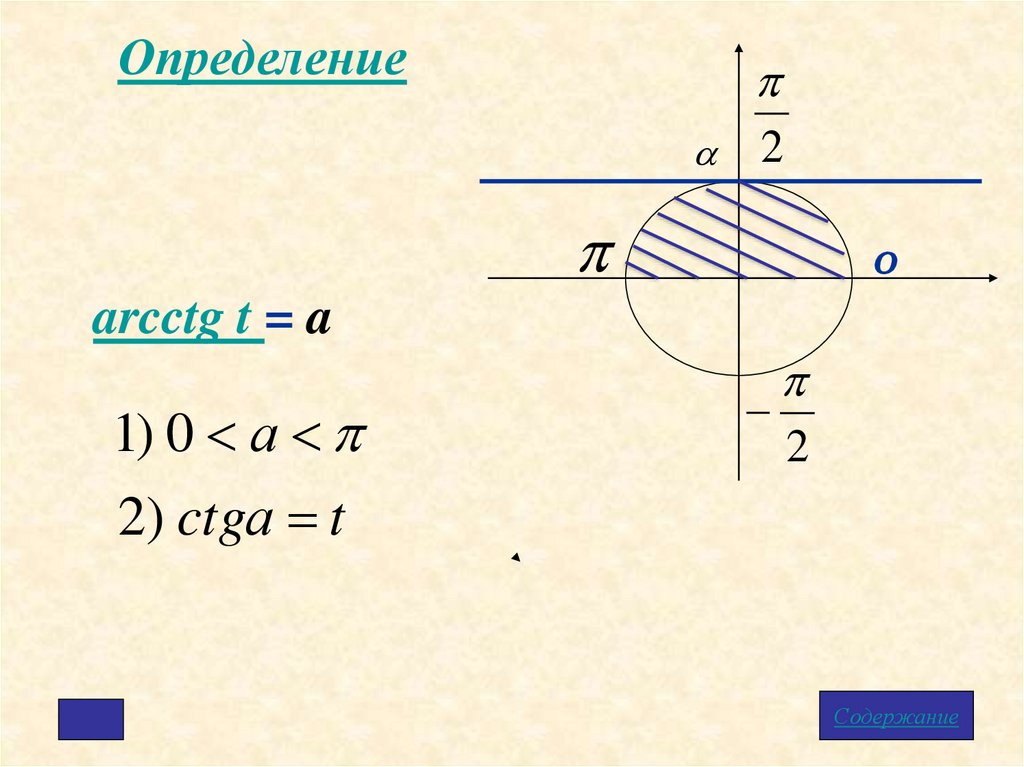
Определение
2
0
arcctg t = a
1) 0 а
2) ctgа t
2
Содержание

11.

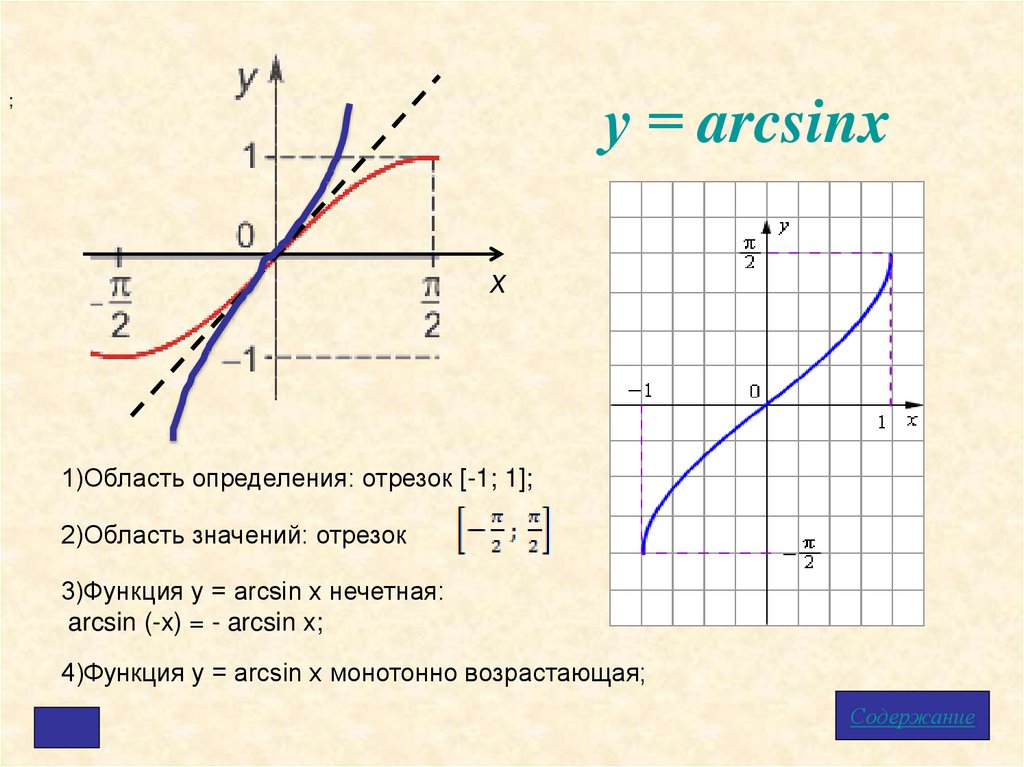
у = arcsinx
;
х
1)Область определения: отрезок [-1; 1];
2)Область значений: отрезок
3)Функция у = arcsin x нечетная:
arcsin (-x) = - arcsin x;
4)Функция у = arcsin x монотонно возрастающая;
Содержание

12.

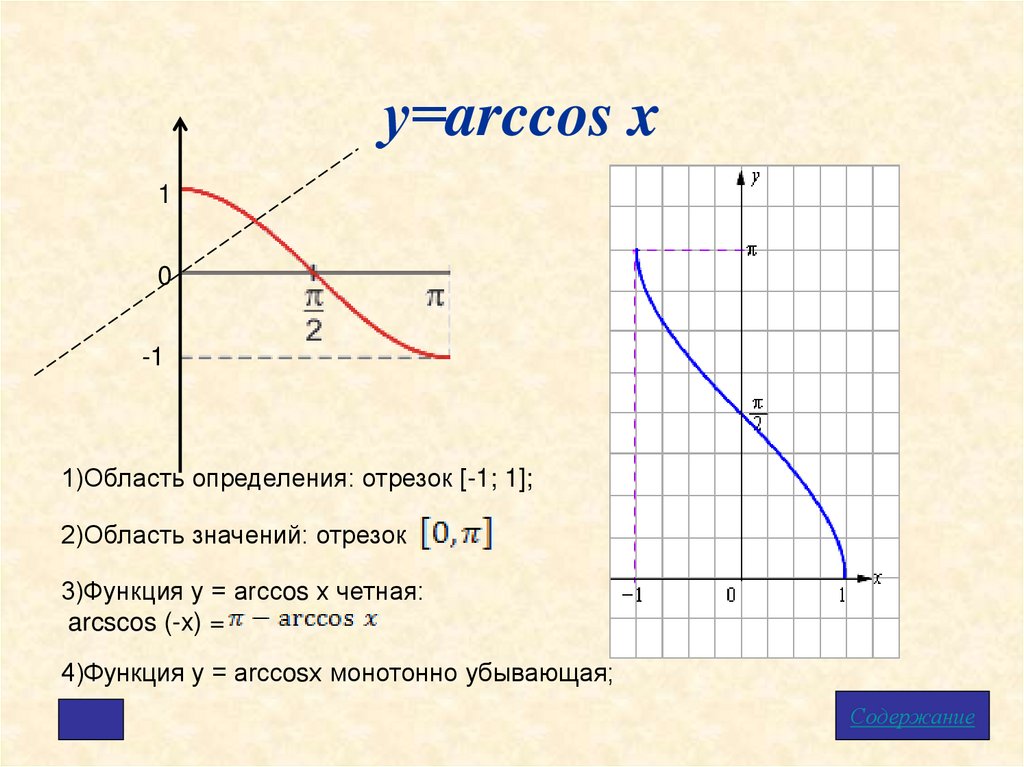
у=arccos x
1
0
-1
1)Область определения: отрезок [-1; 1];
2)Область значений: отрезок
3)Функция у = arcсos x четная:
arcscos (-x) =
4)Функция у = arcсosx монотонно убывающая;
Содержание

13.

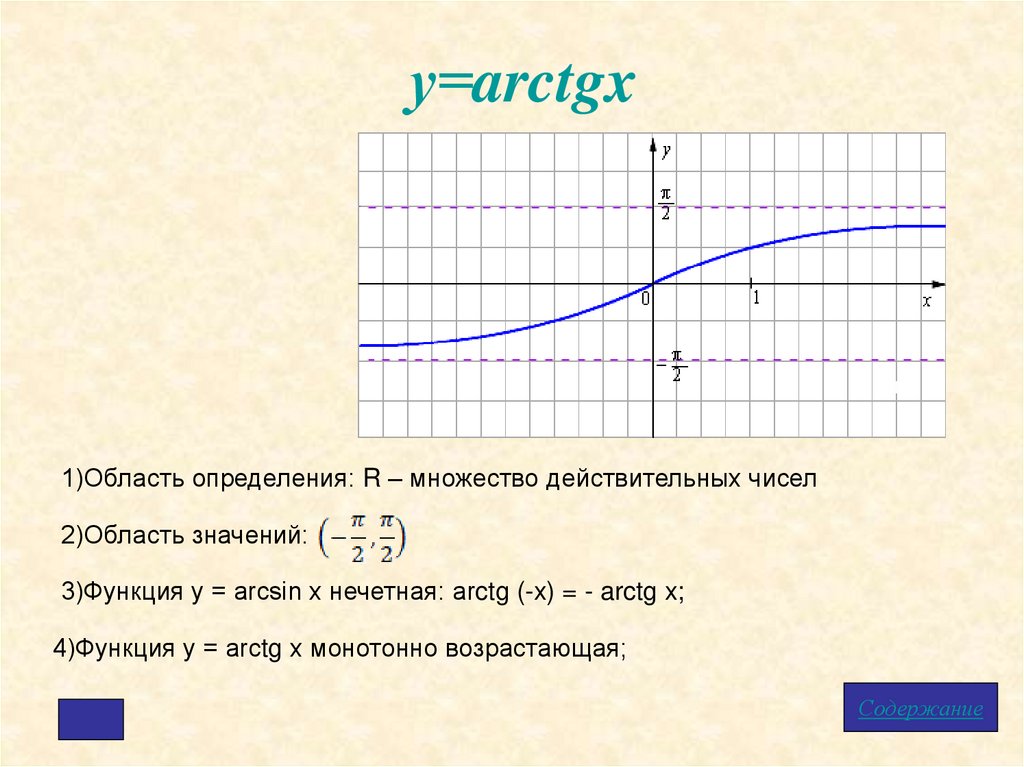
у=arctgx
1)Область определения: R – множество действительных чисел
2)Область значений:
3)Функция у = arcsin x нечетная: arctg (-x) = - arctg x;
4)Функция у = arctg x монотонно возрастающая;
Содержание

14.

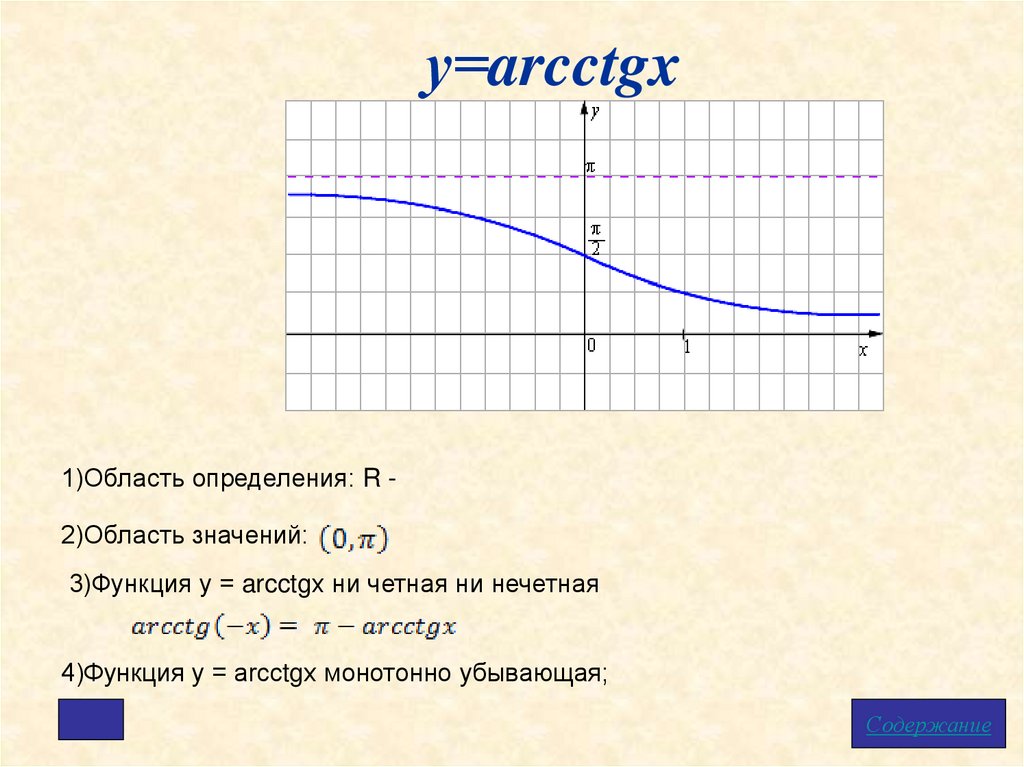
у=arcctgx
1)Область определения: R 2)Область значений:
3)Функция у = arcctgх ни четная ни нечетная
4)Функция у = arcсtgx монотонно убывающая;
Содержание

15.

16.

«Функция, как правило, определяется
для тех значений аргумента, какие для
данной задачи представляют реальное
значение»
Хинчин А.Я.

17.

•учащиеся должны знать определения арксинуса,
арккосинуса, арктангенса, арккотангенса, графики
этих функций, свойства аркфункций, связь с
тригонометрическими функциями уметь находить
значения обратных тригонометрических функций,
решать простейшие уравнения, содержащие
обратные тригонометрические функции
графическим и функционально-графическим
методом
•воспитывать ответственность, аккуратность при
построении графиков
•развивать логическое мышление, математическую
речь, умение работать в нужном темпе, внимание

18.

Работаем устно
arcsin 1
arcsin 0
arccos 1
arccos 0
2
arcsin
2
1
arcsin
2
1
arccos
2
1
arccos
3
arcsin(-x) = - arcsinx
1
arcsin( )
2
1
arccos( )
2
3
2
arcsin( )
arccos(
)
2
2
arccos(-x) = - arccosx
Содержание

19.

Работаем устно
Имеет ли смысл выражение?
arcsin 2 arccos 3
arctg100
Может ли arcsint и arccost принимать
значение равное
5
5, , , 10,
9
3
,?
7
Содержание

20.

Работаем устно
Найдите значения выражений:
arccos(cos )
3
5
arcsin(sin
)
2
7
ctg (arcctg ( ))
8
tg (arctg15)
5
sin(arcsin
)
13
3
cos(arcsin
)
2
Содержание

21.

Работаем устно
3
arctg1
arctg 3
arctg ( )
3
3
arcctg1 arcctg 3
arcctg ( )
3
arctg(-x) = - arctgx
arcctg(-x) = - arcctgx
Содержание

22.

Свойства аркфункций
cos(arccos x ) x,
sin(arcsin x) x,
tg ( arctgx) x
ctg ( arcctgx) x
arccos(cos x) x, x 1;1
arcsin(sin x) x, x 1;1
arctg (tgx) x,
arcctg (ctgx) x.

23.

24.

Формулы связывающие обратные
тригонометрические функции

25. Графический метод решения уравнений

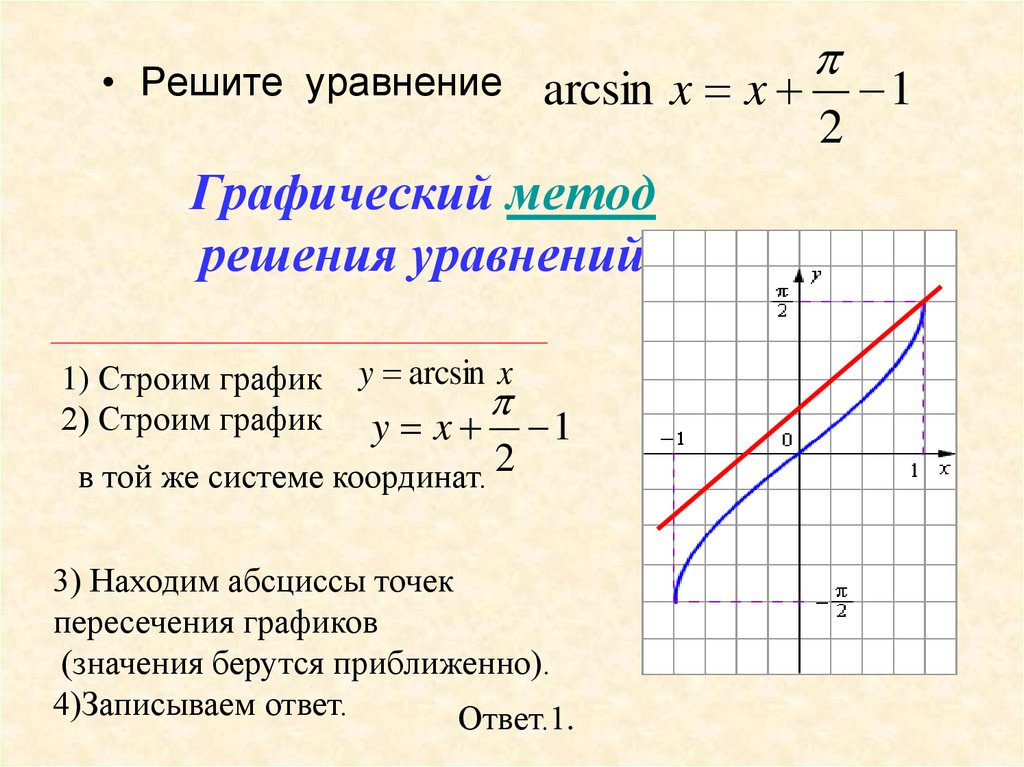
• Решите уравнение
arcsin x x
Графический метод
решения уравнений
1) Строим график
2) Строим график
y arcsin x
y x
в той же системе координат. 2
1
3) Находим абсциссы точек
пересечения графиков
(значения берутся приближенно).
4)Записываем ответ.
Ответ.1.
2
1

26.

Функционально-графический
метод решения уравнений
Пример: решите равнение
arccos x
Решение.
2
x
1) у =arccosx убывает на области определения
2 g x
x, возрастает на D,
2
3) Уравнение f(x)=g(x) имеет не более одного
корня.
4) Подбором находим, что x=0.
Ответ. 0.
Содержание

27. Спасибо за урок!

Успехов в дальнейшем
изучении тригонометрии!
Содержание