Similar presentations:
Обратные тригонометрические функции
1.
Обратныетригонометрические
функции
2.
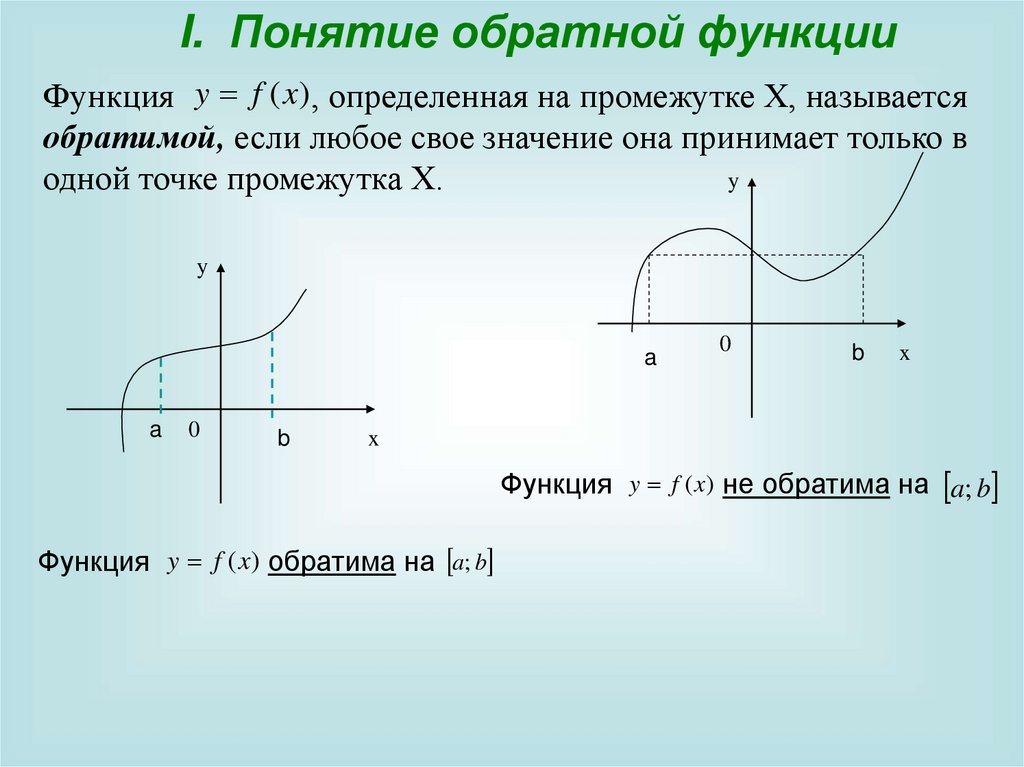
I. Понятие обратной функцииФункция y f (x) , определенная на промежутке Х, называется
обратимой, если любое свое значение она принимает только в
y
одной точке промежутка Х.
y
a
a
0
b
0
b
x
x
Функция y f (x) не обратима на a; b
Функция y f (x) обратима на a; b
3.
Теорема. Если функция y f (x) строго монотонна на промежутке Х, то онаобратима на этом промежутке.
Доказательство.
Пусть функция y f (x) возрастает на Х, тогда по определению
возрастающей функции
x1 , x2 : x1 x2 f ( x1 ) f ( x2 )
т.о. различным значениям аргумента соответствуют различные значения
функции, т.е. функция обратима.
4.
Пусть обратимая функция y f (x) определена на промежутке Х, аобластью значений ее является промежуток Y. Поставим в соответствие
каждому y Y то единственное значение x X , при котором y f (x.)
Тогда получим функцию, которая обозначается
x f 1 ( y )
и называется обратной по отношению к функции y f (x)
.
Обычно для обратной функции делают переход к привычным обозначениям,
т.е. аргумент обозначают буквой х, а значение функции y.
Поэтому вместо x f
1
( y ) пишут y f 1 ( x)
Замечание. Графики взаимообратных функций симметричны относительно
прямой y x
5.
Алгоритм получения обратной функции1) Убедиться в том, что функция
2) Из уравнения y f (x)
y f (x) обратима на Х.
выразить х через y.
3) В полученном равенстве поменять местами х и y.
Свойства обратной функции
1
1
D
(
f
)
E
(
f
);
E
(
f
)
D
(
f
)
1)
;
2) Если функция y f (x) возрастает (убывает) на
y f 1 ( x) возрастает (убывает) на D( f 1 ) ;
3)
f 1 ( f ( x)) x, x D( f )
D ( f ) , то и функция
6.
Обратныетригонометрические
функции
7. Тест 10 минут
КритерииОценка «5» - 5 баллов
Оценка «4» - 4 балла
Оценка «3» - 3 балла
Оценка «2» - 2 и менее баллов
8.
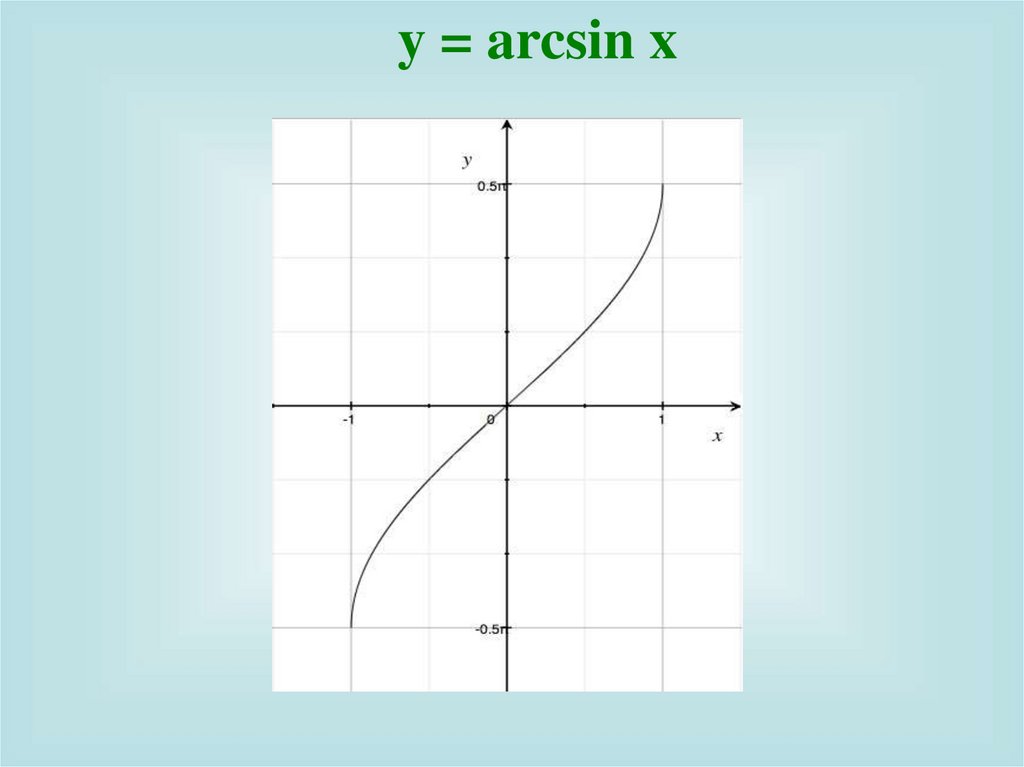
y = arcsin x9.
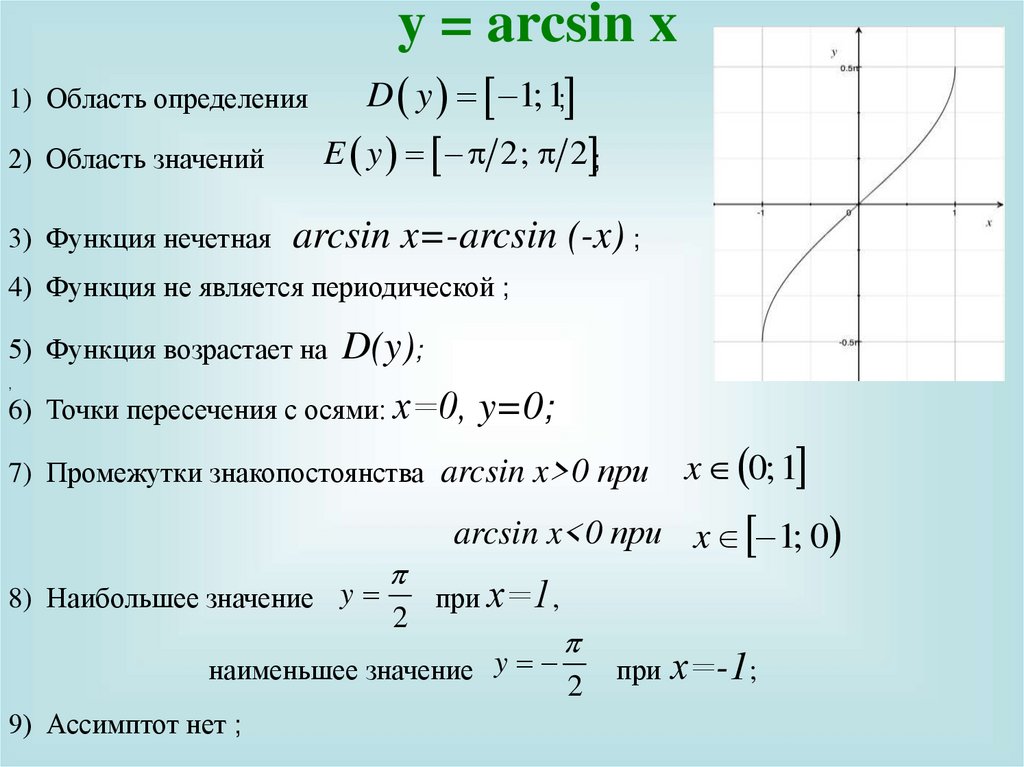
y = arcsin x1) Область определения
D y 1; 1;
2) Область значений
E y 2; 2 ;
3) Функция нечетная
arcsin x=-arcsin (-x) ;
4) Функция не является периодической ;
5) Функция возрастает на D(y);
,
6) Точки пересечения с осями: х=0, y=0;
7) Промежутки знакопостоянства arcsin x>0 при
8) Наибольшее значение y
2
arcsin x<0 при x 1; 0
при х=1,
наименьшее значение y
9) Ассимптот нет ;
x 0; 1
2
при х=-1;
10.
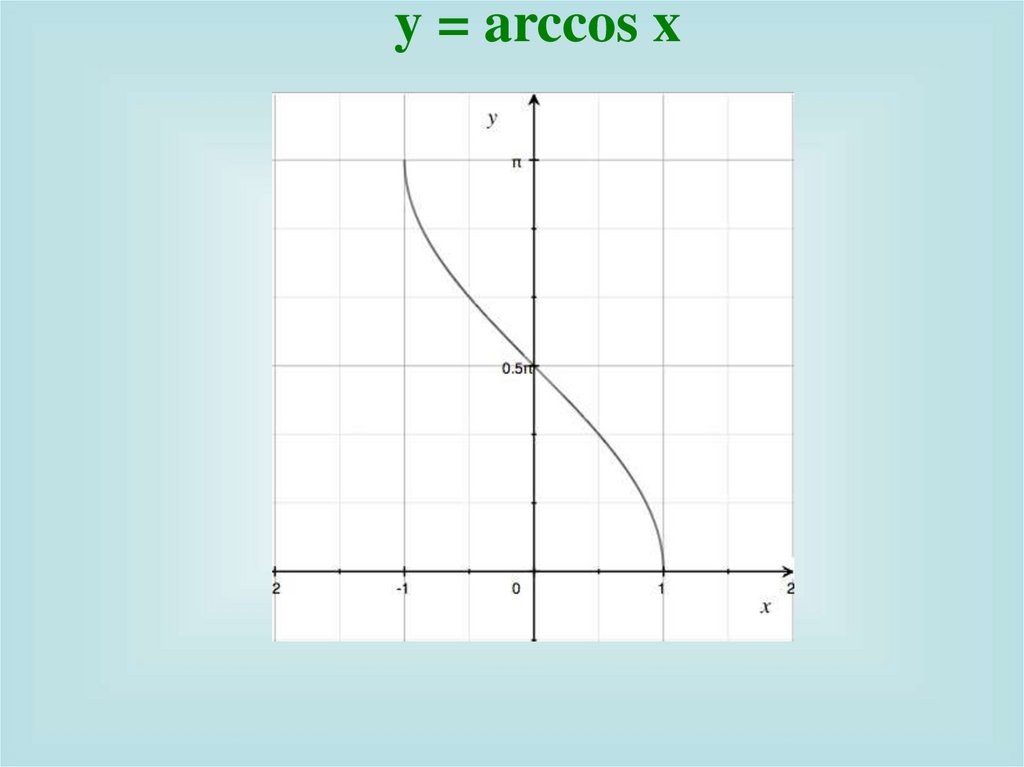
y = arccos x11.
y = arccos x1) Область определения
2) Область значений
D y 1; 1;
E y 0;
;
3) Функция не обладает определенной четностью;
4) Функция не является периодической ;
5) Функция убывает на D(y);
,
6) Точки пересечения с осями: 1) х=0, y
2
; 2) y=0, x=1
7) Промежутки знакопостоянства arccos x>0 при x [ 1;1]
8) Наибольшее значение
y при х=-1,
наименьшее значение y=0 при х=-1;
9) Ассимптот нет .
12.
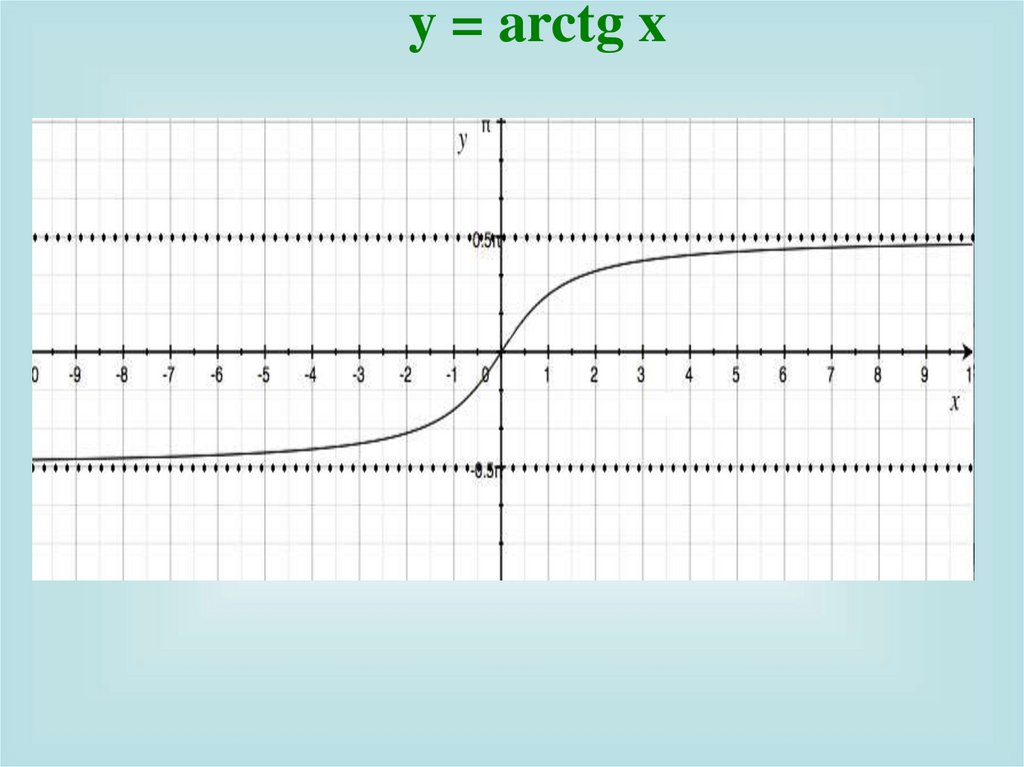
y = arctg x13.
y = arctg x1) Область определения D(y)=R ;
2) Область значений
E y 2; 2 ;
3) Функция нечетная arctg x=-arcctg (-x) ;
4) Функция непериодическая ;
5) Функция возрастает на D(y);
,
6) Точки пересечения с осями: х=0, y=0;
7) Промежутки знакопостоянства arctg x>0 при
x 0;
arctg x<0 при x ;0
8) Наибольшего и наименьшего значений не существует ;
9) Горизонтальные асимптоты y
2
;
14.
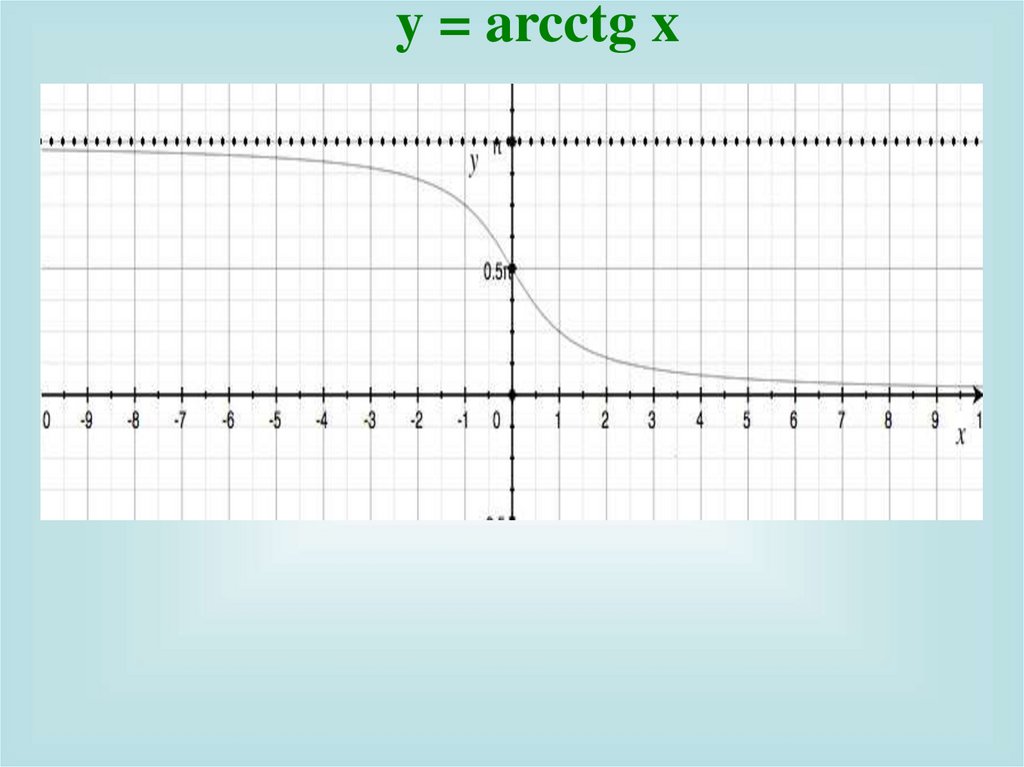
y = arcctg x15.
y = arcсtg x1) Область определения D(y)=R ;
2) Область значений
E y 0; ;
3) Функция не имеет определенной четности ;
4) Функция непериодическая ;
5) Функция убывает на D(y);
,
6) Точки пересечения с осями: х=0, y
2
;
7) Промежутки знакопостоянства arcсtg x>0 при
x R ;
8) Наибольшего и наименьшего значений не существует ;
9) Горизонтальные асимптоты y 0;
y .
16.
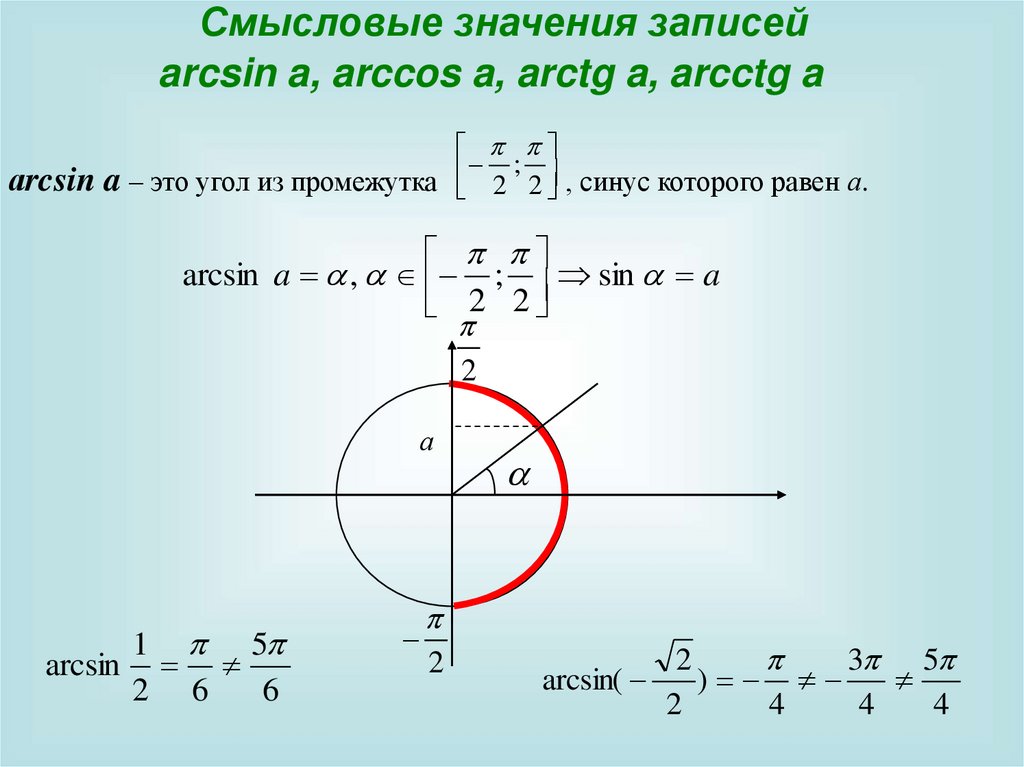
Смысловые значения записейarcsin a, arccos a, arctg a, arcctg a
;
аrcsin a – это угол из промежутка 2 2 , синус которого равен а.
arcsin a , ; sin a
2 2
2
а
1 5
arcsin
2 6
6
2
2
3 5
arcsin(
)
2
4
4
4
17.
Смысловые значения записейarcsin a, arccos a, arctg a, arcctg a
0; , косинус которого равен а.
arccos a , 0; cos a
аrccos a – это угол из промежутка
1
2 4
arccos( )
2
3
3
а
0
arccos
3
2
6
6
18.
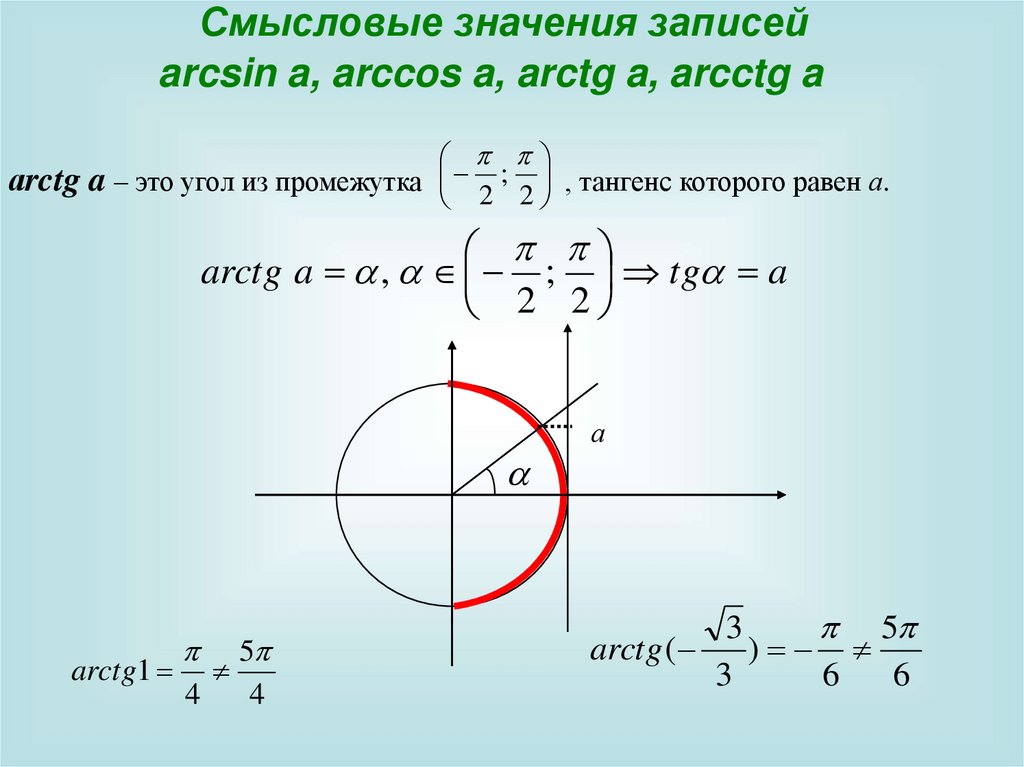
Смысловые значения записейarcsin a, arccos a, arctg a, arcctg a
аrctg a – это угол из промежутка 2 ; 2 , тангенс которого равен а.
arctg a , ; tg a
2 2
arctg1
4
5
4
а
arctg (
3
5
)
3
6
6
19.
Смысловые значения записейarcsin a, arccos a, arctg a, arcctg a
аrcсtg a – это угол из промежутка
0; , котангенс которого равен а.
arcctg a , 0; ctg a
а
arcctg1
4
3
4
arcctg (
3
2
)
3
3
3
20.
Основные свойства обратныхтригонометрических функций
arcsin x arcsin x
arctg x arctgx
arccos x arccos x
arcctg x arcctgx
arcsin x arccos x
2
arctgx arcctgx
2
21.
22.
23.
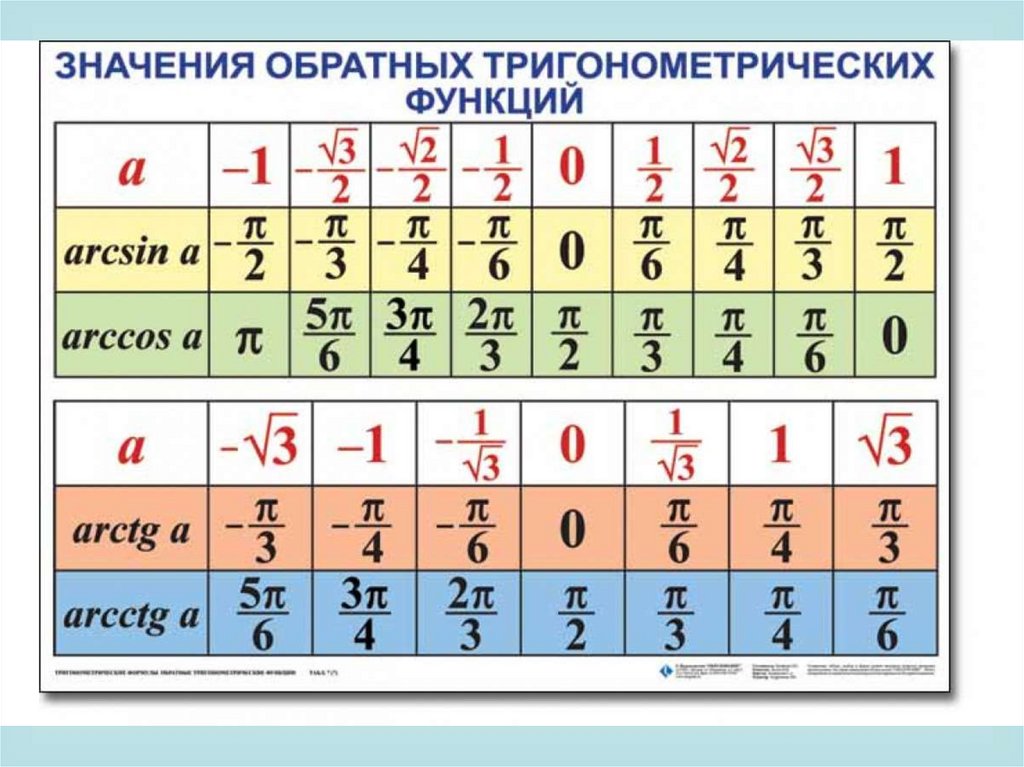
Формулы связывающие обратныетригонометрические функции














 mathematics
mathematics








