Обратные тригонометрические функции

1.

Урок по теме:
«Обратные
тригонометрические
функции»
1

2.

сos х = а, -1≤а≤1
х= ± arccos а+2 πn , n €Z
arccos а = α, сos α = а
-1≤а≤1, 0 ≤α≤ π
arccos (-а)= π- arccos а
2

3.

sin х = а, -1≤а≤1
х = (-1)ⁿ arcsin а+ πn , n €Z
arcsin а = α, sin α= а
-1≤а≤1, - π/2 ≤α≤ π/2
аrcsin(-а)= - arcsin а
3

4.

tg х = а
х= аrctg а + πn , n €Z
аrctg а = α, tg α = а
- π/2 <α< π/2
аrctg(- а)= - аrctg а
4

5.

сtg х = а
х= аrcсtg а + πn , n €Z
аrcсtg а = α, сtg α = а
0 <α< π
аrcсtg(- а)= π - аrcсtg а
5

6.

Таблица значений:
0
½
√3
2
0
π/6
π/3
π/4
π/2
π/2
π/3
π/6
π/4
0
arcsin x
arccos x
arctg x
arcctg x
√2
2
√3
1
√3
1
0
π/3
π/6
π/4
π/2
π/6
π/3
π/4
6

7.

1)arcsin(1/√2) – arcsin 1= -7π/4
2)arccos(-1) – arcsin(-1) = 3π/2
3)4 arctg(-1) + 3 arctg(√3) = 0
4)arcsin(sin π/3) +arcsin( √3/2)
=0
5)log (arccos (-1/2) –
arctg(√3)) =1
6)10 cos (arctg(√3)) = 5
7

8.

арксинус
• sin(arcsin a)=a, -1≤a≤1
• arcsin (sin α ) = α , - π/2 ≤α≤ π/2
• сos (arccos а ) = а , -1≤а≤1
арккосинус • arccos (сos α)= α, 0 ≤α≤ π
арктангенс
• tg(arctg a)= а
• arctg (tg α)= α, - π/2 < α < π/2
8

9.

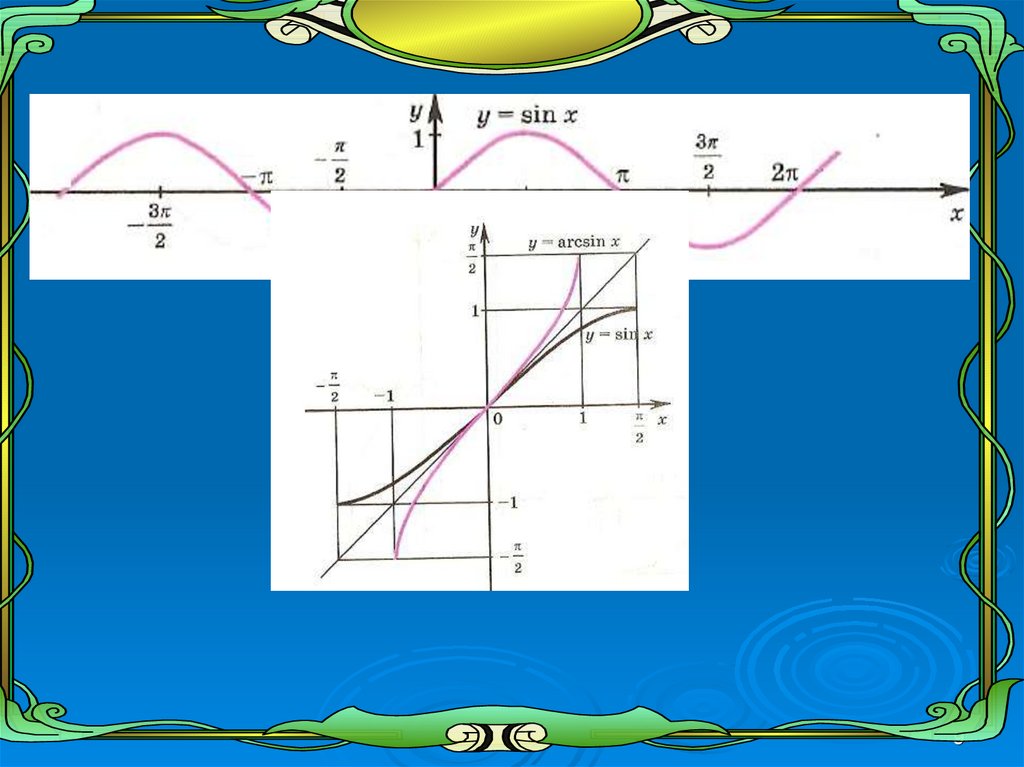
График функции у=sin х
9

10.

Функция y=arcsin x.
Определение:
Функция y=arcsin x есть
угол (дуга) α такой, что
х =sin α и –π/2≤х≤π/2.
10

11.

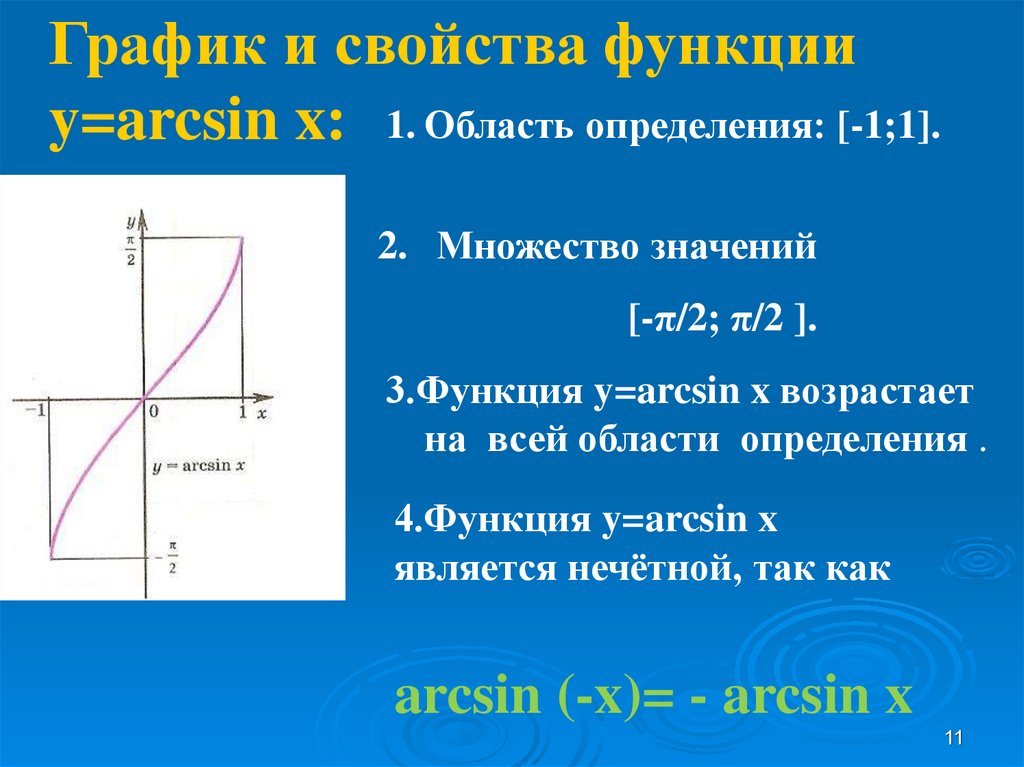
График и свойства функции
y=arcsin x: 1. Область определения: [-1;1].
2. Множество значений
[-π/2; π/2 ].
3.Функция y=arcsin x возрастает
на всей области определения .
4.Функция y=arcsin x
является нечётной, так как
arcsin (-x)= - arcsin x
11

12.

График функции у=cos х.
12

13.

Функция y=arcсоs x.
Определение:
Функция у= arcсоs x есть
угол α такой, что 0≤α≤π и
соs α = х.
13

14.

График и свойства функции
у= arcсоs x:
1. Область определения -[-1;1].
2.Множество значений –
[0; π ].
3.Функция у= arcсоs x
убывает на всей
области определения.
аrcсоs(- x)= π-arcсоs x
14

15.

Функция у = arctg x.
Определение:
Функция у = arctg x
есть угол α такой, что
- π/2 < α< π/2, tg α = х.
15

16.

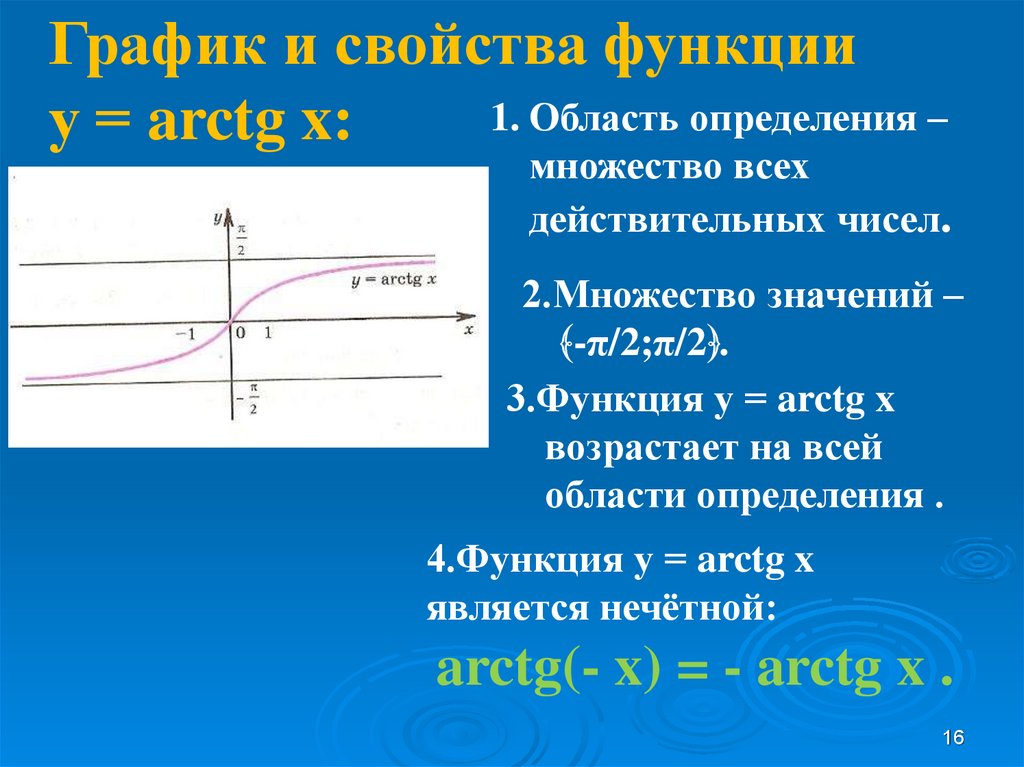
График и свойства функции
1. Область определения –
у = arctg x:
множество всех
действительных чисел.
2.Множество значений –
-π/2;π/2 .
3.Функция у = arctg x
возрастает на всей
области определения .
4.Функция у = arctg x
является нечётной:
arctg(- x) = - arctg x .
16

17.

Функция у = arcсtg x.
Определение:
Функция у= arcсtg x
есть угол α такой, что
0<α<π и сtg α = х.
17

18.

График и свойства функции
1. Область определения –
у= arcсtg x:
множество всех
действительных чисел.
2.Множество значений –
0;π .
3.Функция у = arcсtg x
убывает на всей области
определения .
arcсtg(- x) = π- arcсtg x .
18

19.

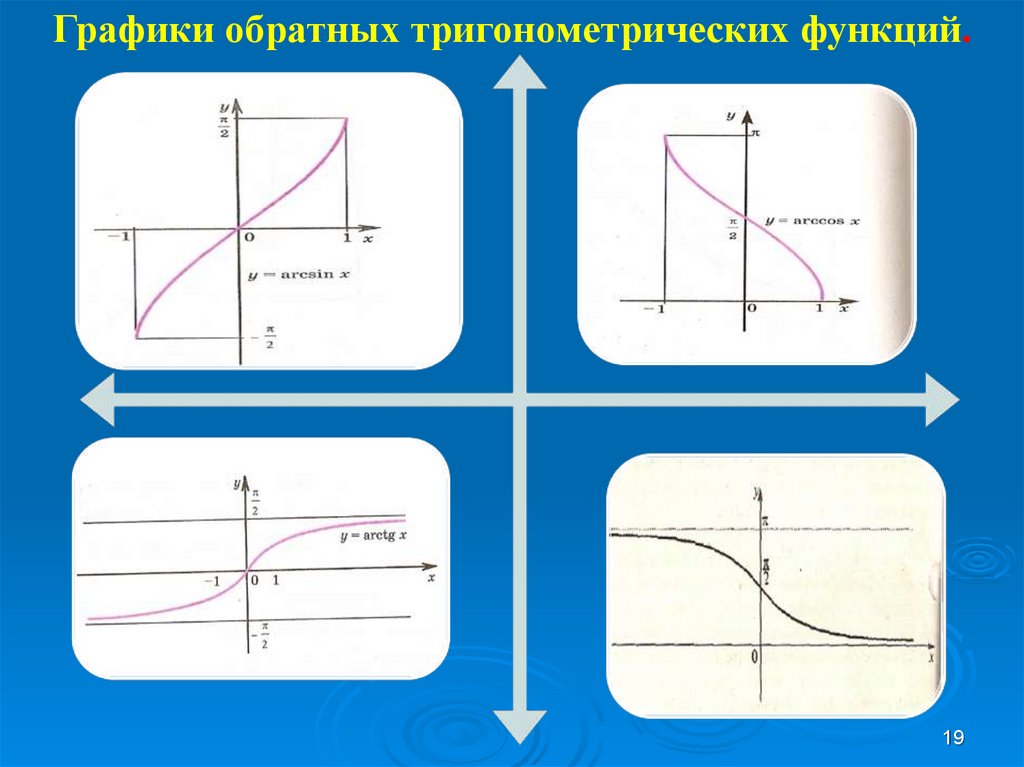
Графики обратных тригонометрических функций.
19

20.

Тестовая проверочная работа:
1 вариант
2 вариант
1.Вычислите: sin(arcsin ⅓)
11) ⅓
2)-⅓ 3)π-⅓
4) π+⅓
1.Вычислите:arccos (cos (-¼))
1)
3) π-¼
4) π+¼
1 -¼ 2) ¼
2.Вычислите: cos(arcsin(- ½))
1)
2)- √3
3) - ½
4) ½
1 √3
2
2
2.Вычислите: sin(arccos(- ½))
1) - ½ 2) ½ 33)√3
4)- √3
2
2
3.Найдите число целых
значений функции: у= 8∙arcсоs x.
1)8
2)9
3)25
44)26
3.Найдите число целых
значений функции: у = 12∙arctg x.
4
1)13
2)12 3)39
4)37
4.Вычислите: tg(arcsin ⅓).
1.√13/4 2.1/2 33.1/(√8) 4. √8
4.Вычислите: сtg(arccos⅓).
1.√13/4 2.1/2 3.1/(√8)
4. √8
3
Критерии оценки: 1-2 верно выполненных задания – «3»
3 верно выполненных задания – «4»
4 верно выполненных задания – «5»
20

21.

Спасибо за
работу
21