Similar presentations:
Обратные функции. Свойства взаимно обратных функций
1. Обратные функции. Свойства взаимно обратных функций.
y f (x) ух
Обратные функции.
Свойства взаимно
обратных функций.
2. Основные вопросы:
1.Функция у = arcsin x, её свойстваи график.
2. Функция y = arсcos x, её
свойства и график.
3. Функция y= arctgx, её свойства
и график.
4. Функция y=arcctg x, её свойства
и график.
3.
22
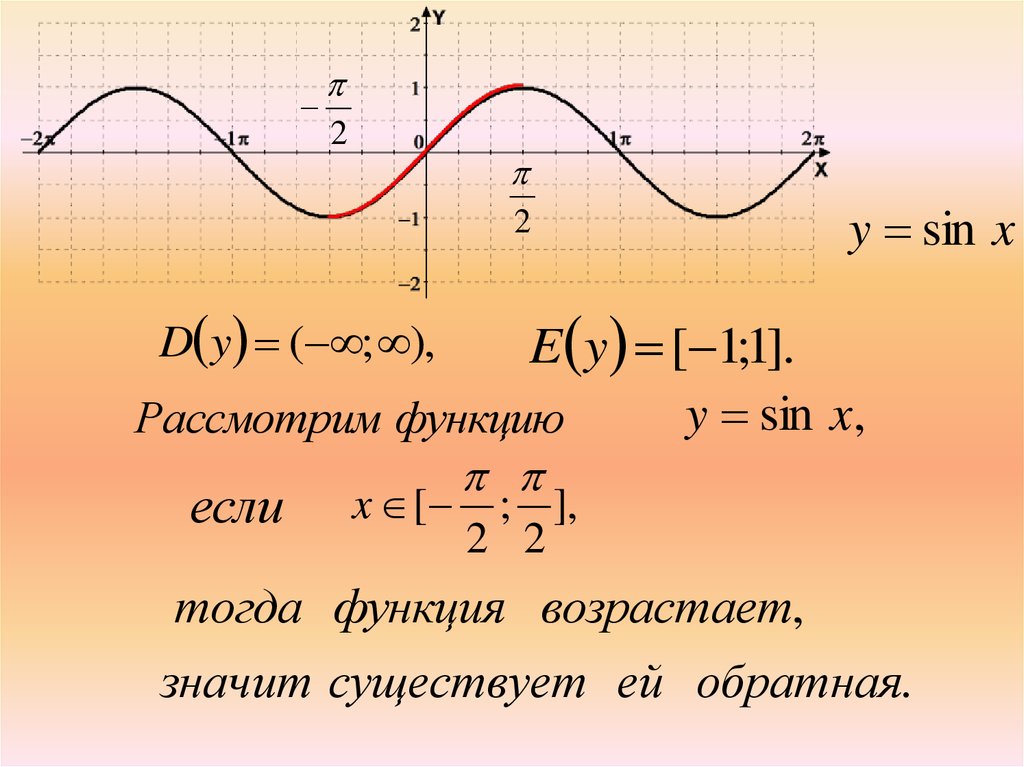
y sin x
E y [ 1;1].
y sin x,
Рассмотрим функцию
D y ( ; ),
если
x [
; ],
2 2
тогда функция возрастает,
значит существует ей обратная.
4.
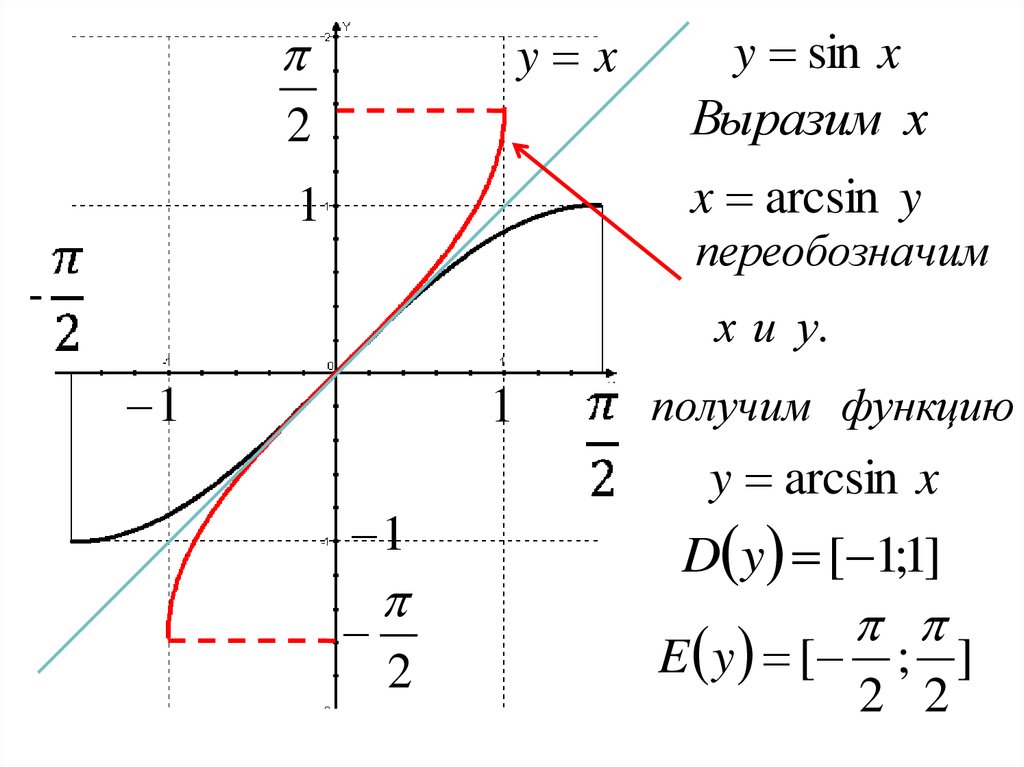
2y sin x
Выразим х
1
x arcsin y
y x
переобозначим
х и у.
1
1
1
2
получим функцию
y arcsin x
D y [ 1;1]
E y [ ; ]
2 2
5. Функция, обратная функции sin x
• Арксинусом числа а называется число b из [-П/2;П/2] такое, что
sin b = a.
Обозначение: arcsin b = a.
• D (arcsin х) = [-1;1]
• Е (arcsin х) = [-П/2; П/2]
• Функция у = arcsin х нечет ная arcsin (-х) = - arcsin х
• Функция у = arcsin х непрерывная на [-1;1]
• Функция у= arcsinх возраст ает на области
определения
• График функции у= arcsin х симмет ричен части
графика у= sin х при хЄ [-П/2; П/2 ] относительно
прямой у = х
6.
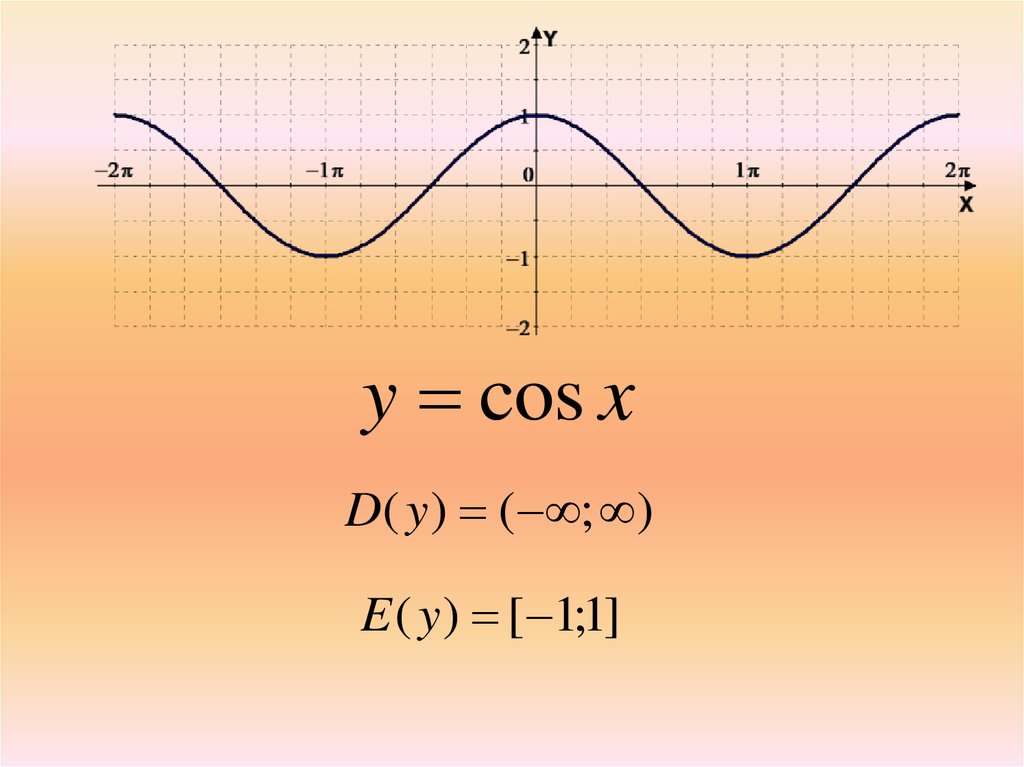
y cos xD( y ) ( ; )
E ( y ) [ 1;1]
7.
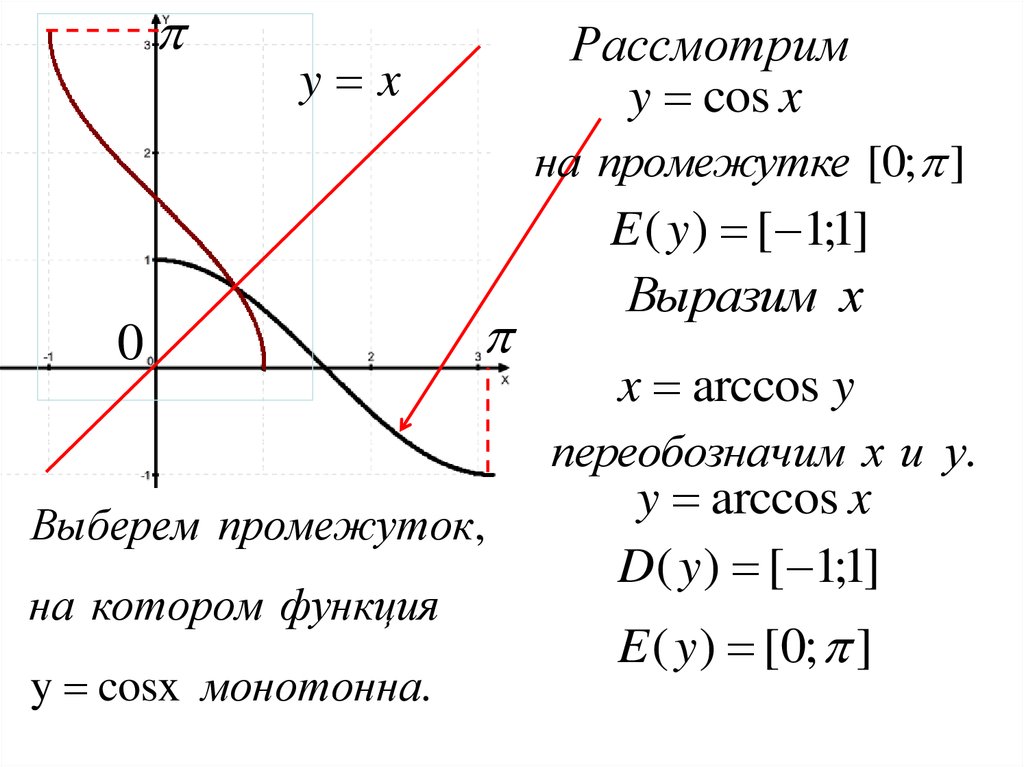
Рассмотримy cos x
y x
на промежутке [0; ]
0
E ( y ) [ 1;1]
Выразим х
x arccos y
переобозначим х и у.
Выберем промежуток,
на котором функция
y cosx монотонна.
y arccos x
D( y ) [ 1;1]
E ( y ) [0; ]
8. Функция, обратная функции cos x
• Арккосинусом числа а называется число b из [-1; 1]такое, что соs b = a
• Обозначение: arcсоs b = a
• D (arcсоs х)=[-1; 1]
• Е (arcсоs х)= [0; П]
• Функция у = arcсоs х не является четной и нечетной
arcсоs (-х)= П -arcсоs х
• Функция у = arcсоs х непрерывная на [-1;1]
• Функция у = arcсоs х убывает на области
определения
• График функции у = arcсоs х симметричен части
графика у = соs х при хЄ [0; П] относительно
прямой у = х
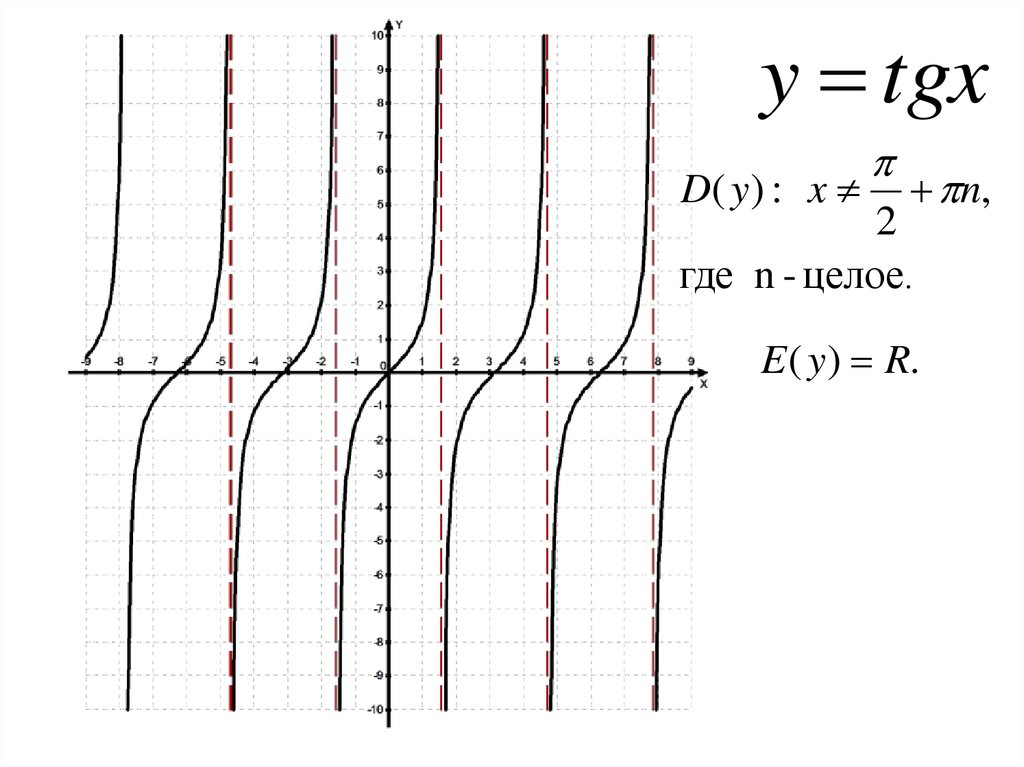
9.
y tgxD( y ) : x
n,
2
где n - целое.
E ( y ) R.
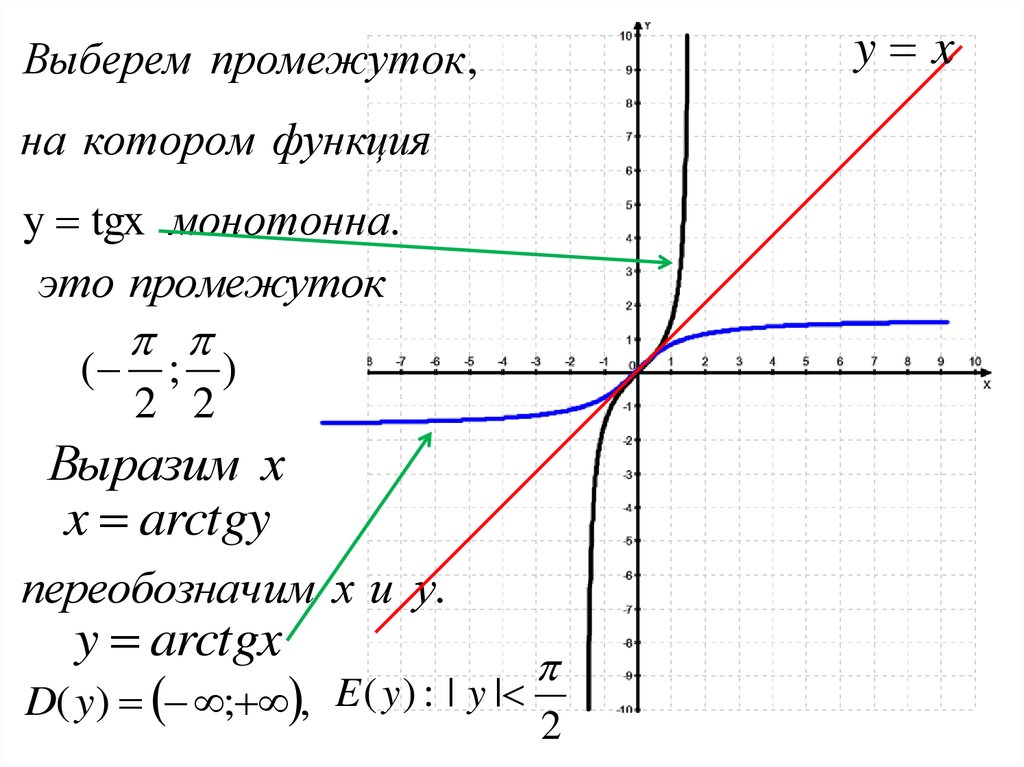
10.
y xВыберем промежуток,
на котором функция
y tgx монотонна.
это промежуток
( ; )
2 2
Выразим х
x arctgy
переобозначим х и у.
y arctgx
D( y) ; , E ( y ) : | y |
2
11. Функция, обратная функции tg x
• Арктангенсом числа а называется число b из(-П/2; П/2) такое, что tg b = a
Обозначение: arctg b = a.
• D (arctg х) = R
• Е (arctg х) = (-П/2; П/2)
• Функция у = arctg х нечет ная arctg (-х) = arctg х
• Функция у = arctg х возраст ает на области
определения
• График функции у = arctg х cиммет ричен
части графика у= tg х при хЄ (-П/2; П/2)
относительно прямой у = х
12.
у2
-1
π
_
0
1
х
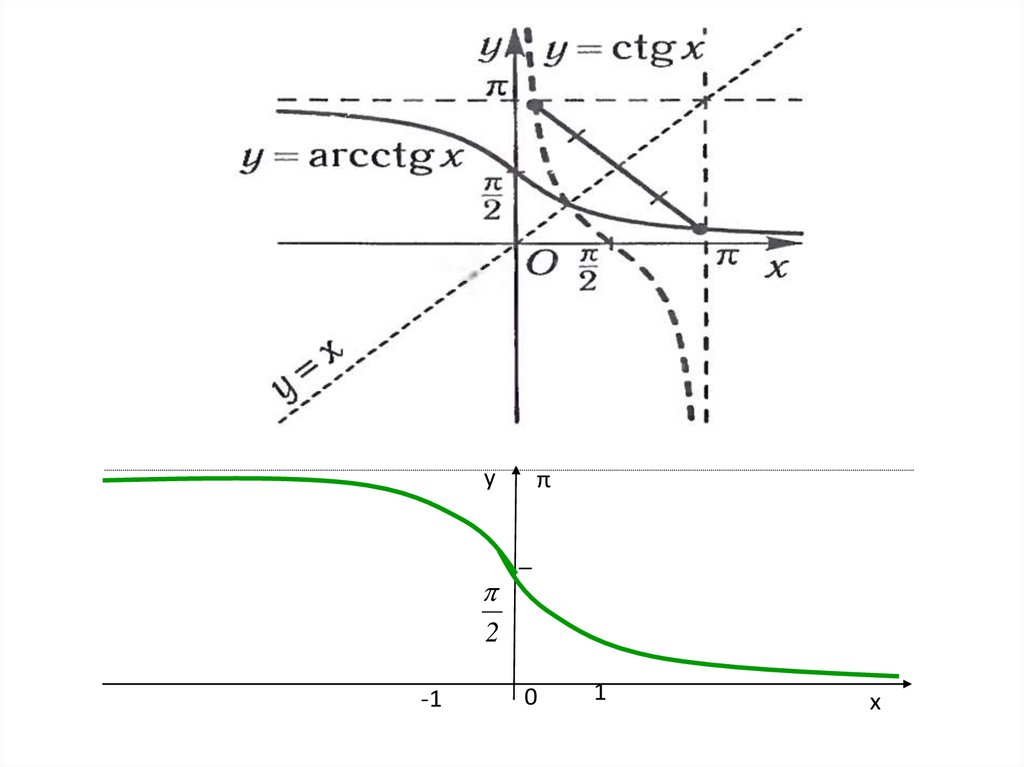
13. Функция, обратная функции ctg x
• Арккотангенсом числа а называется число bиз (0;П) такое, что сtg b = a
Обозначение: arcсtg b = a.
• D (arсctg х) = R
• Е (arсctg х) = (0; П)
• Функция у = arсctg х не является четной и
нечетной
arсctg (-х)= = П - arcсtg х
• Функция у = arсctg х убывает на области
определения
• График функции у = arсctg х cимметричен
части графика у= сtg х при хЄ (0; П)
относительно прямой у = х
14.
15.
16.
17.
18.
19.
Преобразование выраженийВычислить :
3tg arcsin 0,5 ;
1) 24
2) 4
2 cos arcctg1 ;
3
7 ctg
arcsin
.
4
Решение :
3) 12
1) 24
3tg
2) 4
2 cos
6
24
3
1
24.
3
4
2
2
4.
2
4
3
3) sin - , cos 1 sin
4
ctg
12
2
1
7
,
3
3
7 ctg
arcsin
12
4
12
9
7
,
16
4
7 (
7
) 28.
3
3
7 ctg
arcsin
4
20.
Уравнения, содержащиеобратные тригонометрические функции
1.Решить уравнение arccos(2x 1)
3
.
4
3
0; , тт по определению арккосинус а
4
числа данное уравнение равносильно уравнению
Так как
3
2
2 2
, откуда 2x 1 ,x
.
4
2
4
2.Решить уравнение 2(arcsinx) 2 5 arcsin x 2 0.
2x 1 cos
Пусть arcsinx t, причем t ;
, тогда
2 2
2t 2 5t 2 0.
1
, но 2 ;
,
2
2 2
1
1
arcsinx
, x sin
.
2
2
t 1 2, t 2















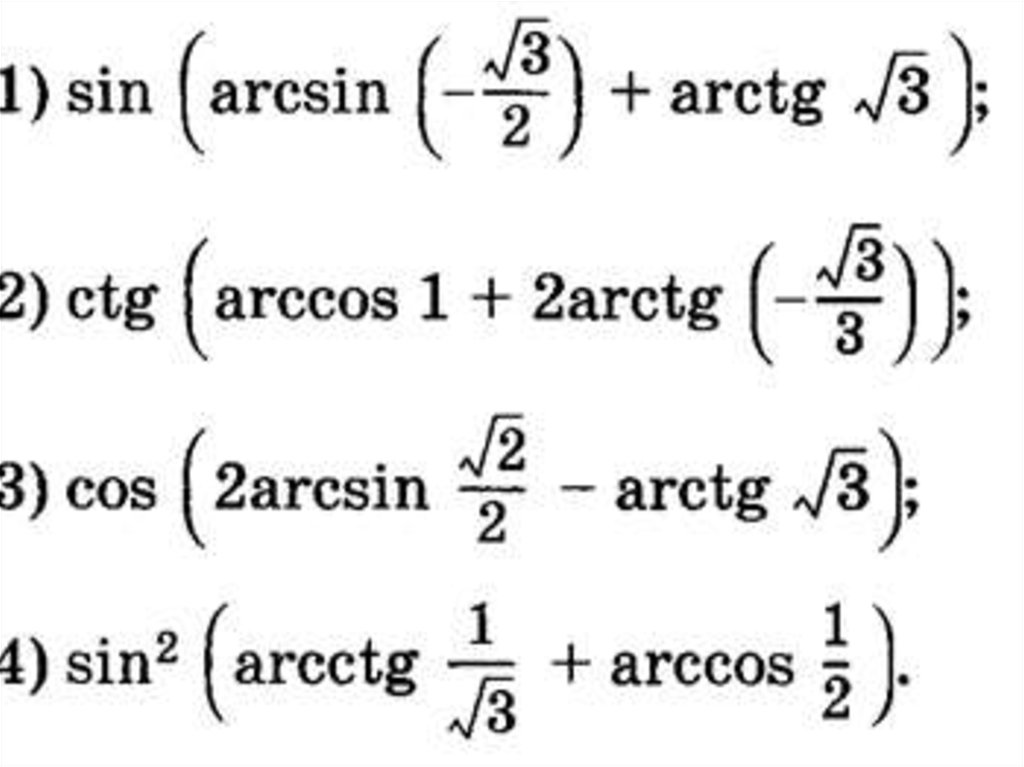
 mathematics
mathematics








