Similar presentations:
Колебания. Лекция № 1
1.
Лекция № 1Колебания
2.
ЛитератураТ. И. Трофимова. Курс физики
§§140 – 148;
А. А. Детлаф, Б. М. Яворский.
Курс физики гл. 27, 28.
Н. П. Калашников,
Н. М. Кожевников,
4 ДЕ, задания 17 – 20.
3.
Колебания- процессы, повторяющиеся во
времени, их тип определяет
природа процесса.
Различают колебания:
механические,
электромагнитные,
электромеханические и другие.
4.
КолебанияПериодические
- повторяются
через равные промежутки
времени.
Гармонические - описываются
законом синуса или косинуса.
5.
Механические колебанияОпыт Кавендиша
5
6.
Механические колебанияПри абсолютно упругом ударе шаров
(нет потерь энергии) скорость и угол
отклонения
крайних
шаров
одинаковы, промежуточные шары - в
покое.
6
7.
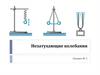
Движение шарика (без трения)Закон
Гука:
Fу kxi
i
0
Х
Fвн- внешняя сила,
Fв- внутренняя сила (упругости)
8.
Механические колебанияМТ
xm
x
0
X
xm
x xm sin t 0
- координата (смещение) МТ
в момент времени t;
xm - максимальное смещение
(амплитуда колебаний);
9.
Механические колебанияМТ
xm
0
xm
x
X
0
x xm sin t 0
0 0
t
- циклическая частота;
0 - начальная фаза колебаний;
t 0 - фаза колебаний;
10.
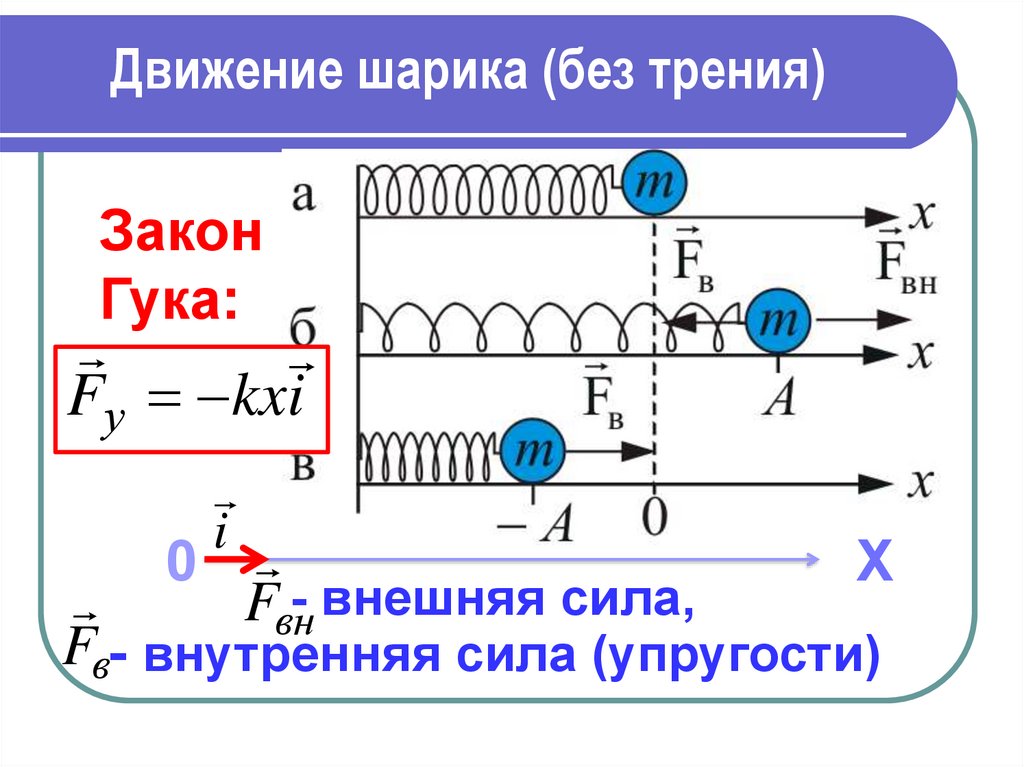
x A cosφТ – период колебаний,
φ – фаза колебаний,
А – амплитуда колебаний.
11.
Скорость и ускорениеdx
x x xm sin t 0
dt
xm cos t 0 m cos t 0
скорость МТ, совершающей ГК;
a x x xm sin t 0
2
am sin t 0 ускорение МТ.
12.
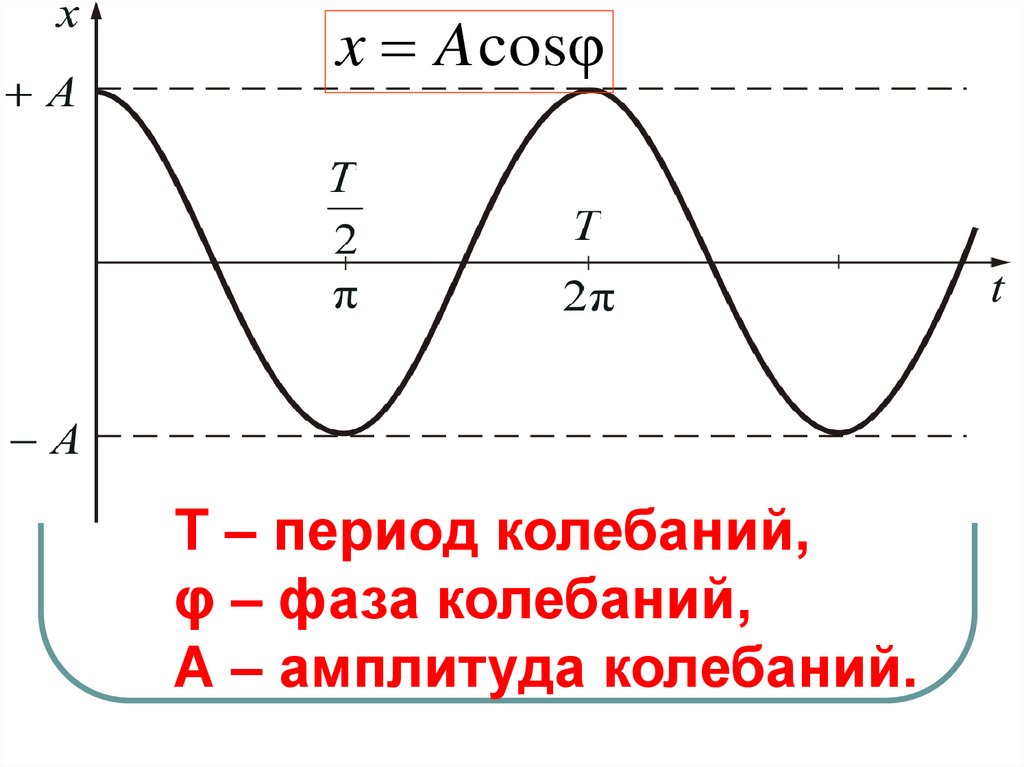
Графики смещения, скорости и ускоренияx Acos( 0t )
x m sin( 0t )
a a cos( t )
m
0
x
13.
Из графиков следует:cкорость колебаний максимальна и
равна амплитуде скорости в момент
прохождения через положение равновесия;
при максимальном смещении скорость
равна нулю;
ускорение
равно
нулю
при
прохождении телом положения равновесия
и достигает наибольшего значения, равного
амплитуде ускорения при наибольших
смещениях.
14.
Уравнение динамики гармоническихколебаний
Второй закон Ньютона в проекции на ось ОХ:
Fx ma x
2
m 0 x.
Сила пропорциональна смещению и всегда
направлена к положению равновесия. Период и
фаза силы совпадают с периодом и фазой
ускорения.
Этому условию удовлетворяют упругие силы.
Силы иной природы, удовлетворяющие этому
условию - квазиупругие.
Для квазиупругой силы Fx kx,
где k – коэффициент квазиупругой силы.
15.
km
d2 x
ax 2 ,
dt
Учитывая, что
и
получим
уравнение
динамики
ГК,
вызываемых упругими силами:
2
2
2
d x
d
x
d
x
k
m 2 kx, m
x 0
kx
0
,
2
2
m
dt
dt
dt
2
0
2
d x
2
уравнение
динамики
x
0
0
dt 2
гармонических колебаний.
Его решение
x xm sin t 0
x xm cos( 0t 0 ).
или
16.
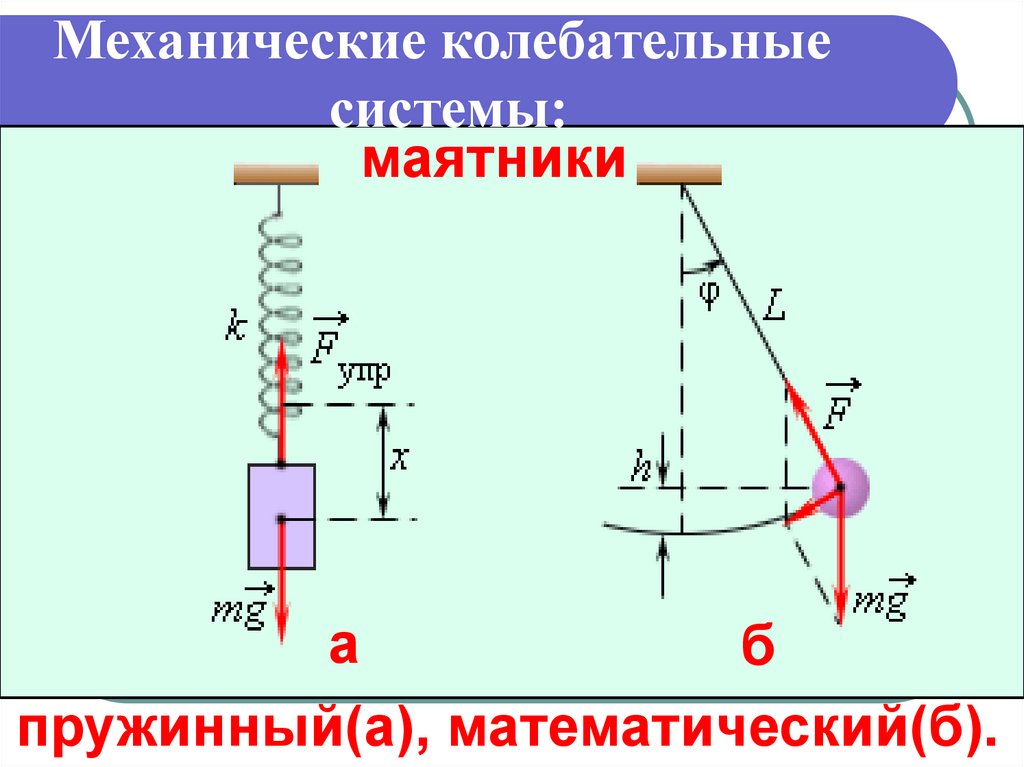
Механические колебательныеcистемы:
маятники
a
б
пружинный(а), математический(б).
17.
Гармонические осцилляторы1. Пружинный маятник –
груз массой m, подвешенный на абсолютно упругой
пружине с жесткостью k,
совершающий гармонические колебания под
действием упругой силы.
Циклическая частота и период собственных
колебаний
m
k
0
m
, T 2
k
.
18.
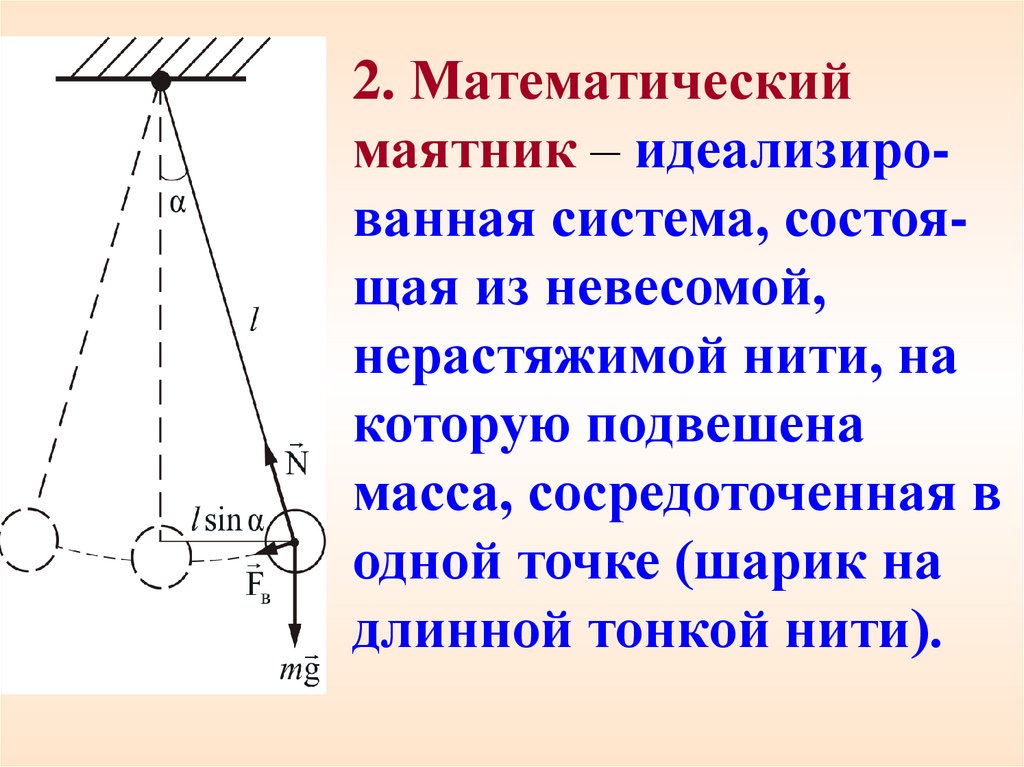
2. Математическиймаятник – идеализированная система, состоящая из невесомой,
нерастяжимой нити, на
которую подвешена
масса, сосредоточенная в
одной точке (шарик на
длинной тонкой нити).
19.
При отклонении маятника от вертикали,возникает вращающий момент
M mg sin .
Уравнение динамики вращательного
движения
M J .
Момент инерции маятника J
2
d
Угловое ускорение 2 .
d
t
g
Обозначим 02 .
Для малых углов sin .
m .
2
20.
d2
2
d
2
g
Тогдаm 2 mg sin , или
sin
0
.
2
dt
dt
Уравнение движения маятника
d
2
dt
его решение
2
0
2
0,
m cos( 0t 0 ).
Циклическая частота и период собственных колебаний математического
маятника
0
g
,
T 2
g
.
21.
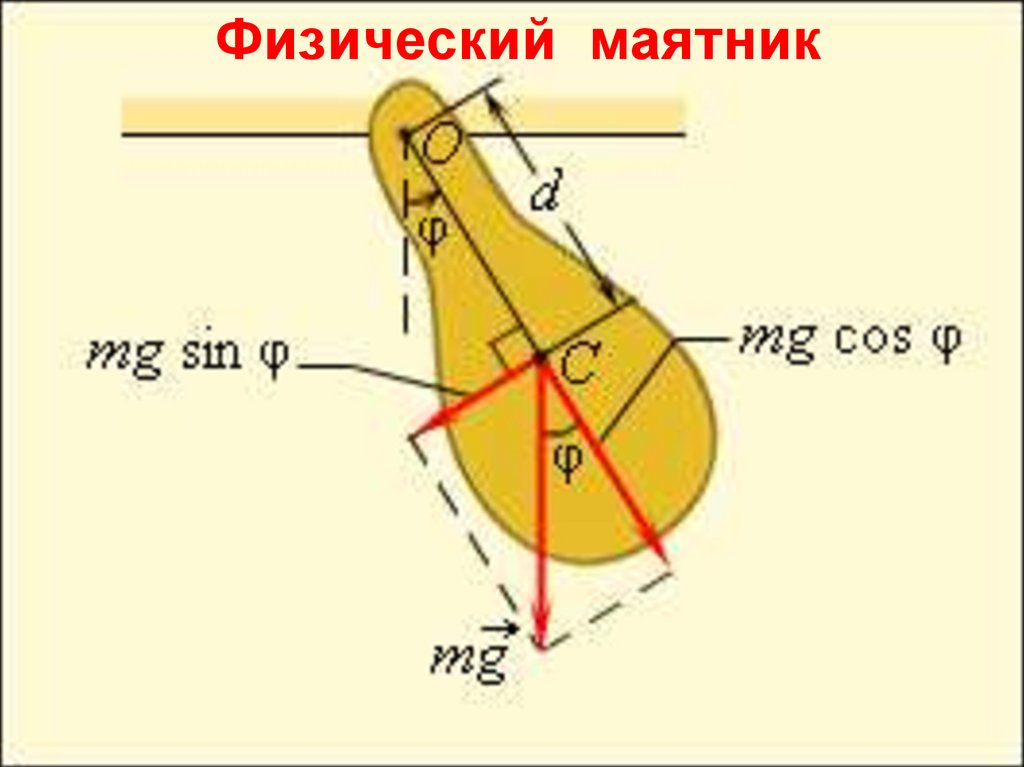
Физический маятник22.
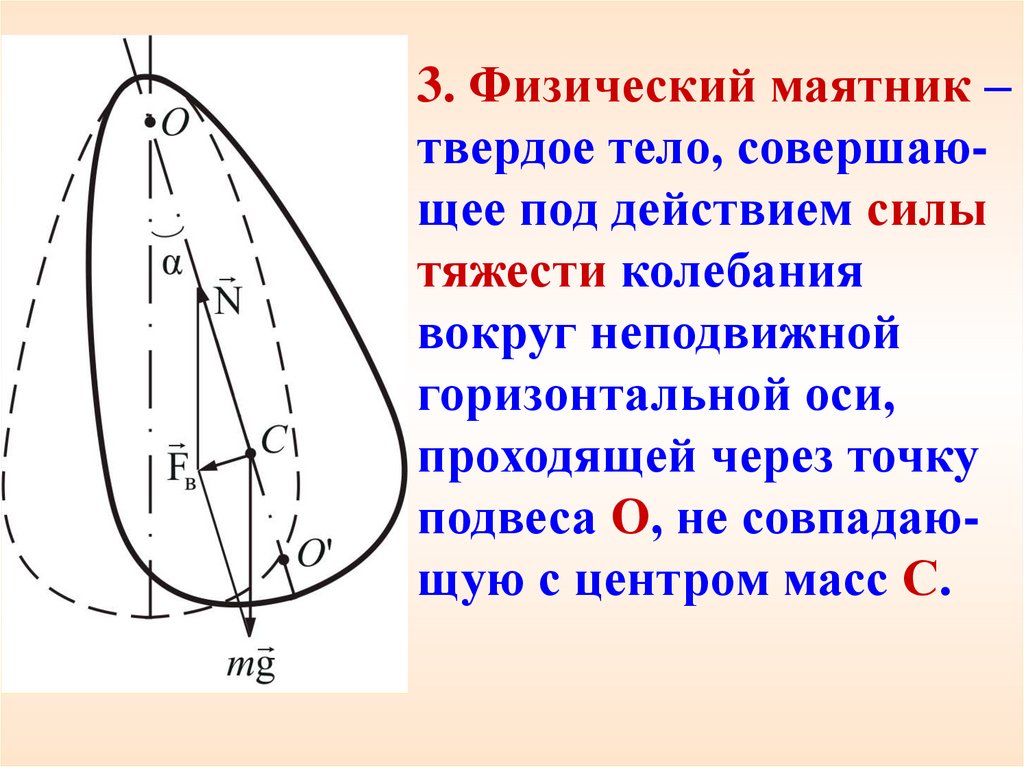
3. Физический маятник –твердое тело, совершающее под действием силы
тяжести колебания
вокруг неподвижной
горизонтальной оси,
проходящей через точку
подвеса О, не совпадающую с центром масс С.
23.
Вращающий момент силы тяжестиM mg sin ,
– расстояние между точкой подвеса и
центром инерции маятника О-С,
d
2
J
dt
2
mg sin ,
sin ,
J – момент
инерции маятника относительно точки подвеса O.
Уравнение динамики вращательного
2
движения d 2 0, его решение
dt
2
0
m cos( 0t 0 ),
24.
Циклическая частота и период собственных колебаний физического маятникаJ
mg
T 2
.
0
,
mg
J
J
Обозначим пр
- приведенная длина
m
физического маятника, тогда
T 2
пр
g
.
пр –длина математического маятника,
период колебания которого совпадает с
периодом колебаний данного физического
маятника.
25.
Соотношения для математического ифизического маятников справедливы
для малых углов отклонения (меньше
15°), когда sin мало отличается от
длины хорды x (меньше, чем на
1%).
25
26.
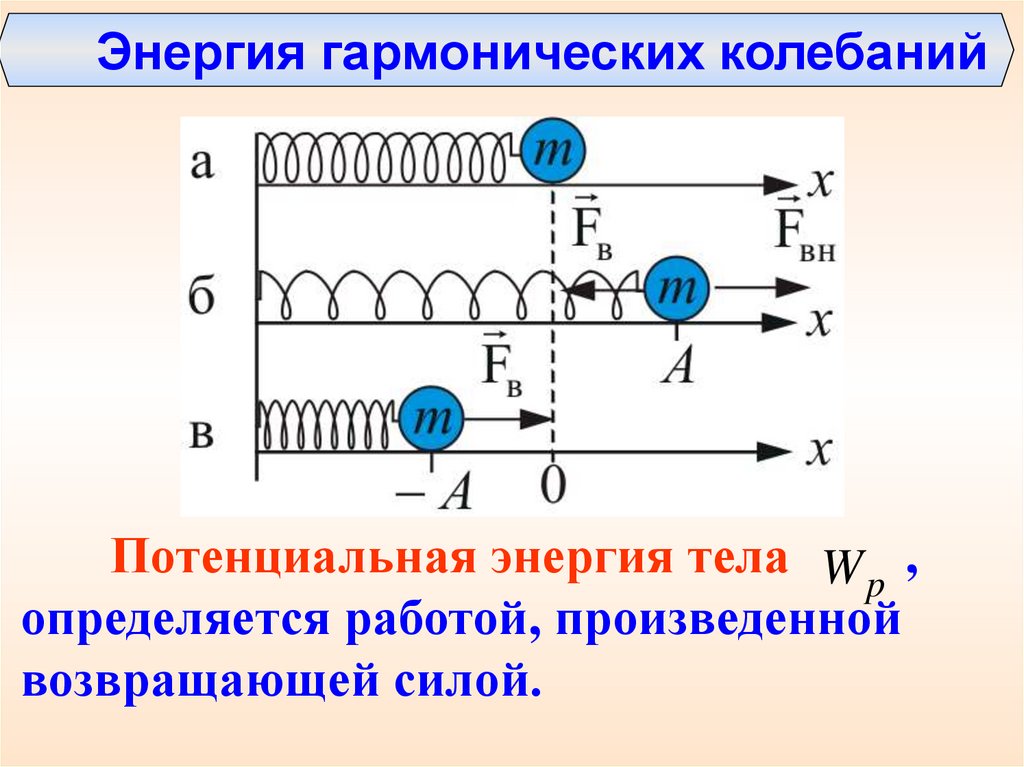
Энергия гармонических колебанийПотенциальная энергия тела W p ,
определяется работой, произведенной
возвращающей силой.
27.
FxdW p
dx
x
, dW p Fdx kxdx, W p k xdx
0
Потенциальная
2
kx
1
2
2
энергия: W p
k xm cos ( 0t 0 ).
2
2
Кинетическая
2
энергия:W m 1 m 2 x 2sin 2 ( t ).
к
0 m
0
0
2
Полная энергия:
2
1
1 2
2
2
W W p Wк m 0 xm k xm .
2
2
Полная механическая энергия тела,
совершающего ГК, пропорциональна
квадрату амплитуды.
28.
При ГК, совершающихся поддействием консервативных сил,
происходит переход кинетической
энергии в потенциальную и обратно,
но их сумма в любой момент
времени постоянна.
29.
Колебательный контурЭто
электрическая цепь, состоящая из конденсатора емкостью С
и катушки индуктивностью L.
В нем возникают электромагнитные колебания: изменяются по
гармоническому закону
Q, I , U , E , B, We , Wm .
30.
Свободные колебанияЗакон Ома для участка 1-R-L-2:
IR 1 2 c ;
dQ
Q
dI
1 2 ; c L ; I
;
C
dt
dt
2
R
Q
C
1
Q
2
I 0
dI d Q
2 ;
L dt 2 dt
d Q R dQ Q
0
2
dt
L dt LC
31.
Незатухающие свободныеколебания
R 0 d Q
2
dt
2
1
Q 0;
LC
2
2
0
d Q
dt
2
Q
0
2
0
Q Qm sin( 0t 0 );
1
2
0
; T
2
LC
.
0
LC
0
32.
Затухающие колебанияR 0
2
d Q
R dQ 1
Q
0
;
2
L dt LC
dt
2
d Q
dQ
2
2
Q
0
;
0
2
dt
dt
Q Qm e
2 T
0 ;
2
t
cos( t 0 );
2
2
0
2
2
.
33.
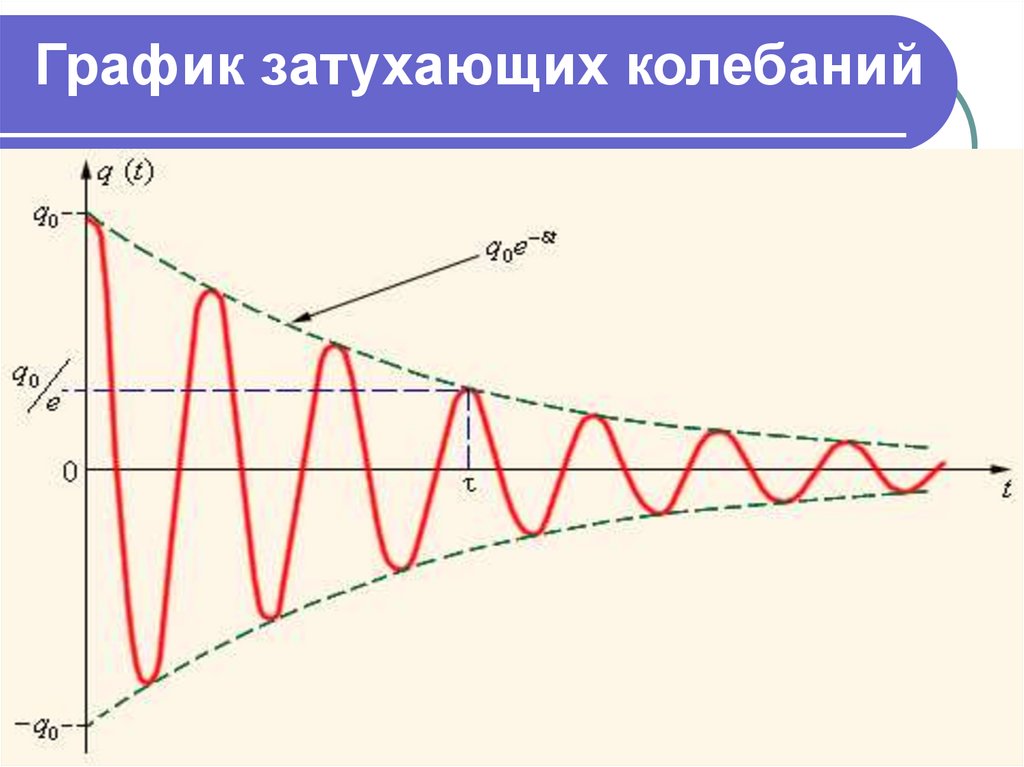
График затухающих колебаний34.
График затухающих колебанийQ
t
m
Т
;
Q
Qm t T R
- коэффициент
2 L затухания;
0
t
t
Qm e - амплитуда затухаТ
ющих колебаний;
Qm (t )
n
-логарифмический
Qm (t T ) декремент
затухания;
35.
Вынужденные колебанияДля получения незатухающих
колебаний в контур включают
источник переменной ЭДС.
Q
dI
IR L (t );
C
dt
(t ) m cos t ;
m
d Q
dQ
2
2
Q
cos
t
0
2
dt
dt
L
2
36.
Q Qm cos( t 0 )решение неоднородного уравнения,
где Qm
m
R L 1 /( C )
Q Qm cos( t 0 )
2
2
- амплитуда,
R
tg 0
- начальная фаза
L 1 /( C )
установившихся вынужденных
колебаний.
37.
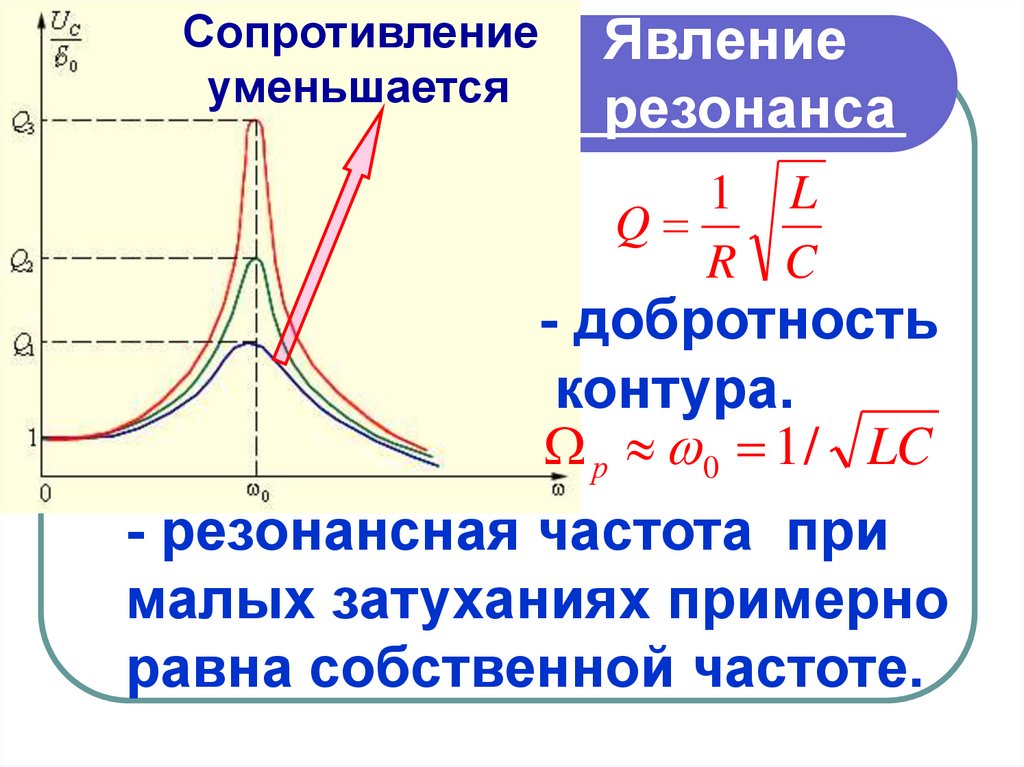
Cопротивлениеуменьшается
Явление
резонанса
1 L
Q
R C
- добротность
контура.
р 0 1 / LC
- резонансная частота при
малых затуханиях примерно
равна собственной частоте.



























 physics
physics