Матрицы и их виды. Действия над матрицами

1. Матрицы.

{
Матрицы и их виды. Действия над матрицами.

2.

Определение: Матрица – прямоугольная таблица,
образованная из элементов некоторого множества и
состоящая из m строк и n столбцов.
Обычно матрицу обозначают двойными вертикальными
черточками или круглыми скобками.
a11
a21
A
a
m1
a12
a22
...
am 2
... a1n
... a2 n
... amn
A
a11
a21
am1
a12 ... a1n
a22 ... a2 n
...
am 2 ... amn
Если m=n матрица называется квадратной.
2

3.

Среди квадратных матриц выделяют класс
диагональных матриц, т.е. матрицы, которые имеют
элементы не равные нулю только на главной
диагонали:
Если
d1 d 2 ... d n 1
то матрица называется
единичной
d1 0 ... 0
0 d 2 ... 0
D
...
0 0 ... d
n
1
0
E 0
0
0 ... 0
0 ... 0
0 1 ... 0
...
0 0 ... 1
0
1
3

4.

Матрица, у которой все элементы нулевые, получила
название нулевой:
0 0 0 ... 0
0 0 0 ... 0
0
...
0 0 0 ... 0
Понятие нулевой матрицы можно вводить и для
неквадратных матриц .
Матрицы A и B считаются равными, если они
одинакового размера, т.е. число строк и столбцов
матрицы A соответственно равны числу строк и
столбцов матрицы B и элементы стоящие на
одинаковых местах, равны между собой .
4

5.

Основные операции, которые производятся
над матрицами:
1. Сложение матриц.
2. Вычитание матриц.
3. Умножение матрицы на число.
4. Умножение матриц
5

6.

1. Суммой двух матриц А и В, одинаковых
размерностей, называется матрица той же размерности,
элементы которой равны суммам соответствующих
элементов матриц А и В:
a11
a21
A
a
m1
... a1n
b11
... a2 n
b21
B
b
... amn
m1
a11 b11 a12 b12
a21 b21 a22 b22
A B
...
a b
m1 m1 am 2 bm 2
a12
a22
...
am 2
b12 ... b1n
b22 ... b2 n
...
bm 2 ... bmn
... a1n b1n
... a2 n b2 n
... amn bmn 6

7.

Сумма матриц обладает следующими свойствами:
1. А+В=В+А, сложение матриц коммутативно,
2. А+(В+С)=(А+В)+С, свойство ассоциативности,
3. А+0=А, где 0 – нулевая матрица той же размерности.
2. Аналогично определяется разность двух матриц:
a11 b11
a21 b21
A B
a b
m1 m1
a12 b12
a22 b22
...
am 2 bm 2
... a1n b1n
... a2 n b2 n
... a mn bmn
7

8.

3. Произведением матрицы
А на число λ, называется
a11 a12
матрица, элементы которой
получаются из
A
...
соответствующих элементов
a
m1 am 2
матрицы А, путём умножения
их на число λ:
Операция произведения матрицы на число
удовлетворяет следующим свойствам:
1) 1 A A
... a1n
... amn
2) ( A) ( ) A
3) ( ) A A A 4) ( A B ) A B
5) A ( A) 0
,
Где A,B – произвольные матрицы,
-произвольные числа,
0 – нулевая матрица.8

9.

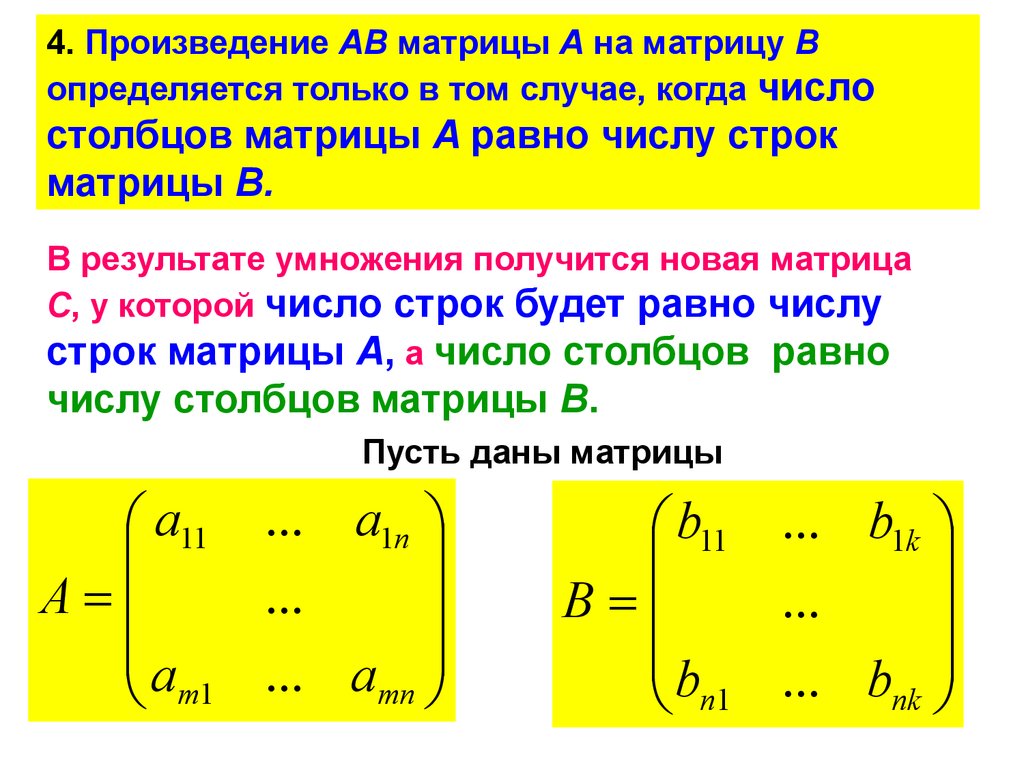
4. Произведение АВ матрицы А на матрицу В
определяется только в том случае, когда число
столбцов матрицы A равно числу строк
матрицы В.
В результате умножения получится новая матрица
C, у которой число строк будет равно числу
строк матрицы А, а число столбцов равно
числу столбцов матрицы В.
Пусть даны матрицы
a11 ... a1n
A
...
a
...
a
mn
m1
b11 ... b1k
B
...
b
...
b
nk
n1
9

10.

В таком случае произведением матрицы A на матрицу
B является матрица С
c11 ... c1k
C
...
c
...
c
mk
m1
элементы которой определяются по следующему
правилу
n
cij ai1b1 j ai 2 b2 j ... ain bnj ai b j
1
где i=1,…,m; j=1,…,k.
10

11.

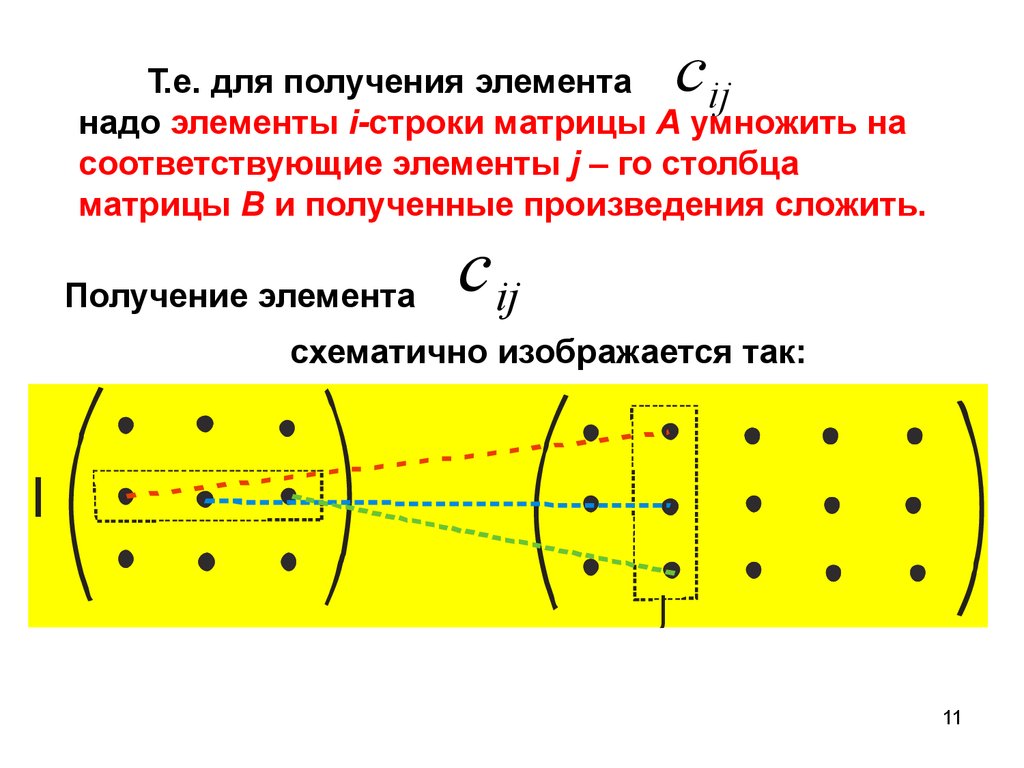
c
Т.е. для получения элемента
ij
надо элементы i-строки матрицы А умножить на
соответствующие элементы j – го столбца
матрицы B и полученные произведения сложить.
Получение элемента
cij
схематично изображается так:
I
J
11

12.

Пример:
Перемножить матрицы
1 0 2
0 1 3
3 2 1
1 5 3
2 4
и 6
5 1 7
Решение:
1 0 2 1 5 3
0 1 3 6 2 4
3 2 1 5 1 7
1 1 0 6 2 5 1 ( 5) 0 2 2 ( 1) 1 3 0 ( 4) 2 7
0 1 ( 1) 6 3 5 0 ( 5) ( 1) 2 3 ( 1) 0 3 ( 1) ( 4) 3 7
3 1 2 6 1 5
3
(
5
)
2
2
1
(
1
)
3
3
2
(
4
)
1
7
12

13.

11 7 17
9 5 25
20 12 8
Свойства умножений матриц:
1) A B B A
произведение матриц не
коммутативно;
Если AB=BA, то матрицы А и В называются
перестановочными;
13

14.

2) A ( B C ) ( A B) C
свойство ассоциативности
3) ( A B) ( A) B
4) A ( B C ) A B A C
свойство дистрибутивности
Непосредственной проверкой можно убедиться, что
A D D A (2.1)
A E E A A (2.2)
A 0 0 A 0
(2.3)
14

15.

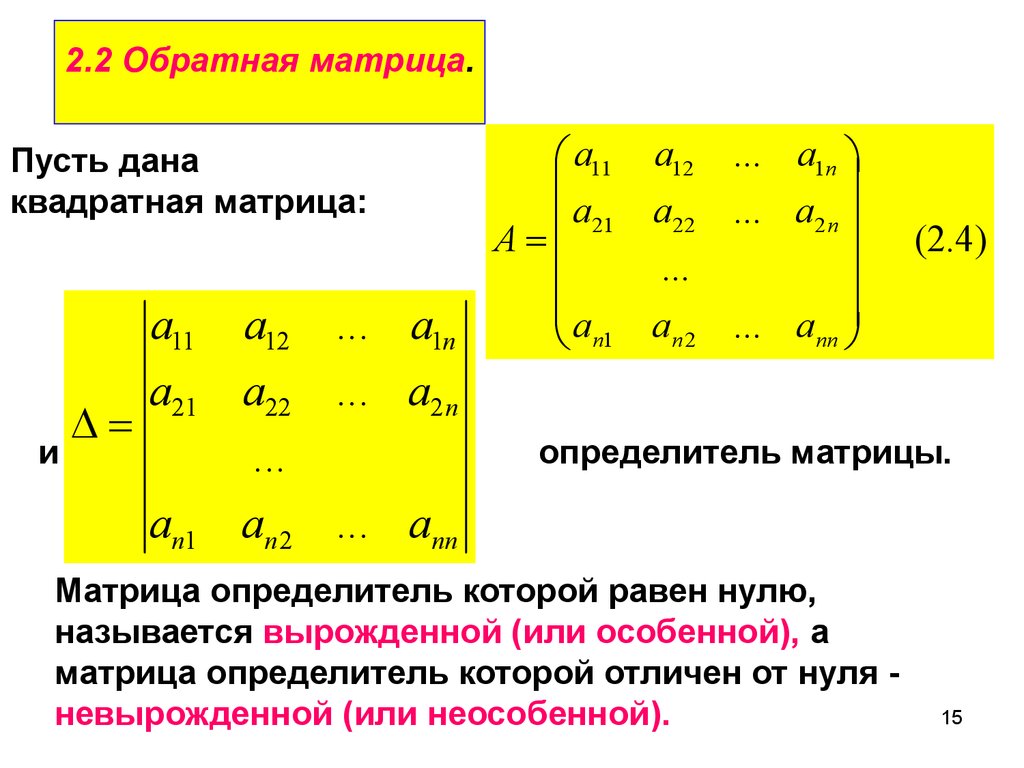
2.2 Обратная матрица.
Пусть дана
квадратная матрица:
и
a11
a21
an1
a12 ... a1n
a22 ... a2 n
...
an 2 ... ann
a11 a12 ... a1n
a21 a22 ... a2 n
A
...
a
a
...
a
n2
nn
n1
(2.4)
определитель матрицы.
Матрица определитель которой равен нулю,
называется вырожденной (или особенной), а
матрица определитель которой отличен от нуля невырожденной (или неособенной).
15

16.

Если для данной матрицы А существует матрица Х,
такая, что
(2.6)
где Е – единичная матрица, то матрица Х называется
обратной матрицей по отношению к матрице А, а
сама матрица А - обратимой.
Обратная для А матрица обозначается
1
Теорема.
Для каждой обратимой матрицы существует
только одна обратная матрица.
Доказательство.
16

17.

Пусть для матрицы А существует обратная матрица Х,
тогда должно выполняться условие (2.6)
Пусть для матрицы А существует ещё одна обратная
матрица ,
тогда согласно (2.6)
Умножим слева последнее выражение на матрицу Х:
X ( A X ) X E X
Согласно свойству произведение матриц левую часть
выражения можно записать
X ( A X ) ( X A) X EX X
Т.е. получили
Что и требовалось доказать.
17

18.

Запишем выражение для обратной матрицы
Пусть дана квадратная
обратимая матрица А:
Найдём алгебраические
дополнения для каждого
элемента и составим
матрицу В:
a11
a21
A
a
n1
A11
A12
B
A
1n
a12
a22
...
an 2
A
1
... a1n
... a2 n
... ann
A21
A22
...
A2 n
An1
... An 2
... Ann
...
Заметим, что в i строке матрицы В расположены
алгебраические дополнения элементов j столбца
определителя. Матрицу В называют присоединенной
18
для матрицы А.

19.

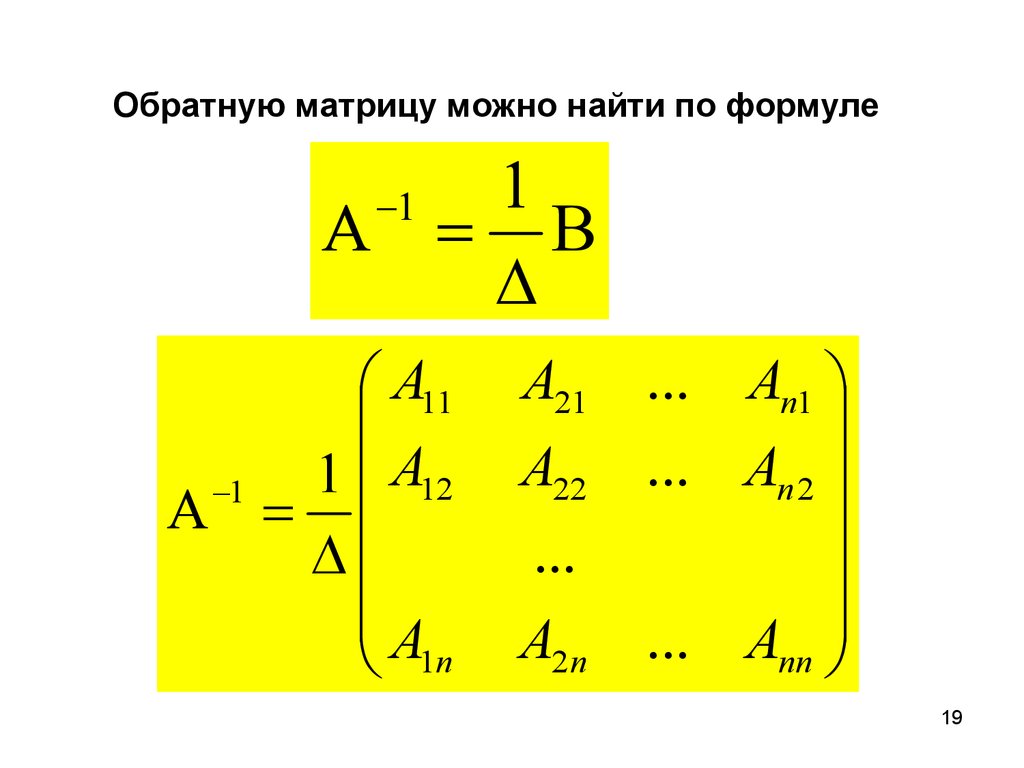
Обратную матрицу можно найти по формуле
1
1
A11
1 A12
1
A
1n
A21 ... An1
A22 ... An 2
...
A2 n ... Ann
19

20.

Пример:
Найти матрицу обратную данной
Решение:
2 3
1
3 1 1
2
1
1
Проверим, обратима матрица А или нет, т.е. является
ли она вырожденной
1
2
3
7
5
0
7 5
3 1 1 1 0 0 1( 1)
5 0
1 0
2
1 1 2 1 1
6
Найдем алгебраические дополнения всех элементов
матрицы А
20

21.

2 3
1
3 1 1
2
1
1
3
1
3 2
2 1
11 ( 1)
1 1 0 21 ( 1) 1 1 ( 2 3) 5
1 1
3
3 1
4 1
12 ( 1)
(3 2) 1 22 ( 1) 2 1 1 6 7
2 1
3
3 1
13 ( 1)
3 2 1
2
1
4
23
1 2
( 1)
(1 4) 3
2 1
5
3
2 3
5 1
10
31 ( 1)
2 3 5 32 ( 1)
3 1
1 1
21
4

22.

33 ( 1)
6
1
2
3 1
Запишем обратную
матрицу
5
5
5
0
1
1
1 7 10
5
1
3
5
Для проверки правильности решения достаточно
проверить следующее равенство:
1
A A
E
5
5 1
2 3 1 0 0
0
1
1
A A 1 7 10 3 1 1 0 1 0
5
2
0 0 1
1
3
5
1
1
22

23.

2.3 Ранг матрицы.
Рассмотрим произвольную
прямоугольную матрицу:
a11 a12
a21 a22
ak 1 a k 2
a
m1 am 2
...
...
...
...
...
...
a1k
a2 k
akk
amk
... a1m
... a2 m
... akm
... amm
Возьмем в этой матрицы k строк и k столбцов.
Элементы, стоящие на пересечении этой строки и
столбца образуют квадратную матрицу.
Определитель данной матрицы называется минором
k-ого порядка
Mk
Минор M k 1 порядка k+1, который содержит в себе
минор M
k
называется окаймляющим минором.
23

24.

Если любой минор
Mk
а все возможные миноры
не равен нулю,
M k 1
равны нулю, то говорят, что ранг матрицы равен k
(rangA=k).
Отличный от нуля минор
Mk,
называют базисным минором .
24

25.

Пример:
Вычислить ранг матрицы:
1 2 1 3
0
1 1
2
1 2 2 4
7 6 1 7
Решение:
Выберем минор второго порядка, находящийся в
верхнем левом углу,
12
12
M
1 2
2
0
4
Минор второго порядка не равен нулю, следовательно
ранг не менее двух.
Составляем миноры третьего порядка, окаймляющие
отличный от нуля минор второго порядка. Для этого
добавим к M 12 третью строку и третий столбец.
12
25

26.

123
M 123
1
2
2
0
1 3 2
1 0 0
1 2 2
124
M 123
123
M 124
1
2
5 3
1 1 ( 1)
( 6 6) 0
3 2
3 2 2
1 2 3
7 2 3
2
5 7
2
0 1 0 0 1 1 ( 1)
0
7 2
1 2 4
7 2 4
1 2 1 3 2 1
2
5 3
2 0
1 0 0
1 1 ( 1)
0
9 6
7 6 1 9 6 1
26

27.

124
M 124
1 2 3
7 2 3
2
5 7
2 0 1 0
0 1 1 ( 1)
0
21 6
7 6 7
21 6 7
Все миноры третьего порядка, окаймляющие минор
второго порядка, равны нулю. А это значит, что
rang A=2.
Другим простым способом вычисления ранга матрицы
является метод Гаусса, основанный на элементарных
преобразованиях, выполняемых над матрицей. Такими
преобразованиями являются:
1.вычёркивание строки состоящей из нулей,
2.прибавление к элементам одной из строк
соответствующих элементов другой строки, умноженных
на любое число,
3.перестановку двух строк (двух параллельных рядов),
4.все строки заменить столбцами
27

28.

Метод Гаусса вычисления ранга матрицы заключается
в том, что при помощи элементарных преобразований
матрицу можно привести к виду:
b11
0
0
0
b12
b22
0
0
... b1n
... b2 n
... b3k ... b3n
.... ...... ...
0 bkk ... bkn
...
...
b1k
b2 k
В этой матрице все диагональные элементы
и т.д. отличны от нуля, а элементы других строк
расположенные ниже, равны нулю.
b11 , b22 , b33
Т.к. ранг не меняется при элементарных
преобразованиях, то ранг исходной матрицы будет
равен рангу данной матрицы и равен числу не
нулевых строк .
28

29.

Пример:
Найти ранг матрицы:
Решение:
1
2
1
2
2
3
1
2
1
3
2
4
5
3 5
1 7
1 2
4
Добьемся, чтобы все элементы первого столбца, кроме первого
были нулями. Первую строку оставим без изменения, затем первую
строку умножим на -2 и прибавим ко второй, первую строку
умножим на -1 и прибавим к третьей, и наконец, первую строку
умножим на 2 и прибавим к четвертой строке.
1
2
1
2
2
1
2
2
3
1
3
4
4
3
1
1
5 1
5 0
7
0
2 0
2
3
3 5
0
0
6 10
4
5
5 5
3 2
7 12
29

30.

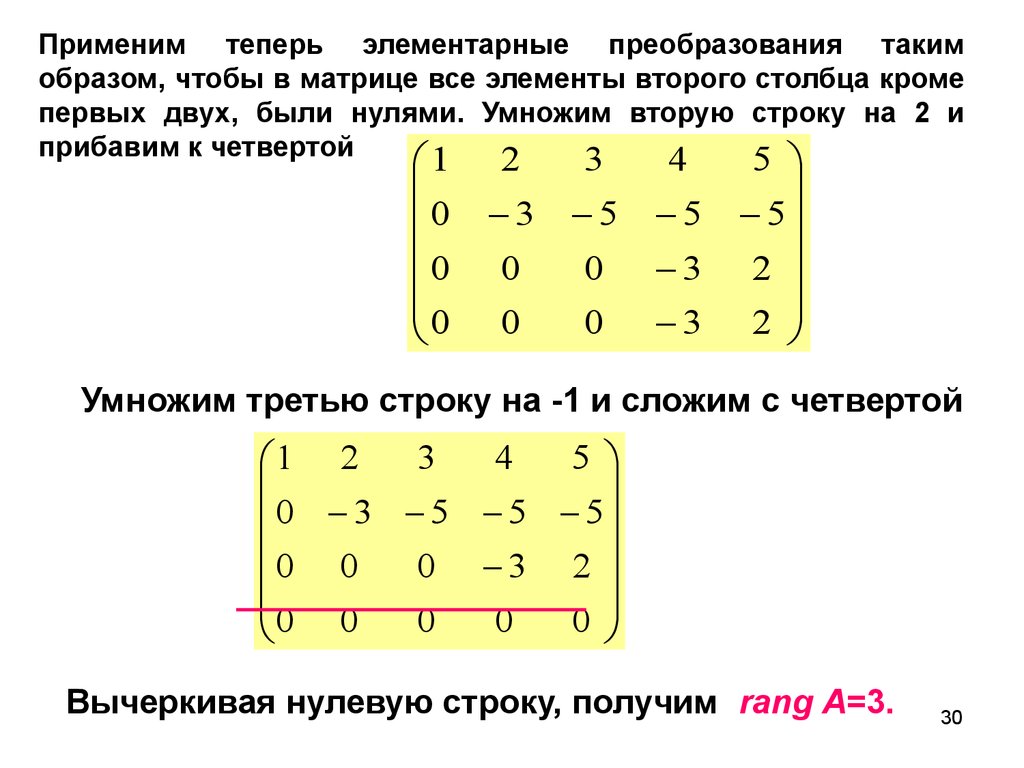
Применим теперь элементарные преобразования таким
образом, чтобы в матрице все элементы второго столбца кроме
первых двух, были нулями. Умножим вторую строку на 2 и
прибавим к четвертой
1
0
0
0
2
3
3 5
0
0
0
0
5
5
3 2
3 2
4
5
Умножим третью строку на -1 и сложим с четвертой
3
4
5
1 2
0 3 5 5 5
0 0
0 3 2
0 0
0
0
0
Вычеркивая нулевую строку, получим rang A=3.
30