Similar presentations:
Матрицы и действия над ними
1. Матрицы и действия над ними
1. Определение и некоторые виды матрицОПРЕДЕЛЕНИЕ.
Матрицей размера m n называется
таблица, образованная из элементов некоторого множества
(например, чисел или функций) и имеющая m строк и n
столбцов.
Если m n, то матрицу называют прямоугольной.
Если m n, то матрицу называют квадратной, порядка n.
Элементы, из которых составлена матрица, называются
элементами матрицы.
Например, a24 –
a13 –
2.
a11a
A 21
am1
a12
a22
am 2
a1n
a2 n ,
amn
a11 a12
a
21 a 22
A
an1 an 2
a1n
a 2n
a nn
A ( aij ) , ( i 1, m, j 1, n )
A ( aij ) , ( i, j 1, n )
Две матрицы A и B считаются равными, если они одинакового
размера, и элементы, стоящие в A и B на одинаковых
местах, равны между собой, т.е. aij bij.
3. Некоторые частные случаи матриц
a11a
1) Матрицу A 21 ( ai1 ) , размера m 1 называют
am1
матрицей-столбцом длины m
2) Матрицу A a11 a12 a1n ( a1i ) , размера 1 n
называют матрицей-строкой длиныn
3) Нулевой матрицей называют матрицу, все элементы
которой равны нулю:
0 0 0
0 0 0
O
0 0 0
4.
4) Пусть A ( aij ) , ( i 1, m, j 1, n )Элементы a11, a22, …, akk (где k min{m,n}) будем называть
элементами главной диагонали матрицы.
Квадратная матрица, у которой все элементы, стоящие вне
главной диагонали, равны нулю, называется диагональной:
a11 0 0
0 a 0
22
A
0 0 ann
Диагональная матрица, у которой все элементы главной
диагонали равны 1, называется единичной:
1 0 0
0 1 0
0 0 1
Обозначают: E или En.
5.
5) Пусть A = (aij) – квадратная матрица порядка n. Элементыa1n, a2,n-1, a3,n-2, …, an1 будем называть элементами побочной
диагонали матрицы.
Квадратные матрицы, у которых все элементы ниже (выше)
главной или побочной диагонали равны нулю, называются
треугольными :
b11 b1, n 2 b1, n 1 b1n
a11 a12 a13 a1n
0 a a a
b
b
b
0
2, n 2
2, n 1
22
23
2n
21
A 0 0 a33 a3 n , B b31 b3, n 2
0
0 ,
0 0 0 a
b 0
0
0
nn
n1
0
0
d1n
0
c11 0 0 0
0
c c
0
d
d
0
0
2, n 1
2n
21 22
C c31 c32 c33 0 , D 0 d3, n 2 d3, n 1 d3n
d d
d
d
cn1 cn2 cn3 cnn
n, n 2
n, n 1
nn
n1
6.
6) Прямоугольную матрицу размера m n будем называтьтрапециевидной, если все ее элементы ниже главной
диагонали равны нулю, т.е. если она имеет вид:
a11 a12
0 a
22
A 0 0
0 0
a13
a23
a33
0
a1m
a2 m
a3 m
amm
a1n
a2 n
a3 n
amn
7. 2. Линейные операции над матрицами
1) Умножение матрицы на число;2) Сложение матриц.
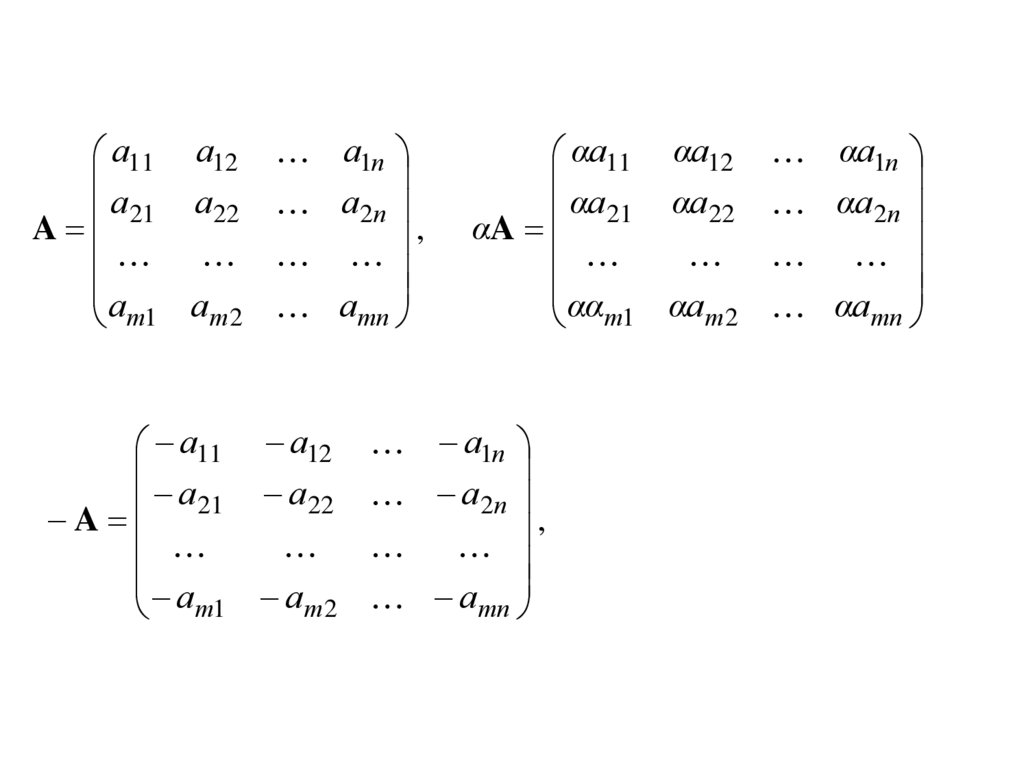
ОПРЕДЕЛЕНИЕ. Произведением матрицы A=(aij) на число
называется такая матрица B=(bij), элементы которой
равны
произведениям
соответствующих
элементов
матрицы A на число , т.е.
bij= ·aij.
Обозначают: ·A, A.
Частный случай: (-1)·A – противоположная матрице A,
Обозначают –A.
8.
a11 a12a21 a22
A
a
m1 a m2
a1n
a2 n
,
amn
a11 a12
a 21 a 22
A
a
m1 a m 2
αa11 αa12
αa 21 αa22
αA
αα
m1 αam2
a1n
a2n
,
a mn
αa1n
αa 2n
αamn
9.
10.
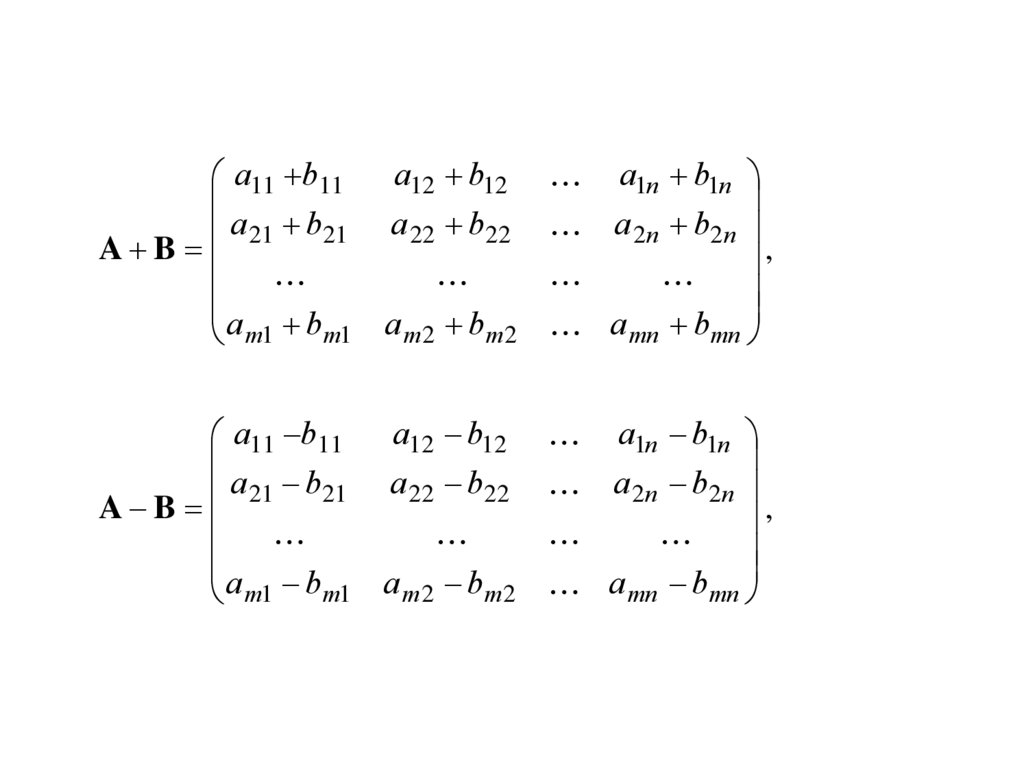
ОПРЕДЕЛЕНИЕ. Суммой двух матриц A=(aij) и B=(bij)одинакового размера, называется такая матрица C=(cij),
элементы которой равны суммам соответствующих
элементов матриц A и B, т.е. cij = aij + bij .
Обозначают: A+B
Частный случай: A+(–B) – разность матриц A и B.
Обозначают: A–B
a11 a12
a21 a22
A
a
m1 a m2
a1n
a2 n
,
amn
b11 b12
b21 b22
B
b
m1 bm 2
b1n
b2n
bmn
11.
a11 b11a 21 b21
A B
a b
m1 m1
a12 b12
a 22 b22
am2 bm2
a1n b1n
a 2n b2n
,
amn bmn
a12 b12
a11 b11
a 21 b21 a 22 b22
A B
a b
m1 m1 am 2 bm2
a1n b1n
a 2n b2n
,
a mn bmn
12.
13. Свойства линейных операции над матрицами
1) A B B A (коммутативность сложения матриц)2) ( A B ) C A ( B C ) (ассоциативность сложения
матриц)
3) A O A
4) A ( A ) O
5) ( A ) ( )A (ассоциативность относительно умножения
чисел)
6) ( )A A A (дистрибутивность умножения на
матрицу относительно сложения чисел)
7) ( A B ) A B (дистрибутивность умножения на
число относительно сложения матриц)
8) 1A A
14. 3. Нелинейные операции над матрицами
1) Умножение двух матриц;2) Транспонирование матрицы.
ОПРЕДЕЛЕНИЕ. Пусть A=(a1i) и B=(bi1) – матрица-строка и
матрица-столбец одинаковой длины n. Произведением
матрицы-строки A на матрицу-столбец B называется
матрицу
С, элемент которой число с, равное сумме
произведений их соответствующих элементов, т.е.
c a11 · b11 + a12 · b21 + a13 · b31 + … + a1n · bn1 .
15.
ОПРЕДЕЛЕНИЕ. Пусть A=(aij) – матрица размера m n,B=(bij) – матрица размера n k (т.е. количество столбцов в
матрице A совпадает с количеством строк матрицы B).
Произведением матрицы A на матрицу B называется
матрица C =(cij) размера m k такая, что каждый ее
элемент cij является произведением i-й строки матрицы
A на j-й столбец матрицы B, т.е.
cij ai1 · b1j + ai2 · b2j + ai3 · b3j + … + ain · bnj .
Обозначают: A ·B, AB.
16. Пример
Найти произведение матриц0 1 2 3
A
2 0 0 1
и
2
3
B
0
2
0 2 1 3 2 0 3 2 9
AB
2 2 0 3 0 0 1 2 6
17. Свойства операции умножения матриц
1) AE EA A , AO OA O2) ( AB )C A( BC ) (ассоциативность умножения матриц)
3) ( A B)C AC BC
дистрибутивность умножения
4) C( A B) CA CB
матриц относительно сложения матриц.
18.
ОПРЕДЕЛЕНИЕ. Пусть A – матрица размера m n.Матрица размера n m, полученная из A заменой каждой
ее строки столбцом с тем же номером, называется
транспонированной к A и обозначается AТ.
Операция нахождения матрицы AТ называется
транспонированием матрицы A.
a11 a12
a21 a22
A
a
m1 a m2
a1n
a2 n
,
amn
a11
a12
T
A
α
1n
a21 am1
a22 a m 2
a2n amn
19. ТРАНСПОНИРОВАНИЕ МАТРИЦЫ
412
Исходная
A 17
29
матрица (размер 3 на 2)
30 36
12 17 30 Транспонированная
A
матрица (размер 2 на 3)
4
29
36
T
20.
Свойства операции транспонирования матриц1) (AТ )T = A ;
2) (A + B)T = AT + BT ;
3) (αA)T = αAT ;
4) (A · B)T = BT · AT .







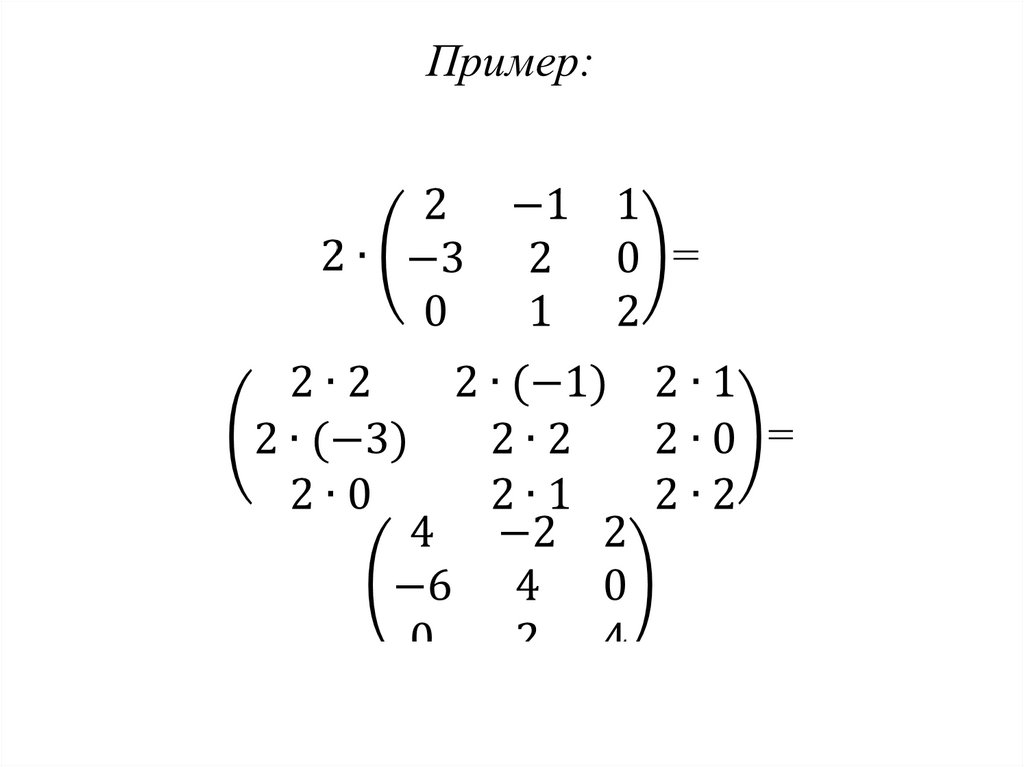

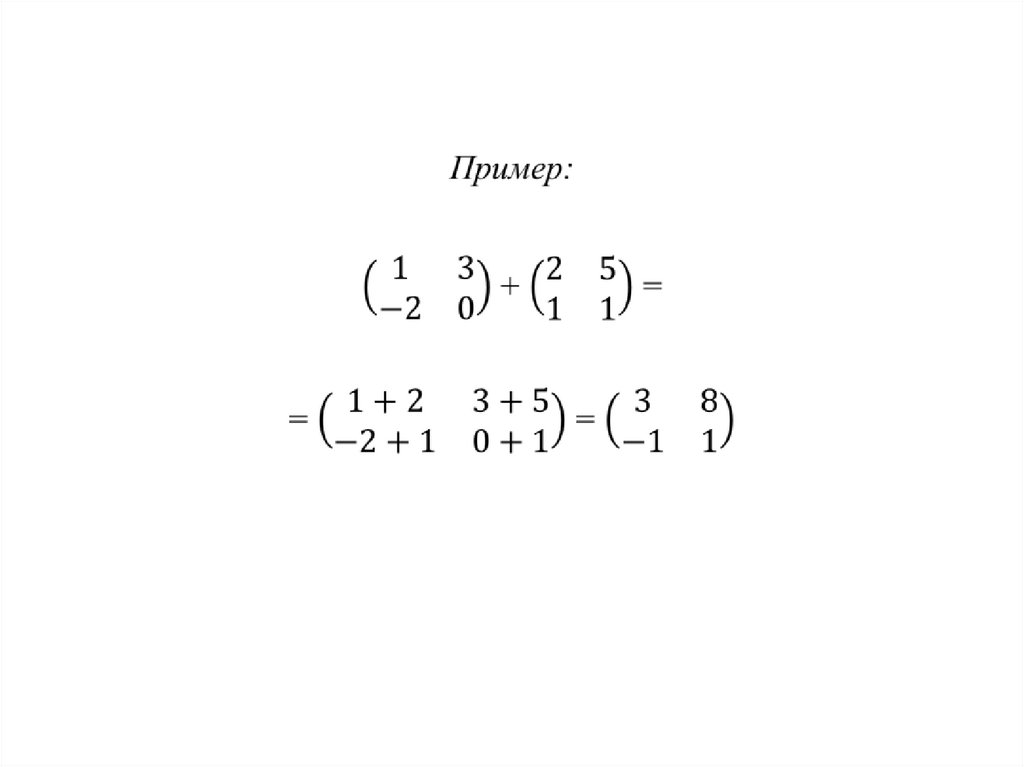








 mathematics
mathematics








