Матрицы и действия над ними

1. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ

2.

Матрица:
a11 a12
a
a22
21
A
...
...
am1 am 2
a1n
... a2 n
... ...
... amn
...
Размерность матрицы: Am n
m количество строк ,
n количество столбцов
Элемент матрицы:
aij
i номер строки,
j номер столбца

3.

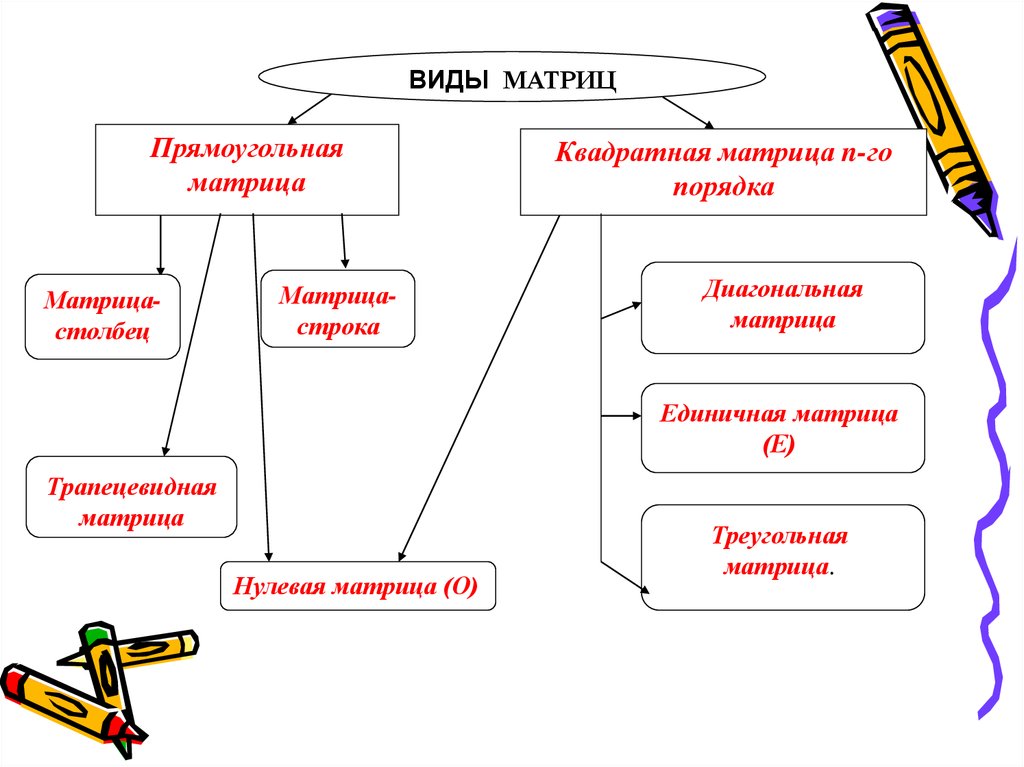
ВИДЫ МАТРИЦ
Прямоугольная
матрица
Матрицастолбец
Матрицастрока
Квадратная матрица n-го
порядка
Диагональная
матрица
Единичная матрица
(Е)
Трапецевидная
матрица
Нулевая матрица (О)
Треугольная
матрица.

4.

5.

6.

ДЕЙСТВИЯ НАД МАТРИЦАМИ:
умножение матрицы на
действительное число;
сложение и вычитание матриц;
умножение матрицы на матрицу;
возведение матрицы в степень;
транспонирование.

7. Умножение матрицы на действительное число

∙А = А ∙ = С
где А – матрица произвольной размерности
И
cij aij
(i 1, m, j 1, n)

8. Сложение (вычитание) матриц

А+В=С
(А – В = С),
где А, В – матрицы одинаковой размерности
и
cij aij bij (i 1, 2,..., m; j 1, 2,...n)

9.

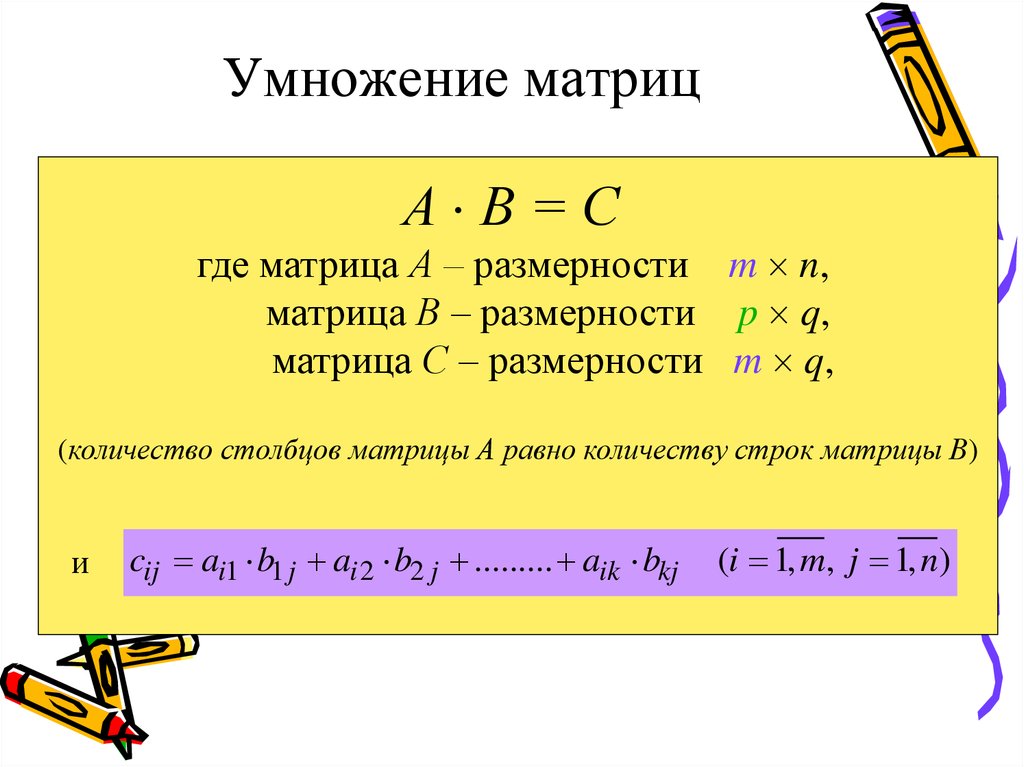
10. Умножение матриц

А В=С
где матрица А – размерности m n,
матрица В – размерности p q,
матрица С – размерности m q,
(количество столбцов матрицы А равно количеству строк матрицы В)
и
cij ai1 b1 j ai 2 b2 j ......... aik bkj
(i 1, m, j 1, n)

11.

12. Формула и схема вычисления элемента c11 в случае :

Формула и схема вычисления
элемента c11 в случае А2 3 В3 3 = С2 3:
c11 a11 b11 a12 b21 a13 b31
1 2 1
A
3
1
2
1 0 1
B 2 1 3
1 2 1

13.

14. Возведение матриц в степень

А A A = Ak ,
где А – квадратная матрица,
в частности
А A =A2,
А A A = A3

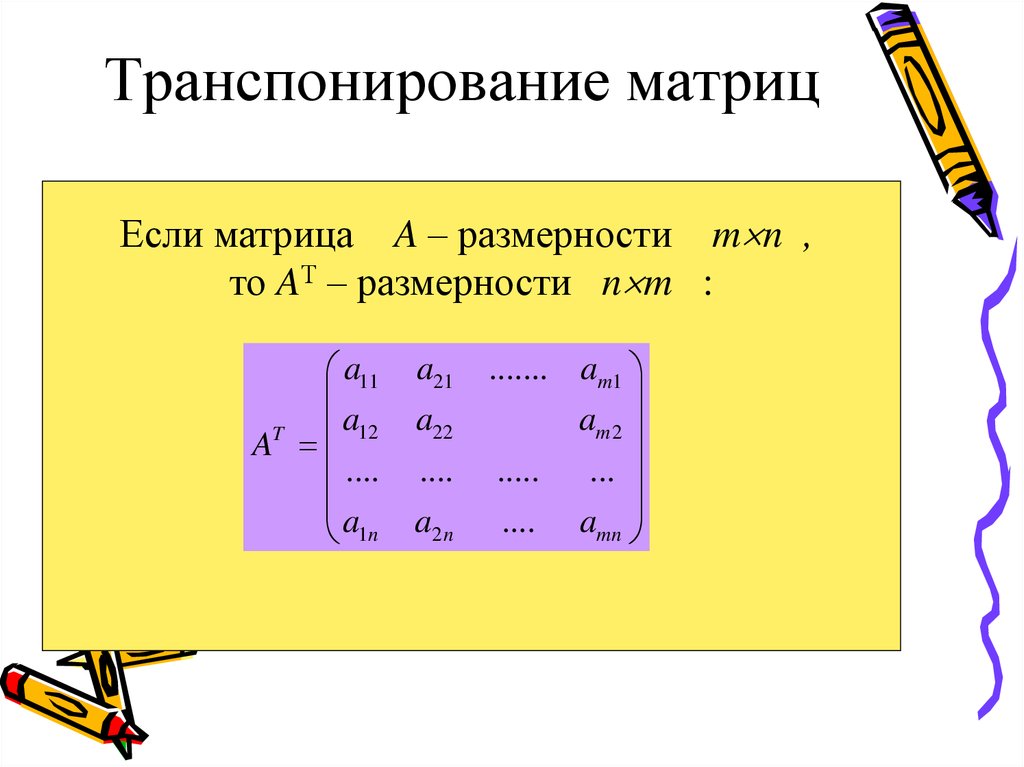
15. Транспонирование матриц

Если матрица A – размерности m n ,
то AТ – размерности n m :
a11
a12
T
A
....
a1n
a21
a22
....
a2 n
....... am1
am 2
..... ...
.... amn

16. Спасибо за внимание!!! =)