Similar presentations:
Свойства определенных интегралов. Лекция №8
1. Здравствуйте!
Лекция №82.
Свойства определенных интегралов1. Интеграл по ориентированному промежутку.
b
Когда вводилось понятие определенного интеграла
f ( x)dx , то
a
неявно предполагалось, что нижний предел меньше верхнего, то
a
есть что a b . А можно ли придать смысл интегралу
f ( x)dx ?
b
Такой смысл придается
промежутка интегрирования.
a = x0
x1
x2
введением понятия
x3
...
xn-1
ориентации
b = xn
3.
Вспомним еще раз, как строилось понятие определенногоинтеграла. Отрезок [a, b] разбивался на кусочки, по которым
строилась интегральная сумма. Представим теперь, что эти кусочки
проходятся в направлении от точки а к точке b и величина xi
определяется так: из координаты точки, которая проходится позже
вычитается координата точки, которая проходится раньше то есть
xi xi 1 xi .
a
А теперь вернемся к интегралу
f ( x)dx .
Что изменилось?
b
Нижний предел стал b, а верхний а. Это трактуют так: отрезок
[a, b] проходится теперь в обратном направлении, от точки b к
точке а:
a = x0
x1
x2
x3
...
xn-1
b = xn
4.
Но тогда меняются величины xi : они становятся равнымиxi xi xi 1, так как теперь точка xi проходится позже точки xi 1.
Очевидно соотношение между этими величинами: xi xi .
Но тогда интегральные суммы в первом и втором случаях
принимают вид
n 1
f ( i ) xi ;
i 0
n 1
f ( i ) xi ,
i 0
и, после предельного перехода 0 , получаем соотношение
b
a
a
b
f ( x)dx f ( x)dx .
a
Следствие. Рассмотрим интеграл
f ( x)dx , у которого верхний
a
и нижний пределы одинаковы. Меняя их местами, получим
a
a
a
a
a
a
f ( x)dx f ( x)dx , откуда следует, что f ( x)dx 0 .
5.
2. Если a c b , тоb
c
b
a
a
c
f ( x)dx f ( x)dx f ( x)dx .
Это свойство называется аддитивностью определенного интеграла
относительно промежутка интегрирования.
b
c
a
Снова рассмотрим разбиение промежутка [a, b] на кусочки так,
что точка с попадает в число точек деления. Тогда относительно
интегральных сумм можно написать
f ( i ) xi f ( i ) xi f ( i ) xi .
i:xi [ a , b )
i:xi [ a , c )
i:xi [ c , b )
6.
Делая предельный переход 0 , получаемlim f ( i ) xi lim f ( i ) xi lim
0
0
i:xi [ a , b )
0
i:xi [ a , c )
f ( ) x ,
i:xi [ c , b )
что и приводит к требуемому соотношению:
b
c
b
a
a
c
f ( x)dx f ( x)dx f ( x)dx .
i
i
7.
bb
a
a
3. kf ( x)dx k f ( x)dx .
Действительно, для интегральных сумм верно соотношение
n 1
kf ( ) x
i 0
i
i
n 1
k f ( i ) xi .
После предельного перехода 0
i 0
n 1
n 1
lim kf ( i ) xi k lim f ( i ) xi
0
0
i 0
b
b
a
a
получаем, что kf ( x)dx k f ( x)dx .
i 0
8.
bb
b
a
a
a
4. [ f ( x) g ( x)]dx f ( x)dx g ( x)dx .
Записывая соотношение для интегральных сумм
n 1
n 1
n 1
[ f ( ) g ( )] x f ( ) x g ( ) x
i
i 0
i
i
i 0
и делая предельный переход 0
n 1
i
i
i 0
n 1
i
n 1
i
lim [ f ( i ) g ( i )] xi lim f ( i ) xi lim g ( i ) xi ,
0
0
i 0
0
i 0
i 0
получим требуемое соотношение
b
b
b
a
a
a
[ f ( x) g ( x)]dx f ( x)dx g ( x)dx .
9.
5. Если a b , тоb
b
a
a
f ( x)dx | f ( x) | dx .
Действительно, так как a b , то все xi 0 . Поэтому
n 1
n 1
f ( ) x | f ( ) | x .
i 0
i
i
i 0
i
i
Делая предельный переход 0 и учитывая непрерывность
функции | x | , получим
n 1
n 1
n 1
lim f ( i ) xi lim f ( i ) xi lim | f ( i ) | xi ,
0
что и дает
0
i 0
b
b
a
a
i 0
f ( x)dx | f ( x) | dx .
0
i 0
10.
6. Если a b и x [a, b] f ( x) g ( x) , тоb
b
a
a
f ( x)dx g ( x)dx .
Действительно, в этом случае i f ( i ) g ( i ) , и, так как все
xi 0 , то i f ( i ) xi g ( i ) xi . Суммируя
n 1
n 1
f ( ) x g ( ) x
i 0
i
i
и переходя к пределу 0
i
i 0
n 1
i
n 1
lim f ( i ) xi lim g ( i ) xi ,
0
0
i 0
получим требуемое свойство
b
i 0
b
a
a
f ( x)dx g ( x)dx
11.
Первая теорема о среднемТеорема. Пусть
1. функции f (x) и g (x ) интегрируемы на [a, b] ;
2. существуют
конечные
m
и
M
x [a, b] m f ( x) M ;
3. x [a, b] g ( x) 0 .
Тогда существует число такое, что
1. m M ;
2.
b
b
a
a
f ( x) g ( x)dx g ( x)dx .
такие,
что
12.
Доказательство.Имеем x [a, b] m f ( x) M . Так как x [a, b] g ( x) 0 , то
x [a, b] mg( x) f ( x) g ( x) Mg ( x) .
Интегрируя это неравенство, получаем
b
b
b
m g ( x)dx f ( x) g ( x)dx M g ( x)dx .
a
a
(*)
a
Возможны следующие варианты:
b
а)
g ( x)dx 0 .
b
Но тогда из (*) следует, что
a
может быть взято любым.
f ( x) g ( x)dx 0
a
и
13.
б)b
b
a
a
g ( x)dx 0 . Тогда, деля все части неравенства (*) на g ( x)dx ,
получим:
b
m f ( x) g ( x)dx
a
Обозначим
g ( x)dx M .
a
b
b
a
a
f ( x) g ( x)dx g ( x)dx . Тогда будет
1. m M ;
2.
b
b
b
a
a
f ( x) g ( x)dx g ( x)dx .
14.
Следствие. Если f (x) непрерывна на [a, b] , то c [a, b] такая,что
b
b
a
a
f ( x) g ( x)dx f (c) g ( x)dx .
Доказательство. Имеем следующую цепочку следствий:
f (x) непрерывна на [a, b] по первой теореме Вейерштрасса
существуют m inf f ( x) и M sup f ( x) так что
x [ a , b ]
x [ a , b ]
x [a, b] m f ( x) M по второй теореме Больцано Коши
c [a, b] такая, что для [m, M ] f (c) . Заменяя в первой
теореме о среднем на f (c ) , получим следствие.
15.
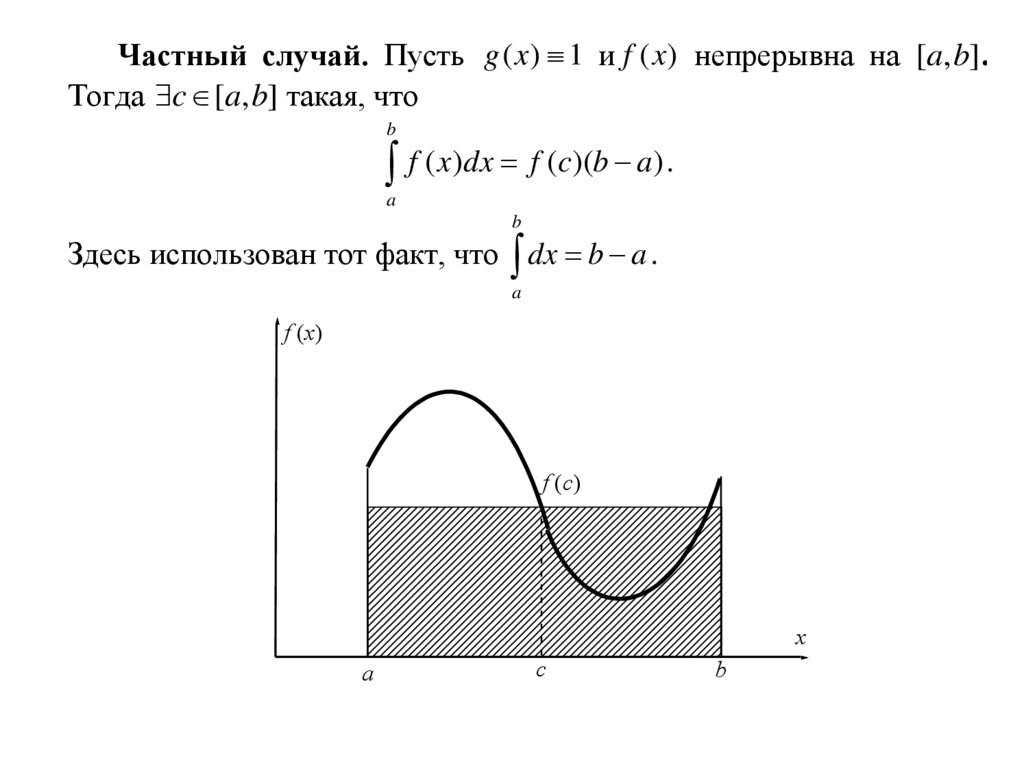
Частный случай. Пусть g ( x) 1 и f (x) непрерывна на [a, b] .Тогда c [a, b] такая, что
b
f ( x)dx f (c)(b a) .
a
b
Здесь использован тот факт, что dx b a .
a
f (x)
f (c)
x
a
c
b
16.
Вычисление определенных интеграловФормула Ньютона Лейбница
Теорема 1. Если существует непрерывная функция F (x )
такая, что x [a, b] F ( x) f ( x) , то
b
f ( x)dx F ( x) a F (b) F (a ) .
b
a
b
(обратите внимание на символику: символ F ( x) a означает разность
F (b) F (a) ).
Эта формула носит название формулы Ньютона Лейбница.
17.
ДоказательствоКак и при построении понятия определенного интеграла,
разобьем отрезок [a, b] произвольным образом на части (кусочки)
точками a x0 x1 x2 x3 ... xn 1 xn b .
a = x0
x1
x2
x3
...
xn-1
b = xn
18.
Тогда имеемF (b) F (a) F ( xn ) F ( x0 )
F ( xn ) F ( xn 1 ) F ( xn 1 ) F ( xn 2 ) ... F ( x1 ) F ( x0 )
n 1
n 1
i 0
i 0
F ( xi 1 ) F ( xi ) f ( i ) xi .
После предельного перехода 0 , получим
b
F (b) F (a ) lim f ( x)dx .
0
Непрерывность F (x ) обязательна!
a
19.
Обобщенная формула Ньютона ЛейбницаТеорема 2. Пусть равенство F ( x) f ( x) верно всюду, за
исключением конечного числа точек x1 , x2 , ... , xk . Тогда
b
k
f ( x)dx F (b) F (a) F ( x 0) F ( x 0) .
a
Эта
формула
носит
Ньютона Лейбница.
i 1
название
i
i
обобщенной
формулы
20.
Доказательство.Имеем
b
x1
x1
a
a
x1
f ( x)dx f ( x)dx f ( x)dx
x2
x2
x1
x2
b
f ( x)dx f ( x)dx ... f ( x)dx .
xk
Но, по первой теореме о среднем,
xi
0 .
f ( x)dx ( x ) ( x ) 2
i
xi
i
0
21.
Поэтомуx
b
x
f ( x)dx f ( x)dx ... f ( x)dx
a f ( x)dx lim
0
a
x
x
lim F ( x1 ) F (a) F ( x2 ) F ( x1 ) ... F (b) F ( xk )
b
1
2
1
0
k
F ( x1 0) F (a) F ( x2 0) F ( x1 0) ... F (b) F ( xk 0)
k
F (b) F (a ) F ( xi 0) F ( xi 0) .
i 1
22.
Интегрирование определенных интегралов по частямВспомним формулу интегрирования неопределенных интегралов
по частям
udv uv vdu .
Переходя к определенным интегралам, получим:
b
udv udv
a
b
a
b
uv a vdu
b
a
b
u (b)v(b) u ( a )v( a ) vdu .
a
Итак
b
b
a
a
udv u (b)v(b) u (a)v(a) vdu .
Эта
формула носит
название
определенных интегралов по частям.
формулы
интегрирования



















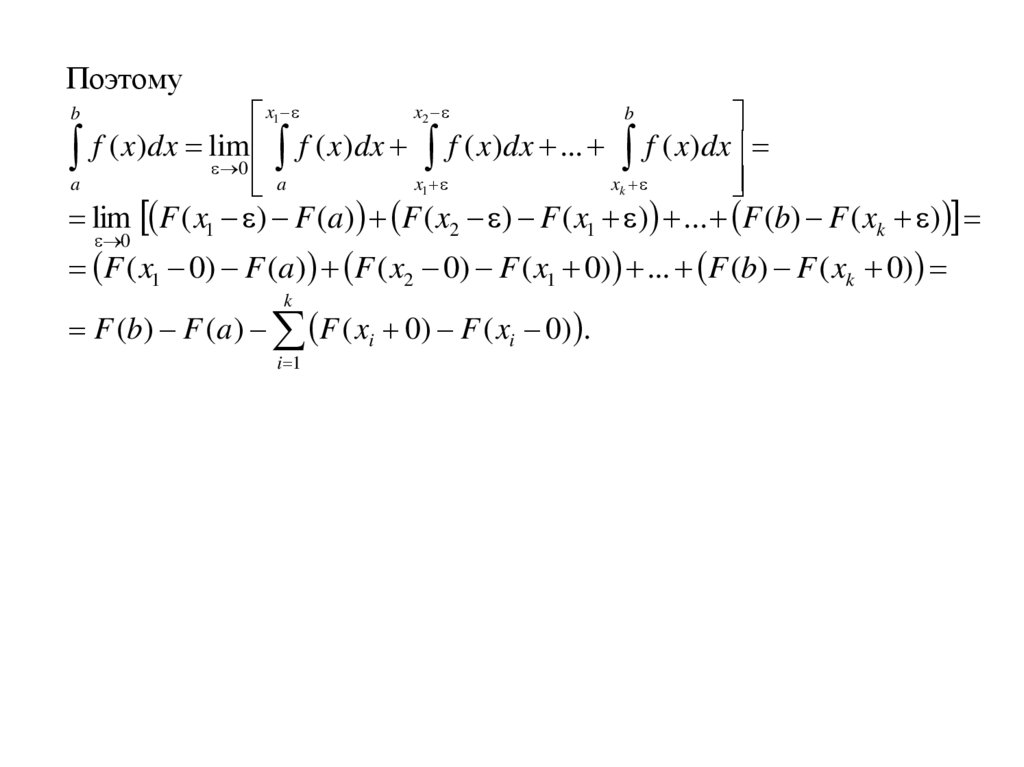

 mathematics
mathematics