Двугранный угол. Перпендикулярность плоскостей

1.

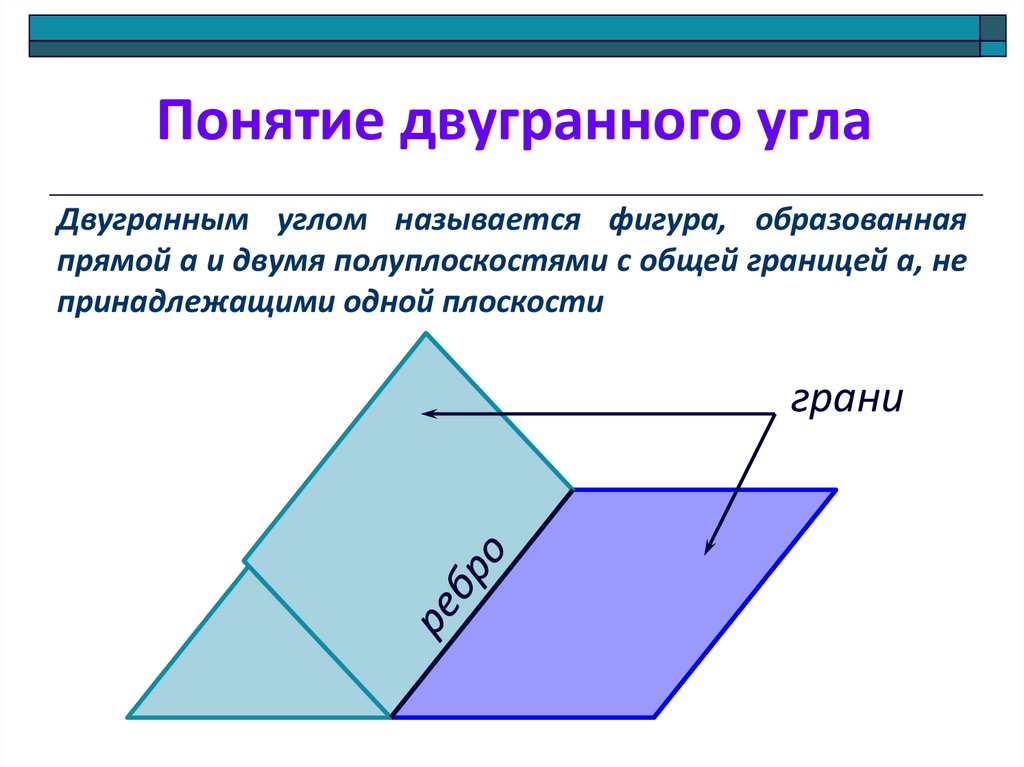
2. Понятие двугранного угла

Двугранным углом называется фигура, образованная
прямой а и двумя полуплоскостями с общей границей а, не
принадлежащими одной плоскости
грани

3. Применение двугранных углов

4.

Применение двугранных углов

5.

Применение двугранных углов

6.

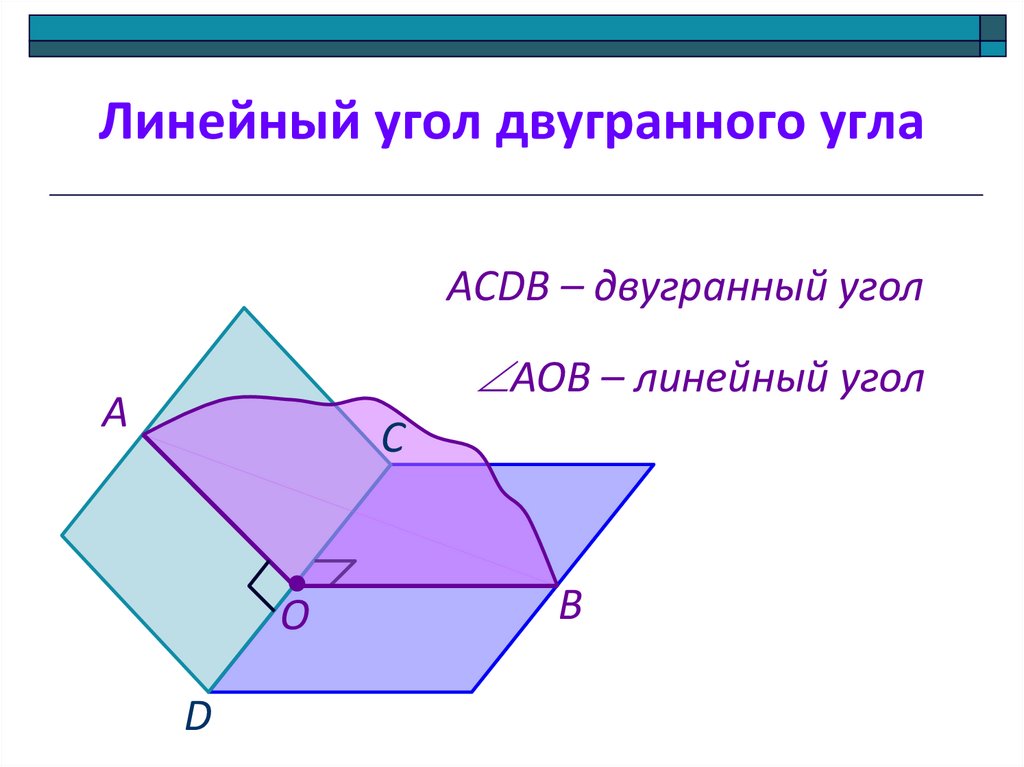
7. Линейный угол двугранного угла

АCDB – двугранный угол
АОB – линейный угол
А
С
О
D
В

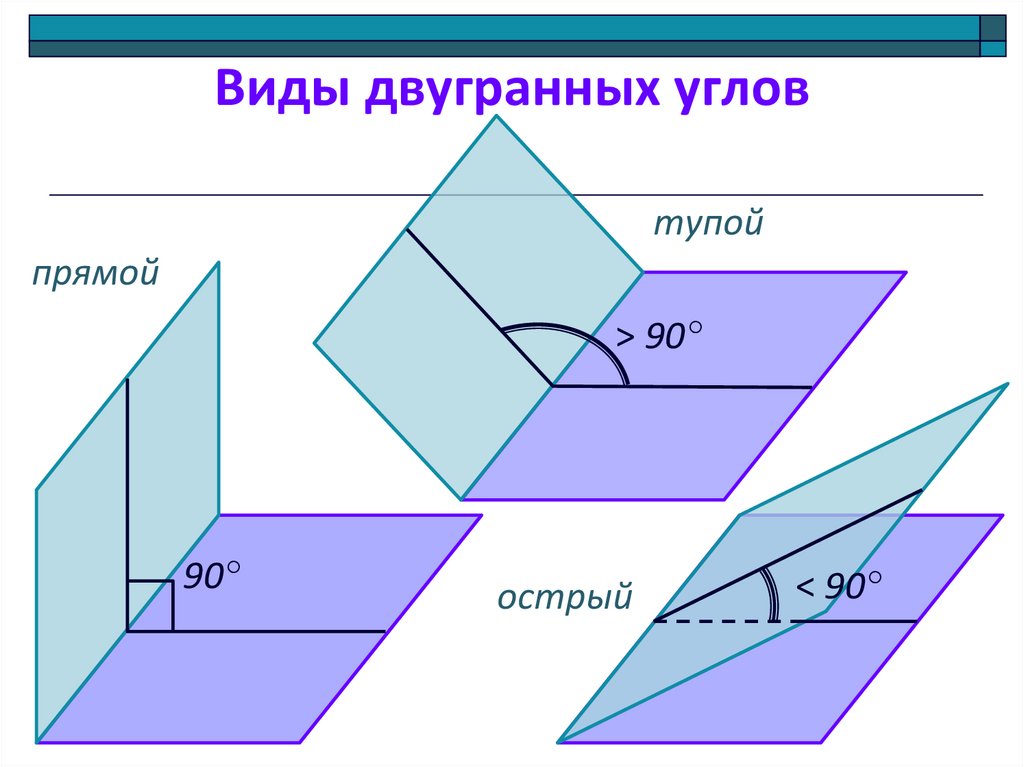
8. Виды двугранных углов

тупой
прямой
> 90°
90°
острый
< 90°

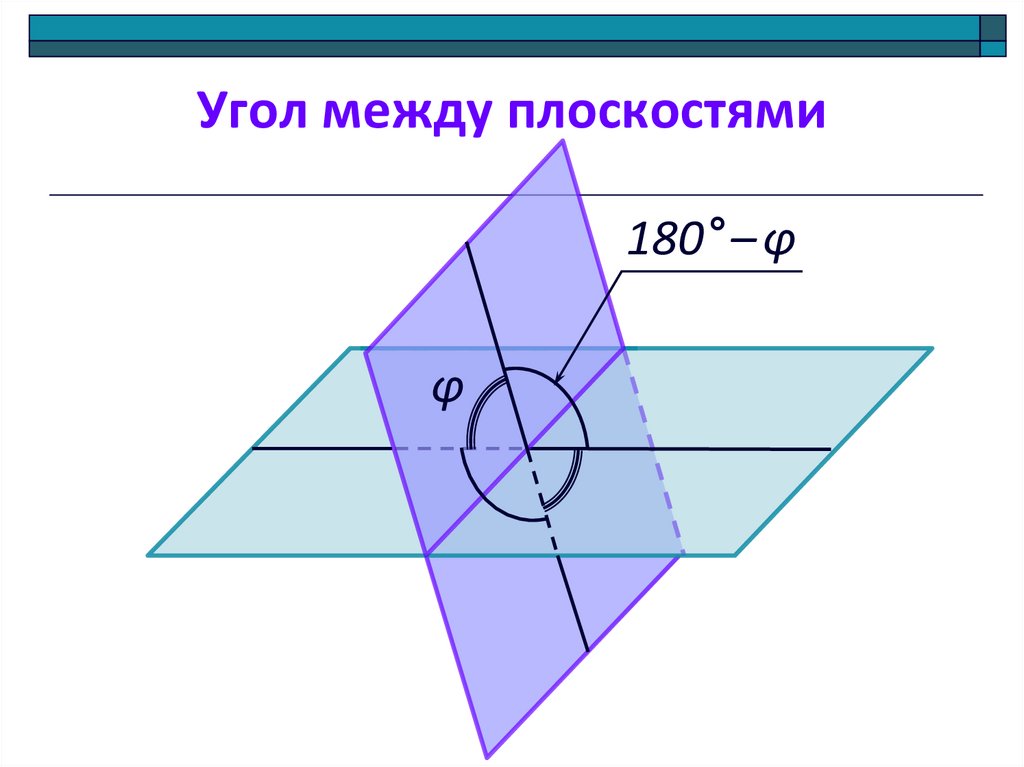
9. Угол между плоскостями

180° – φ
φ

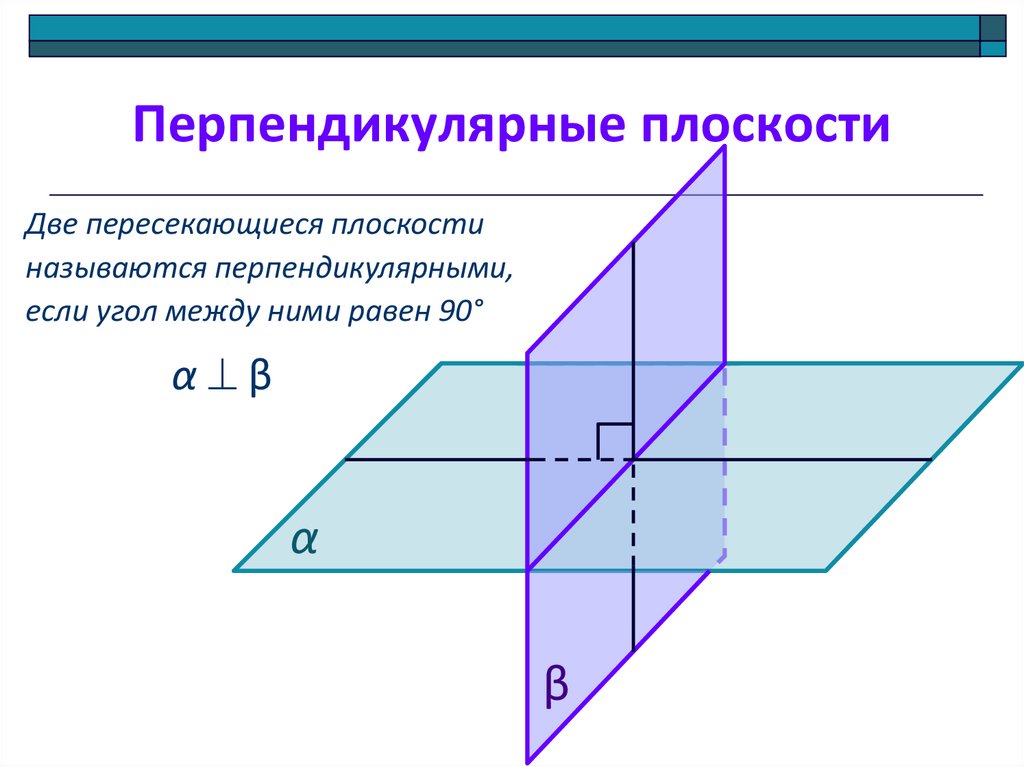
10. Перпендикулярные плоскости

Две пересекающиеся плоскости
называются перпендикулярными,
если угол между ними равен 90°
α β
α
β

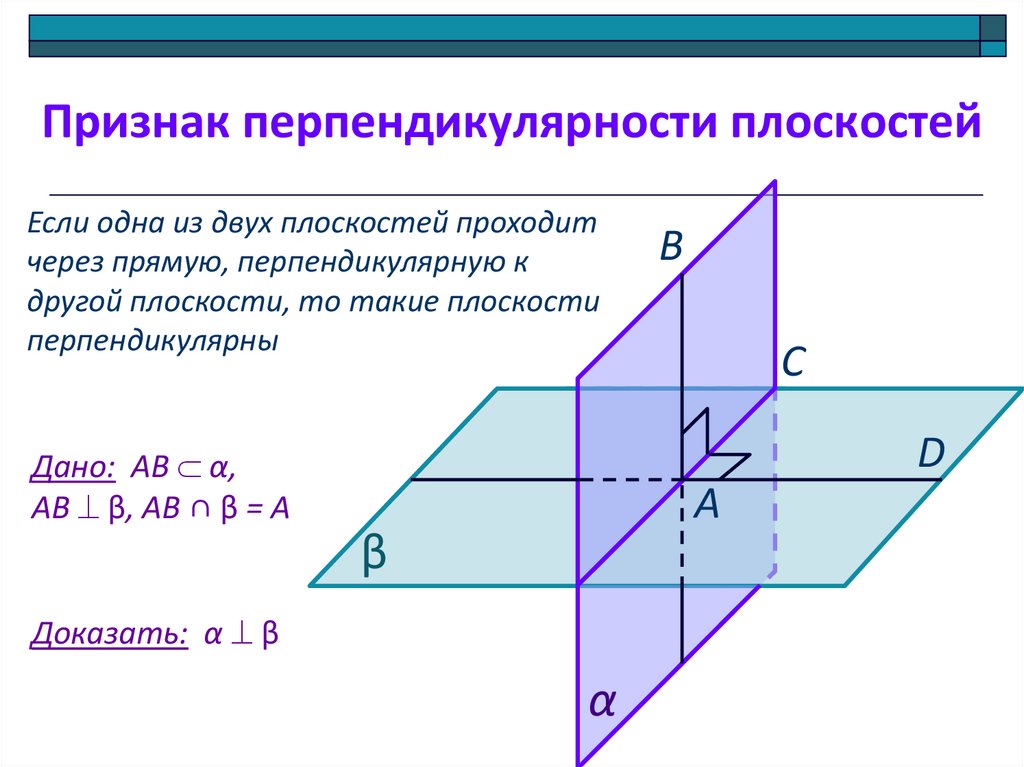
11. Признак перпендикулярности плоскостей

Если одна из двух плоскостей проходит
через прямую, перпендикулярную к
другой плоскости, то такие плоскости
перпендикулярны
В
С
D
Дано: АВ α,
АВ β, АВ ∩ β = А
А
β
Доказать: α β
α

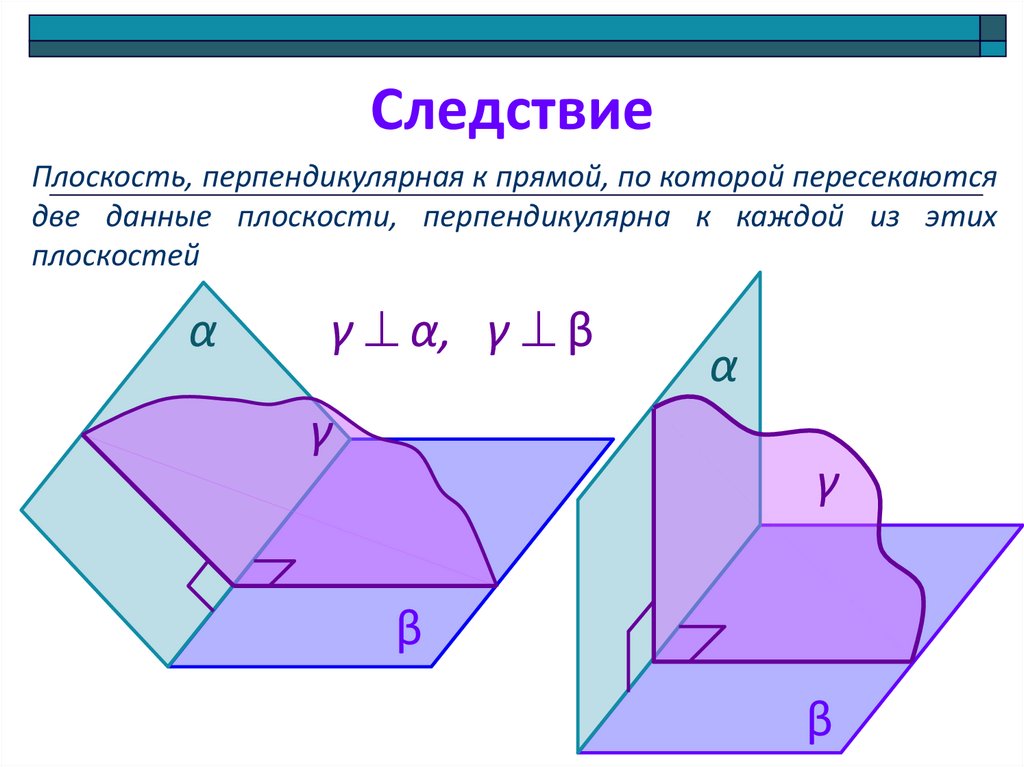
12. Следствие

Плоскость, перпендикулярная к прямой, по которой пересекаются
две данные плоскости, перпендикулярна к каждой из этих
плоскостей
α
γ α, γ β
γ
α
γ
β
β

13.

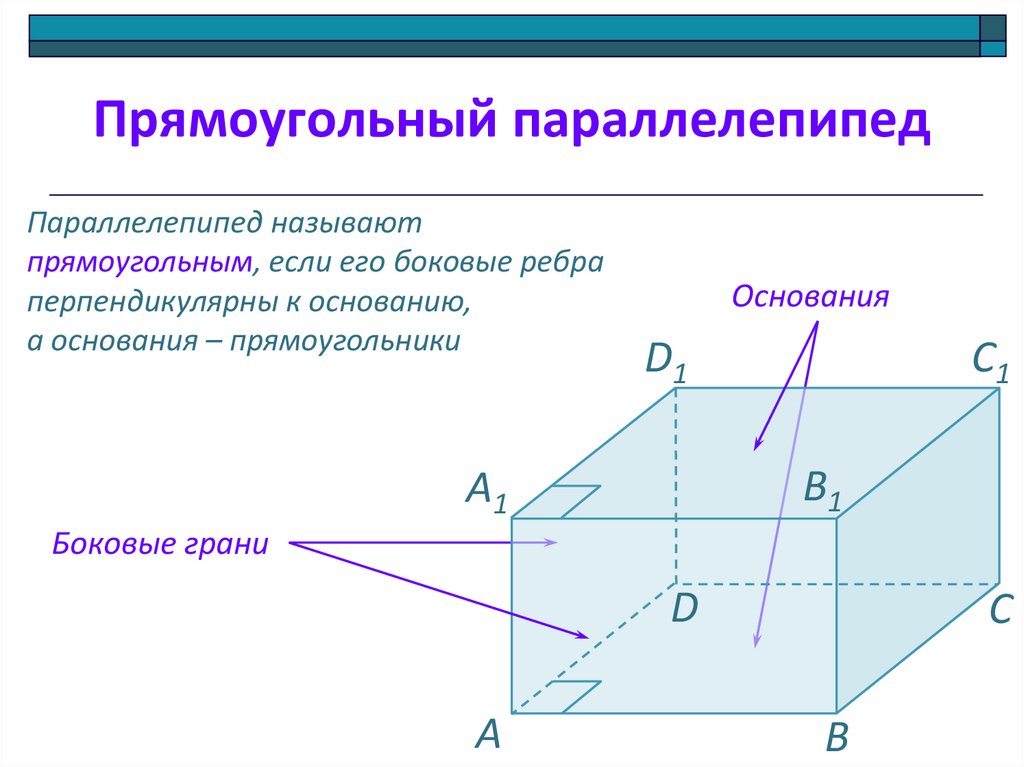
Прямоугольный параллелепипед
Параллелепипед называют
прямоугольным, если его боковые ребра
перпендикулярны к основанию,
а основания – прямоугольники
Основания
D1
C1
B1
А1
Боковые грани
D
А
C
B

14.

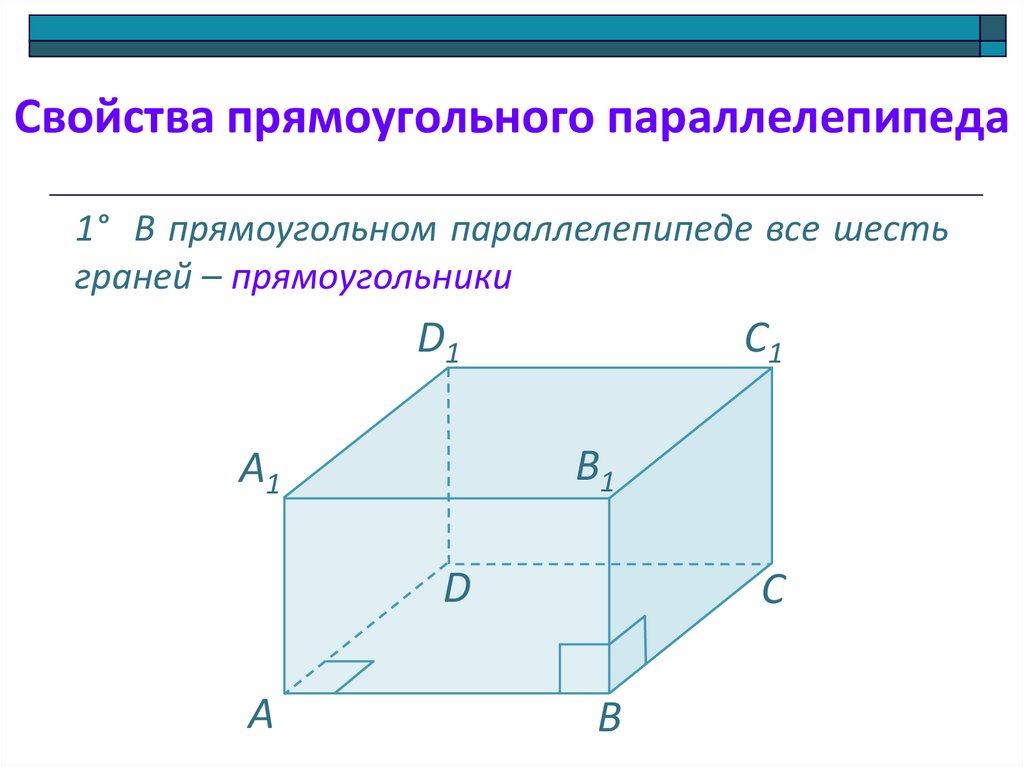
Свойства прямоугольного параллелепипеда
1° В прямоугольном параллелепипеде все шесть
граней – прямоугольники
D1
C1
B1
А1
D
А
C
B

15.

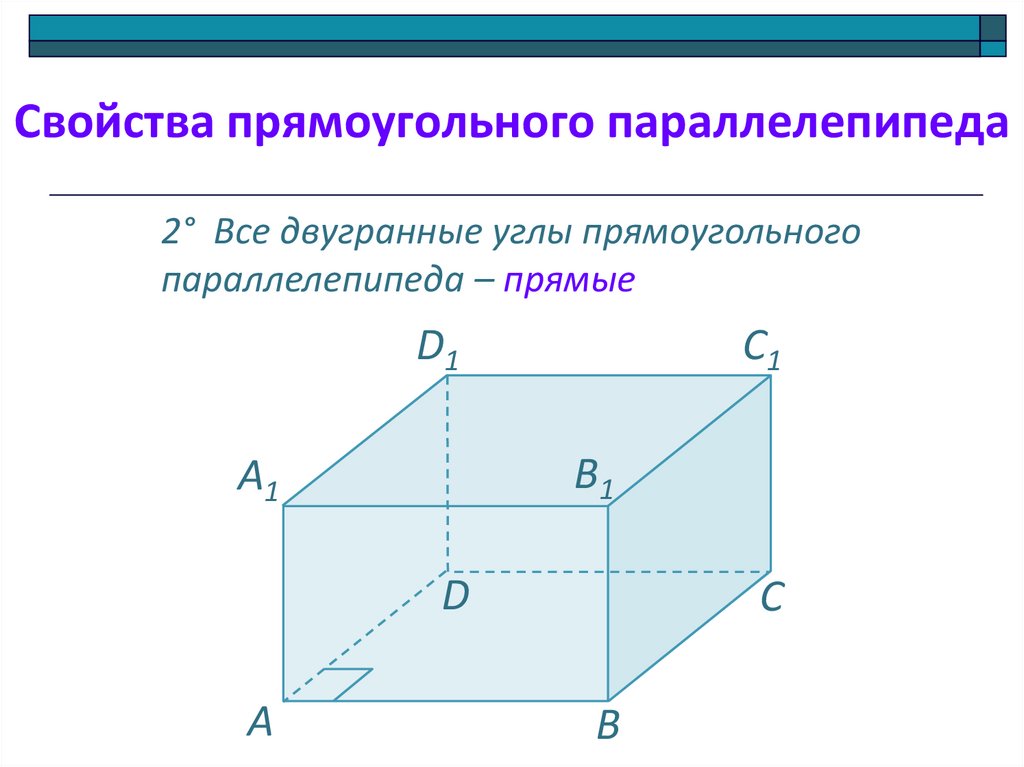
Свойства прямоугольного параллелепипеда
2° Все двугранные углы прямоугольного
параллелепипеда – прямые
D1
C1
B1
А1
D
А
C
B

16.

Измерения прямоугольного
параллелепипеда
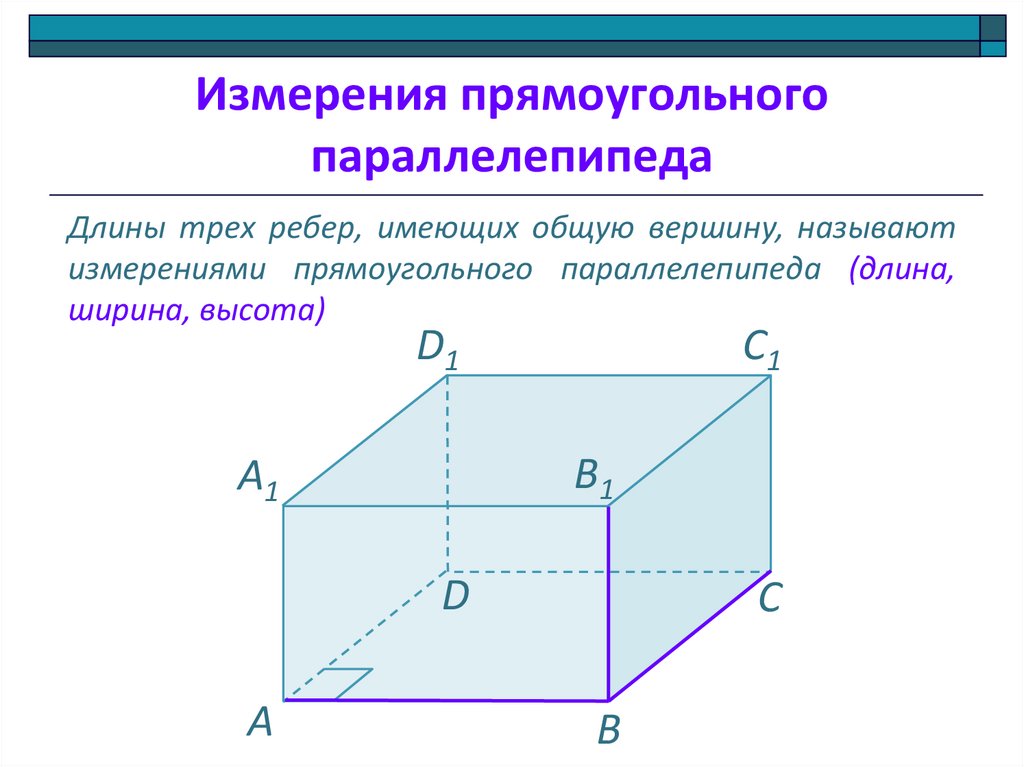
Длины трех ребер, имеющих общую вершину, называют
измерениями прямоугольного параллелепипеда (длина,
ширина, высота)
D1
C1
B1
А1
D
А
C
B

17.

Теорема о диагонали прямоугольного
параллелепипеда
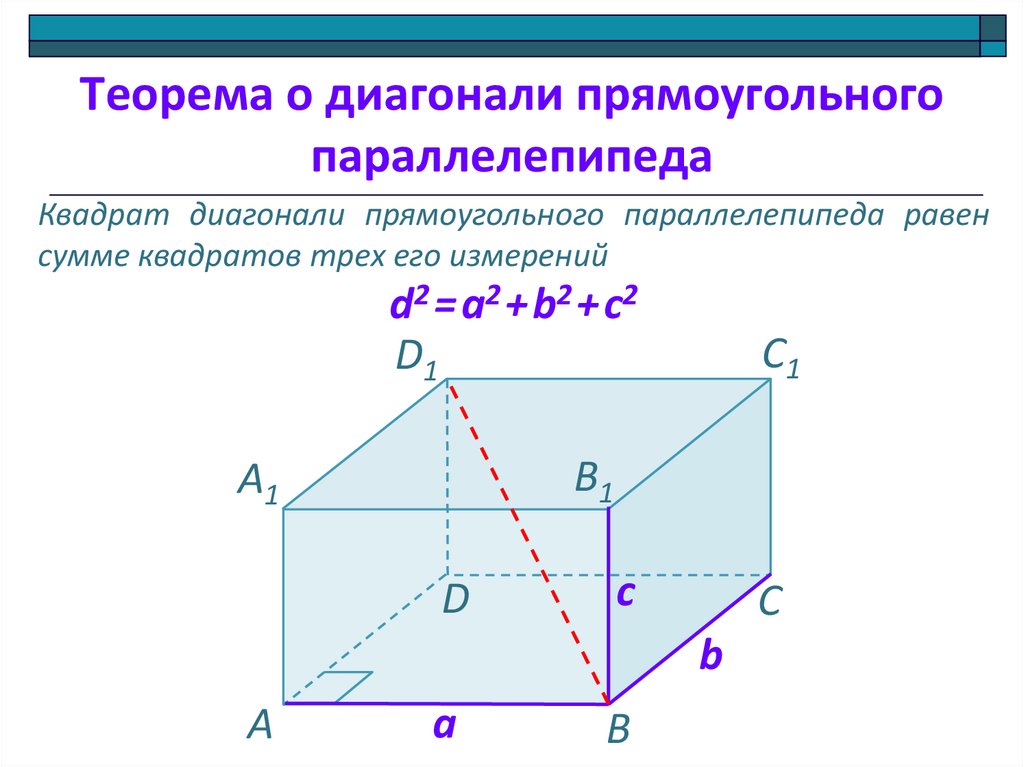
Квадрат диагонали прямоугольного параллелепипеда равен
сумме квадратов трех его измерений
d2 = a2 +b2 +c2
D1
C1
B1
А1
D
c
C
b
А
a
B

18.

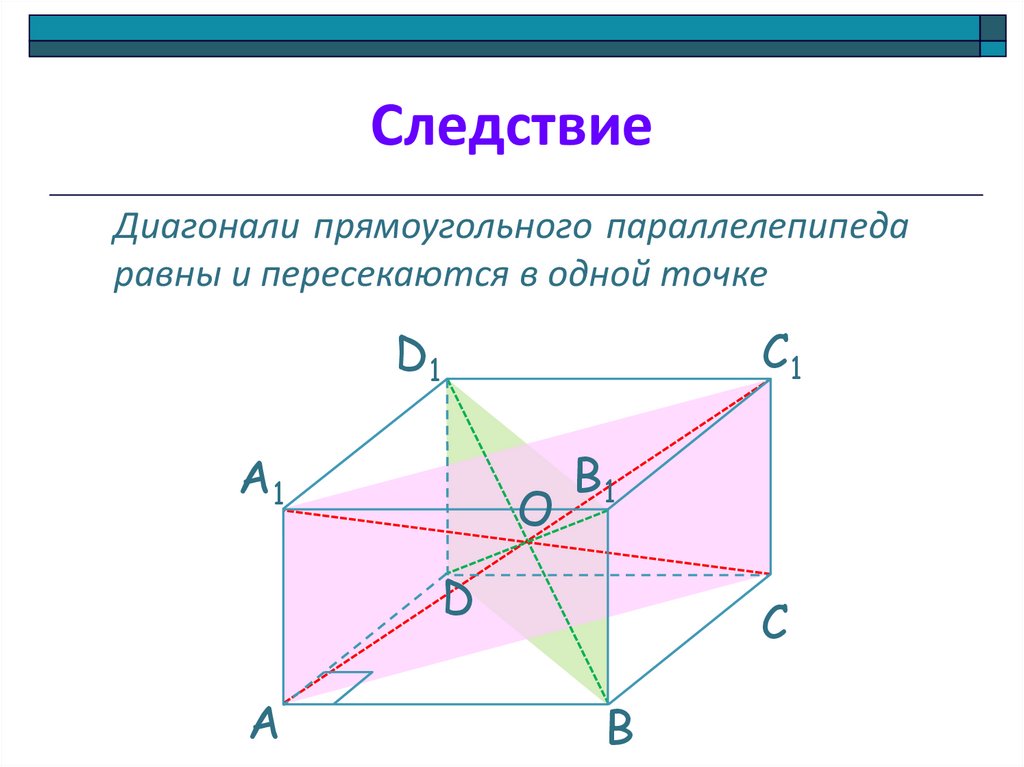
Следствие
Диагонали прямоугольного параллелепипеда
равны и пересекаются в одной точке
C1
D1
А1
О
B1
D
А
C
B

19.

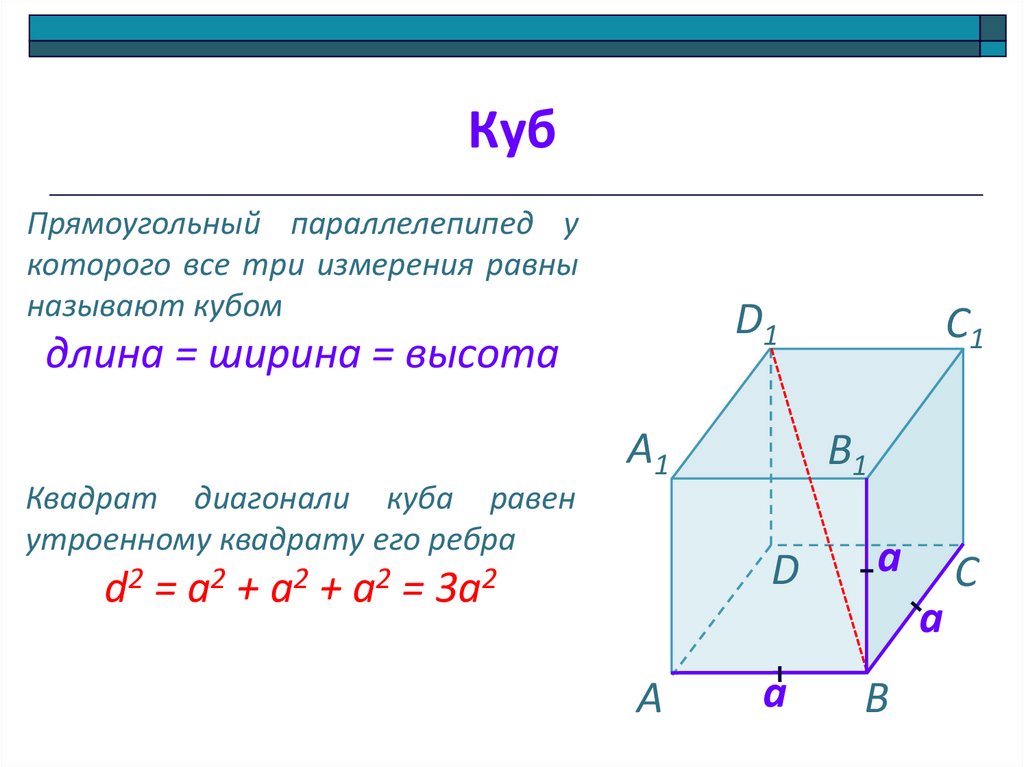
Куб
Прямоугольный параллелепипед у
которого все три измерения равны
называют кубом
D1
длина = ширина = высота
А1
Квадрат диагонали куба равен
утроенному квадрату его ребра
d2
=
a2
+
а2
+
а2
=
B1
D
3a2
C1
a
C
a
А
a
B