Similar presentations:
Двугранный угол. Угол между плоскостями
1. Двугранный угол. Угол между плоскостями.
2. Цель урока:
• Ввести понятие двугранного угла иего линейного угла
• Рассмотреть задачи на применение
этих понятий
• Сформировать конструктивный
навык нахождения угла между
плоскостями
3. Основные понятия
• Прямая а разделяет плоскостьна две полуплоскости
a
α
4.
Общая граница полуплоскостей аназывается ребром двугранного угла.
Полуплоскости, образующие двугранный
угол, называются его гранями.
Двугранным углом
называется фигура,
образованная
прямой а и двумя
полуплоскостями с
общей границей а, не
прилежащими одной
плоскости.
а
β
α
5. Назовите предметы, имеющие форму двугранного угла
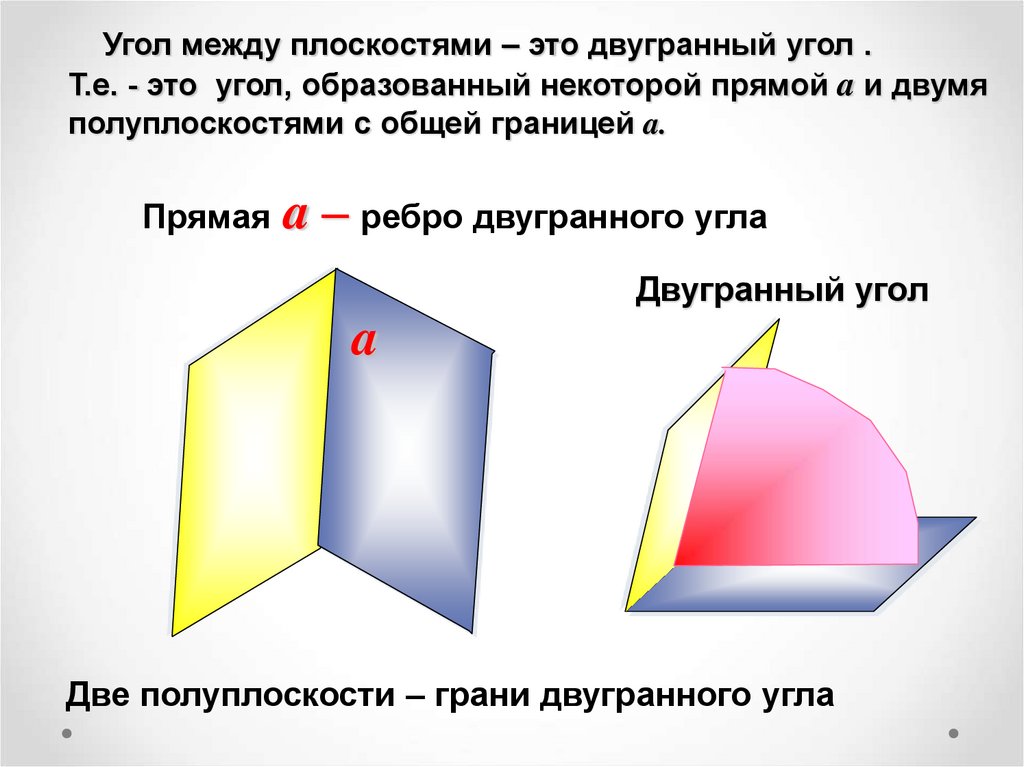
6.
Угол между плоскостями – это двугранный угол .Т.е. - это угол, образованный некоторой прямой a и двумя
полуплоскостями с общей границей a.
Прямая a – ребро двугранного угла
Двугранный угол
a
Две полуплоскости – грани двугранного угла
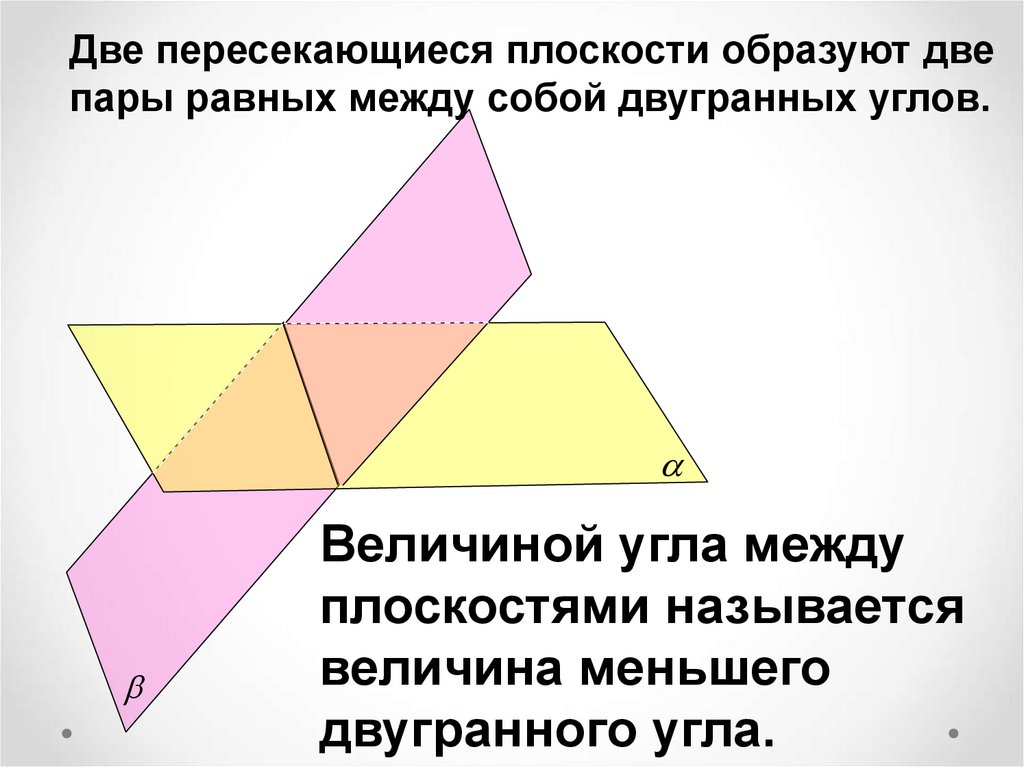
7.
Две пересекающиеся плоскости образуют двепары равных между собой двугранных углов.
Величиной угла между
плоскостями называется
величина меньшего
двугранного угла.
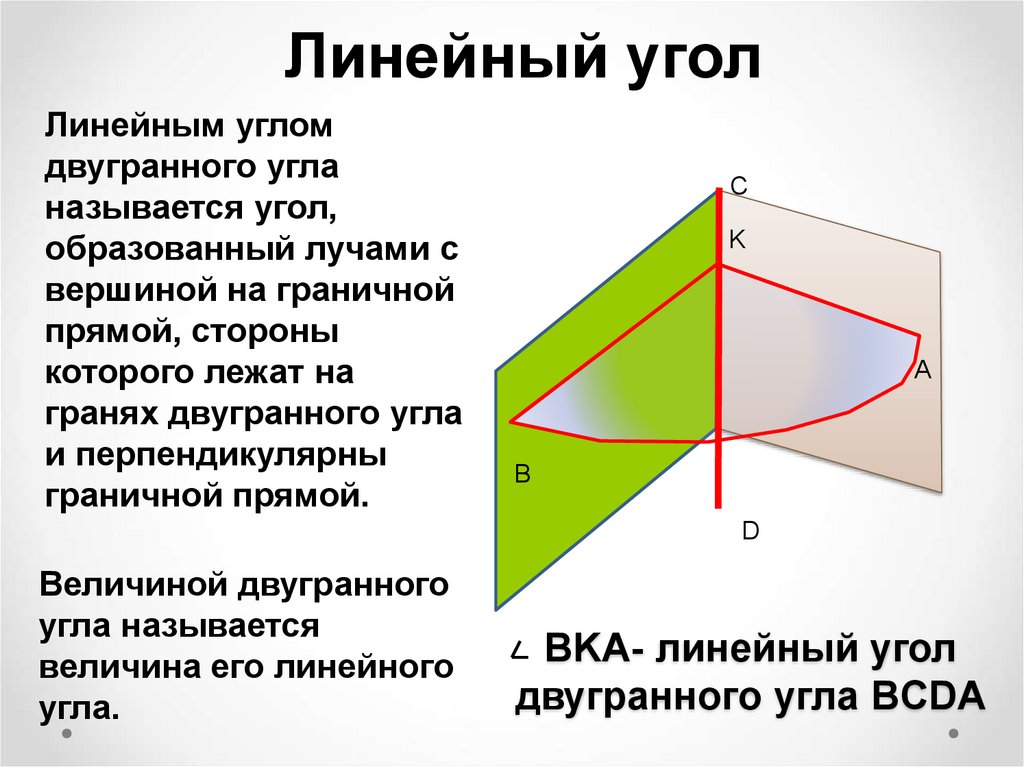
8. BKA- линейный угол двугранного угла BCDA
Линейный уголЛинейным углом
двугранного угла
называется угол,
образованный лучами с
вершиной на граничной
прямой, стороны
которого лежат на
гранях двугранного угла
и перпендикулярны
граничной прямой.
C
K
А
В
D
Величиной двугранного
угла называется
величина его линейного
угла.
BKA- линейный угол
двугранного угла BCDA
9.
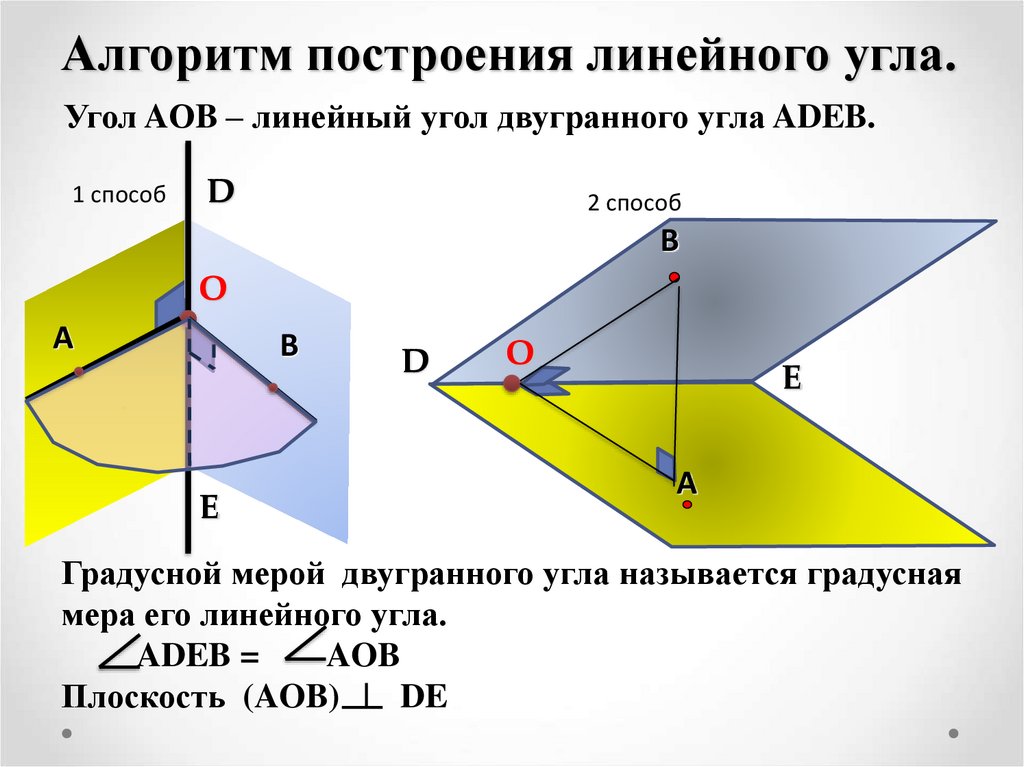
Алгоритм построения линейного угла.Угол AОB – линейный угол двугранного угла ADEB.
1 способ
D
2 способ
B
O
A
B
E
D
O
E
A
Градусной мерой двугранного угла называется градусная
мера его линейного угла.
ADEB =
AOB
Плоскость (AOB)
DE
10.
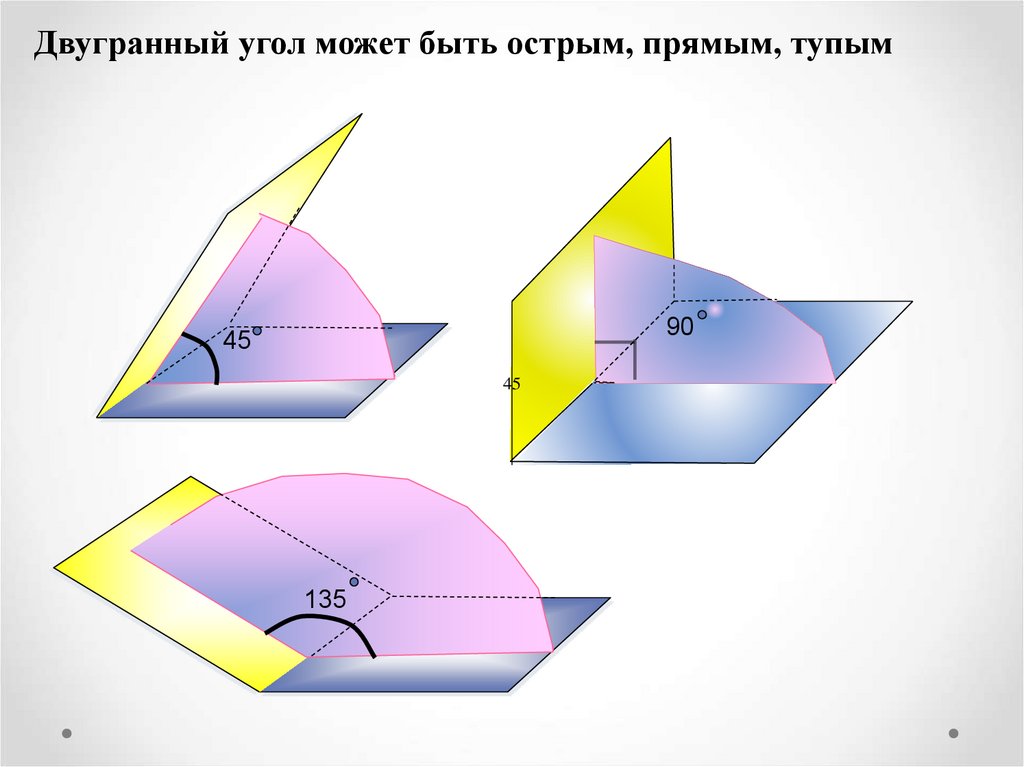
Двугранный угол может быть острым, прямым, тупым90
45
45
135
11.
Все линейные углы двугранного угла равныдруг другу.
Лучи ОА и О1А1 –
сонаправлены
O
А
В
Лучи ОВ и О1В1 –
сонаправлены
Углы АОВ и А1О1В1
равны,
как углы с
сонаправленными
сторонами
O
А1
1
В1
12.
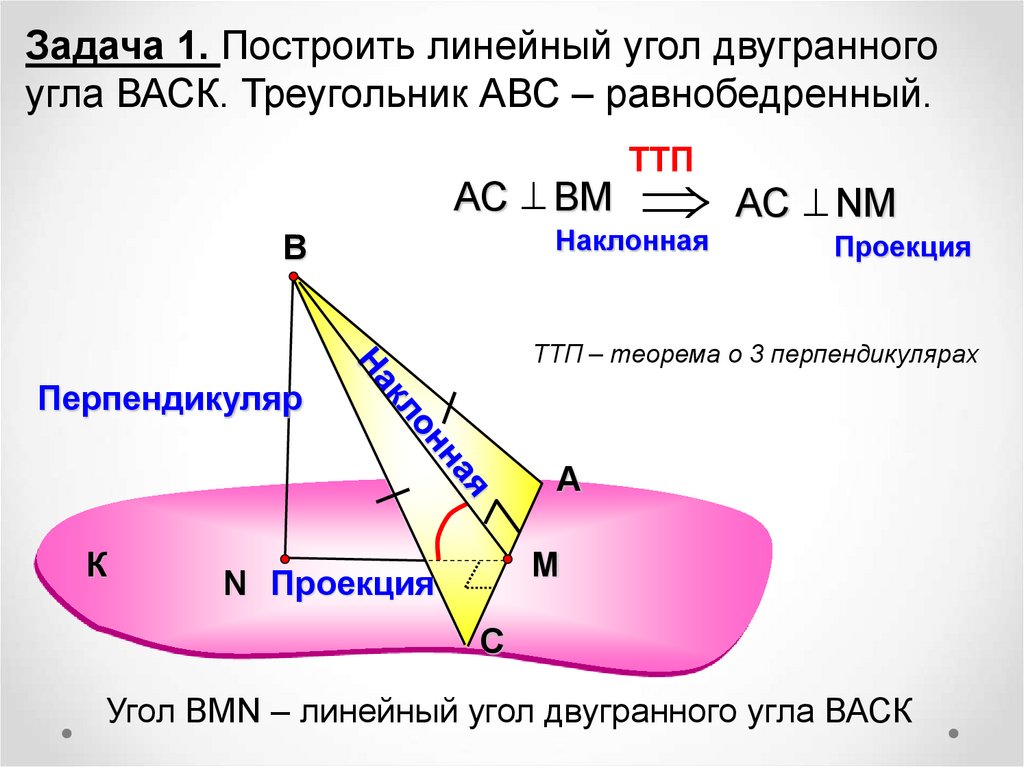
Задача 1. Построить линейный угол двугранногоугла ВАСК. Треугольник АВС – равнобедренный.
TTП
В
АС ВМ АС NМ
Hаклонная
Проекция
ТТП – теорема о 3 перпендикулярах
Перпендикуляр
А
К
M
N Проекция
С
Угол ВMN – линейный угол двугранного угла ВАСК
13.
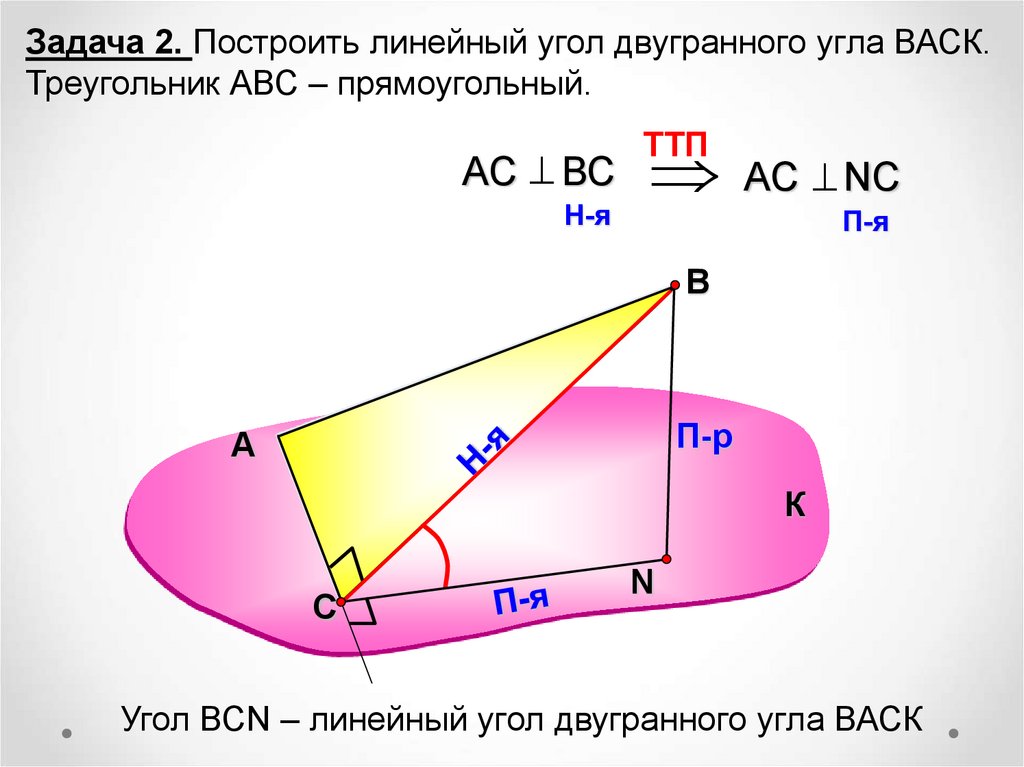
Задача 2. Построить линейный угол двугранного угла ВАСК.Треугольник АВС – прямоугольный.
АС ВС
H-я
АС NС
TTП
П-я
В
П-р
А
К
С
N
Угол ВСN – линейный угол двугранного угла ВАСК
14.
Задача 3. Построить линейный угол двугранного угла ВАСК.Треугольник АВС – тупоугольный.
АС ВS
H-я
АС NS
TTП
П-я
В
П-р
А
К
С
S
N
Угол ВSN – линейный угол двугранного угла ВАСК
15.
Задача 4. Построить линейный угол двугранного углаВАСК. АВСD – четырехугольник, АС – диагональ, АС=1;
ВС=2; АВ= 5 ОбрTTП
АС ВС
АС NС
П-я
H-я
В
5
А
П-р
2
1
К
N
С
D
Угол ВСN – линейный угол двугранного угла ВАСК
16.
Задача 5. Построить линейный угол двугранногоугла ВАСК. АВСD – четырехугольник, АС –
диагональ; АС=5, ВС= 6, АВ= 9.
АС ВS
ОбрTTП
АС NS
П-я
H-я
В
9
А
6
5
П-р
К
С
S
N
D
Угол ВSN – линейный угол двугранного угла ВАСК
17.
P1) ADC 1200 CDH 600
2)РС АВС , СH AD, поТТП PH AD
CH
3) Из DCH: sin
;
CD
CH
sin 60 0
6
В
С
120
А
D
РНС линейный
6 3
CH 6 sin 60
3 3
2
9
4) Из PCH: tgPHC
3 , PHC 600
3 3
0
5) S ABCD CH AD 8 3 3 24 3
H
18.
Задача 7. (Решение с помощью построения линейного угла)1) Построим плоскость СBА1
С1 Перпендикуляр из точки А1на
плоскость (АВС) – точка А, А1D –
наклонная, АD проекция наклонной на
(АВС). Тогда угол АDА1 – это
линейный угол двугранного угла
между плоскостями (АВС) и ( ВА1С).
2
А1
В1
2) Из AВС:
5
AD
С
А
22 1
3.
3) Из A1ВD:
D
A1 D
В
AB 2 BD 2
A1 B 2 BD 2
5 1
4 2.
4) Из A1AD:
AD
cos
;
A1 D
3
cos
2
Из
A1AD:
30
19.
Задача 8. (решение построением параллельной плоскости)В кубе ABCDA1B1C1D1 точки E и F середины ребер соответственно
A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
1) Заменим плоскость DBB1 на параллельную плоскость FEKL. Угол
между плоскостями AEF и BDD1 равен углу между плоскостями AEF и
D1
C1 2) Ребро двугранного угла – FE.
FEK.
F
3) Строим линейный угол
О E
двугранного угла AFEK.
A1
4) Найдем два элемента
B1
треугольника AOP. Пусть ребро
куба равно a (или 1).
5) Из APK:
6) Из AОP:
a
AP
AP
cos 450
;
tgAOP
;
D
AK
C
OP
2 AP
L
a 2
;
a
P
tgAOP
: a;
a
2
4
2
2
a
A 450 a K
B
AP
;
2
2
tgAOP
.
2 2
4
a 2
AP
.
4
20.
• Задача 9. В прямоугольномпараллелепипеде ABCDA1B1C1D1 точка N –
середина ребра CD , AB = 3 , BC = 2 , BB1 = 2.
Найдите угол между плоскостями AB1N и
ABC .
• Задача 10. В правильной четырехугольной
пирамиде SABCD с основанием ABCD
сторона основания равна 3, а боковое
ребро равно 5. Найдите угол между
плоскостями ABC и ACM, где точка M делит
ребро BS так, что BM : MS = 2 : 1.
21.
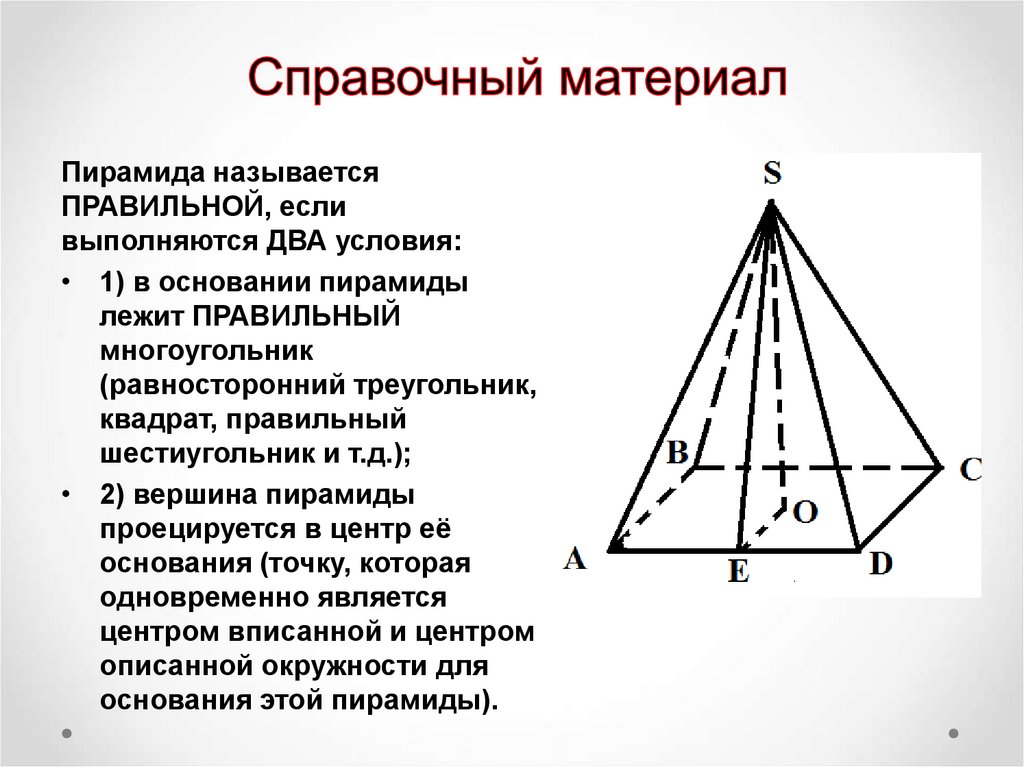
Пирамида называетсяПРАВИЛЬНОЙ, если
выполняются ДВА условия:
• 1) в основании пирамиды
лежит ПРАВИЛЬНЫЙ
многоугольник
(равносторонний треугольник,
квадрат, правильный
шестиугольник и т.д.);
• 2) вершина пирамиды
проецируется в центр её
основания (точку, которая
одновременно является
центром вписанной и центром
описанной окружности для
основания этой пирамиды).













 mathematics
mathematics








