Similar presentations:
Динамика вращательного движения. Момент силы
1.
ДИНАМИКА ТВЕРДОГО ТЕЛАМомент силы
Момент силы
относительно
точки О:
r
r r
M = éë r , F ùû
2.
Момент силы, взятыйотносительно точки О, находится
как векторное произведение
радиус-вектора, проведенного из
точки О в точку приложения
силы, на эту силу.
3.
M = r × F × sin al = r × sin a
l
l - плечо силы
M = F ×l
4.
Направление вектора моментасилы находим по правилу
правого винта.
Этот вектор перпендикулярен и
силе, и радиус-вектору.
r
r r r
M ^ F,M ^ r
5.
Момент силы, вычисленныйотносительно точки, характеризует
способность силы вызывать поворот
вокруг этой точки.
r
M
O
r
r
r
M =0
r
F
l
O
r
F
r
r
r
M ¹0
6.
Другой способ вычисления момента силыl
7.
Момент силы относительно оси8.
Момент силы относительно оси z– это скалярная величина, равная
r
проекции на ось z вектора M,
найденного относительно
произвольной точки этой оси.
9.
M = r × Ftr × sinq = R
M z = M × sinq
M z = Ft × R
10.
Момент сил взаимодействияr
f12
l
O
r
r1
r
r2
r
f 21
r
r
f12 = - f 21
r
r
M 12 = - M 21
r
r
r
M = M 12 + M 21 = 0
11.
Момент пары силПара сил - две равные по величине,
противоположные по направлению силы,
не действующие вдоль одной прямой.
l
M = F ×l
l - плечо пары
12.
Момент импульсаМомент импульса МТ
относительно точки
О:
r r r
r r
L = [ r , p ] = [ r , mv ]
m
l – плечо импульса
L = rp sin a = pl
Направление
определяется также по
правилу правого винта.
13.
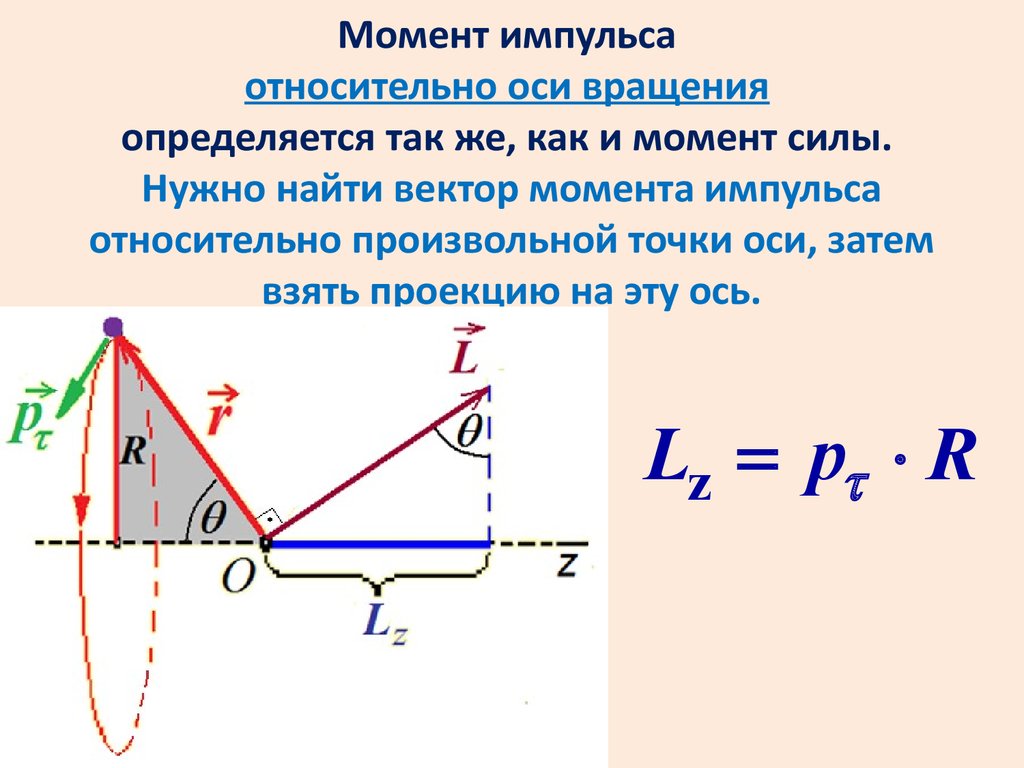
Момент импульсаотносительно оси вращения
определяется так же, как и момент силы.
Нужно найти вектор момента импульса
относительно произвольной точки оси, затем
взять проекцию на эту ось.
Lz = pt × R
14.
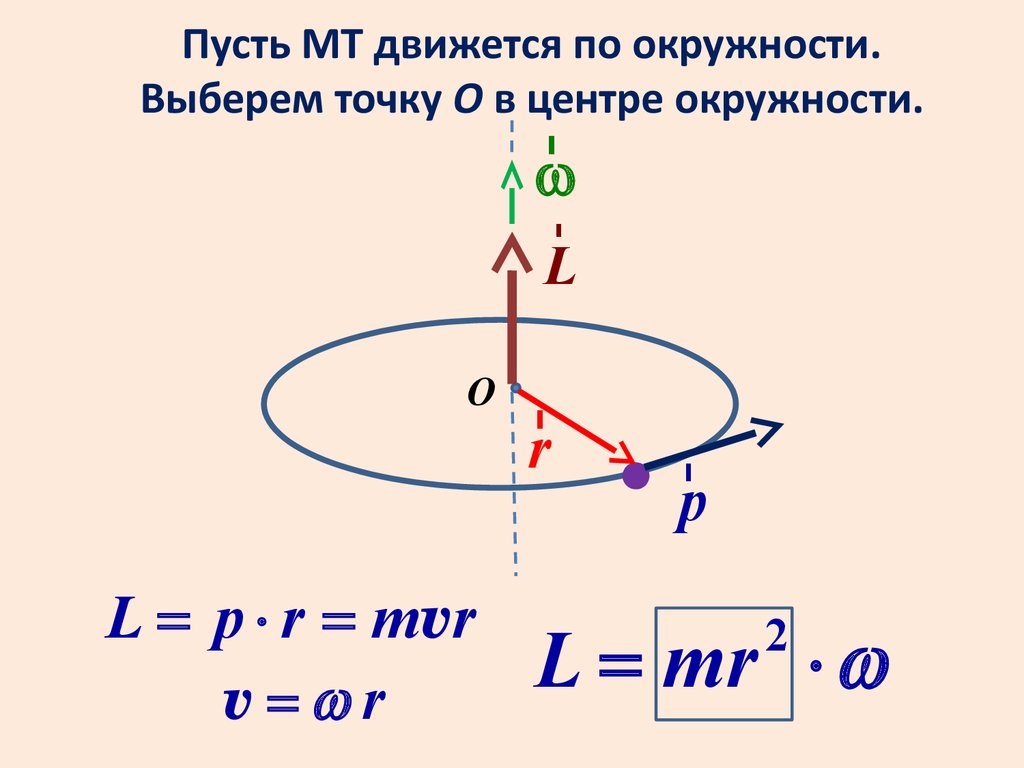
Пусть МТ движется по окружности.Выберем точку О в центре окружности.
r
w
r
L
О
L = p × r = mvr
v=wr
r
r
r
p
L = mr × w
2
15.
Моментом инерции МТназывают произведение ее
массы на квадрат расстояния
до оси вращения.
I = mr
2
16.
Если МТ движется по окружностирадиуса r, то ее момент импульса
r
r
L = Iw
[ I ] = кг · м
2
17.
Момент инерции твердого телаМомент инерции тела относительно
данной оси – это величина, равная сумме
произведений элементарных масс на
квадраты их расстояний от данной оси.
I = å Dmi ri
2
i
или
I = ò r × dm
2
V
18.
Момент импульса твердого телаРазобьем тело на систему материальных точек
массой Dmi . Найдем момент импульса отн. оси z.
rri
z
i
Lz = å Lz,i
i
19.
Lz,i = Dmi × w × riLz = w å Dmi × ri
2
2
i
Lz = I zw
Iz – момент инерции тела отн. оси z.
20.
Для однородного симметричноготела, вращающегося вокруг оси
симметрии, справедливо векторное
равенство:
r
r
L = Iw
I – момент инерции тела
относительно оси симметрии
21.
Момент инерции телаопределяется его
размерами, формой,
распределением и
величиной массы, а
также положением оси
вращения.
22.
Момент инерции кольцаI=
ò
r × dm
2
по кольцу
r = R = const .
I = R ò dm
2
по кольцу
I C = mR
2
23.
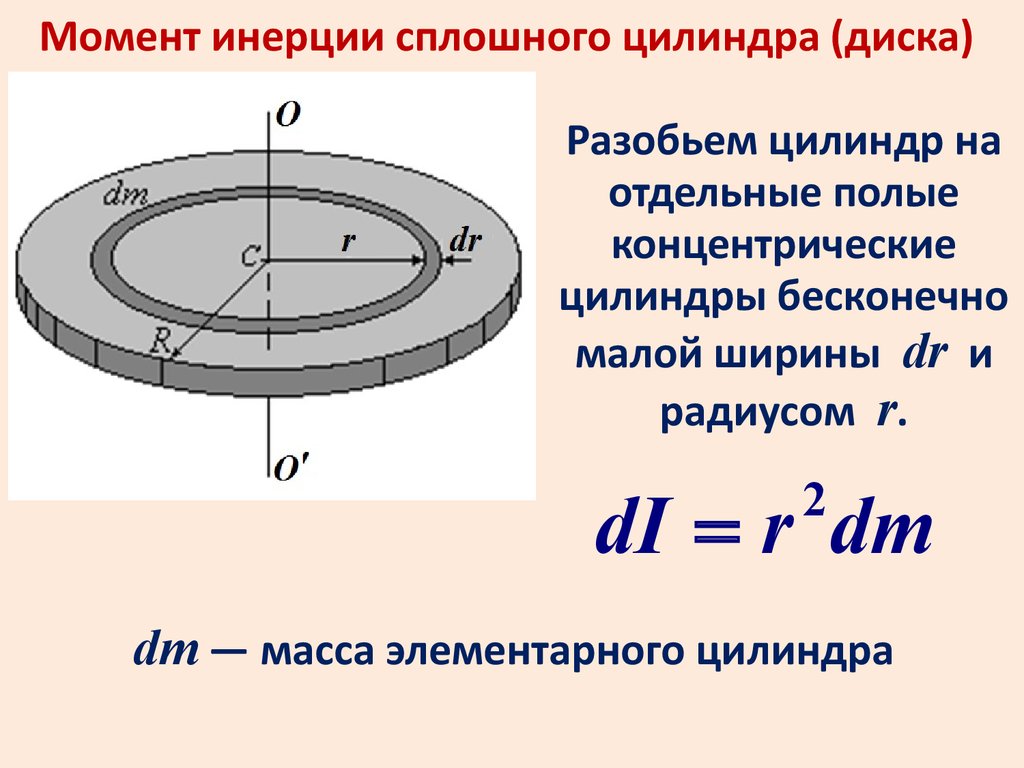
Момент инерции сплошного цилиндра (диска)Разобьем цилиндр на
отдельные полые
концентрические
цилиндры бесконечно
малой ширины dr и
радиусом r.
dI = r dm
2
dm — масса элементарного цилиндра
24.
dm =ρdV = ρ ×dS ×hdS = 2p r × dr
dm = 2pr h × rdr
m
r=
2
pR h
25.
RR
I = ò r dm = ò 2pr h r dr
2
0
3
0
R
r
I = 2pr hò r dr = 2pr h ×
4
0
3
pr hR
=
0
2
4 R
1
2
I C = mR
2
4
26.
Моменты инерции IC некоторых однородных твердых тел27.
Теорема ШтейнераМомент инерции относительно произвольной
оси вращения равен сумме момента инерции
тела относительно параллельной оси
вращения, проходящей через центр инерции
тела, и произведения массы тела на квадрат
расстояния между осями.
I = I C + ma
2
28.
Применение теоремы Штейнера1
2
Для стержня I C =
ml
12
Найдем момент инерции стержня относительно
оси, проходящей через его конец:
l
a=
2
2
2
2
2
ml
ml
4ml
ml
2
I = I C + ma =
+
=
=
12
4
12
3
1 2
I = ml
3




















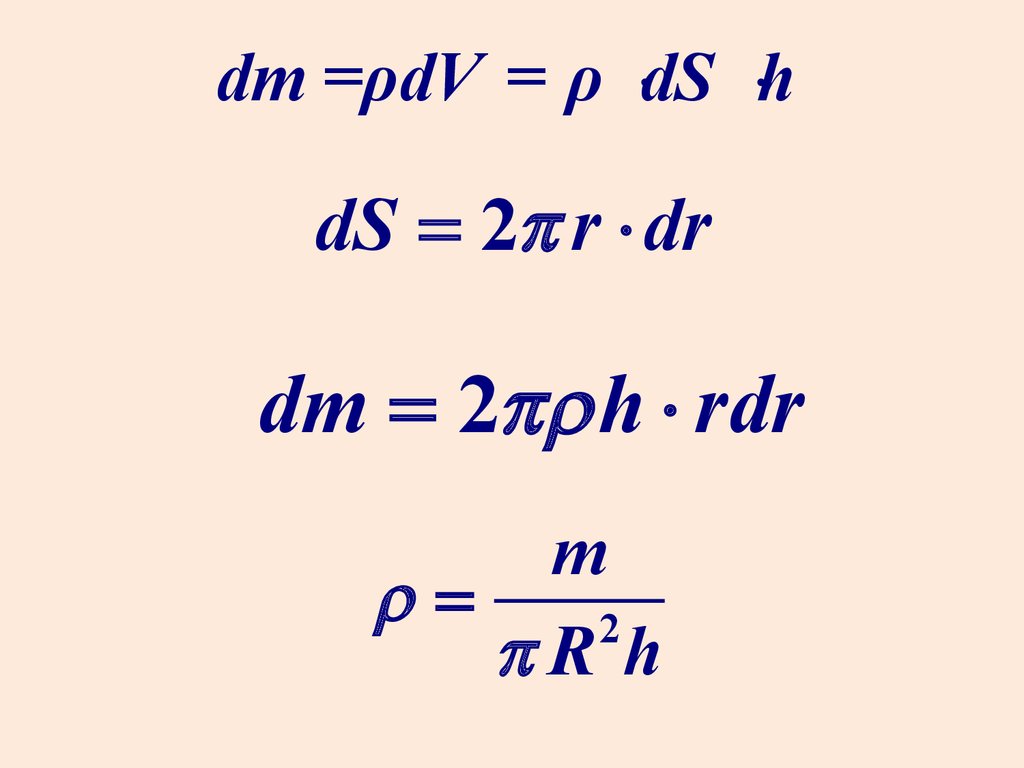




 physics
physics