Similar presentations:
Динамика вращательного движения
1.
Лекция 3.Кафедра физики
ПЛАН ЛЕКЦИИ.
1. Динамика вращательного движения твердого тела:
момент импульса относительно центра;
момент силы относительно центра;
момент импульса относительно оси;
момент силы относительно оси;
момент инерции тела
2. Закон сохранения момента импульса
3. Силы инерции: центробежная и сила Кориолиса
Общая физика. Раздел "Основы классической механики"
1
2.
ДИНАМИКА ВРАЩАТЕЛЬНОГОДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Кафедра физики
Твердое тело - это совокупность точек, расстояние между
которыми не меняется.
Число независимых координат, однозначно определяющих положение
тела или системы тел в пространстве, называется числом степеней
свободы тела или системы тел
Центр инерции системы движется так, как двигалась бы частица с
массой, равной суммарной массе системы, под действием силы,
равной суммарной внешней силе.
Движение центра инерции системы можно отождествлять с
поступательным движением системы как целого.
Общая физика. Раздел "Основы классической механики"
2
3.
ДИНАМИКА ВРАЩАТЕЛЬНОГОДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Кафедра физики
Рассмотрим
важнейшие
динамические
характеристики
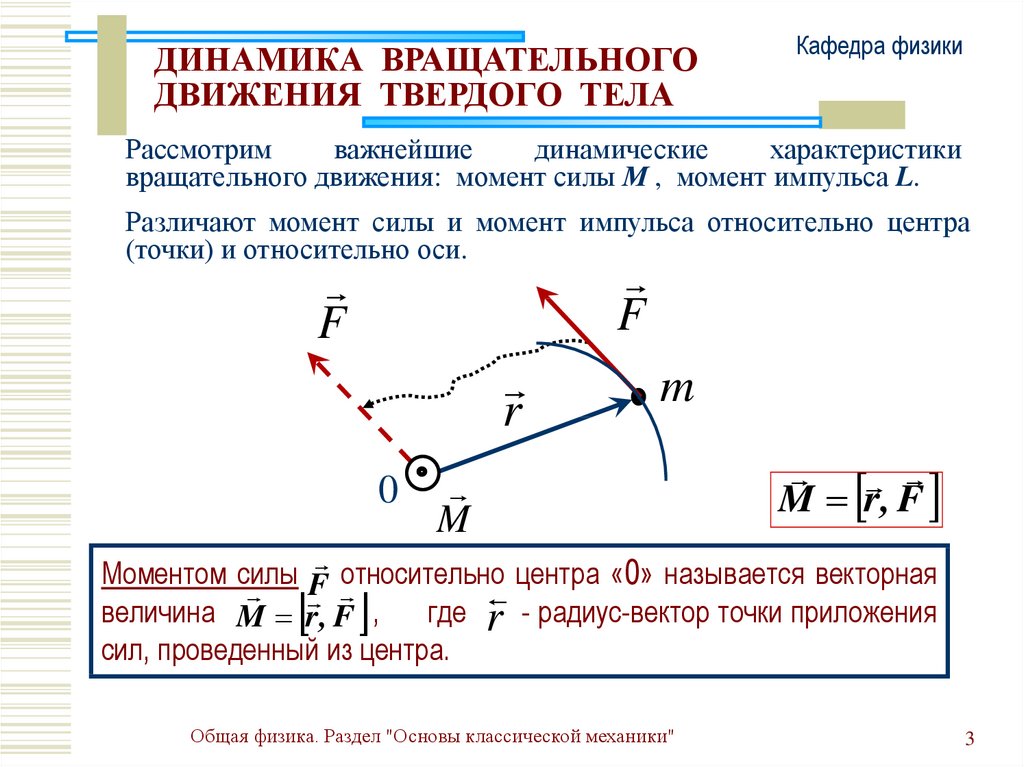
вращательного движения: момент силы М , момент импульса L.
Различают момент силы и момент импульса относительно центра
(точки) и относительно оси.
F
F
r
m
0
M
M r, F
Моментом силы
относительно
центра «0» называется векторная
F
величина M r , F ,
где r - радиус-вектор точки приложения
сил, проведенный из центра.
Общая физика. Раздел "Основы классической механики"
3
4.
ДИНАМИКА ВРАЩАТЕЛЬНОГОДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Кафедра физики
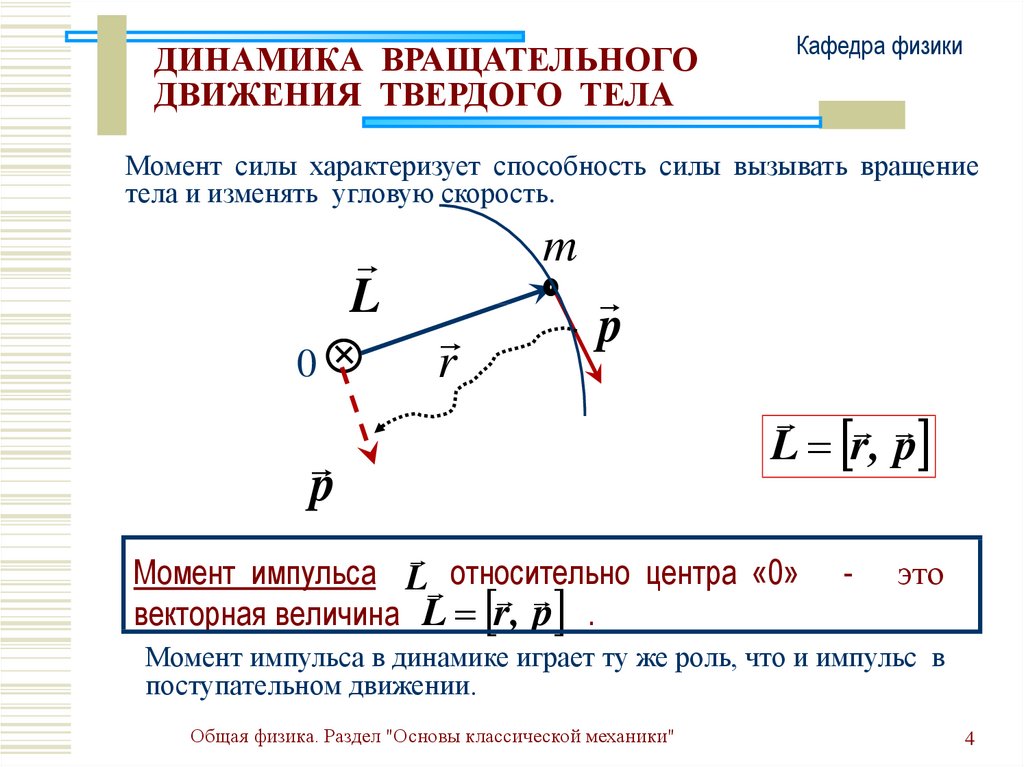
Момент силы характеризует способность силы вызывать вращение
тела и изменять угловую скорость.
L
0
m
r
p
p
L r, p
Момент импульса L относительно центра «0»
векторная величина L r, p .
-
это
Момент импульса в динамике играет ту же роль, что и импульс в
поступательном движении.
Общая физика. Раздел "Основы классической механики"
4
5.
ДИНАМИКА ВРАЩАТЕЛЬНОГОДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Кафедра физики
Плечо импульса и силы относительно точки
l=r sin . - плечо импульса
относительно точки «О»
L l=r sin
α
О
r
m
р
α
Модуль вектора момента импульса
частицы относительно точки O равен:
L p r sin pl
По аналогии модуль вектора момента силы частицы относительно
точки O равен:
M F r sin Fl
Общая физика. Раздел "Основы классической механики"
5
6.
ЗАКОН СОХРАНЕНИЯ МОМЕНТАКафедра физикиИМПУЛЬСА
Суммарный момент импульса
L системы частиц связан с
суммарным моментом M внешних сил, действующих на
систему, уравнением моментов:
d L dt M
второй закон Ньютона, записанный
для моментов импульсов и сил.
M M1 M 2 Mi Mi
i
L L1 L2 Li Li
i 1, 2 , n
i
Момент импульса системы, как и импульс, является
величиной аддитивной
Общая физика. Раздел "Основы классической механики"
6
7.
ЗАКОН СОХРАНЕНИЯ МОМЕНТАКафедра физикиИМПУЛЬСА
Если в
d L dt M
положить M равным нулю, получим:
d L dt 0
Момент импульса замкнутой системы
материальных точек остается постоянным
Общая физика. Раздел "Основы классической механики"
7
8.
ДИНАМИКА ВРАЩАТЕЛЬНОГОДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Кафедра физики
Момент импульса тела относительно оси
Lz J z
Jz
Момент инерции тела относительно оси (аналог массы)
Момент инерции материальной точки массой m, вращающейся
относительно оси вращения по окружности радиуса R
J z mR 2
Момент инерции тела массой m , вращающейся относительно
оси вращения по окружности радиуса R
n
n
J z m i Ri2
m mi
i 1
i 1
Общая физика. Раздел "Основы классической механики"
8
9.
Кафедра физикиДИНАМИКА ВРАЩАТЕЛЬНОГО
ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Формулы для вычисления моментов инерции для стандартных тел
Тело
Ориентация
оси
Полый тонкостенный
цилиндр с радиусом
R и массой m
По оси
цилиндра
Сплошной цилиндр с
радиусом R и массой
m
По оси
цилиндра
m 2
R
2
Полый тонкостенный
цилиндр с радиусом с
внутренним радиусом
R1, внешним радиусом
R2 и массой m
По оси
цилиндра
m 2
R1 R22
2
Диск с радиусом R и
массой m
По оси диска
Общая физика. Раздел "Основы классической механики"
Момент
инерции
mR
2
m 2
R
2
9
10.
Закон сохранения момента импульсаdL z
M z 0, L const . J z const .
dt
Если момент внешних сил относительно неподвижной оси
вращения равен нулю, то момент импульса относительно этой
оси не изменяется с течением времени.
J const . вектор.
Общая физика. Раздел "Основы классической механики"
10
11.
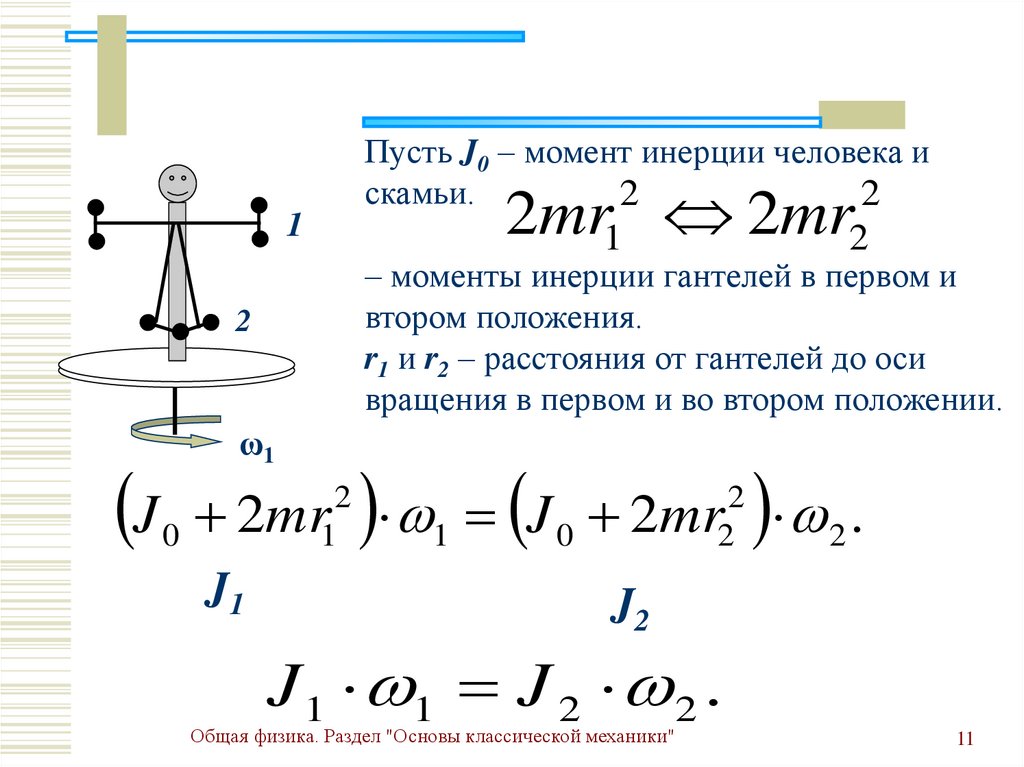
Пусть J0 – момент инерции человека искамьи.
2
2
2mr1 2mr2
1
– моменты инерции гантелей в первом и
втором положения.
r1 и r2 – расстояния от гантелей до оси
вращения в первом и во втором положении.
2
J
ω1
0
2mr 1 J 0 2mr 2 .
2
1
J1
2
2
J2
J 1 1 J 2 2 .
Общая физика. Раздел "Основы классической механики"
11
12.
ДИНАМИКА ВРАЩАТЕЛЬНОГОДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Кафедра физики
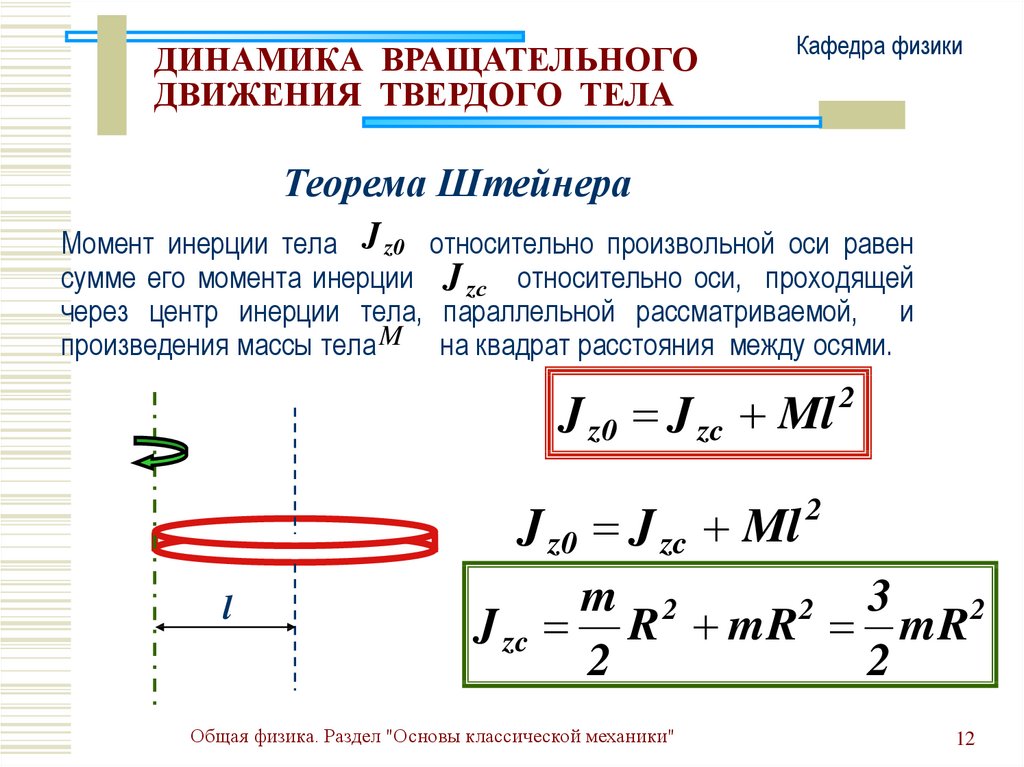
Теорема Штейнера
Момент инерции тела J z0 относительно произвольной оси равен
сумме его момента инерции J zс относительно оси, проходящей
через центр инерции тела, параллельной рассматриваемой, и
произведения массы тела M на квадрат расстояния между осями.
J z0 J zc Ml
2
J z0 J zc Ml
m 2
3
2
2
J zc R mR mR
2
2
2
l
Общая физика. Раздел "Основы классической механики"
12
13.
АНАЛОГИЯ ПОСТУПАТЕЛЬНОГО ИВРАЩАТЕЛЬНО ДВИЖЕНИЙ
Кафедра физики
Поступательное движение
Вращательное движение
Перемещение dS
Угол dφ
Линейная скорость v
Угловая скорость ω
Линейное ускорение a
Угловое ускорение ε
Масса m
Момент инерции J
Импульс p=mv
Момент импульса L=Jω
Сила F
Момент сил M
Уравнение движения F=dp/dt
Уравнение движения M=dL/dt
Уравнение движения a=F/m
Уравнение движения ε =Mz/J
Кинетическая энергия Е=mv2/2
Кинетическая энергия Е=Jω2/2
Работа dA=FdS
Работа dA=Mdφ
Мощность P= Fv
Мощность P = Mω
Общая физика. Раздел "Основы классической механики"
13
14.
НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫОТСЧЕТА
Кафедра физики
Пусть тело движется в инерциальной системе отсчета с ускорением a .
*
Ускорение этого тела в неинерциальной системе отсчета будет a a.
*
a a a
a const
для всех точек пространства поступательно
движущейся неинерциальной системы
a a ( r )
для вращающейся неинерциальной системы
*
*
( r - радиус-вектор, определяющий положение точки относительно
неинерциальной системы отсчета).
Общая физика. Раздел "Основы классической механики"
14
15.
НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫОТСЧЕТА
Кафедра физики
Пусть на тело в неинерционной
системе отсчета действуют силы с
результирующей F .
1
a F
m
- второй закон Ньютона для инерциальной системы
Ускорение тела в неинерциальной системе можно записать в виде
Пусть
1
*
a a a F a
*m
F 0.
Тогда
a a .
Даже при отсутствии внешних сил тело будет двигаться по отношению
к неинерциальной системе отсчета
с ускорением a - так, как если бы
на него действовала сила ma .
Общая физика. Раздел "Основы классической механики"
15
16.
НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫОТСЧЕТА
Кафедра физики
Таким образом, при описании движения в неинерциальных системах
отсчета
можно пользоваться уравнениями Ньютона с учетом сил инерции Fин .
Fин ma
*
ma F Fин
уравнение второго закона Ньютона в неинерциальной
системе отсчета
Общая физика. Раздел "Основы классической механики"
16
17.
Кафедра физикиНЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ
ОТСЧЕТА
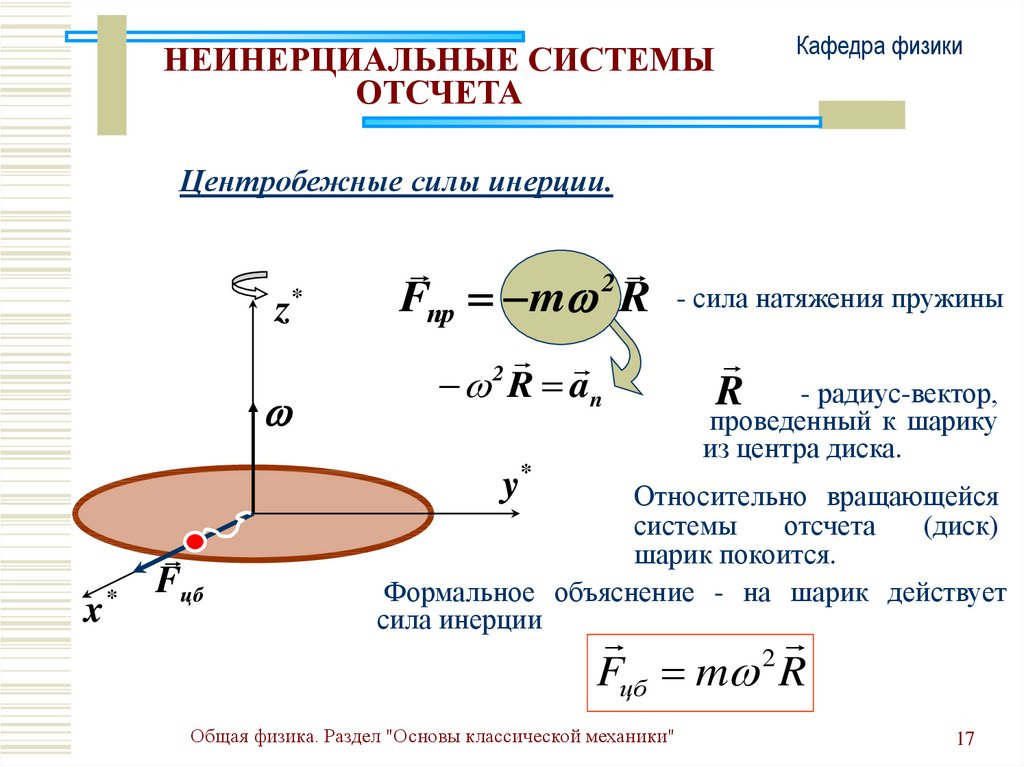
Центробежные силы инерции.
z*
2
Fпр m R
R an
2
- сила натяжения пружины
R
- радиус-вектор,
проведенный к шарику
из центра диска.
y*
x*
Fцб
Относительно вращающейся
системы
отсчета
(диск)
шарик покоится.
Формальное объяснение - на шарик действует
сила инерции
2
Fцб m R
Общая физика. Раздел "Основы классической механики"
17
18.
НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫОТСЧЕТА
Кафедра физики
Центробежные силы инерции.
Приведенная модельная задача сходна с другой модельной задачей –
изучение взаимодействия и движения тел в системе отсчета,
связанной с Землей, вращающейся вокруг своей оси.
Наблюдаемое относительно Земли ускорение свободного падения
тела g обусловлено действием силы
Fg , с которой тело притягивается
Землей, и центробежной силой Fцб . Результирующая этих сил
P Fg Fцб mg
Fg Fцб , P Fg mg
Поскольку
Для массы 1 кг (на экваторе) Fцб max равно 0.035 Н, в то
время, как
Fg 9.8H , т.е. почти в 300 раз больше.
Общая физика. Раздел "Основы классической механики"
18
19.
НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫОТСЧЕТА
Кафедра физики
Центробежные силы инерции. Сила Кориолиса
z*
Fk
B
x * Fцб
O
А
При движении тел во вращающейся системе
отсчета кроме центробежной силы инерции
возникает сила Кориолиса
Если диск не вращается, шарик будет катиться
по прямой ОА со скоростью v *.
y*
Если
привести
диск
во
вращение, траектория движения
шарика - кривая ОВ.
По отношению к вращающейся системе отсчета
шарик ведет себя так, как если бы на него дейстдействовала сила Fk , перпендикулярная направлению
*
скорости v .
Общая физика. Раздел "Основы классической механики"
19
20.
НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫОТСЧЕТА
Кафедра физики
Центробежные силы инерции. Сила Кориолиса
z*
Fk
Fr
- сила Кориолиса
- сила действия ребра на шарик
Примеры проявлений силы Кориолиса:
1. Свободное падение на Землю тел –
отклоняются к востоку от линии отвеса;
x
*
Fk
O
А
Fr
y
*
2. При выстреле из орудия на север,
снаряд отклоняется к востоку в
северном полушарии и к западу а
южном;
3. При стрельбе вдоль экватора на запад снаряд
прижимается к Земле, на восток - поднимается кверху;
3. У рек всегда подмывается правый берег в северном полушарии и левый - в
южном полушарии.
Общая физика. Раздел "Основы классической механики"
20
21.
Кафедра физикиЛекция 3
Лекция окончена.
До следующей встречи.
Желаю успехов в учебе!
Общая физика. Раздел "Основы классической механики"
21
















 physics
physics








