Similar presentations:
Всё по обыкновенным дробям
1. ВСЁ по обыкновенным дробям
6 классУМК: А.Г. Мерзляк
2. Содержание
• Повторим• Основное свойство дроби
• Сокращение дробей
• Приведение дробей к общему знаменателю
• Сравнение дробей
• Сложение и вычитание дробей с разными знаменателями
• Умножение и деление дробей
• Преобразование обыкновенной дроби в десятичную
9.9.17
3. Повторим
«Дробь – число, состоящееиз частей единицы».
9.9.17
4. Повторим
Знаменатель дроби показывает,на сколько равных частей разделено целое.
Числитель показывает, сколько частей взяли.
9.9.17
5. Повторим
aa :b
b
Дроби бывают: правильными и
неправильными
9.9.17
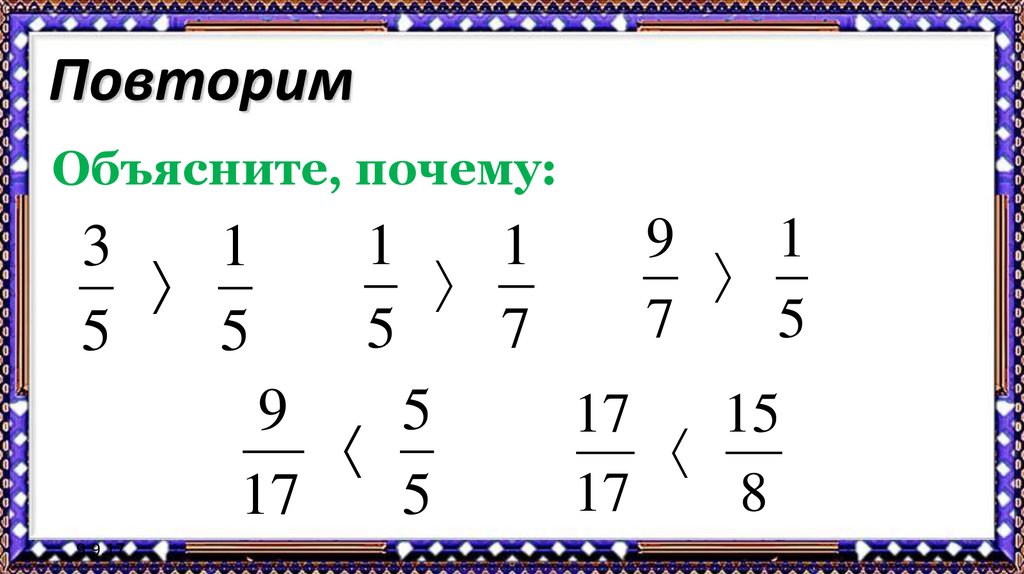
6. Повторим
Объясните, почему:9
1
1
1
7
5
5
7
9
5
17
15
17
8
17
5
3
1
5
5
9.9.17
7. 6 класс
9.9.178. Основное свойство дроби
ЕСЛИ ЧИСЛИТЕЛЬ И ЗНАМЕНАТЕЛЬ ДРОБИУМНОЖИТЬ ИЛИ РАЗДЕЛИТЬ НА ОДНО И ТО
ЖЕ НАТУРАЛЬНОЕ ЧИСЛО, ТО ПОЛУЧИТСЯ
РАВНАЯ ЕЙ ДРОБЬ.
×
1 2 8 40
2 4 16 80
:
9.9.17
9. Основное свойство дроби
ДВЕ РАВНЫЕ ДРОБИ ЯВЛЯЮТСЯРАЗЛИЧНЫМИ ЗАПИСЯМИ ОДНОГО И ТОГО
ЖЕ ЧИСЛА.
4
2
5 10
9.9.17
3
9
15 5
16 2
2
8 1
10. Задание (решаем самостоятельно)
Разделите числитель и знаменатель каждой дробина 9.
45 27 18 72
;
;
;
72 36 45 63
9.9.17
11. Работаем по учебнику
стр.9.9.17
№
12. Сокращение дробей
ДЕЛЕНИЕ ЧИСЛИТЕЛЯ И ЗНАМЕНАТЕЛЯ НА ИХ ОБЩИЙДЕЛИТЕЛЬ, ОТЛИЧНЫЙ ОТ ЕДИНИЦЫ, НАЗЫВАЮТ
СОКРАЩЕНИЕМ ДРОБИ.
2 2:2 1
35 35 : 7 5
6 6:2 3
14 14 : 7 2
12
- несократимая дробь
25
9.9.17
13. Сокращение дробей
• НАИБОЛЬШЕЕ ЧИСЛО, НА КОТОРОЕ МОЖНО СОКРАТИТЬДРОБЬ, - ЭТО НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ ЕЁ
ЧИСЛИТЕЛЯ И ЗНАМЕНАТЕЛЯ.
• У НЕСОКРАТИМОЙ ДРОБИ ЧИСЛИТЕЛЬ И ЗНАМЕНАТЕЛЬ
– ЭТО ВЗАИМНО ПРОСТЫЕ ЧИСЛА
• ПРИ СОКРАЩЕНИИ ДРОБЕЙ ИСПОЛЬЗУЮТ ПРИЗНАКИ
ДЕЛИМОСТИ 150
50 10
2
225
9.9.17
75
15
3
14. Сокращение дробей
• ПРИ СОКРАЩЕНИИ ДРОБЕЙ ТАК ЖЕ ИСПОЛЬЗУЮТРАЗЛОЖЕНИЕ ЧИСЛА НА ПРОСТЫЕ МНОЖИТЕЛИ
3
5 3 3 3
135 5 27
180 18 10 2 3 3 2 5 4
9.9.17
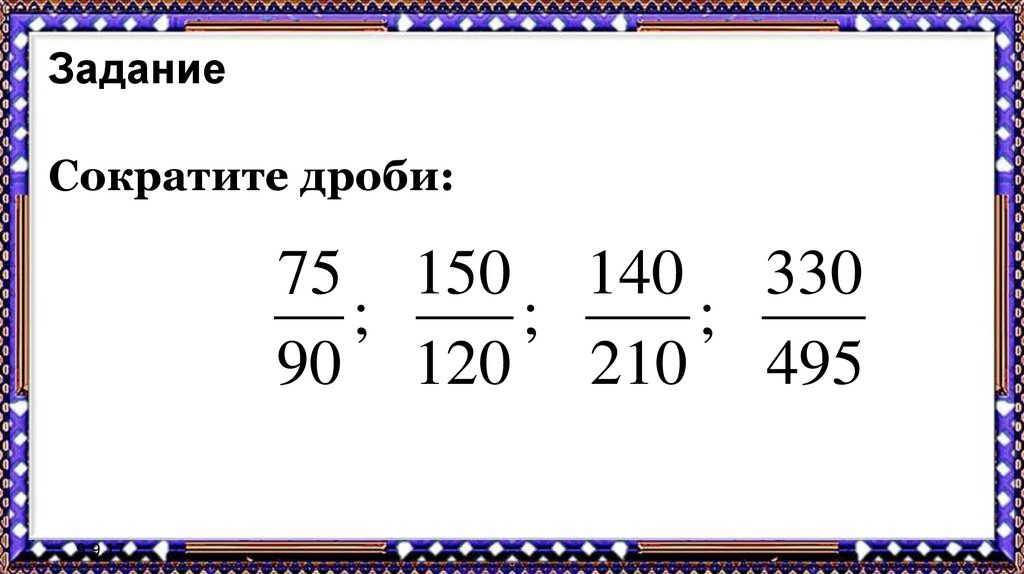
15. Задание
Сократите дроби:75 150 140 330
;
;
;
90 120 210 495
9.9.17
16. Работаем по учебнику
стр.9.9.17
№
17. Приведение дробей к общему знаменателю
ЛЮБЫЕ ДВЕ ДРОБИ (или несколько дробей) МОЖНОПРИВЕСТИ К ОДНОМУ И ТОМУ ЖЕ ЗНАМЕНАТЕЛЮ, ИЛИ,
ИНАЧЕ, К ИХ ОБЩЕМУ ЗНАМЕНАТЕЛЮ.
ОБЩИЙ ЗНАМЕНАТЕЛЬ ДРОБЕЙ – ЭТО ОБЩЕЕ
КРАТНОЕ ЗНАМЕНАТЕЛЕЙ
(Чаще приводят дроби к наименьшему общему
знаменателю, который равен НОК знаменателей
данных дробей)
9.9.17
18. Приведение дробей к общему знаменателю
Например: 5/6 и 3/4 привести к общемузнаменателю
1). Найдём НОК (6;4) = 12
(дополнительный множитель для первой дроби)
2). 12:6 = 2
3). 12:4 = 3 (дополнительный множитель для второй дроби)
4). Числитель и знаменатель каждой дроби
умножаем на дополнительный множитель этой
дроби 5
5 2 10
6
9.9.17
6 2
12
3 3 3 9
4 4 3 12
19. Приведение дробей к общему знаменателю
Чтобы привести дроби к наименьшемуобщему знаменателю, надо:
1) найти НОК знаменателей данных дробей
2) найти дополнительные множители для
каждой дроби (для этого надо разделить общий
знаменатель на знаменатель дроби)
3) умножить числитель и знаменатель каждой
дроби на дополнительный множитель этой
дроби
9.9.17
20. Работаем по учебнику
стр.9.9.17
№
21. Сравнение дробей
Чтобы сравнить дроби с разнымизнаменателями, надо привести их к
общему знаменателю, а затем
применить правило сравнения дробей
с одинаковыми знаменателями
(т.е. та дробь будут больше, у которой
числитель больше).
9.9.17
22. Задание
Сравните дроби2
3
и
3
5
Решение. 1) Приведём дроби к общему знаменателю
2) Найдём дополнительные множители для каждой
дроби: 15 : 3 = 5 (доп. множ. для первой дроби)
15 : 5 = 3 (доп. множ. для второй дроби)
3 3 3 9
3) Получим дроби: 2 2 5 10 и
5 5 3 15
3 3 5 15
10
9
4) Сравним
и
и
делаем
вывод.
15
15
9.9.17
15
23. Задание
Расположите дроби в порядке возрастанияПлан решения:
4 7
8 11
;
;
;
5 10 15 30
1). Привести все дроби к общему
(30)
знаменателю
2). Получить дроби с одинаковым (общим)
знаменателем
(24/30; 21/30; 16/30; 11/30)
3). Сравнить полученные дроби и выполнить
задание
9.9.17
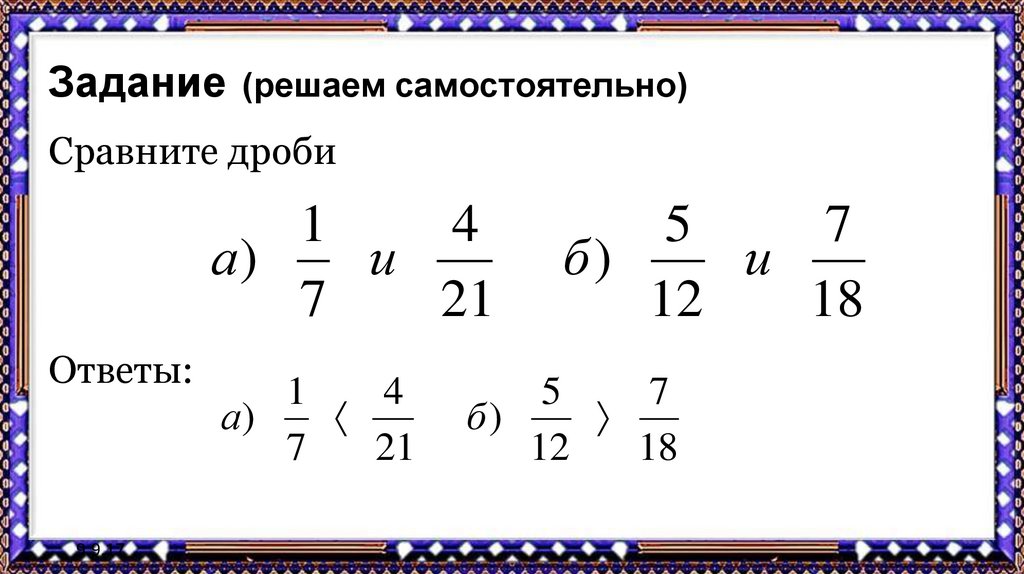
24. Задание (решаем самостоятельно)
Сравните дроби1
4
а)
и
7
21
Ответы:
9.9.17
1
4
а)
7
21
5
7
б)
и
12
18
5
7
б)
12
18
25. Работаем по учебнику
стр.9.9.17
№
26. Сложение и вычитание дробей с разными знаменателями
Чтобы сложить (или вычесть) дроби сразными знаменателями, надо
привести их к общему знаменателю, а
затем применить правило сложения
(вычитания) дробей с одинаковыми
знаменателями.
Т.е.: (формула) стр.???
9.9.17
27. Сложение и вычитание дробей с разными знаменателями
Для дробей, как и для натуральных чисел,выполняются свойства сложения:
а c c a
переместительное св во сложения
в d d в
а c p a c p
сочетательное...
в d g в d g
9.9.17
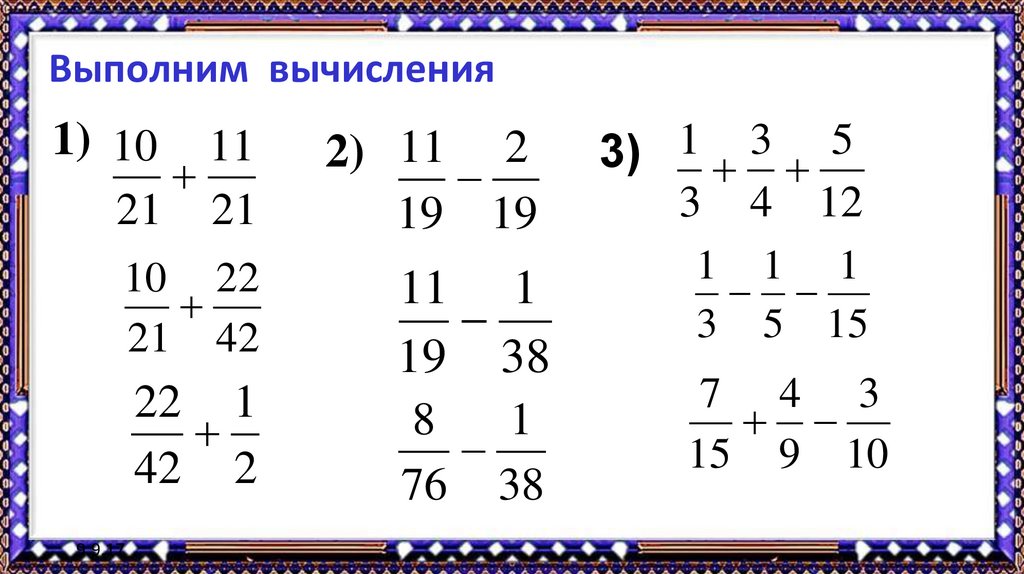
28. Выполним вычисления
1) 10 1121 21
10 22
21 42
22 1
42 2
9.9.17
2) 11 2
19 19
11 1
19 38
8
1
76 38
3) 1 3 5
3
4
12
1 1 1
3 5 15
7 4 3
15 9 10
29. Сложение и вычитание смешанных чисел
ЧТОБЫ СЛОЖИТЬ ( или вычесть) СМЕШАННЫЕ ЧИСЛА,НАДО:
ПРИВЕСТИ ДРОБНЫЕ ЧАСТИ ЭТИХ ЧИСЕЛ К
НАИМЕНЬШЕМУ ОБЩЕМУ ЗНАМЕНАТЕЛЮ;
ОТДЕЛЬНО ВЫПОЛНИТЬ СЛОЖЕНИЕ ( или вычитание)
ЦЕЛЫХ ЧАСТЕЙ И ОТДЕЛЬНО – ДРОБНЫХ ЧАСТЕЙ
ЕСЛИ ПРИ СЛОЖЕНИИ ДРОБНЫХ ЧАСТЕЙ ПОЛУЧИЛАСЬ
НЕПРАВИЛЬНАЯ ДРОБЬ, ВЫДЕЛИТЬ ЦЕЛУЮ ЧАСТЬ ИЗ
ЭТОЙ ДРОБИ И ПРИБАВИТЬ ЕЕ К ПОЛУЧЕННОЙ ЦЕЛОЙ
ЧАСТИ.
9.9.17
30. Сложение и вычитание смешанных чисел
• ЕСЛИ ДРОБНАЯ ЧАСТЬ УМЕНЬШАЕМОГО МЕНЬШЕДРОБНОЙ ЧАСТИ ВЫЧИТАЕМОГО, ТО НАДО ПРЕВРАТИТЬ
ДРОБНУЮ ЧАСТЬ УМЕНЬШАЕМОГО В НЕПРАВИЛЬНУЮ
ДРОБЬ, УМЕНЬШИВ НА ЕДИНИЦУ ЦЕЛУЮ ЧАСТЬ
Например (решаем вместе):
3
1
1). 16 19
8
4
5
3
2). 5 3
6
4
9.9.17
7
1
3). 5 2
9
6
4
5
4). 3 1
9
6
31. Работаем по учебнику
стр.9.9.17
№
32. Умножение дробей
Чтобы умножить дробь на дробь, надочислитель первой дроби умножить на числитель
второй дроби; знаменатель первой дроби
умножить на знаменатель второй дроби.
Т.е.
а с a c
в d в d
9.9.17
33. Умножение дробей
Для дробей, как и для натуральных чисел,выполняются свойства умножения:
( стр. 65 учебника )
9.9.17
34. Обратим внимание
41 1555
9 3 28 7 21
Обратим внимание
При умножении дробей не всегда надо
спешить вычислить произведение числителей и
знаменателей, поскольку удобнее сначала
выполнить сокращение (если это возможно).
Например
4 15 4 15
?
9 28 9 28
1
5
лучше сначала сократить :
4 15
5
9 3 28 7
9.9.17
21
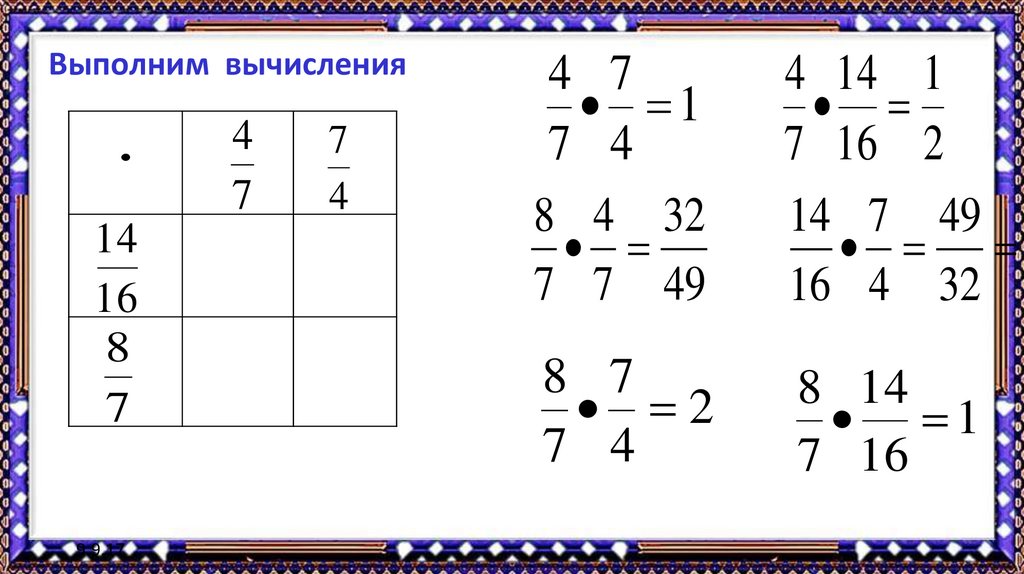
35. Выполним вычисления
.14
16
8
7
9.9.17
4
7
7
4
4 7
1
7 4
8 4 32
7 7 49
4 14 1
7 16 2
14 7 49
16 4 32
8 7
2
7 4
8 14
1
7 16
36. Взаимно обратные числа
Два числа (дроби), произведениекоторых равно 1, называются
взаимно обратными.
Например
9.9.17
4
9
и
9
4
37. Умножение смешанных чисел
Чтобы умножить смешанные числа надо ихзаписать в виде неправильной дроби, а
затем воспользоваться правилом
умножения дробей.
Например
9.9.17
1 1 7 6 7 6 14
4
2 1
2
5
5
3 5 3 5 3 5
38. Работаем по учебнику
стр.9.9.17
№
39. Деление дробей
Чтобы разделить одну дробь на другую,надо делимое умножить на число,
обратное делителю.
Т.е.
а с a c
:
в d в d
9.9.17
40. Обратим внимание
чтоа в
1:
в а
а
0: 0
в
И на нуль делить нельзя
9.9.17
41. Деление смешанных чисел
Чтобы разделить смешанные числа надоих записать в виде неправильной дроби, а
затем воспользоваться правилом деления
дробей.
Например
9.9.17
3 3 15 10 15 7
21
5
3 :1
2
:
8
8
4 7
4 10
4 7
42. Работаем по учебнику
стр.9.9.17
№
43. Преобразование обыкновенной дроби в десятичную
Чтобы преобразовать обыкновенную дробь вдесятичную, надо числитель дроби
разделить на её знаменатель.
9.9.17
44. Преобразование обыкновенной дроби в десятичную
Чтобы преобразовать несократимуюобыкновенную дробь в десятичную, надо
привести её к одному из знаменателей: 10, 100,
1000 и т.д.
Несократимую обыкновенную дробь можно
преобразовать в десятичную тогда и только
тогда, когда разложение знаменателя дроби на
простые множители содержит только множители
2и5
9.9.17
45. Обратим внимание
При делении натурального числа нанатуральное число можно получить:
- натуральное число
- конечную десятичную дробь
- бесконечную периодическую
десятичную дробь
9.9.17
46. Работаем по учебнику
стр.9.9.17
№
47.
9.9.1748. Источники ресурса
Шаблон создан на основе клипарта рамкиhttp://abload.de/img/gzdeforumdnyas-png-ce32u4u.png
И возможностей программы Microsoft PowerPoint 2016
Шаблон презентации подготовила учитель русского языка и литературы Тихонова Надежда
Андреевна, г. Костанай
А.Г. Мерзляк и др., Математика: 6 класс: учебник для учащихся общеобразовательных
организаций/ - 2-е изд., перераб. – М. : Вентана-Граф,2016.
http://u.900igr.net:10/datai/matematika/Naimenshee-obschee-kratnoe/0018-009-18.png
https://data3.proshkolu.ru/content/media/pic/icon/3000000/2824000/2823051-1a9d966c.gif
https://data3.proshkolu.ru/content/media/pic/icon/3000000/2824000/2823051-1a9d966c.gif











































 mathematics
mathematics








