Дробь – число, состоящее из частей единицы

1. Повторим

«Дробь – число, состоящее
из частей единицы».
9.9.17

2. Повторим

Знаменатель дроби показывает,
на сколько равных частей разделено целое.
Числитель показывает, сколько частей взяли.
9.9.17

3. Повторим

a
a :b
b
Дроби бывают: правильными и
неправильными
9.9.17

4. Основное свойство дроби

ЕСЛИ ЧИСЛИТЕЛЬ И ЗНАМЕНАТЕЛЬ ДРОБИ
УМНОЖИТЬ ИЛИ РАЗДЕЛИТЬ НА ОДНО И ТО
ЖЕ НАТУРАЛЬНОЕ ЧИСЛО, ТО ПОЛУЧИТСЯ
РАВНАЯ ЕЙ ДРОБЬ.
×
1 2 8 40
2 4 16 80
:
9.9.17

5. Сокращение дробей

ДЕЛЕНИЕ ЧИСЛИТЕЛЯ И ЗНАМЕНАТЕЛЯ НА ИХ ОБЩИЙ
ДЕЛИТЕЛЬ, ОТЛИЧНЫЙ ОТ ЕДИНИЦЫ, НАЗЫВАЮТ
СОКРАЩЕНИЕМ ДРОБИ.
2 2:2 1
6 6:2 3
12
25
9.9.17
35 35 : 7 5
14 14 : 7 2
- несократимая дробь

6. Сокращение дробей

• НАИБОЛЬШЕЕ ЧИСЛО, НА КОТОРОЕ МОЖНО СОКРАТИТЬ
ДРОБЬ, - ЭТО НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ ЕЁ
ЧИСЛИТЕЛЯ И ЗНАМЕНАТЕЛЯ.
• У НЕСОКРАТИМОЙ ДРОБИ ЧИСЛИТЕЛЬ И ЗНАМЕНАТЕЛЬ
– ЭТО ВЗАИМНО ПРОСТЫЕ ЧИСЛА
• ПРИ СОКРАЩЕНИИ ДРОБЕЙ ИСПОЛЬЗУЮТ ПРИЗНАКИ
ДЕЛИМОСТИ 150
50 10
2
225
9.9.17
75
15
3

7. Сокращение дробей

• ПРИ СОКРАЩЕНИИ ДРОБЕЙ ТАК ЖЕ ИСПОЛЬЗУЮТ
РАЗЛОЖЕНИЕ ЧИСЛА НА ПРОСТЫЕ МНОЖИТЕЛИ
3
5 3 3 3
135 5 27
180 18 10 2 3 3 2 5 4
9.9.17

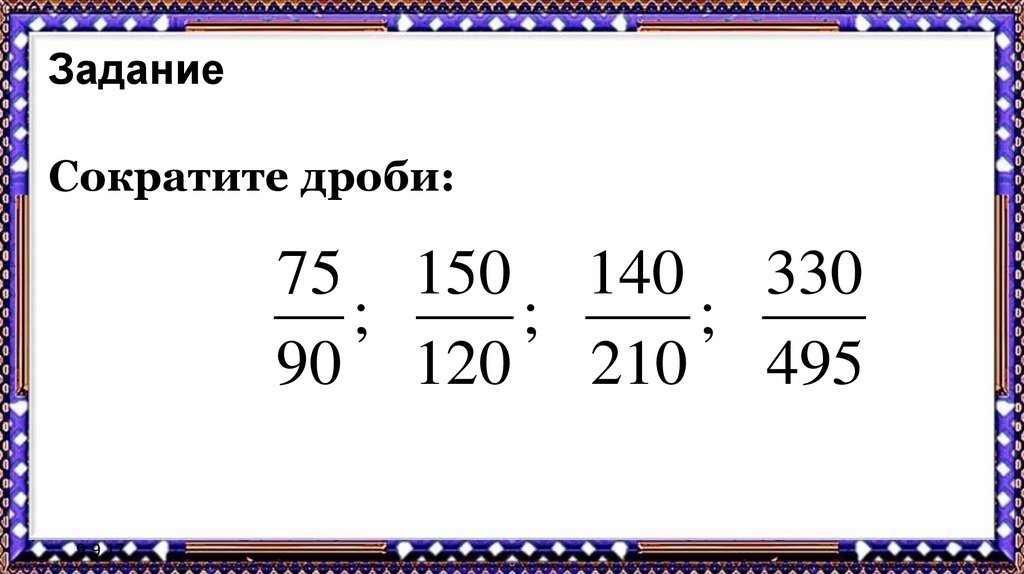
8. Задание

Сократите дроби:
75 150 140 330
;
;
;
90 120 210 495
9.9.17

9. Умножение дробей

Чтобы умножить дробь на дробь, надо
числитель первой дроби умножить на числитель
второй дроби; знаменатель первой дроби
умножить на знаменатель второй дроби.
Т.е.
а с a c
в d в d
9.9.17

10. Умножение дробей

Для дробей, как и для натуральных чисел,
выполняются свойства умножения:
( стр. 68 учебника )
9.9.17

11. Обратим внимание

41 155
5
9 3 28 7 21
Обратим внимание
При умножении дробей не всегда надо
спешить вычислить произведение числителей и
знаменателей, поскольку удобнее сначала
выполнить сокращение (если это возможно).
Например
4 15 4 15
?
9 28 9 28
1
5
лучше сначала сократить :
4 15
5
9 3 28 7
9.9.17
21

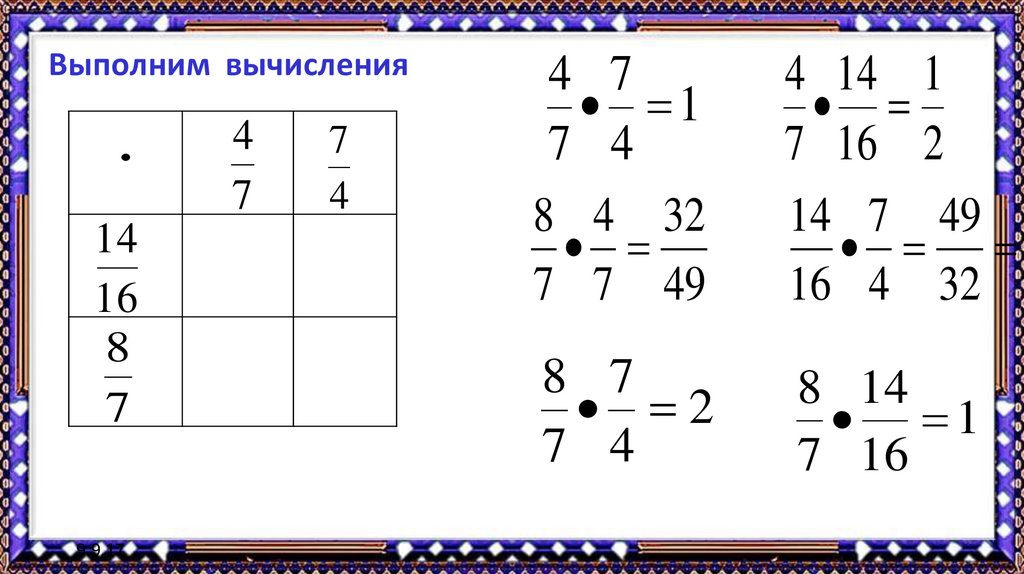
12. Выполним вычисления

.
14
16
8
7
9.9.17
4
7
7
4
4 7
1
7 4
8 4 32
7 7 49
4 14 1
7 16 2
14 7 49
16 4 32
8 7
2
7 4
8 14
1
7 16

13. Умножение смешанных чисел

Чтобы умножить смешанные числа надо их
записать в виде неправильной дроби, а
затем воспользоваться правилом
умножения дробей.
Например
9.9.17
1 1 7 6 7 6 14
4
2 1
2
5
5
3 5 3 5 3 5

14. Преобразование обыкновенной дроби в десятичную

Чтобы преобразовать обыкновенную дробь в
десятичную, надо числитель дроби
разделить на её знаменатель.
9.9.17

15. Преобразование обыкновенной дроби в десятичную

Чтобы преобразовать несократимую
обыкновенную дробь в десятичную, надо
привести её к одному из знаменателей: 10, 100,
1000 и т.д.
Несократимую обыкновенную дробь можно
преобразовать в десятичную тогда и только
тогда, когда разложение знаменателя дроби на
простые множители содержит только множители
2и5
9.9.17

16. Обратим внимание

При делении натурального числа на
натуральное число можно получить:
- натуральное число
- конечную десятичную дробь
- бесконечную периодическую
десятичную дробь
9.9.17