Similar presentations:
Действия с обыкновенными дробями
1. Обобщающий урок математики в 6 классе по теме: «Действия с обыкновенными дробями»
2. Цели и задачи урока
• повторить и закрепить изученные по темеправила
• повторить методы решения задач по данной
теме
• закрепить полученные навыки действий с
обыкновенными дробями
• повторить некоторые исторические сведения
о дробях
3. Некоторые исторические сведения о дробях
1.Как и когда появились первыепредставления людей о дробях?
Первые представления о дробях возникли в процессе
измерения (длин, площадей, веса и т.д.).
Уже в Древнем Вавилоне и Древнем Риме люди
широко использовали дроби. Тогда использовались
шестидесятеричные (т.е. со знаменателем 60) и
двенадцатеричные (т.е. со знаменателем 12) дроби.
4.
2. Когда и где стали использоватьсовременные правила действий с
дробями?
Правила действий с дробями в том виде, что сейчас
используем и мы были известны уже в 8 веке
нашей эры и широко использовались греками и
индийцами. А в Западную Европу дроби были
перенесены лишь в 13 веке, а десятичные дроби
еще позднее - только в 16-17 веках.
5. Сложение и вычитание дробей с разными знаменателями
Чтобы сравнить ( сложить или вычесть )дроби с разными знаменателями, надо:
1.Привести данные дроби к общему
знаменателю,
2.Сравнить, ( сложить или вычесть )
полученные дроби
6.
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙКак привести дроби к общему знаменателю?
1.Знаменатели - взаимнопростые числа
5
2.Знаменатель одной дроби делится на
знаменатель другой дроби
3
2
3
3
3
5
10
15
9
15
1
15
3
8
Общим знаменателем является
произведение знаменателей
5
24
9
24
5
24
14
24
Общим знаменателем является
больший знаменатель
3. Общим знаменателем является наименьшее общее кратное
5
4
5
12
3
15
25
60
12
60
12 = 2 · 2 · 3
15 = 3 · 5
37
60
НОК(12,15) = 2 · 2 · 3 · 5 = 60
Наименьшее общее кратное
натуральных чисел это
наименьшее натуральное число,
которое является кратным обоих
этих чисел
10
15
7. Устный счет
1.Сравнить дроби:а)
7
9
7
9
1
3
б) 5
8
5
6
в)
3
9
1
8
1
6
9
116
9
8
16
15
7
16
1
16
8
1 - 15
7
15
1
15
8. Устный счет
Дана дробь11
41
.
Какое число нужно прибавить
к числителю и знаменателю этой дроби,
чтобы она обратилась в
3
8
6
16
9
24
12
32
3
8
?
15
40
Ответ: нужно прибавить число 7.
18
48
9. Умножение дробей
Чтобы умножить дробь на натуральноечисло, надо ее числитель умножить на это
число, а знаменатель оставить без
изменения.
3
5
· 4
3
5
·
4
12
5
2
2
5
10. Умножение дробей
Чтобы умножить дробь на дробь,надо:1. Найти произведение числителей и
произведение знаменателей этих
дробей,
2. Первое произведение записать
числителем, а второе- знаменателем.
2
3
2
5
·
·
5
7
5
6
2
3
2
5
·
·
·
·
5
7
5
6
10
21
1
2
5
1
·
·
5
6
1
3
1
1
·
·
1
3
1
3
11. Умножение дробей
Чтобы выполнить умножение смешанныхчисел, надо записать их в виде
неправильных дробей, а затем
воспользоваться правилом умножения
дробей.
3
44
8
9
5
·119
3
·124
19
4
·
·
8
9
·
·
24
19
27
24
1
19
4
1
1
8
9
1
·
·
·
·
6
24
19 1
3
27
24 3
1
1
·
·
6
1
6
1
6
1
1
·
·
3
3
1
1
1
12.
УМНОЖЕНИЕ ДРОБЕЙРаспределительное свойство
умножение относительно
сложения и вычитания
(а+в)с=ав+ас (а-в)с=ас-ас
7· 4
2
7 =7
9 ·5
2
9
·
·
1
7
36
7
· (4
2
7
7
9
1
7
8
·5
2
9
1
·
·
)=7·
= (9
4
36
7
2
1
4
8
·
·
4
7
7
9
7·
2
7
)·5
1
7
8
7
=28+2=30
=
= 1
2
9
1
7
·5
1
7
=
13. Деление дробей
Чтобы разделить одну дробь на другую, надоделимое умножить на число, обратное делителю.
Какие числа называются
Два числа, произведение
которых равно 1, называют
взаимно обратными.
взаимно обратными?
3
:
5
12
5:
2
5
4
3
4
=
3 12
16 · 5
5
2
=
3
16
5
1
= 5· =
: 3 194 ·· 13 =
=
3
16
· 12 3 · 12
3 · 3
· 5 =4 16 · 5 = 4 · 5
· 5 25
1
· 2 = 2 = 122
19 · 1
19
7
1
4 · 3 = 12 =
12
=
9
20
14.
Вычислить значение выражения:1
2
(2
1)
2)
3)
1
2
+1
5
6
1
6
2
3
+1
23
:
5
1
3
)
1
6
:
1
3
3
5
= 22
7
7
=
17
5
6
23 6
· 1
6
3
7
3
7
23
5
3
7
= 17
4
7
4
7
15. Нахождение дроби от числа
Чтобы найти дробь от числа,надо число умножить на эту дробь
а) Найти четыре седьмых от 28 .
4
7
28 ·
4
28
1
·
·
4
7
=1
4
1
28
1
·
·
4
7
·
·
4
1
=
=
16
Ответ: четыре седьмых от 28 равны 16.
16.
б) Найти 35% от 70Нахождение
дроби от числа
35%=0,35
70 · 0,35= 24,50
Ответ: 35% от 70 равны 24,5
в) Найти 0,8 от 900
900 · 0,8 = 720
Ответ: 0,8 от 900 равны 720
17. Нахождение числа по его дроби
Чтобы найти число по данному значению его дроби,надо это значение разделить на дробь.
а)Найти число, 0,37 которого равны 14,8.
14,8:0,37=1480:37=40
Ответ: 40 - это число,
0,37 которого равны 14,7.
18.
Нахождениячисла по его
дроби
б)Найти число, 63% которого равны 126
126:0,63=12600:63=200
Ответ:число, 63% которого равны 126 - это число 200.
9
в)Найти число, 11 которого равны 27
27 :
9
11
Ответ:
=
27 11
1 ·9
9 от
11
=
33
3
27 · 11
1 · 9 1
=
равны
27
3
1
· 11
33
=
1
·
19.
Задача № 1Соловьев Сережа и Афиногентов Антон
составляют одну четырнадцатую всех учащихся
6В класса. Сколько этом классе девочек, если
известно, что их количество составляет три
седьмых всех учащихся?
2 учащихся - 1
14
всего класса
3
Девочки - ? ,
всего класса
7
20.
2 учащихся - 1всего класса
14
3
Девочки - ? , 7 всего класса
РЕШЕНИЕ
1)
2)
2:
1
14
28 ·
= 28
3
7
(уч.)-всего в классе.
= 12
(уч.)-девочки
ОТВЕТ: Двенадцать девочек учится в 6В классе.
Задача № 1
21.
Задача № 2Туристы на машине проехали 28% всего пути,
поездом
19
27 оставшегося пути, а затем плыли на
теплоходе. Сколько километров туристы проплыли на
теплоходе, если на машине они проехали 126 км?
Машина - 126 км., 28% всего пути
Поезд
-
? км., 19
27
Теплоход - ? км.
оставшегося пути
22.
Машина - 126 км., 28% всего пути19
Поезд
- ? км.,
оставшегося пути
27
Теплоход - ? км.
РЕШЕНИЕ
1) 126:0,28=12600:28=450 (км.) - весь путь
2) 450-126=324 (км.) - оставшийся путь
3) 324
· 19
27
228 (км.) - поездом
4) 324-228=96 (км.) - теплоходом.
Ответ: 96 километров туристы проплыли на теплоходе.
23. Решение уравнений
115
3
х
а) 2
4
3
1
х
2
4
15
1
3
х
1
4
12
1
3
Х= 1 12
4
4
Х= 1 9
:
59
60
59
60
2
1
1
15
1
1 12
:
Ответ:
1
2
3
4
13
12
1
4
60
59
60
5
1 60
59
60
64
60
13
9
4
9
59
60
4
9
·
1
1 12
4
3
24.
б)5
7
у
2
7
у
у=
2
9
у=
у
2
9
2
9
2
7
:
2
9
7
9
Ответ:
Решение
уравнений
7
9
:
2
7
=
1
2
9
·
·
7
2
=1
7
9
25.
Задача №3Бассейн наполняется водой через первую трубу
за 5 часов, а через вторую за 7 часов. Какую часть
бассейна останется заполнить, если первая труба
работала 2 часа, а вторая - 3 часа?
Сколько понадобится времени, чтобы заполнить
оставшуюся часть бассейна, если обе трубы
будут работать одновременно?
1 труба
2 труба
26.
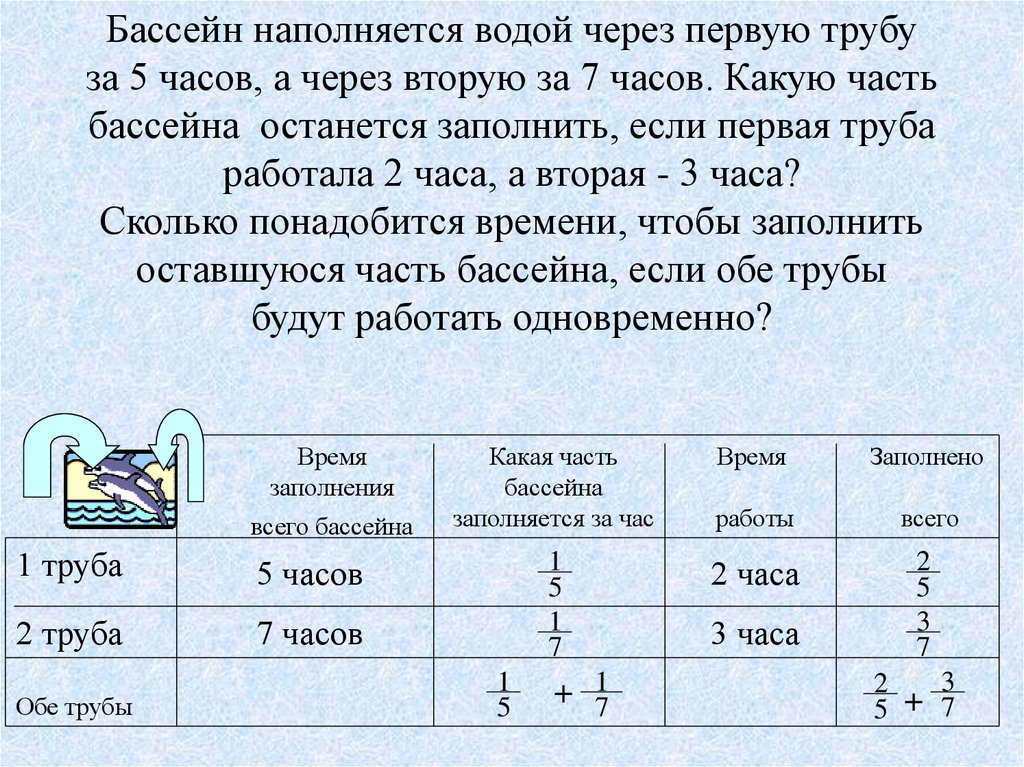
Бассейн наполняется водой через первую трубуза 5 часов, а через вторую за 7 часов. Какую часть
бассейна останется заполнить, если первая труба
работала 2 часа, а вторая - 3 часа?
Сколько понадобится времени, чтобы заполнить
оставшуюся часть бассейна, если обе трубы
будут работать одновременно?
Время
заполнения
всего бассейна
1 труба
5 часов
2 труба
7 часов
Обе трубы
Какая часть
бассейна
заполняется за час
1
5
1
7
1
5
+ 17
Время
Заполнено
работы
всего
2 часа
2
5
3
7
3 часа
3
2
+
7
5
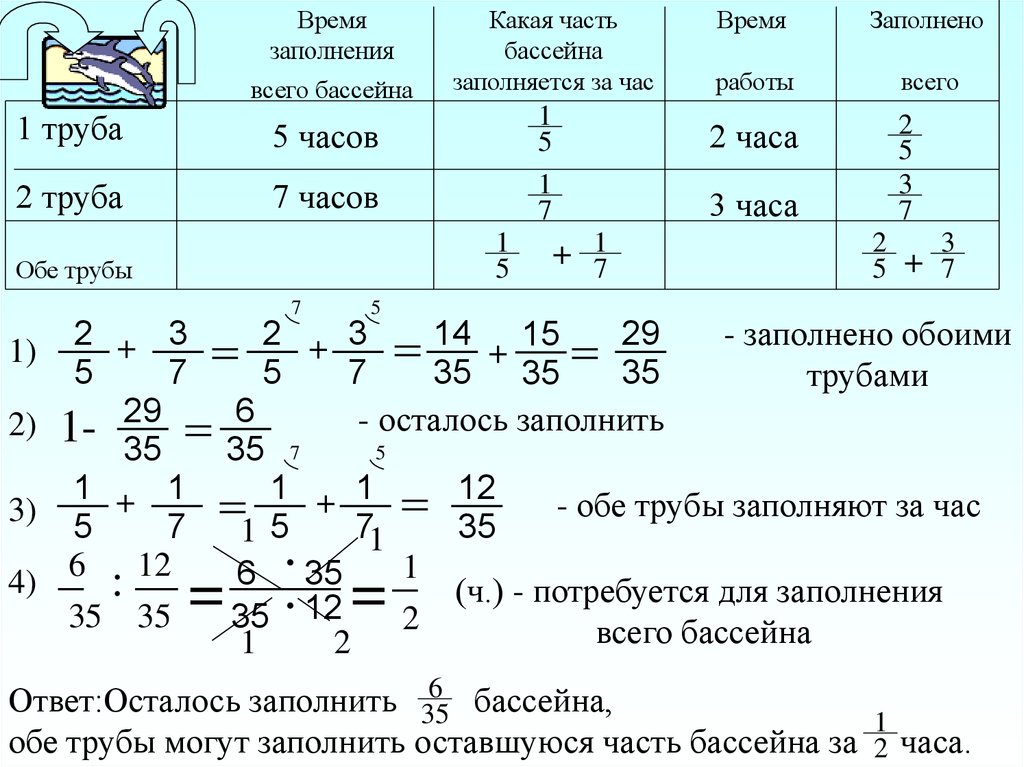
27.
Времязаполнения
всего бассейна
1 труба
5 часов
2 труба
7 часов
7
2
5
2)
1-
1
5
1
7
1
5
Обе трубы
1)
Какая часть
бассейна
заполняется за час
3
7
2
5
29
35
1
1
3)
5
7
4) 6 : 12
35 35
6
35
=
Заполнено
работы
всего
2 часа
2
5
3
7
3 часа
+ 17
5
3
14 15
29
7
35 35
35
- осталось заполнить
7
Время
2
3
5 + 7
- заполнено обоими
трубами
5
1
1
71
15
1
6 · 35
35 · 12
2
1
2
=
12
35
- обе трубы заполняют за час
(ч.) - потребуется для заполнения
всего бассейна
6 бассейна,
Ответ:Осталось заполнить 35
1
обе трубы могут заполнить оставшуюся часть бассейна за 2 часа.
28. Домашняя работа
Сравнить12
23
и
13
24
№ 816
№ 803 а)
СПАСИБО ЗА УРОК!!!
.













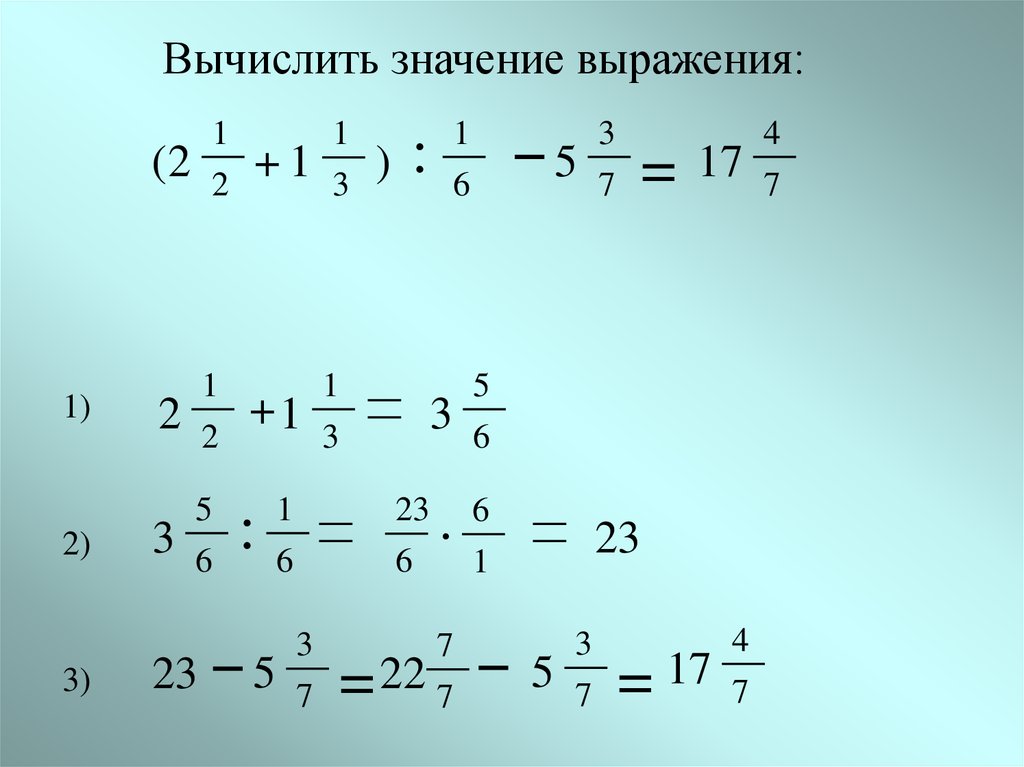











 mathematics
mathematics








