Прямая

1.

ПРЯМАЯ

2.

Классификация прямых
1. Прямые общего положения – это прямые, непараллельные и
неперпендикулярные ни одной из плоскостей проекций.
2. Прямые частного положения:
• Уровня – параллельные одной из плоскостей проекций и не
перпендикулярные двум другим;
• Проецирующие – перпендикулярные к одной плоскости
проекций и параллельные двум другим.

3.

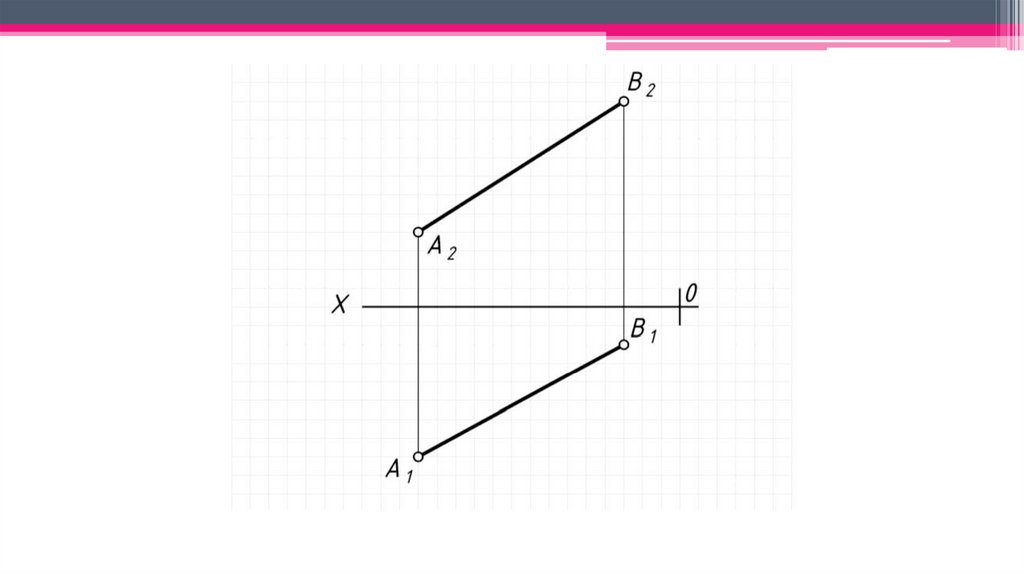
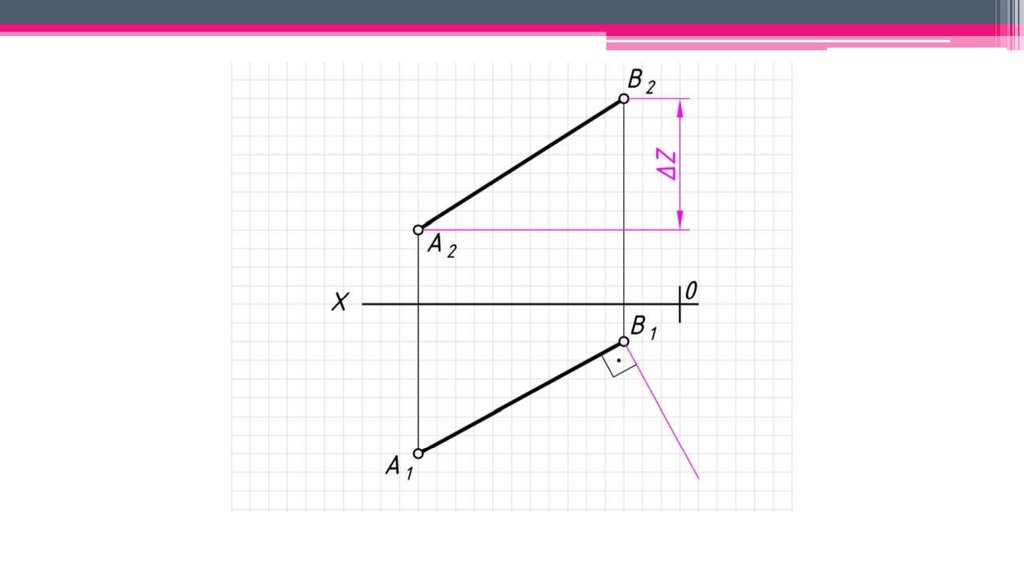
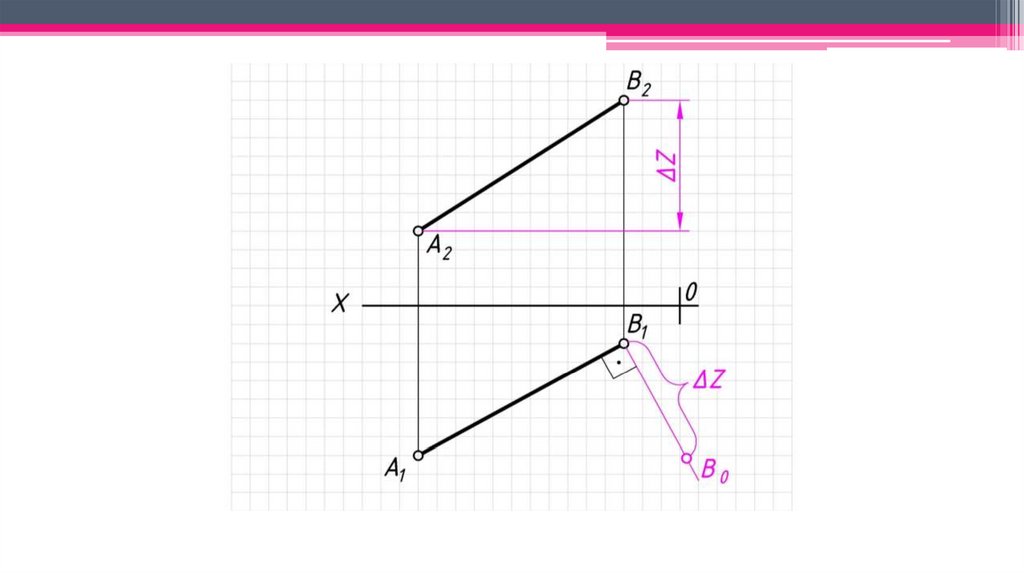
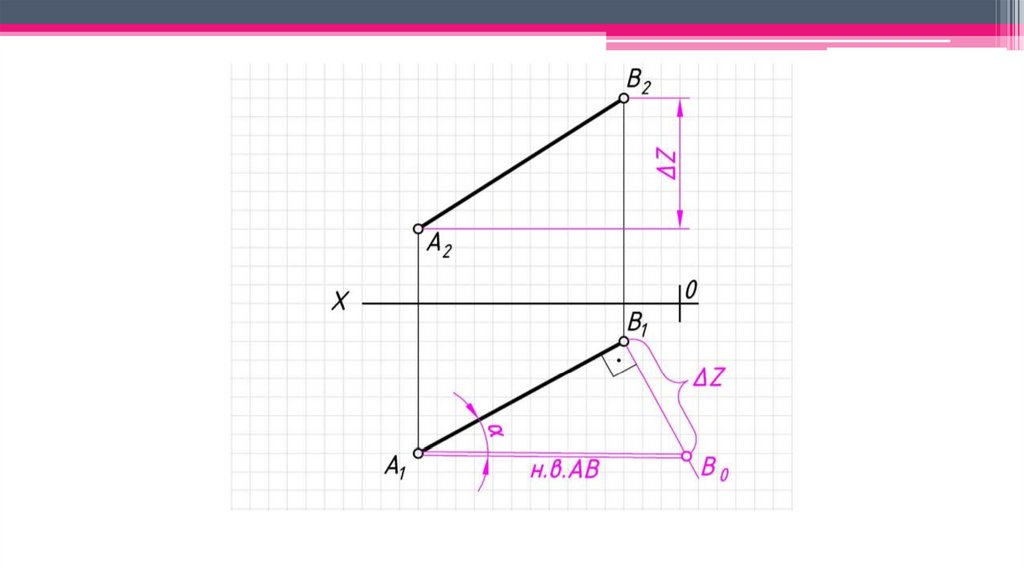
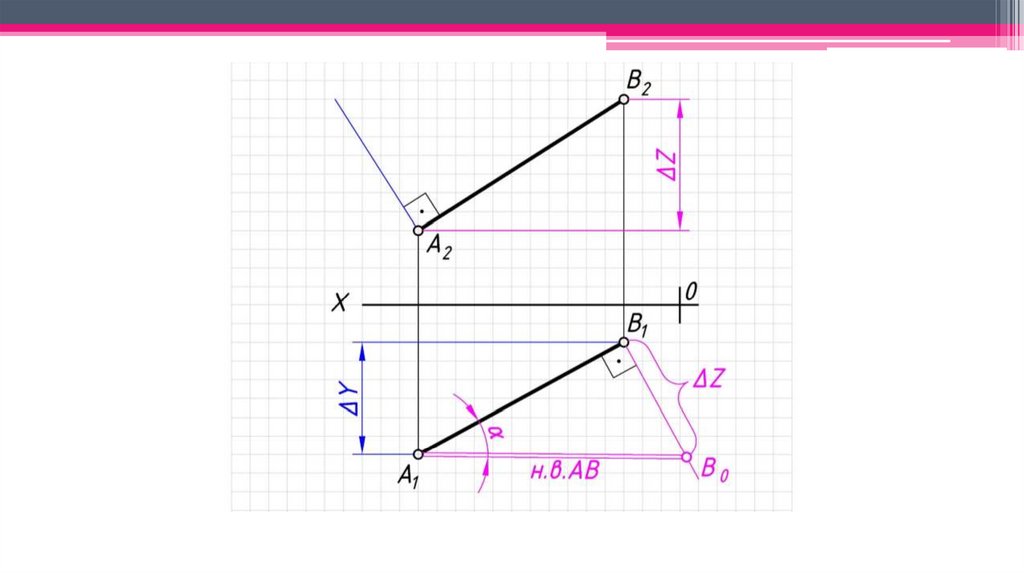
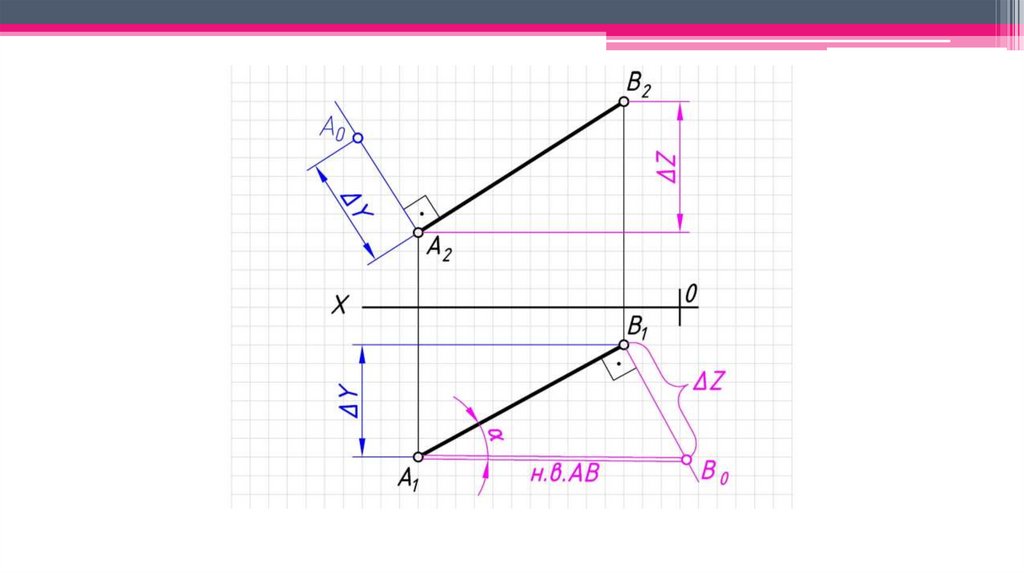
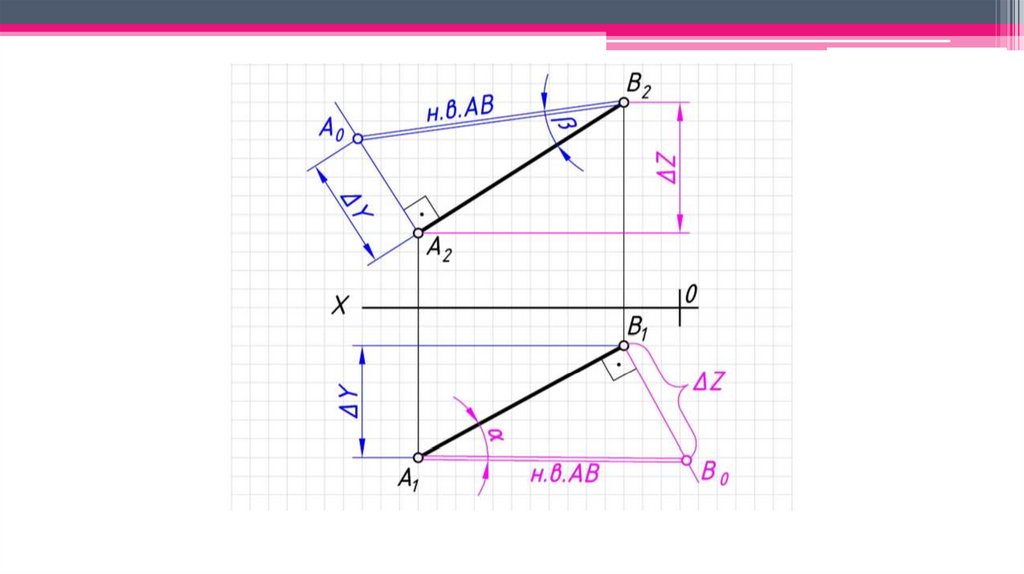
Позиционно-метрические свойства прямой:
1. Натуральная величина прямой – определяется способом прямоугольного
треугольника.
2. Угол наклона отрезка прямой к соответствующей плоскости
проекций является угол между его проекцией на данную плоскость и
натуральной величиной рассматриваемого отрезка.

4.

5.

6.

7.

8.

9.

10.

11.

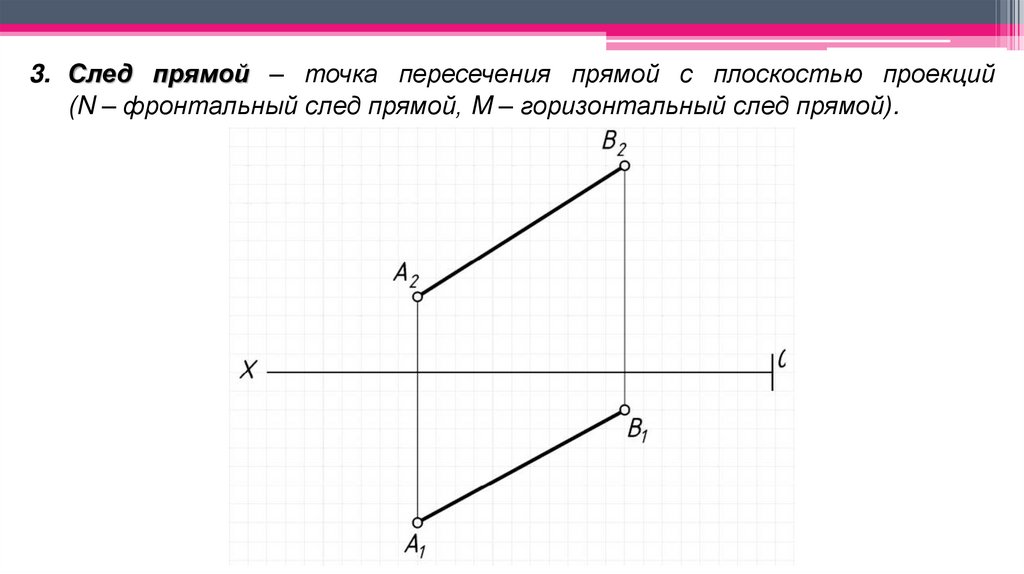
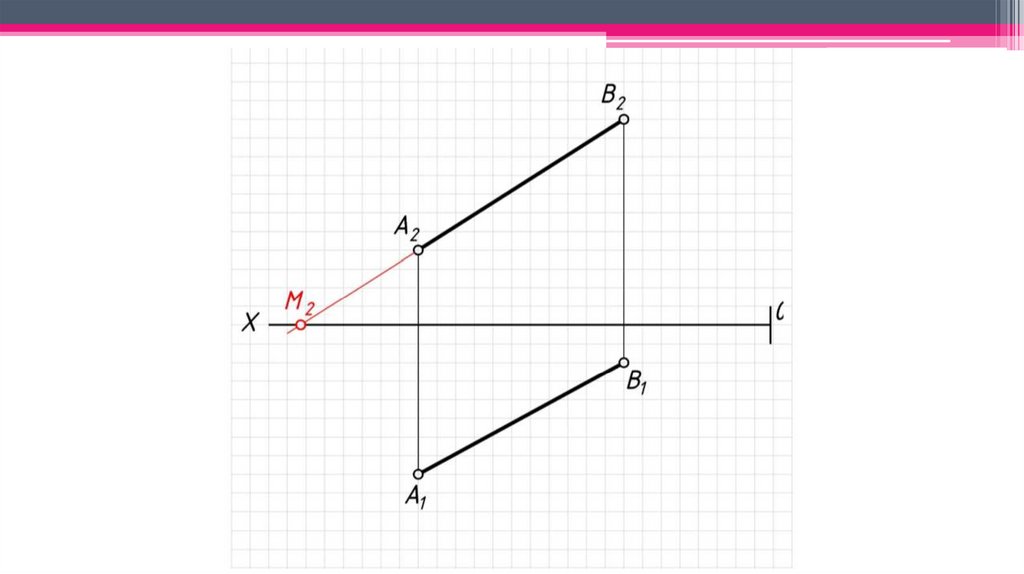
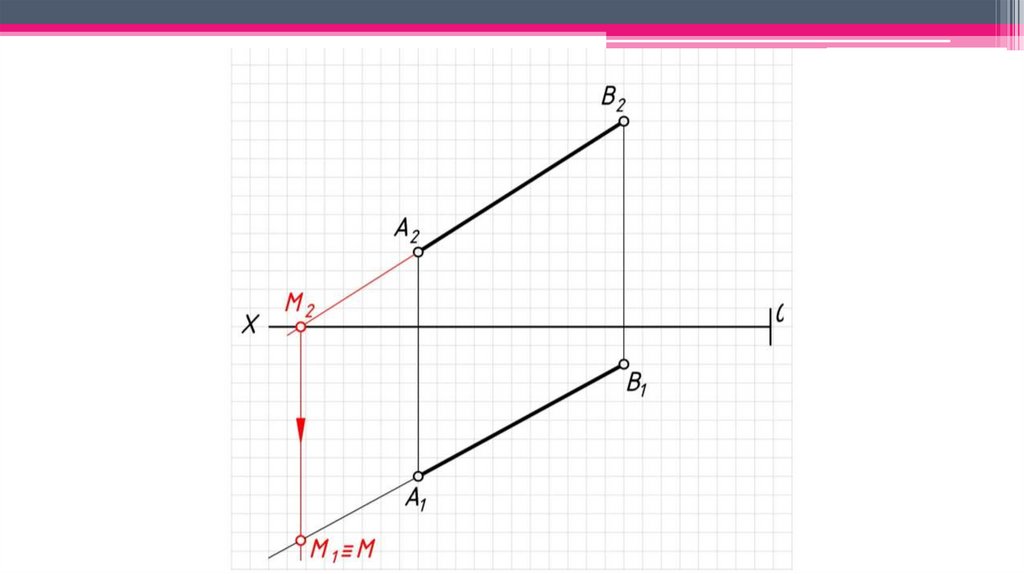
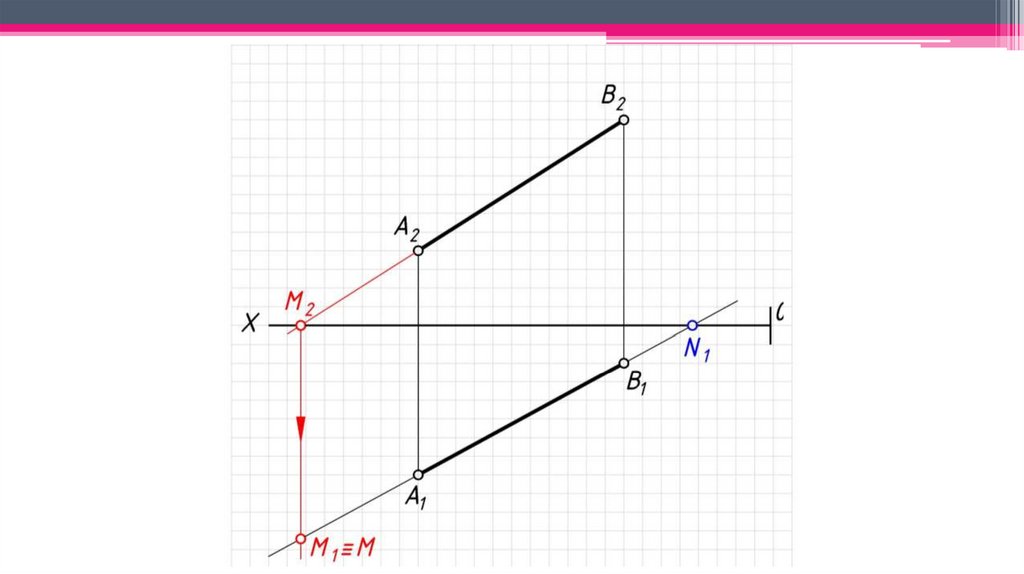
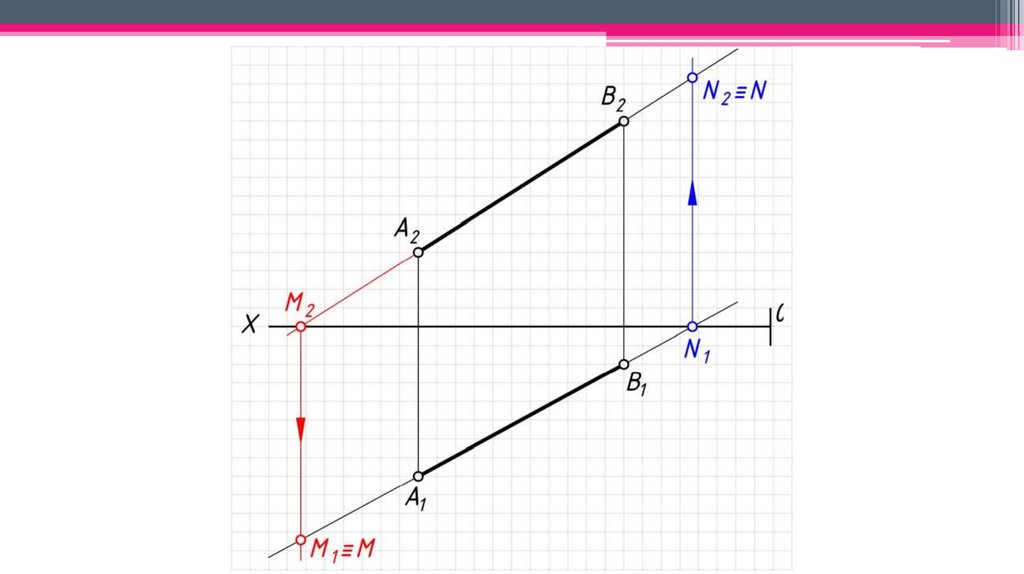
3. След прямой – точка пересечения прямой с плоскостью проекций
(N – фронтальный след прямой, M – горизонтальный след прямой).

12.

13.

14.

15.

16.

4. Принадлежность точки прямой.
Теорема: Если в пространстве точка принадлежит прямой, то на чертеже
одноименные проекции точки принадлежат одноименным проекциям прямой.
Теорема: Если в пространстве точка делит отрезок прямой в каком-то
отношении, то на чертеже проекции этой точки делят одноименные
проекции отрезка в том же отношении.

17.

4. Принадлежность точки прямой.
Теорема: Если в пространстве точка принадлежит прямой, то на чертеже
одноименные проекции точки принадлежат одноименным проекциям прямой.
Теорема: Если в пространстве точка делит отрезок прямой в каком-то
отношении, то на чертеже проекции этой точки делят одноименные
проекции отрезка в том же отношении.

18.

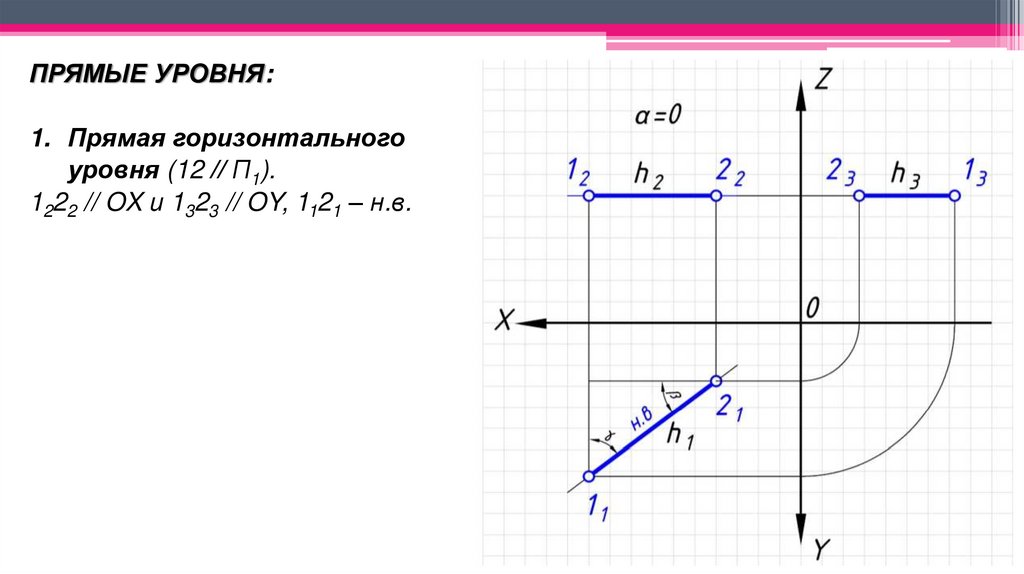
ПРЯМЫЕ УРОВНЯ:
1. Прямая горизонтального
уровня (12 // П1).
1222 // OX и 1323 // OY, 1121 – н.в.

19.

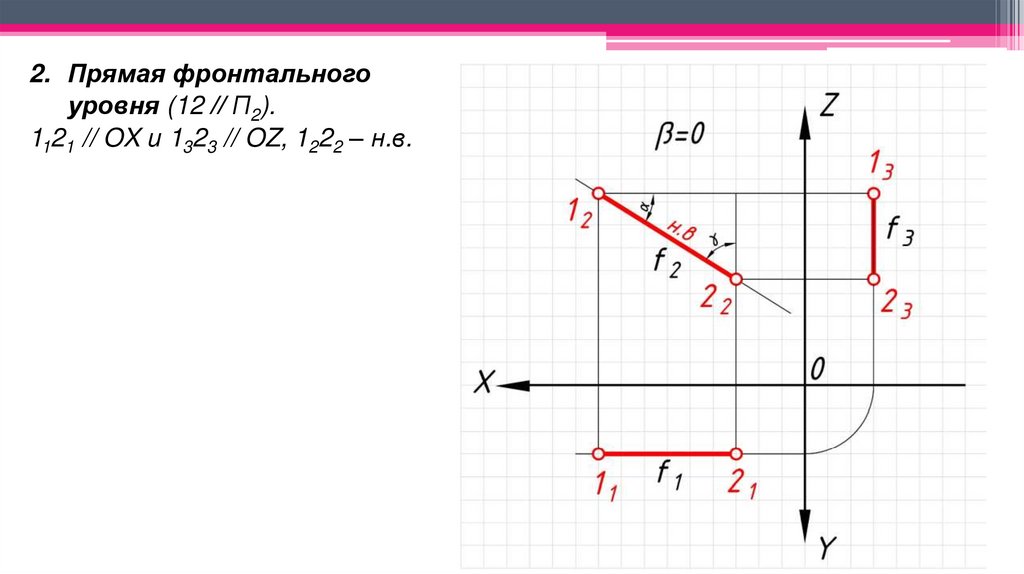
2. Прямая фронтального
уровня (12 // П2).
1121 // OX и 1323 // OZ, 1222 – н.в.

20.

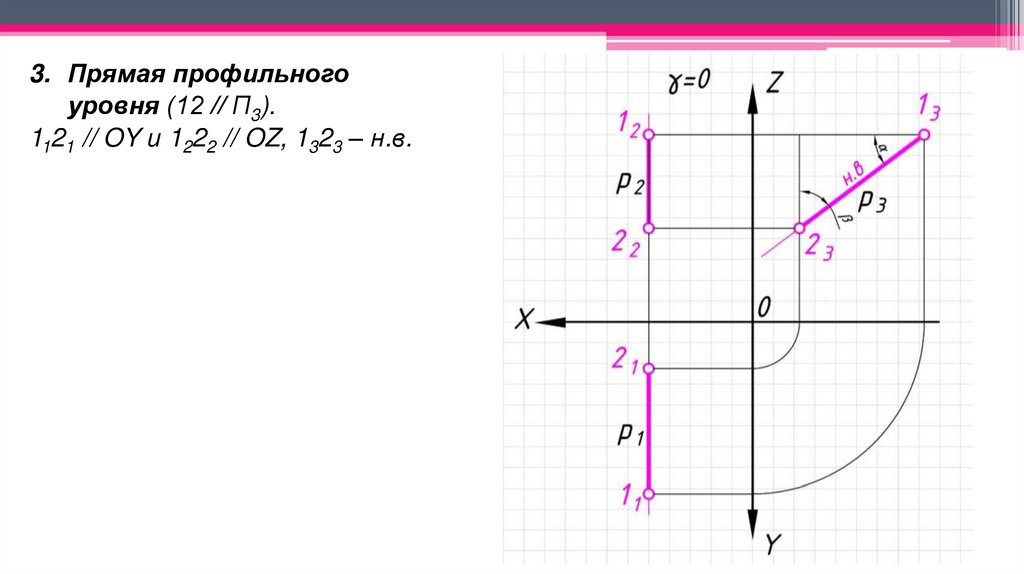
3. Прямая профильного
уровня (12 // П3).
1121 // OY и 1222 // OZ, 1323 – н.в.

21.

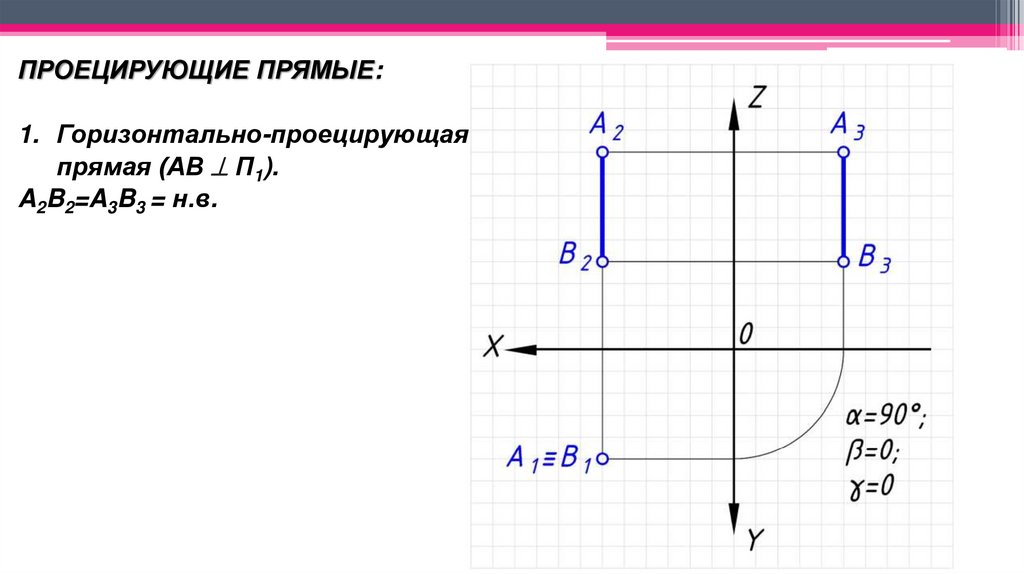
ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ:
1. Горизонтально-проецирующая
прямая (АВ П1).
A2B2=A3B3 = н.в.

22.

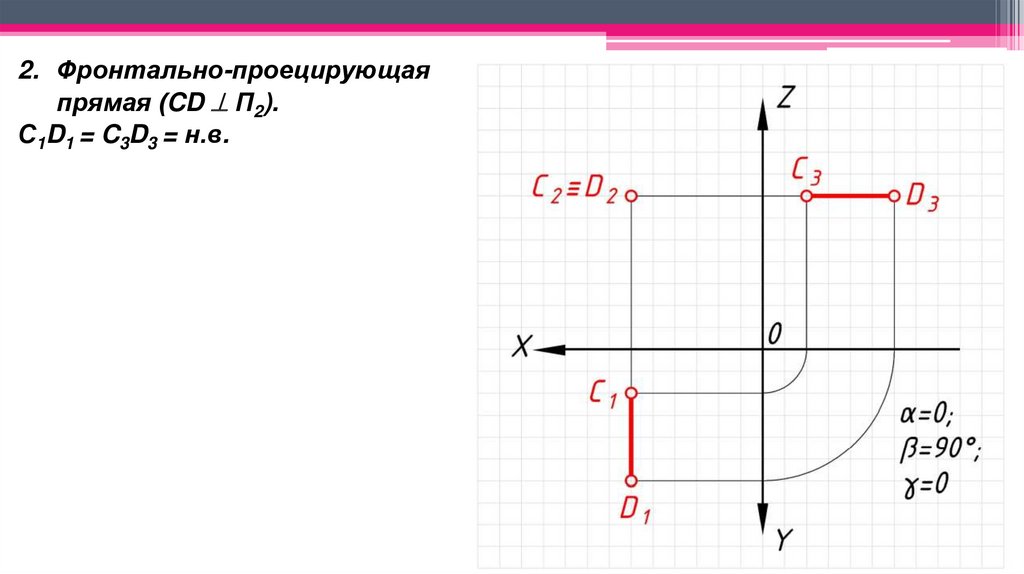
2. Фронтально-проецирующая
прямая (CD П2).
С1D1 = C3D3 = н.в.

23.

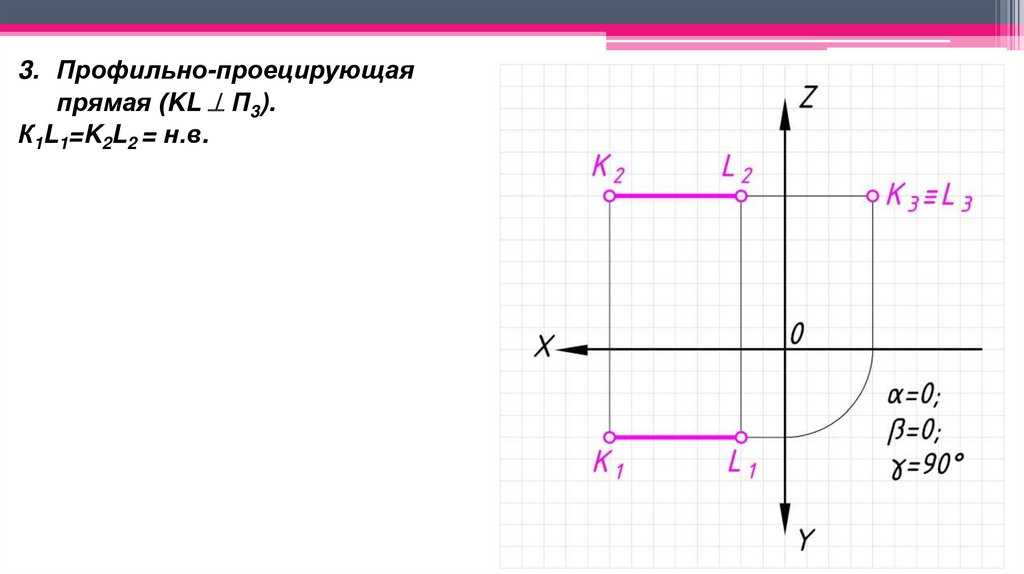
3. Профильно-проецирующая
прямая (KL П3).
К1L1=K2L2 = н.в.

24.

ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ
Параллельные прямые – прямые, принадлежащие одной плоскости и не
имеющие общей точки пересечения.

25.

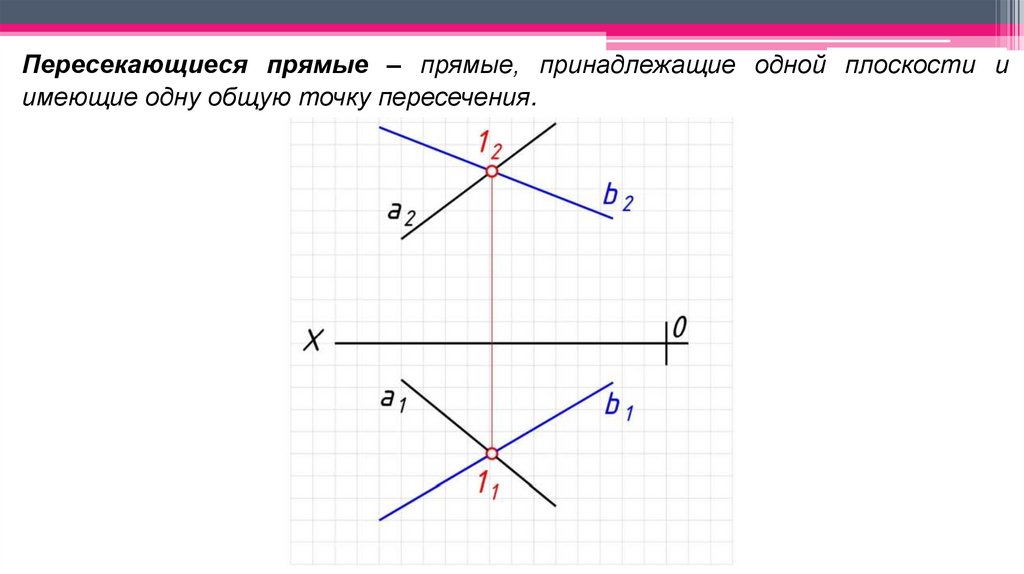
Пересекающиеся прямые – прямые, принадлежащие одной плоскости и
имеющие одну общую точку пересечения.

26.

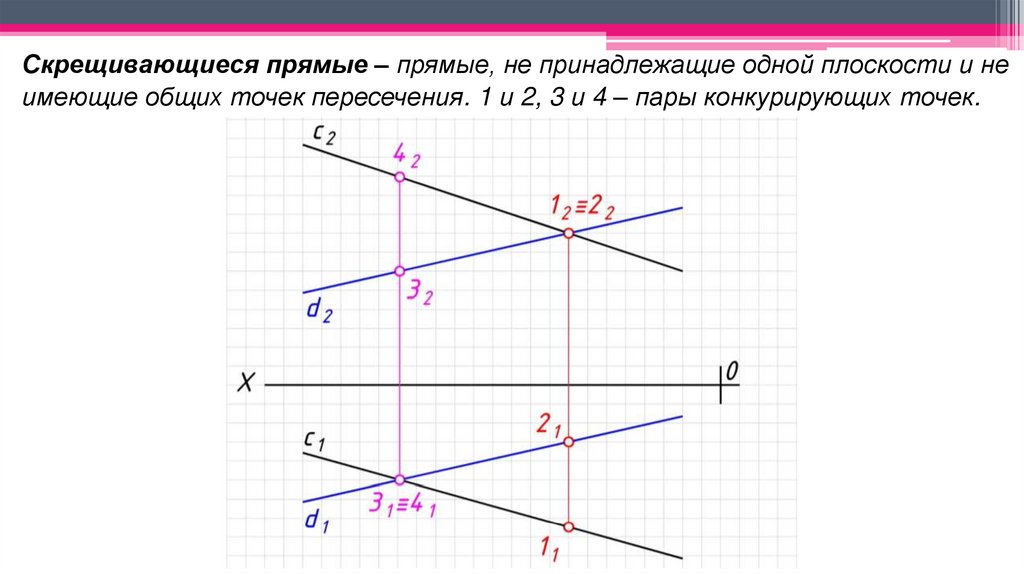
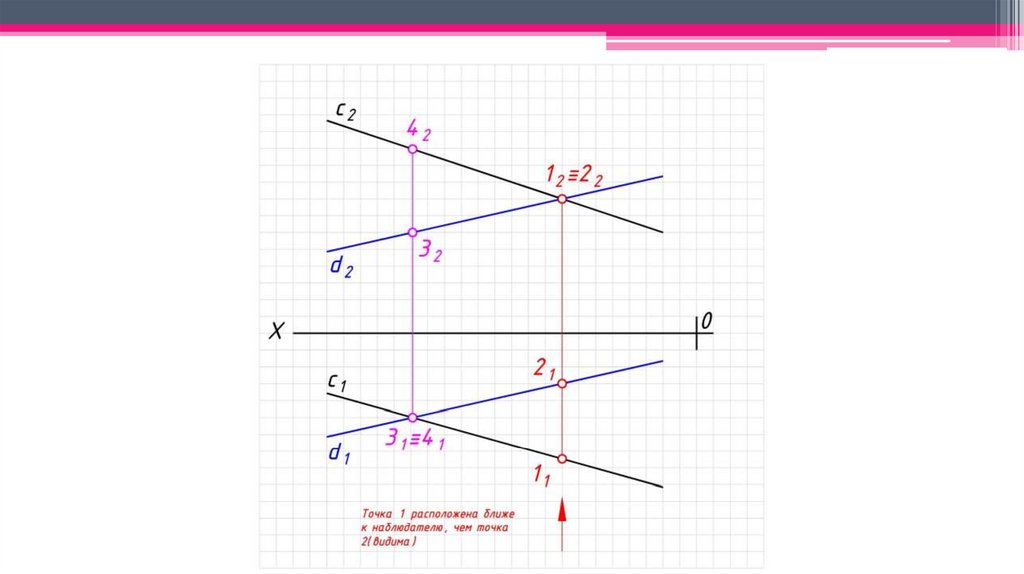
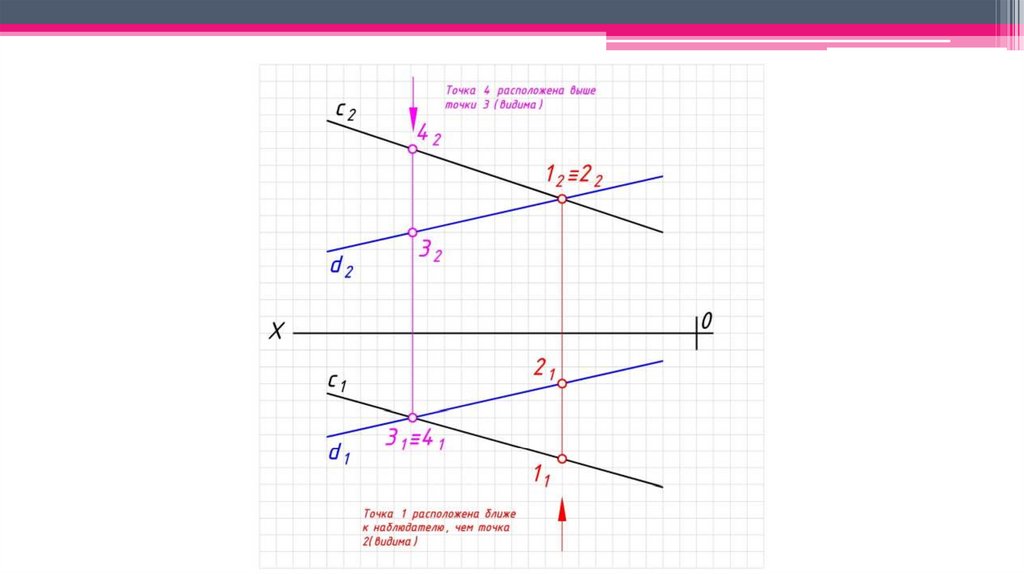
Скрещивающиеся прямые – прямые, не принадлежащие одной плоскости и не
имеющие общих точек пересечения. 1 и 2, 3 и 4 – пары конкурирующих точек.