Similar presentations:
Конструктивная геометрия. Прямая линия. Лекция 4
1.
Дальневосточный государственный университетпутей сообщения
Кафедра «Вычислительная техника и компьютерная графика»
Company Logo
2.
План лекцииПрямая линия и ее задание
Комплексный чертеж прямой линии
Принадлежность точки прямой линии
Положения прямой относительно
плоскостей проекций
Взаимные положения точки и прямой линии
Взаимные положения двух прямых
1
3.
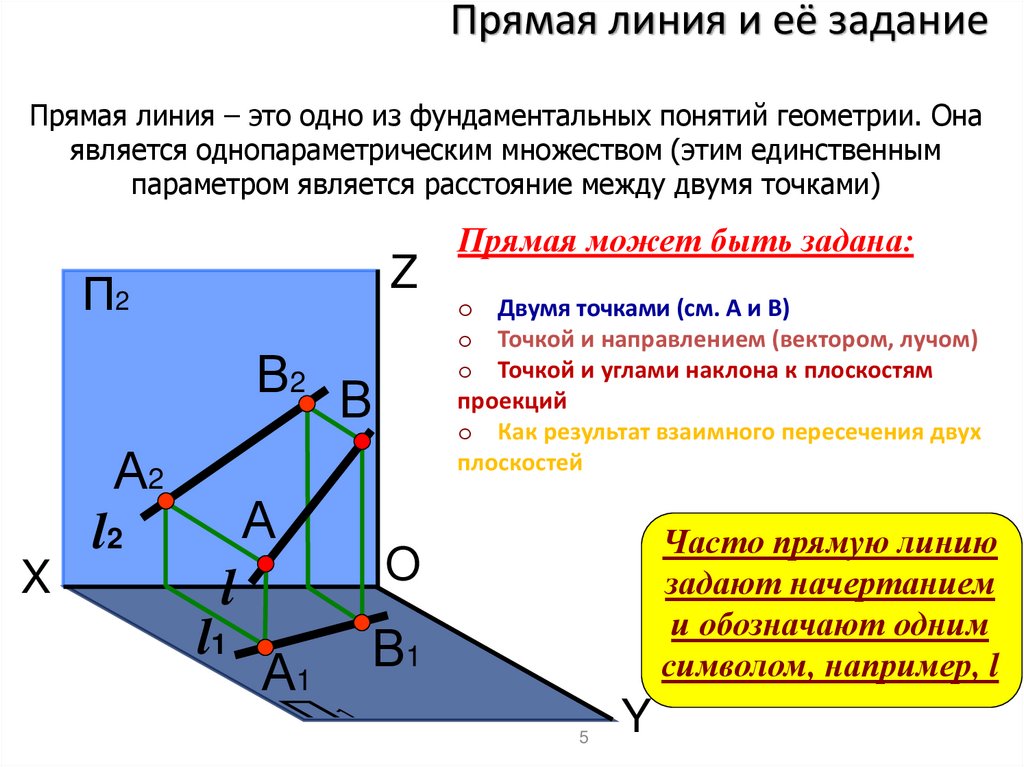
Прямая линия и её заданиеПрямая линия – это одно из фундаментальных понятий геометрии. Она
является однопараметрическим множеством (этим единственным
параметром является расстояние между двумя точками)
Z
П2
В2 В
А2
А
l2
X
l
O
l1
В1
А1
Прямая может быть задана:
o Двумя точками (см. А и В)
o Точкой и направлением (вектором, лучом)
o Точкой и углами наклона к плоскостям
проекций
o Как результат взаимного пересечения двух
плоскостей
Часто прямую линию
задают начертанием
и обозначают одним
символом, например, l
5
Y
4.
Комплексный чертеж прямой линииZ
l2
l3
А3
А2
В2
В3
П2
X
П1
O
П3
У
В1
l1
А1
У
4
5.
Принадлежность точки прямой линииОсновополагающее положение (запомните
его!): ТОЧКА ПРИНАДЛЕЖИТ ПРЯМОЙ,
ЕСЛИ ЕЁ ПРОЕКЦИИ ПРИНАДЛЕЖАТ
ОДНОИМЕННЫМ ПРОЕКЦИЯМ ЭТОЙ
ПРЯМОЙ
(см. А1 принадлежит l1 , A2 принадлежит l2)
l2
А2
П2
X
П1
l1
о
линия проекционной связи
Не забывайте, что проекции
точки А1 и А2 имеют линию
проекционной связи, которая
перпендикулярна оси проекций,
т.е. (А1-А2)⊥ох
А1
5
6.
Положение прямой относительноплоскостей проекций
Прямая общего положения
Z
П2
В2 В
А2
А
l2
X
l
O
l1
В1
А1
Прямая линия не параллельная (естественно,
и не перпендикулярная) ни к одной из
плоскостей проекций называется – прямой
общего положения (произвольного
расположения)
Проекционное свойство прямой
линии общего положения:
На комплексном чертеже
проекции прямой линии общего
положения не параллельны и не
перпендикулярны ни к одной из
осей проекций
Y
5
7.
Комплексный чертеж прямой общегоположения
Z
l2
l3
А3
А2
В2
В3
П2
X
П1
O
П3
У
Ещё раз запоминаем!
Проекционное свойство прямой линии
общего положения:
На комплексном чертеже проекции
прямой общего положения не
параллельны и не перпендикулярны ни к
одной из осей проекций
В1
l1
А1
У
4
8.
Положение прямой относительноплоскостей проекций
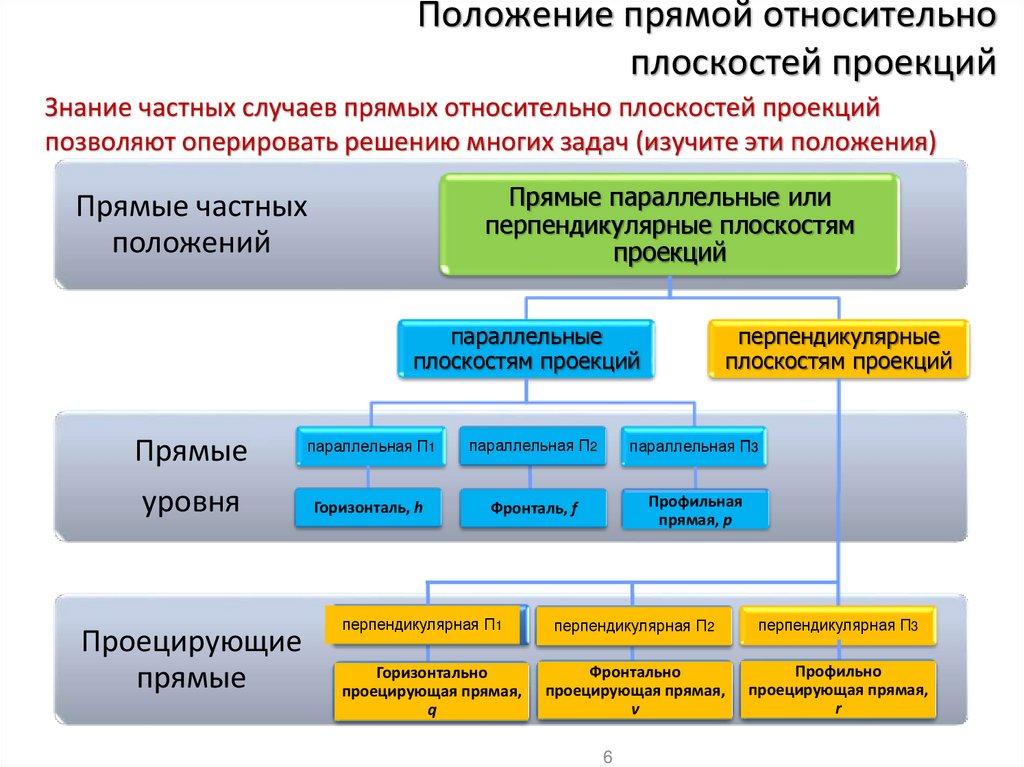
Знание частных случаев прямых относительно плоскостей проекций
позволяют оперировать решению многих задач (изучите эти положения)
Прямые параллельные или
перпендикулярные плоскостям
проекций
Прямые частных
положений
параллельные
плоскостям проекций
перпендикулярные
плоскостям проекций
Прямые
параллельная П1
параллельная П2
параллельная П3
уровня
Горизонталь, h
Фронталь, f
Профильная
прямая, p
Проецирующие
прямые
перпендикулярная П1
перпендикулярная П2
перпендикулярная П3
Горизонтально
проецирующая прямая,
q
Фронтально
проецирующая прямая,
v
Профильно
проецирующая прямая,
r
6
9.
Положение прямой относительноплоскостей проекций
Прямые уровня
Прямой
уровня
называется
прямая,
параллельная к одной из плоскостей
проекций.
На самом деле, пусть прямая параллельна
П1, тогда, каждая, именно каждая точка на
этой прямой, имеет одинаковую высоту
относительно П1 (одинаковую координату Z
каждой точки), т.е. имеет один уровень
относительно плоскости П1.
7
10.
Положение прямой относительноплоскостей проекций
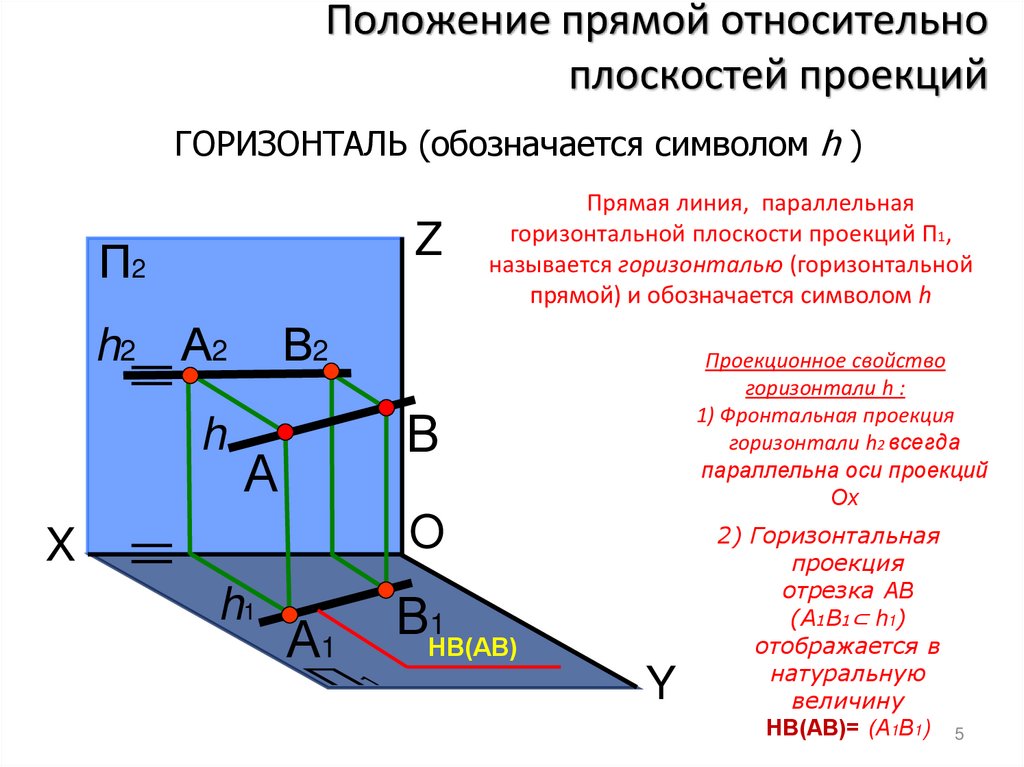
ГОРИЗОНТАЛЬ (обозначается символом h )
П2
h2
А2
h
Z
Прямая линия, параллельная
горизонтальной плоскости проекций П1,
называется горизонталью (горизонтальной
прямой) и обозначается символом h
В
Проекционное свойство
горизонтали h :
1) Фронтальная проекция
горизонтали h2 всегда
параллельна оси проекций
Ох
В2
А
O
X
h1
А1
ВНВ(АВ)
1
Y
2) Горизонтальная
проекция
отрезка АВ
(А1В1⊂ h1)
отображается в
натуральную
величину
НВ(АВ)= (А1В1) 5
11.
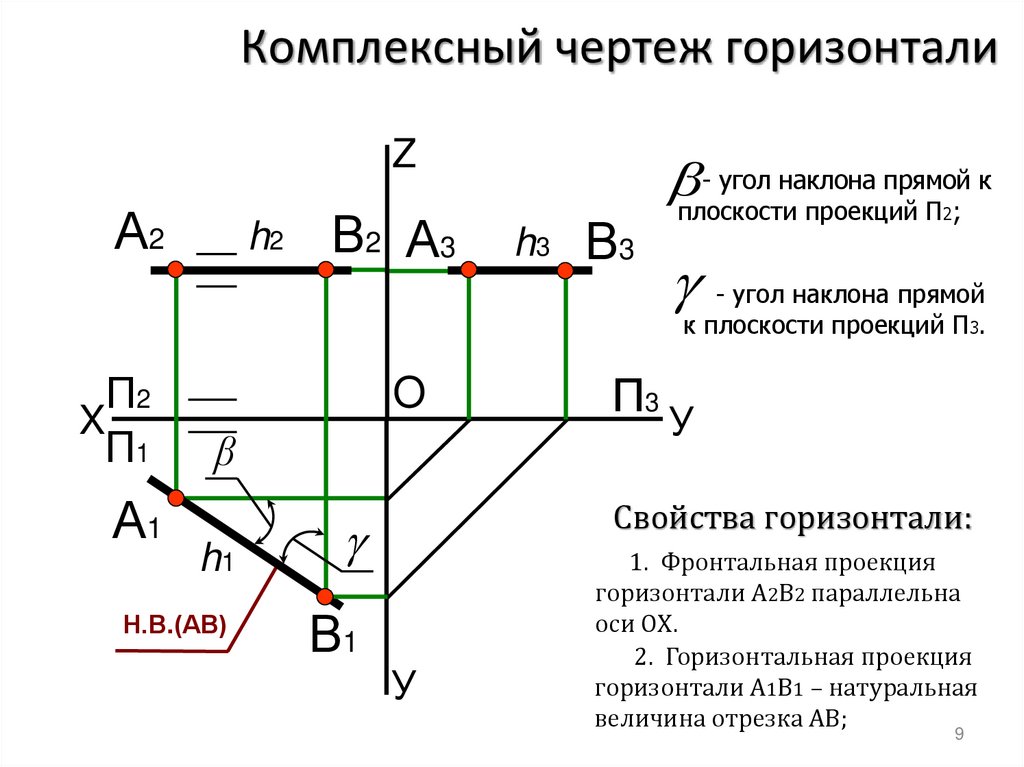
Комплексный чертеж горизонталиZ
А2
h2
В2 А3
β- угол наклона прямой к
h3
В3
плоскости проекций П2;
- угол наклона прямой
к плоскости проекций П3.
П2
X
П1
А1
O
β
h1
Н.В.(АВ)
П3
У
Свойства горизонтали:
В1
У
1. Фронтальная проекция
горизонтали А2В2 параллельна
оси ОХ.
2. Горизонтальная проекция
горизонтали А1В1 – натуральная
величина отрезка АВ;
9
12.
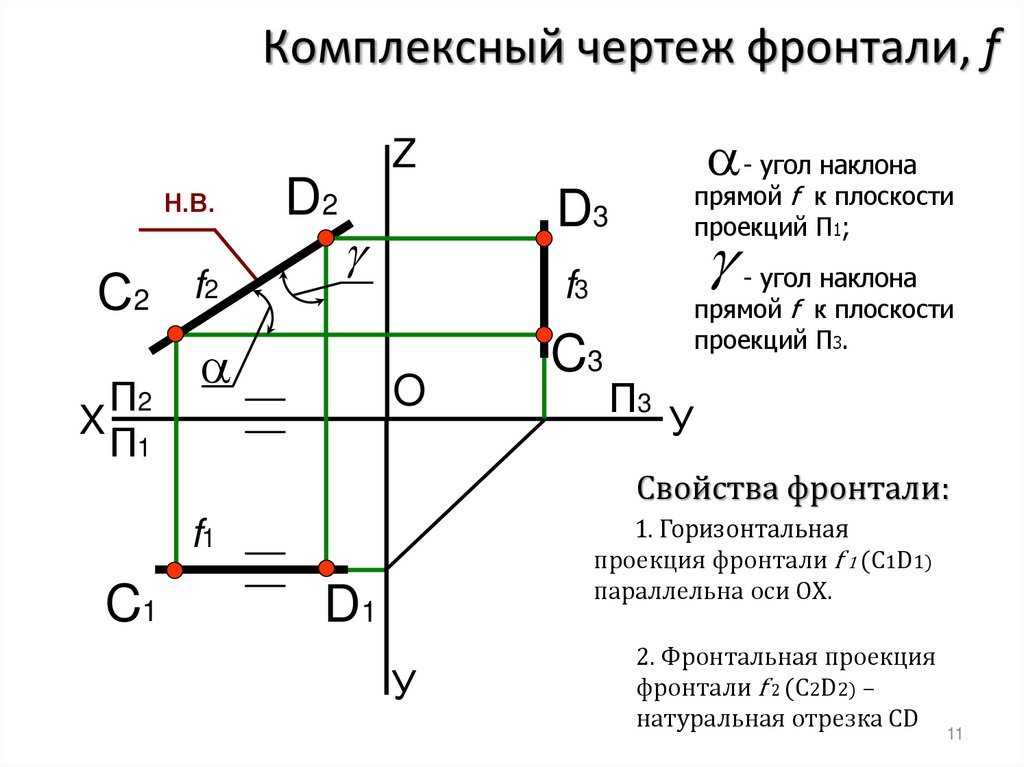
Комплексный чертеж фронтали, f- угол наклона
Z
Н.В.
С2
П2
X
П1
f2
D2
прямой f к плоскости
проекций П1;
D3
- угол наклона
f3
O
C3
прямой f к плоскости
проекций П3.
П3
У
Свойства фронтали:
1. Горизонтальная
проекция фронтали f 1 (C1D1)
параллельна оси ОХ.
f1
C1
D1
У
2. Фронтальная проекция
фронтали f 2 (C2D2) –
натуральная отрезка СD
11
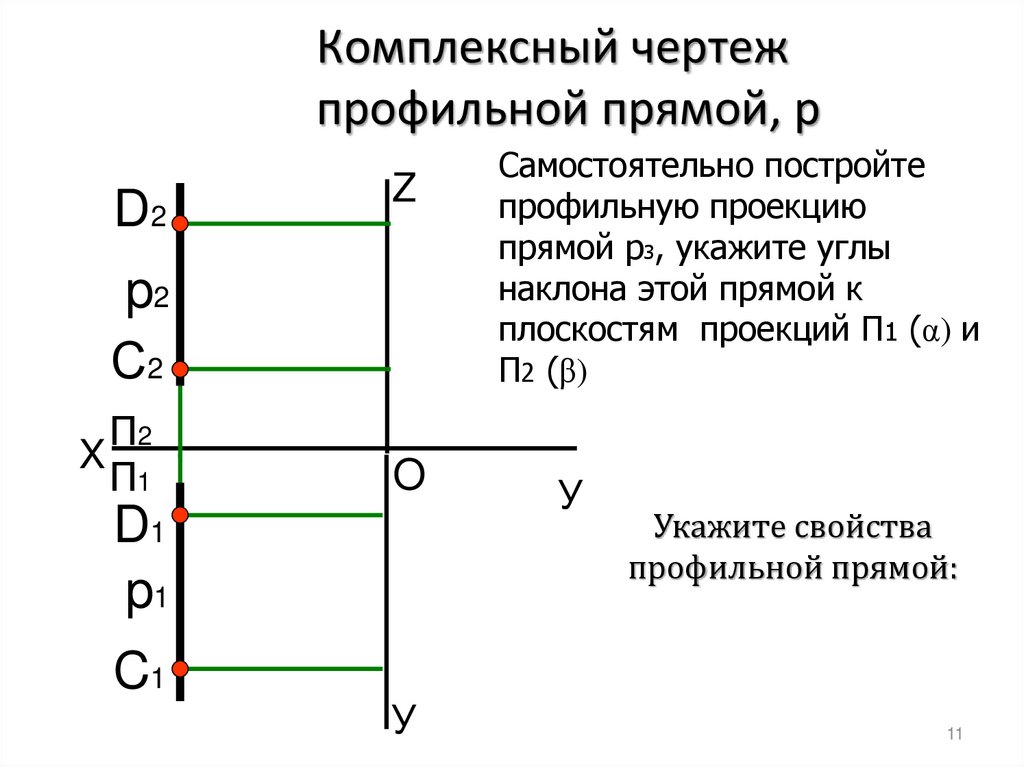
13.
Комплексный чертежпрофильной прямой, p
D2
Z
p2
С2
П2
X
П1
O
D1
p1
C1
У
Самостоятельно постройте
профильную проекцию
прямой p3, укажите углы
наклона этой прямой к
плоскостям проекций П1 (α) и
П2 (β)
У
Укажите свойства
профильной прямой:
11
14.
Проецирующие прямыеПроецирующие прямые – это прямые совпадающие
с направлением проецирования
Так как в методе Монжа проецирующий луч перпендикулярен к плоскостям
проекций, то проецирующие прямые также перпендикулярны
к плоскостям проекций
П2
q2 А2
Н.В.
В2
X
q – горизонтально проецирующая прямая
Эта прямая перпендикулярна
горизонтальной плоскости проекций П1 и
проецируется на неё в точку (q₁)
А
Фронтальная проекция (q₂)
перпендикулярна оси проекций ОХ, на этой
же проекции отрезок АВ прямой
q
проецируется в натуральную величину.
Точки А и В являются
В
O
конкурирующими: из-за точки А на
П1 точку В не видно (она находится
под точкой А; это можно судить и по
А1=B1 =q1
фронтальным проекциям этих точек
Z
Y
5
15.
А2Комплексный чертеж горизонтально
проецирующей прямой
Z
q2
А3 q3
Н.В.(АВ)
Какие свойства
данной прямой q
можно отметить?
Н.В.(АВ)
В2
O
В3
У
X
Чему равны углы
наклона прямой q к
плоскостям
проекций?
А1=B1=q1
У
9
16.
Комплексный чертеж фронтальнопроецирующей прямой
Z
А2=B2=v2
Самостоятельно достройте
профильную проекцию
прямой v
O
У
X
В1
Н.В.(АВ)
А1
Какие свойства
данной прямой v
можно отметить?
Чему равны углы
наклона прямой v
к плоскостям
проекций?
v1
У
9
17.
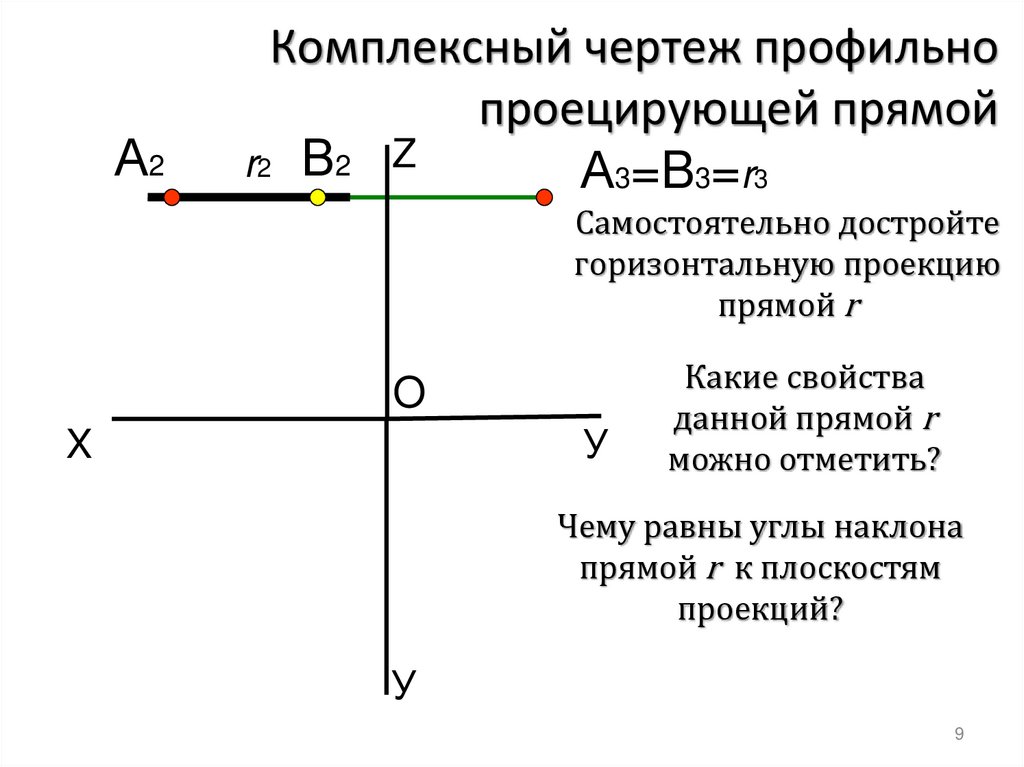
А2Комплексный чертеж профильно
проецирующей прямой
r2 В2 Z
А3=B3=r3
Самостоятельно достройте
горизонтальную проекцию
прямой r
O
У
X
Какие свойства
данной прямой r
можно отметить?
Чему равны углы наклона
прямой r к плоскостям
проекций?
У
9
18.
Взаимное положение точки ипрямой
41
А2
12
22
В2
32
11 (A1B1) т.1 (AB)
12 (A2B2)
X
А1
21 (A1B1) т.2 (AB)
22 (A2B2)
21
11
31
Если точка принадлежит
прямой, то проекции этой
точки принадлежат
одноименным проекциям
прямой
42 В1
31 (A1B1) т.3 (AB)
32 (A2B2)
41 (A1B1) т.4 (AB)
42 (A2B2)
17
19.
Взаимное положение точки ипрямой
D2
B2
l2 А2
E2
В – над прямой l, B l
C2
С – под прямой l, С l
X
l1 А1
A – принадлежит
прямой l, A l
D – перед прямой l, D l
B1
E1
C1
Е – за прямой l, E l
D1
17
20.
Взаимное положение точки ипрямой
S1
l2
А2 P1
T1
R1
V1
V2
X
l1 А1
А-?
P-?
R-?
S-?
T-?
W1
V-?
S2
P2
T2
W2
W-?
R2
17
21.
Взаимное расположение двух прямыхПрямые в пространстве
могут быть:
• Пересекающимися
• Параллельными
• Скрещивающимися
22.
Пересекающиеся прямыеПересекающиеся прямые –
это прямые имеющие одну
общую собственную точку,
т.е. точку их взаимного
пересечения.
На чертеже проекции этой
точки находятся на одной
линии проекционной связи.
23.
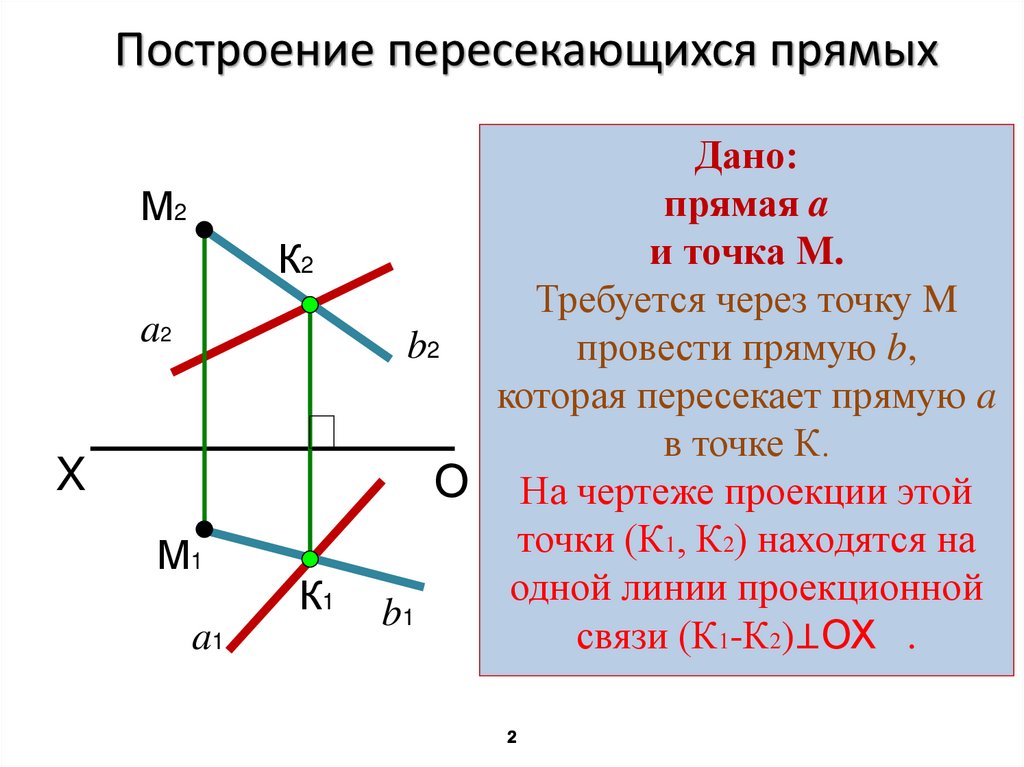
Построение пересекающихся прямыхМ2
К2
a2
X
М1
a1
К1
Дано:
прямая a
и точка M.
Требуется через точку M
b2
провести прямую b,
которая пересекает прямую a
в точке К.
О На чертеже проекции этой
точки (К1, К2) находятся на
одной линии проекционной
b1
связи (К1-К2)⊥ОХ .
24.
Параллельные прямыеПараллельные прямые – это
прямые имеющие одну
общую несобственную точку
(бесконечно удаленную
точку)
На чертеже одноименные
проекции таких прямых
взаимно параллельны
25.
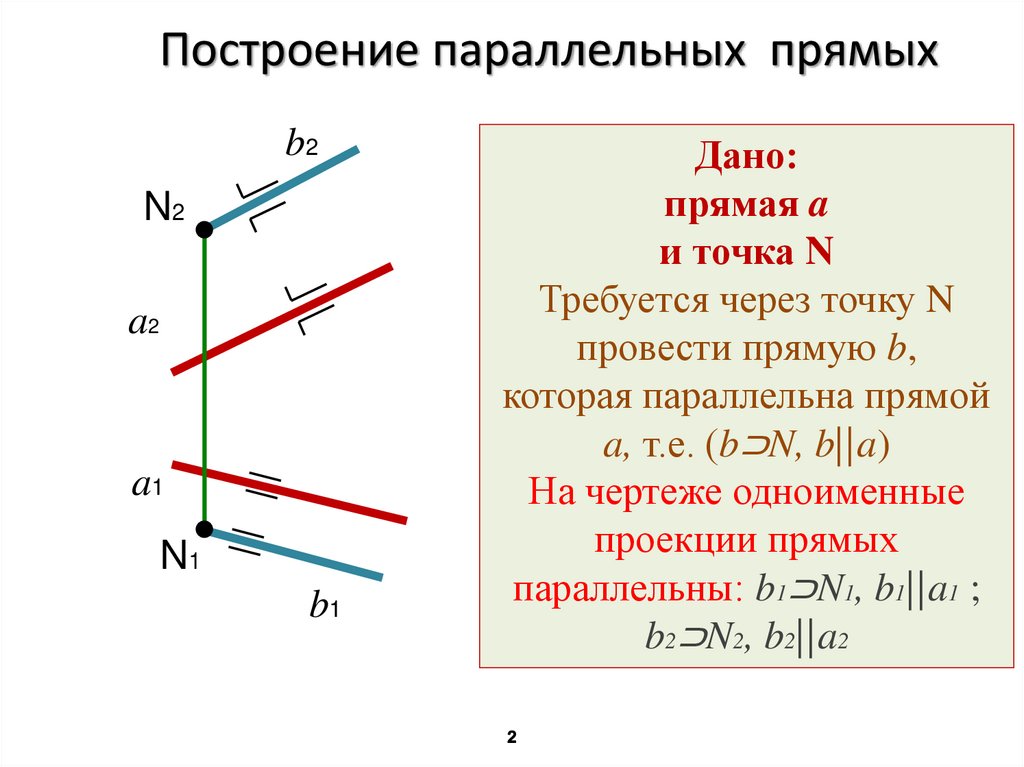
Построение параллельных прямыхb2
N2
a2
a1
N1
b1
Дано:
прямая a
и точка N
Требуется через точку N
провести прямую b,
которая параллельна прямой
a, т.е. (b⊃N, b||a)
На чертеже одноименные
проекции прямых
параллельны: b1⊃N1, b1||a1 ;
b2⊃N2, b2||a2
26.
Скрещивающиеся прямыеСкрещивающиеся прямые – это
прямые не имеющие общей
точки
На скрещивающихся прямых
линиях рассматривают
конкурирующие точки, при
помощи которых
устанавливается видимость на
чертеже
27.
Построение скрещивающихся прямыхb2
a2
32=42
12
22
X
31
a1
11=21 41
b1
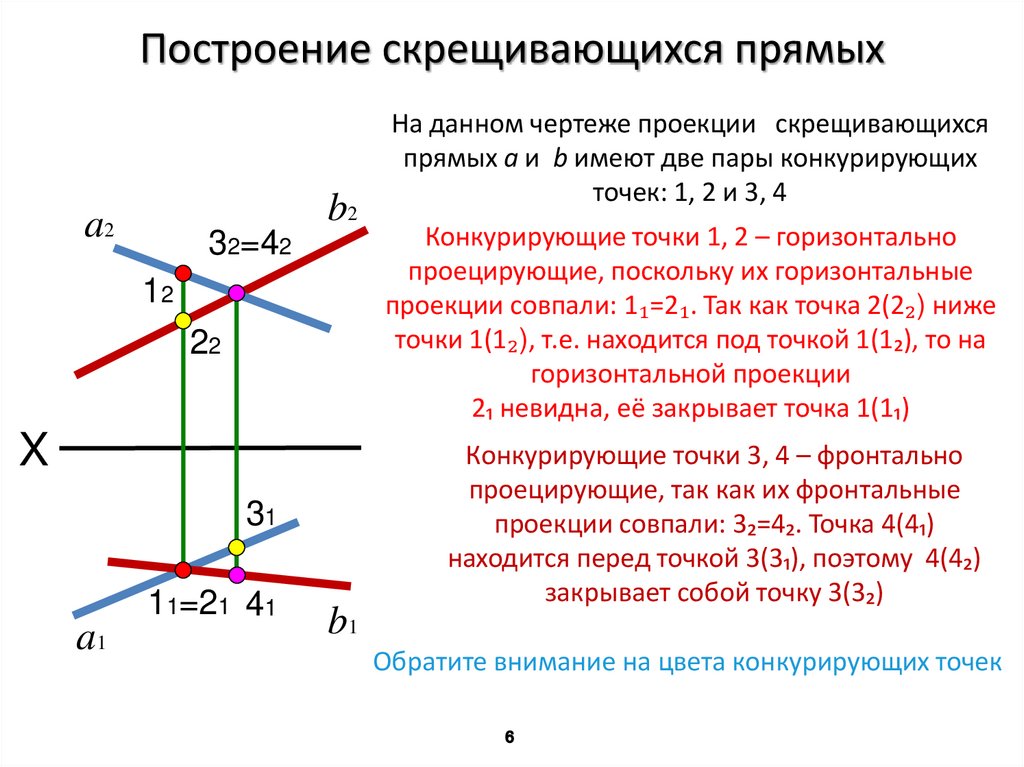
На данном чертеже проекции скрещивающихся
прямых a и b имеют две пары конкурирующих
точек: 1, 2 и 3, 4
Конкурирующие точки 1, 2 – горизонтально
проецирующие, поскольку их горизонтальные
проекции совпали: 1₁=2₁. Так как точка 2(2₂) ниже
точки 1(1₂), т.е. находится под точкой 1(1₂), то на
горизонтальной проекции
2₁ невидна, её закрывает точка 1(1₁)
Конкурирующие точки 3, 4 – фронтально
проецирующие, так как их фронтальные
проекции совпали: 3₂=4₂. Точка 4(4₁)
находится перед точкой 3(3₁), поэтому 4(4₂)
закрывает собой точку 3(3₂)
Обратите внимание на цвета конкурирующих точек
















 mathematics
mathematics drafting
drafting








