Виды проецирования. Точка, прямая

1.

Кафедра графики
Татьяна Васильевна Андрюшина
Практическое занятие 1
по начертательной геометрии
для студентов 1 курса
Виды проецирования.
Точка, прямая
Новосибирск, 2024

2.

«Очарование, сопровождающее науку,
может
победить
свойственное
людям отвращение к напряжению
ума и заставить их находить
удовольствие в упражнении своего
разума…»
Гаспар Монж
Основоположником начертательной геометрии и
метода ортогонального проецирования является
французский математик, геометр Гаспар Монж
(1746-1818 гг.).

3.

План занятия
• Предмет начертательная геометрия
• Виды проецирования. Свойства ортогонального проецирования
• Образование комплексного чертежа. Комплексный чертеж то
• Комплексный чертеж линии. Взаимное расположение
прямых
• Положение прямых линий относительно плоскостей
проекций
3

4.

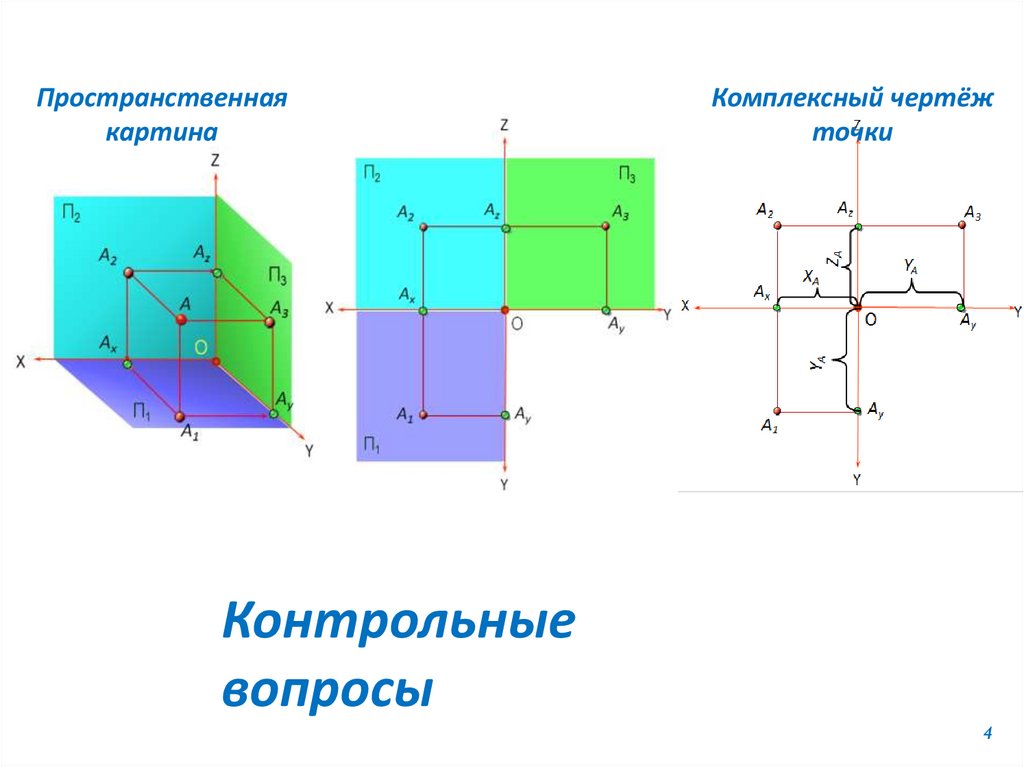
Пространственная
картина
Комплексный чертёж
точки
Контрольные
вопросы
4

5.

Что называется
проецированием?
Проецирование
это
процесс
получения
изображения предмета на какой-либо поверхности,
в том числе на плоскости.
Что называется проекцией
предмета?
Проекцией предмета называют получившееся
при проецировании изображение.
Слово "проекция" в переводе с
означает "бросание вперёд, вдаль".
латинского
5

6.

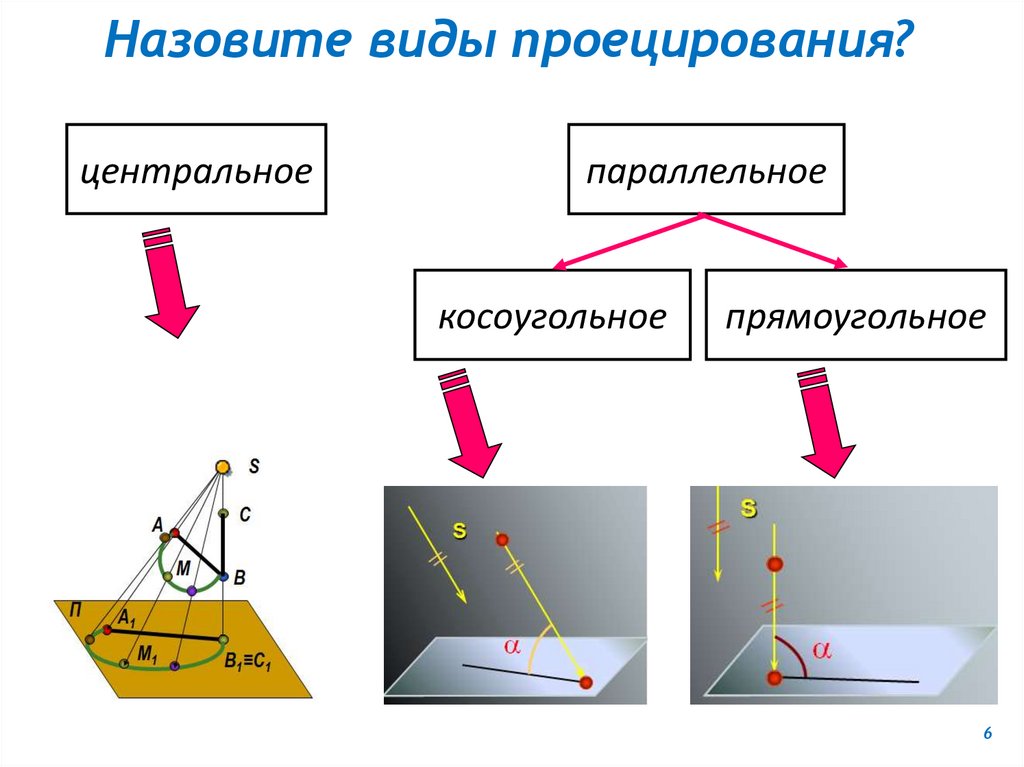
Назовите виды проецирования?
центральное
параллельное
косоугольное
прямоугольное
6

7.

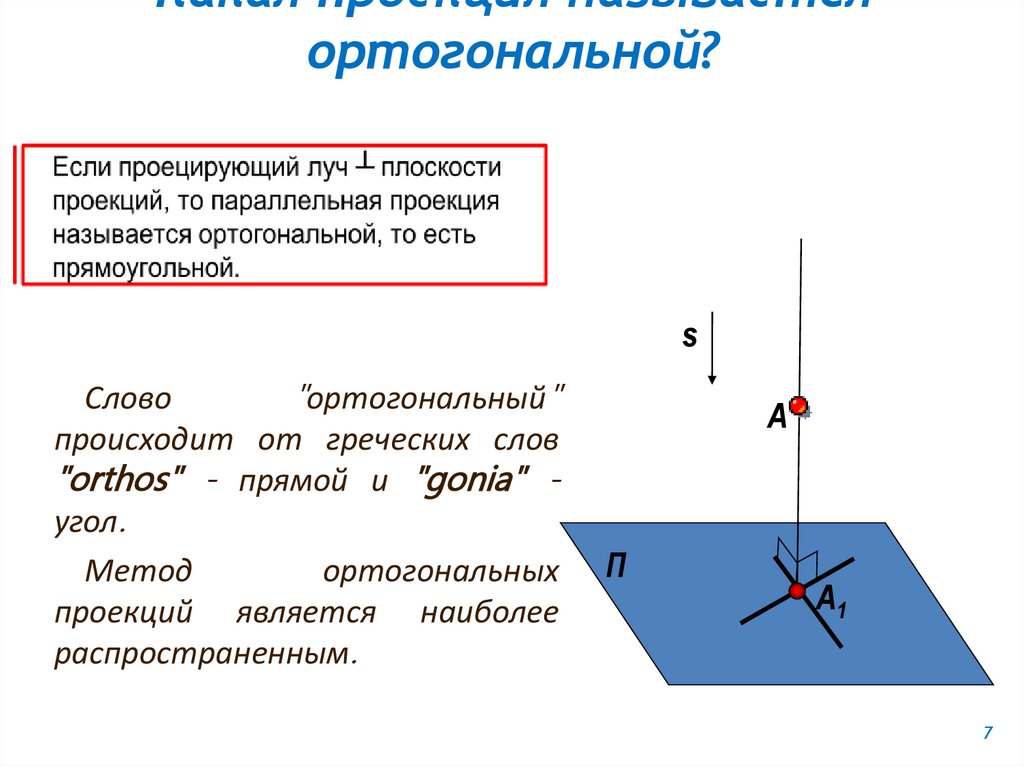
Какая проекция называется
ортогональной?
s
Слово
"ортогональный"
происходит от греческих слов
"orthos" - прямой и "gonia" угол.
Метод
ортогональных
проекций является наиболее
распространенным.
А
П
А1
7

8.

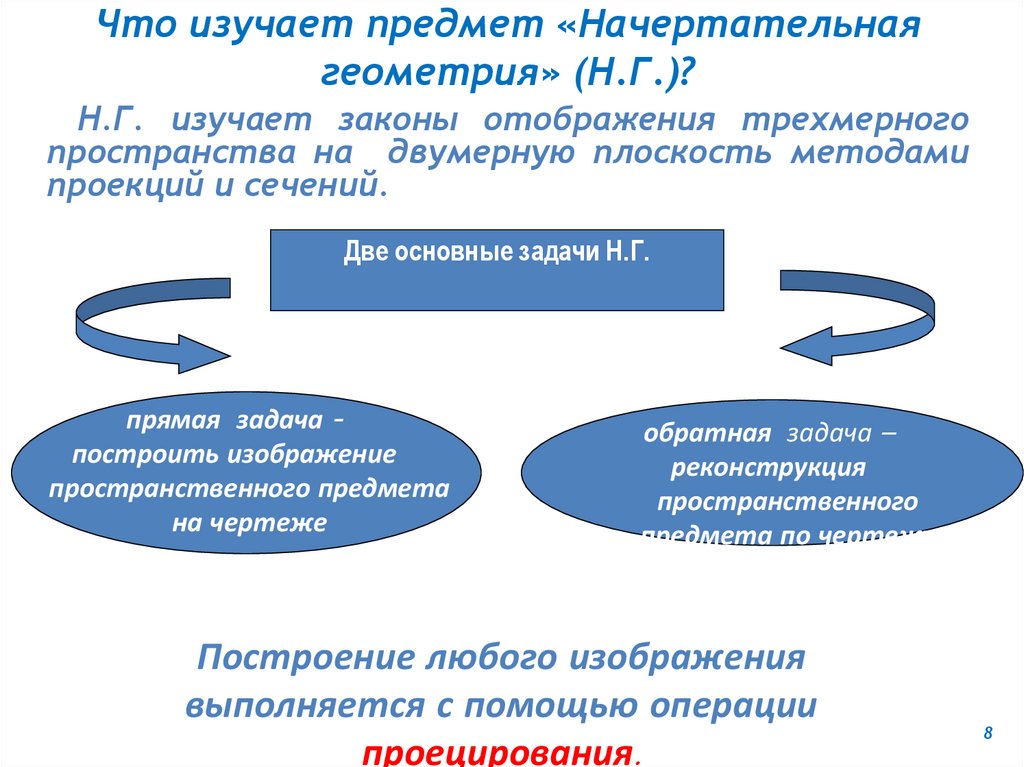
Что изучает предмет «Начертательная
геометрия» (Н.Г.)?
Н.Г. изучает законы отображения трехмерного
пространства на двумерную плоскость методами
проекций и сечений.
Две основные задачи Н.Г.
прямая задача построить изображение
пространственного предмета
на чертеже
обратная задача –
реконструкция
пространственного
предмета по чертежу
Построение любого изображения
выполняется с помощью операции
проецирования.
8

9.

Назовите основные задачи начертательной геометри
1. Создание плоской геометрической модели
пространственного объекта – чертежа
(эпюра).
Эпюр – в переводе с греческого – чертеж или
проект.
2. Решение задач на плоскости.
3. Чтение чертежа (эпюра).

10.

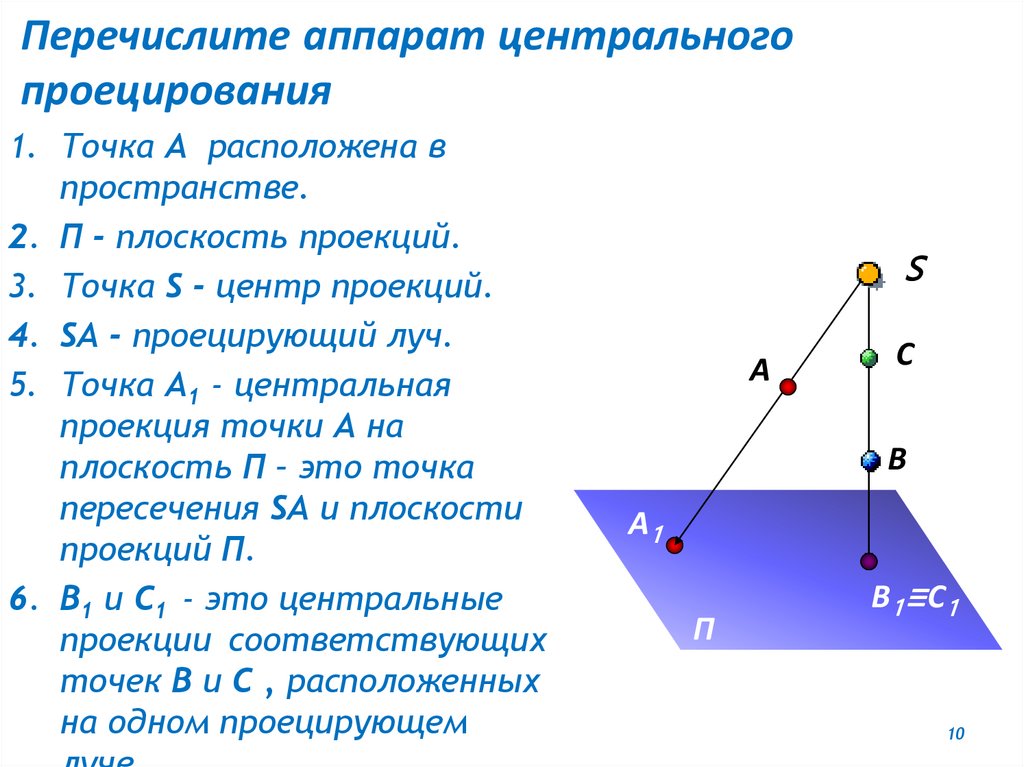
Перечислите аппарат центрального
проецирования
1. Точка А расположена в
пространстве.
2. П - плоскость проекций.
3. Точка S - центр проекций.
4. SА - проецирующий луч.
5. Точка А1 - центральная
проекция точки А на
плоскость П – это точка
пересечения SА и плоскости
проекций П.
6. B1 и C1 - это центральные
проекции соответствующих
точек B и C , расположенных
на одном проецирующем
S
А
С
В
А1
П
В1≡С1
10

11.

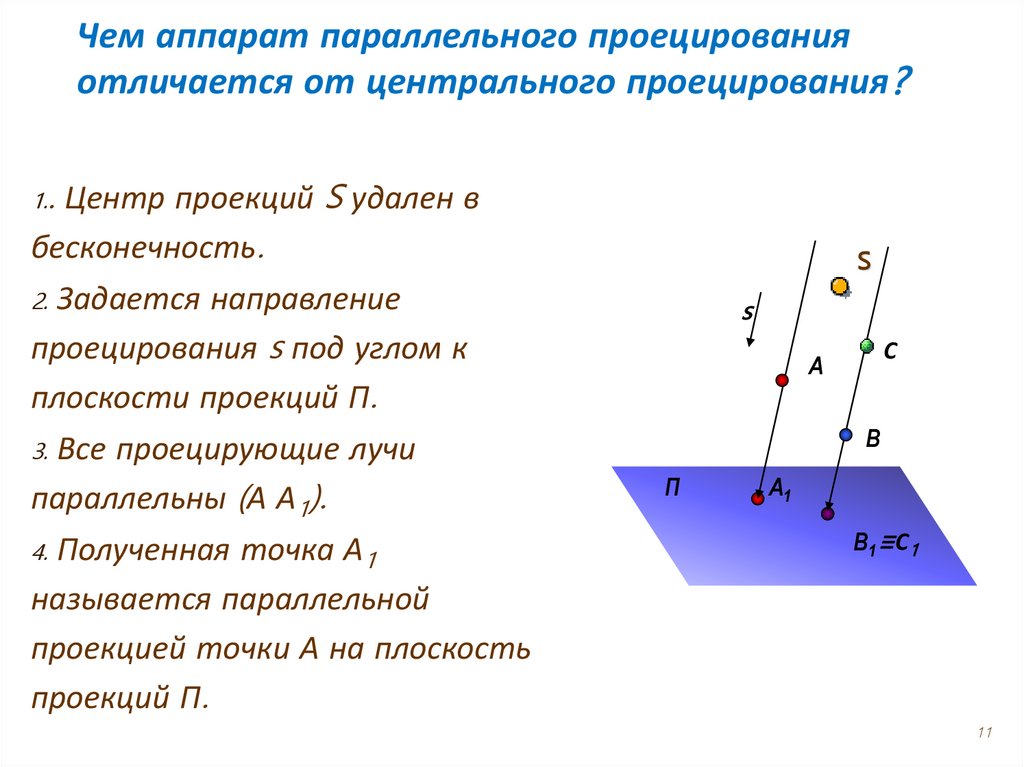
Чем аппарат параллельного проецирования
отличается от центрального проецирования?
1.. Центр проекций S удален в
бесконечность.
2. Задается направление
проецирования s под углом к
плоскости проекций П.
3. Все проецирующие лучи
параллельны (А А1).
4. Полученная точка А1
называется параллельной
проекцией точки А на плоскость
проекций П.
S
s
С
А
В
П
А1
В 1 ≡ С1
11

12.

12

13.

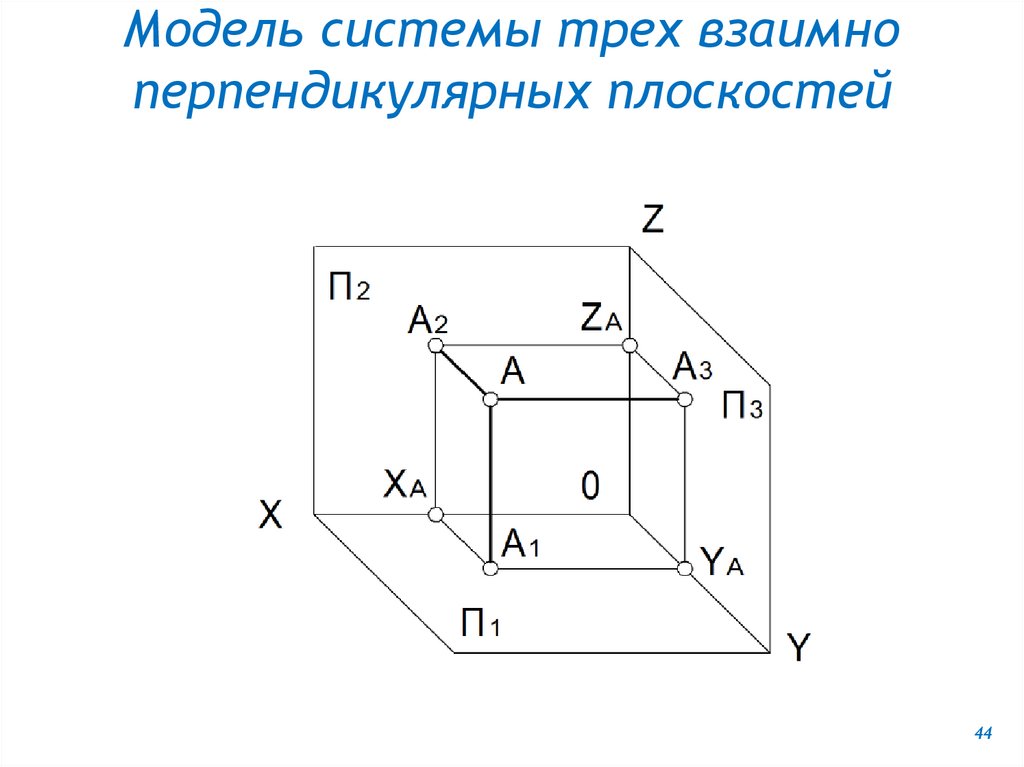
Как располагаются основные
плоскости проекций?
Три плоскости П1 , П2 , П3 взаимно
перпендикулярны:
П1 П2
П3
П2
П3
П1
перпендикулярна одновременно
плоскостям П1 и П2 .
13

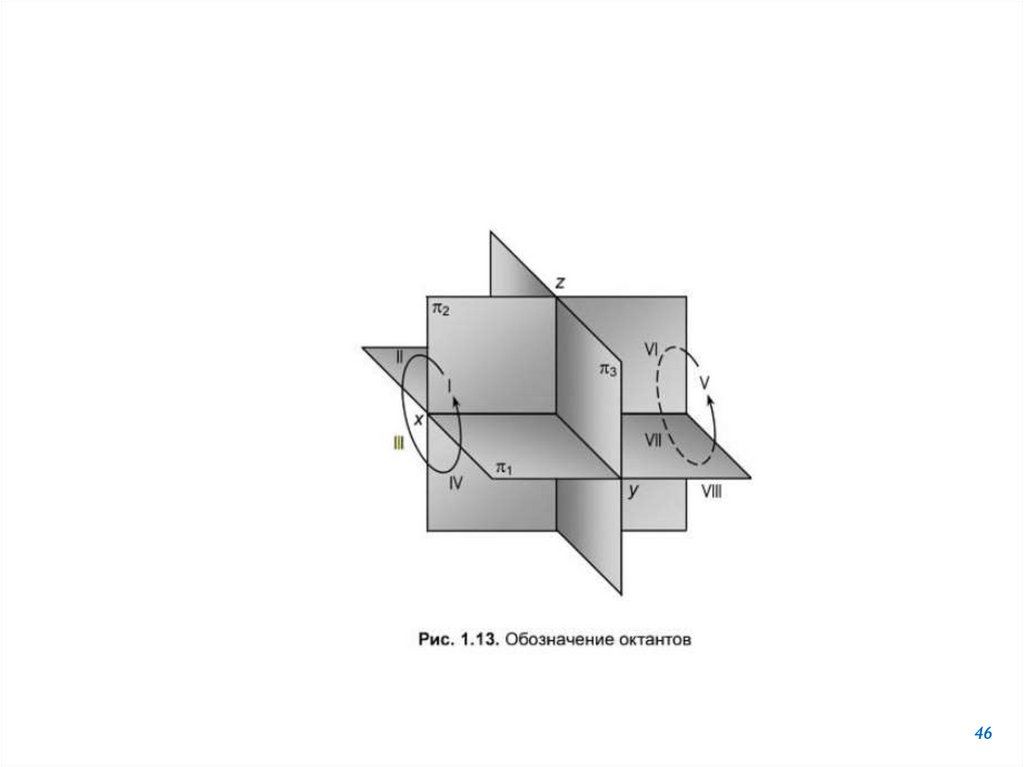
14.

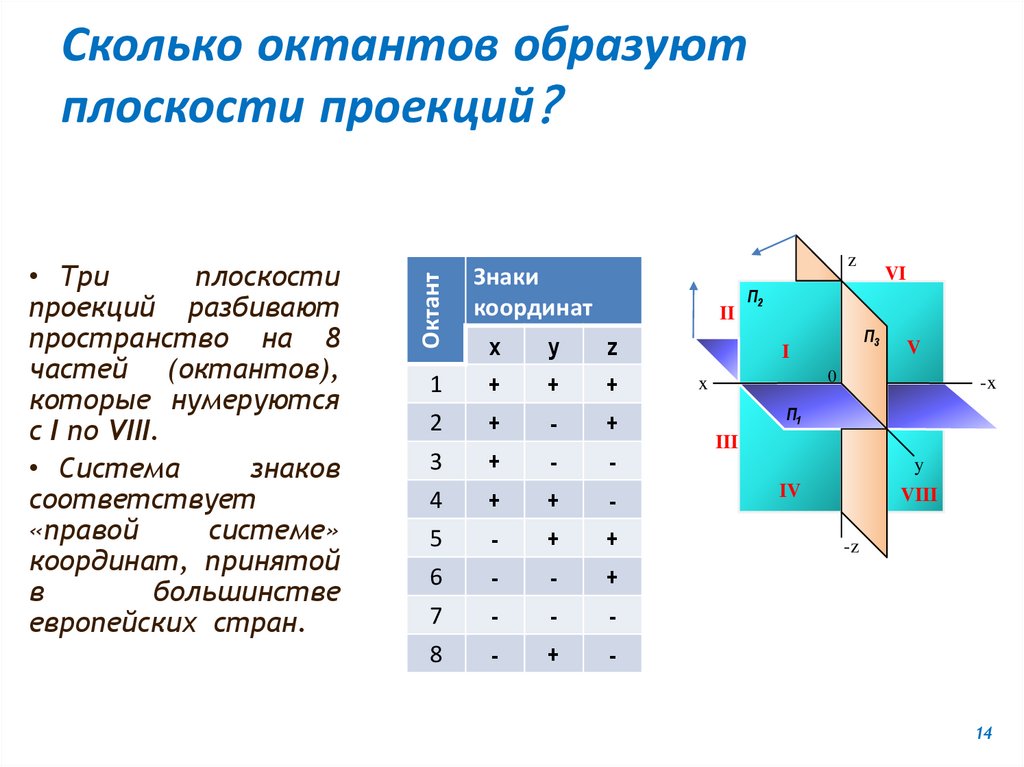
• Три
плоскости
проекций разбивают
пространство на 8
частей (октантов),
которые нумеруются
с I по VIII.
• Система
знаков
соответствует
«правой
системе»
координат, принятой
в
большинстве
европейских стран.
Октант
Сколько октантов образуют
плоскости проекций?
z
Знаки
координат
II
1
x
+
y
+
z
+
2
3
4
5
+
+
+
-
+
+
+
+
6
7
8
-
+
+
-
VI
П2
П3
I
V
0
x
-x
П1
III
y
IV
VIII
-z
14

15.

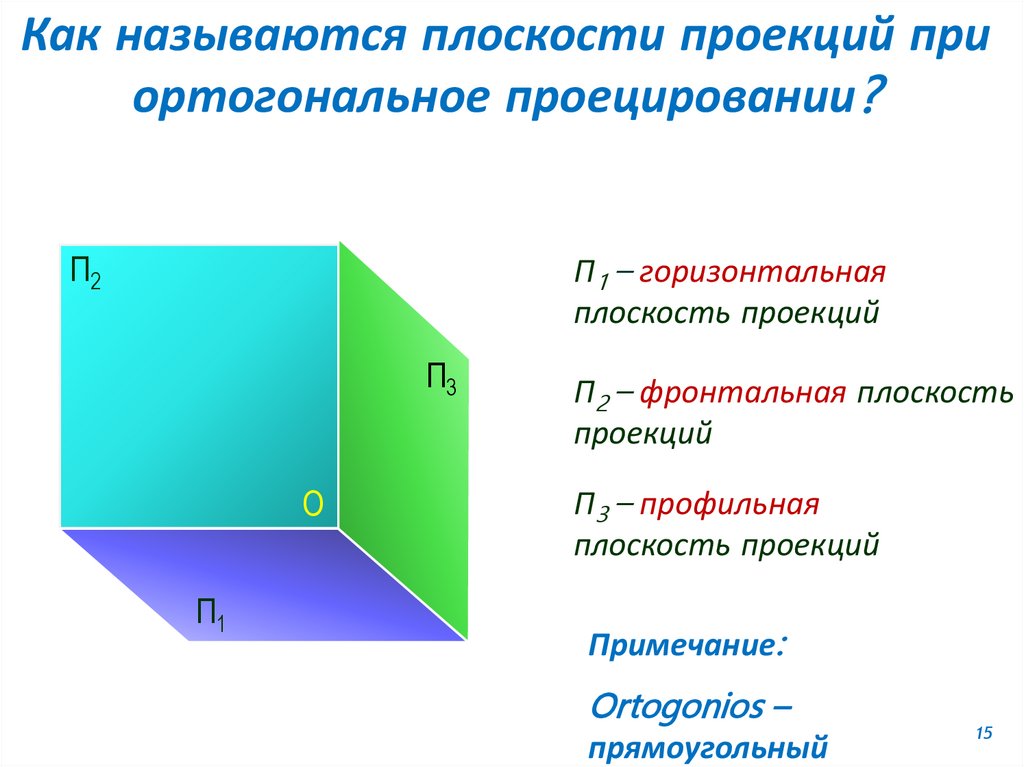
Как называются плоскости проекций при
ортогональное проецировании?
П1 – горизонтальная
плоскость проекций
П2
П3
О
П1
П2 – фронтальная плоскость
проекций
П3 – профильная
плоскость проекций
Примечание:
Ortogonios –
прямоугольный
15

16.

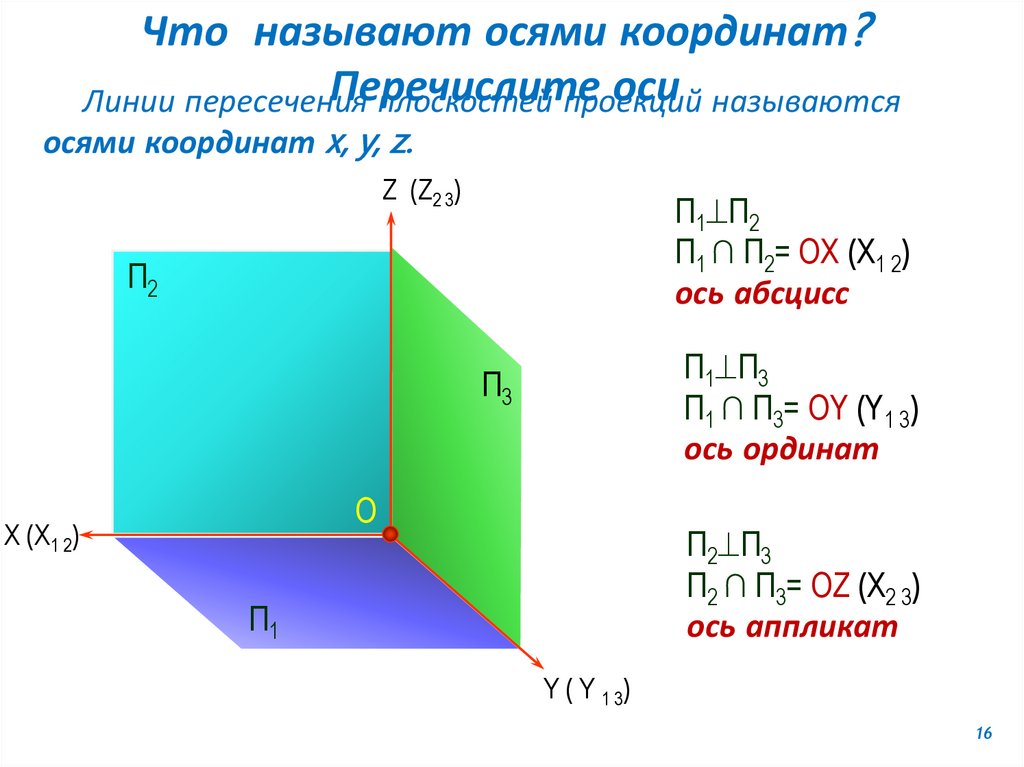
Что называют осями координат?
Перечислите
оси называются
Линии пересечения
плоскостей проекций
осями координат x, y, z.
Z (Z2 3)
П1 П2
П1 ∩ П2= OX (X1 2)
ось абсцисс
П2
П1 П3
П1 ∩ П3= OY (Y1 3)
ось ординат
П3
О
Х (Х1 2)
П2 П3
П2 ∩ П3= OZ (X2 3)
ось аппликат
П1
Y ( Y 1 3)
16

17.

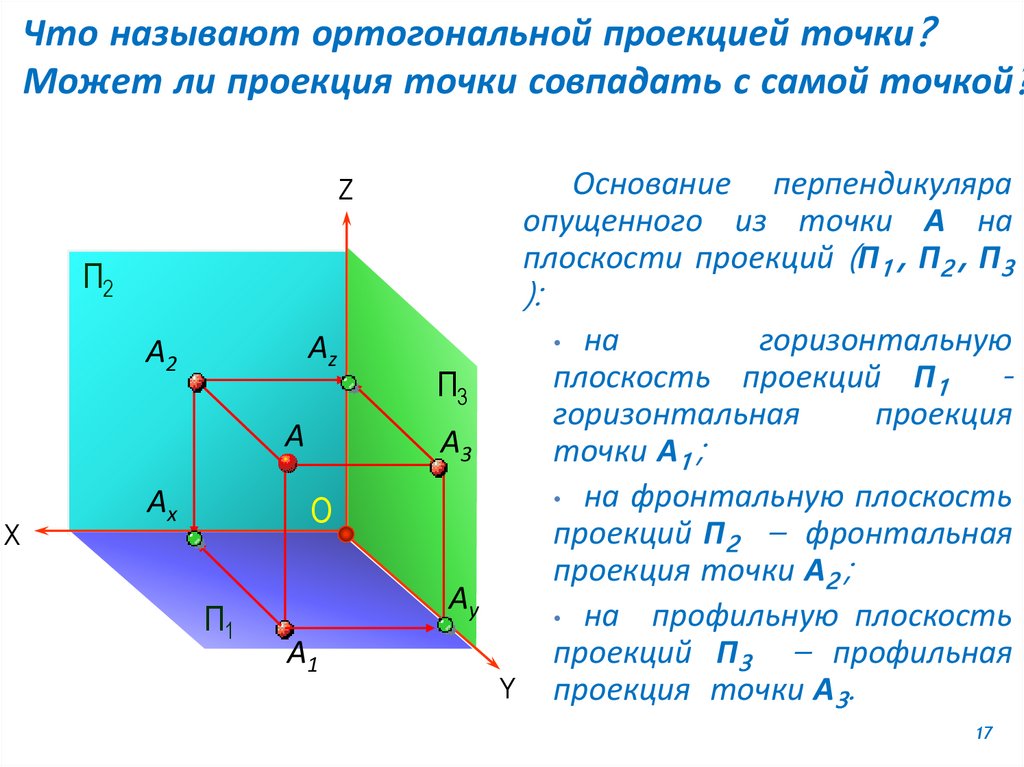
Что называют ортогональной проекцией точки?
Может ли проекция точки совпадать с самой точкой?
Основание перпендикуляра
опущенного из точки А на
плоскости проекций (П1 , П2 , П3
Z
П2
):
Аz
А2
А
Х
Ах
П3
А3
О
П1
Аy
А1
на
горизонтальную
плоскость проекций П1
горизонтальная
проекция
точки А1 ;
• на фронтальную плоскость
проекций П2 – фронтальная
проекция точки А2 ;
• на профильную плоскость
проекций П3 – профильная
проекция точки А3.
Y
17

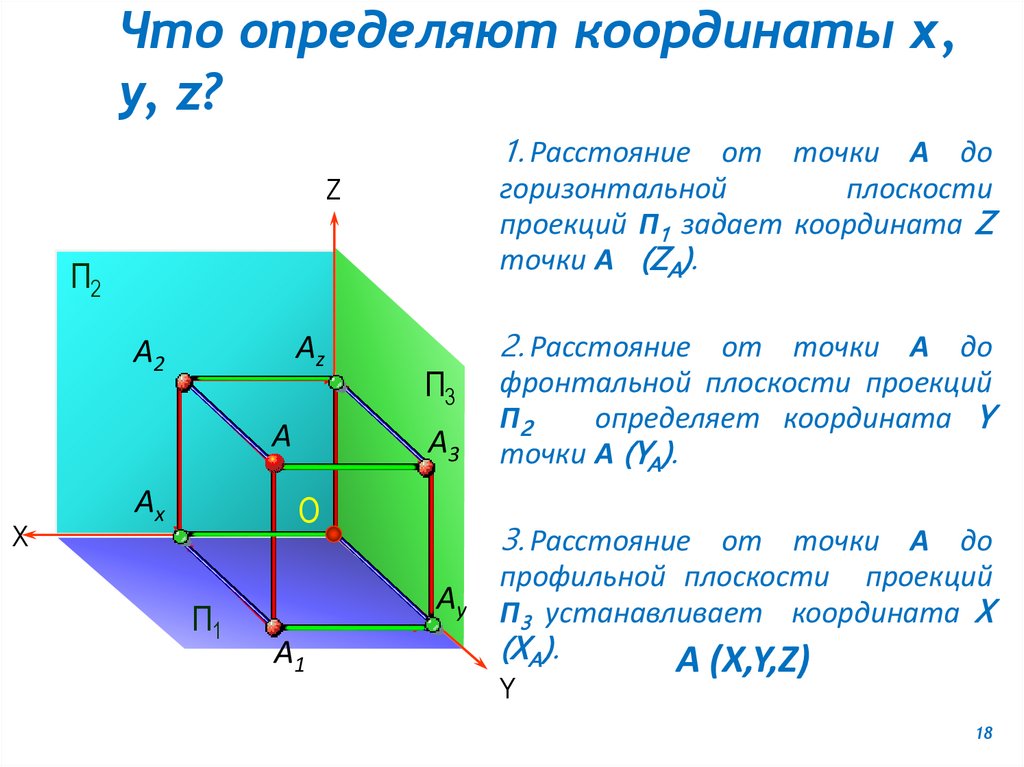
18.

Что определяют координаты x,
y, z?
1. Расстояние от точки А до
Z
горизонтальной
плоскости
проекций П1 задает координата Z
точки А (ZA).
П2
Аz
А2
А
Х
Ах
2. Расстояние от точки А до
П3
А3
О
П1
3. Расстояние от точки А до
Аy
А1
фронтальной плоскости проекций
П2
определяет координата Y
точки А (YA).
профильной плоскости проекций
П3 устанавливает координата X
(XA).
Y
А (X,Y,Z)
18

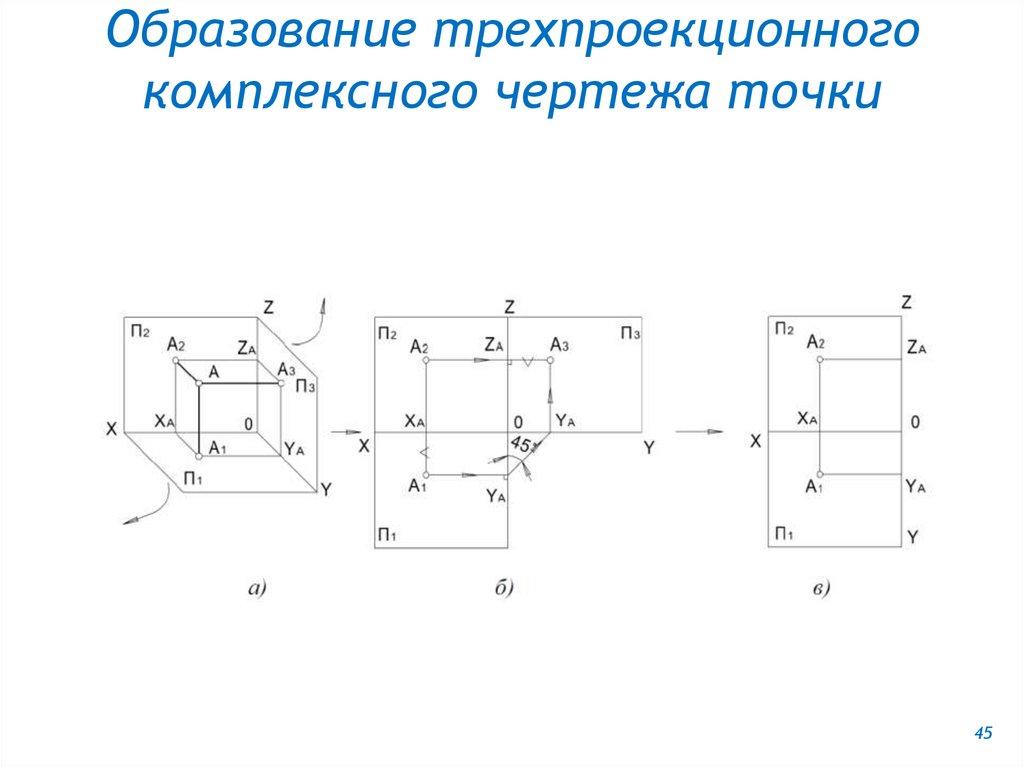
19.

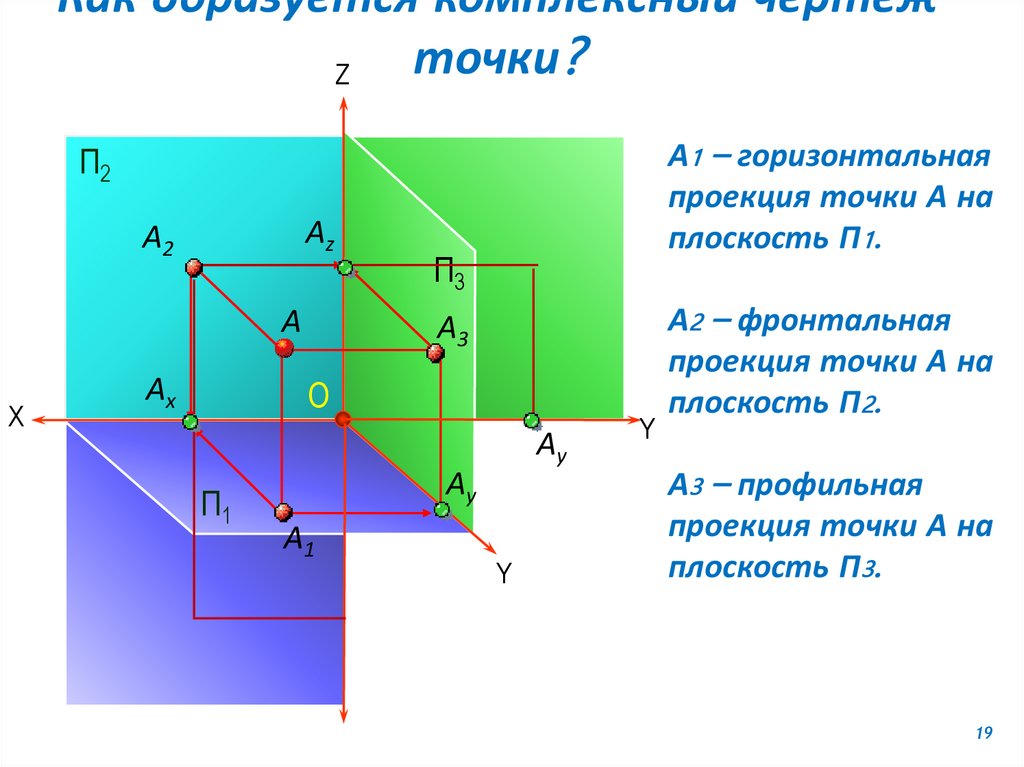
Как образуется комплексный чертеж
точки?
Z
А1 – горизонтальная
проекция точки А на
плоскость П1.
П2
Аz
А2
А
Х
Ах
П3
А3
О
П1
Аy
Аy
А1
Y
Y
А2 – фронтальная
проекция точки А на
плоскость П2.
А3 – профильная
проекция точки А на
плоскость П3.
19

20.

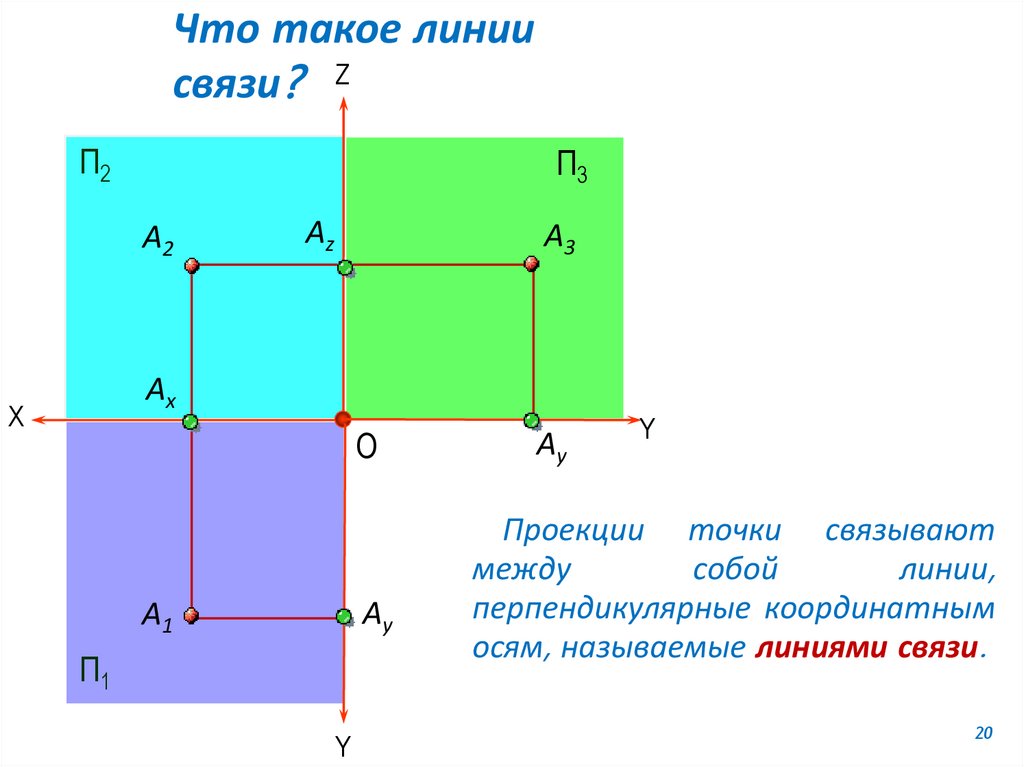
Что такое линии
связи? Z
П2
П3
А2
Аz
А3
Ах
Х
О
Аy
А1
П1
Y
Аy
Y
Проекции точки связывают
между
собой
линии,
перпендикулярные координатным
осям, называемые линиями связи.
20

21.

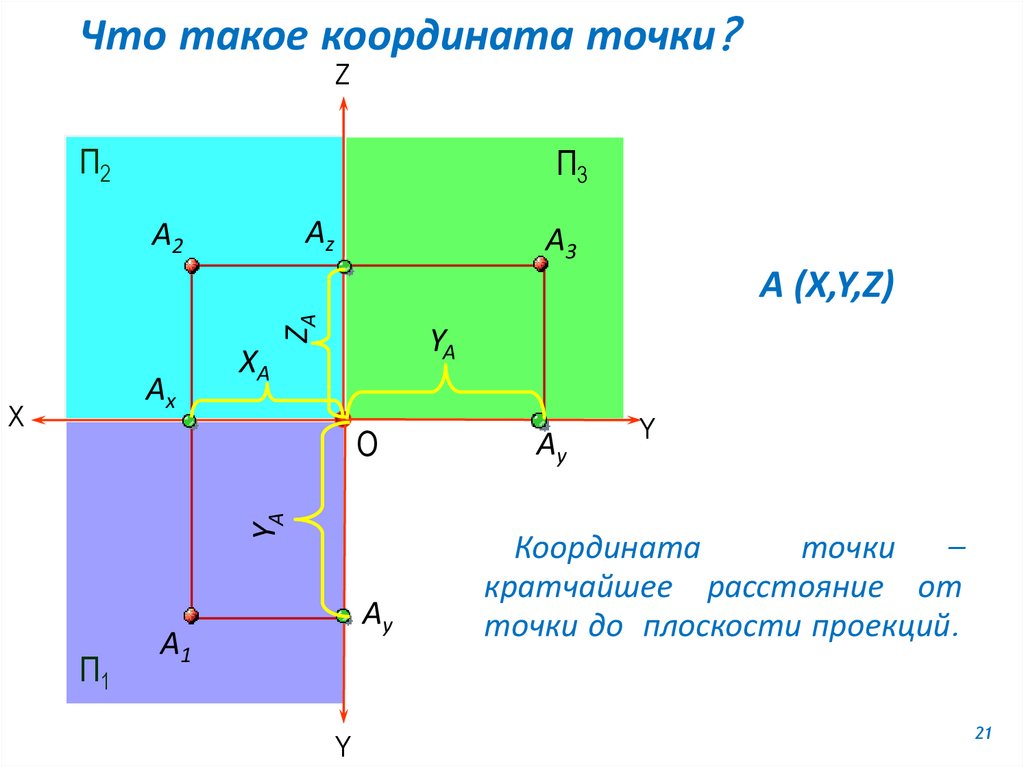
Что такое координата точки?
Z
П2
П3
Аz
А2
А3
ZA
А (X,Y,Z)
Ах
Х
YA
XA
YA
О
П1
Аy
А1
Y
Аy
Y
Координата
точки –
кратчайшее расстояние от
точки до плоскости проекций.
21

22.

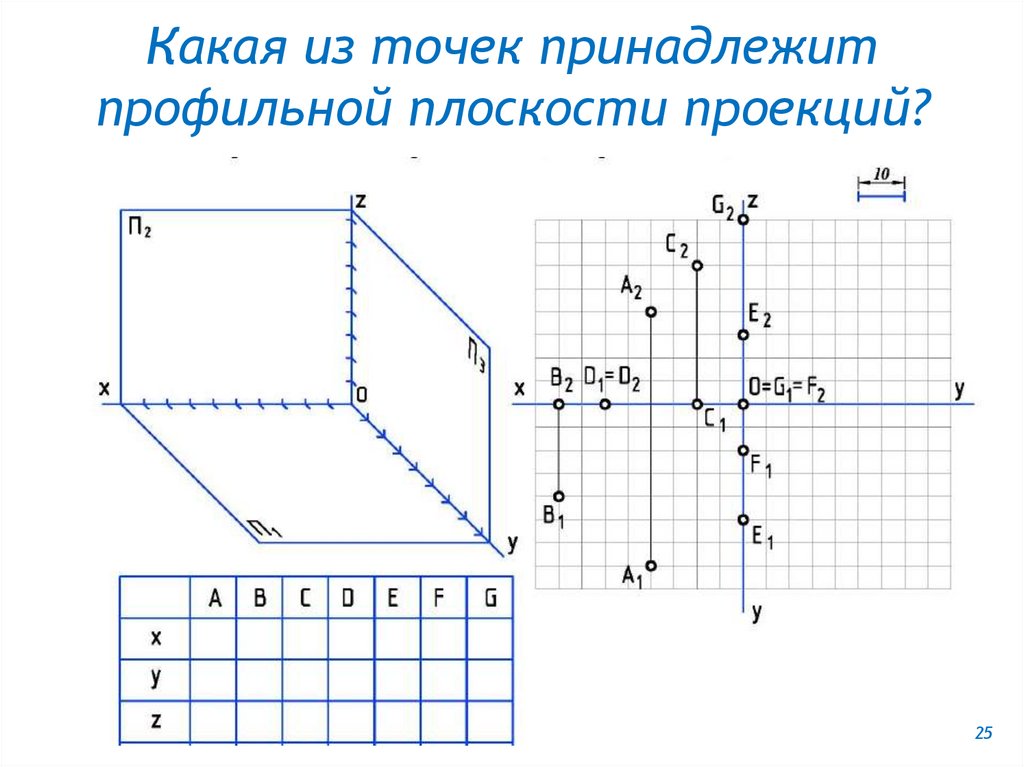
Какая из точек принадлежит
профильной плоскости проекций?
25

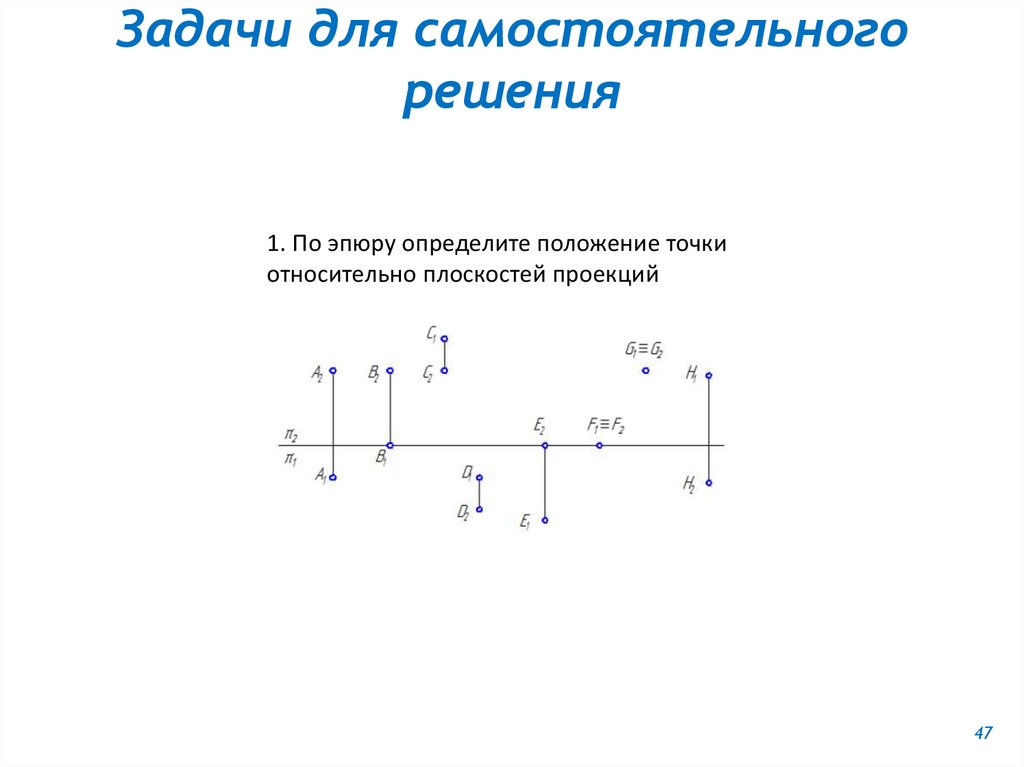
23.

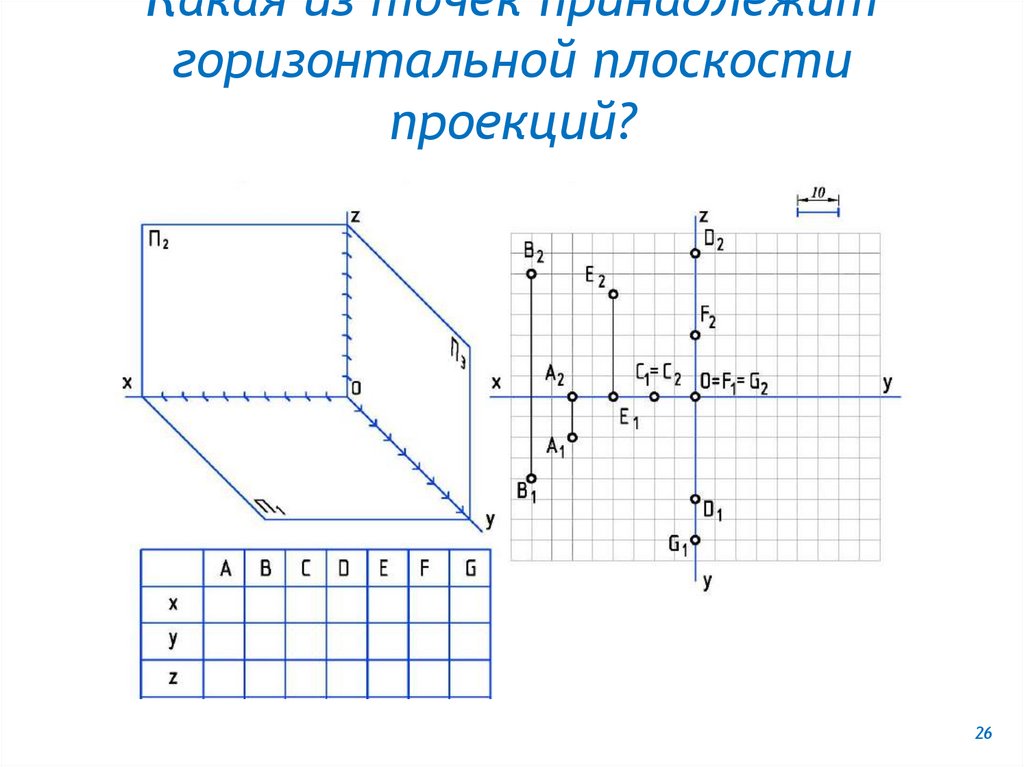
Какая из точек принадлежит
горизонтальной плоскости
проекций?
26

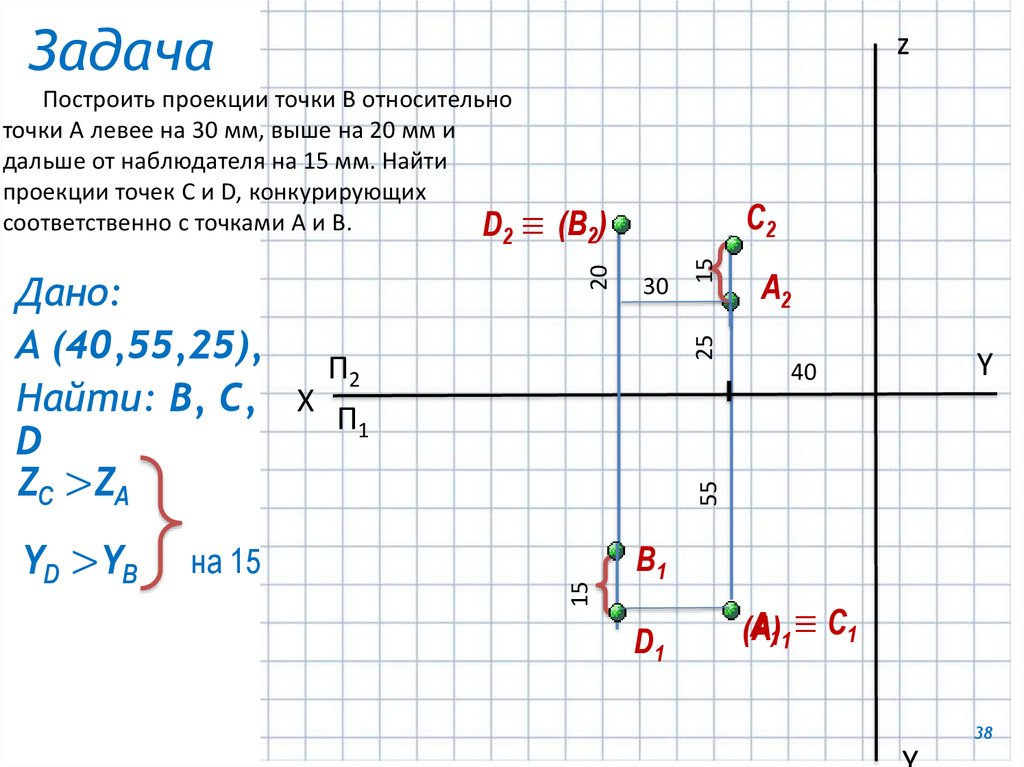
24.

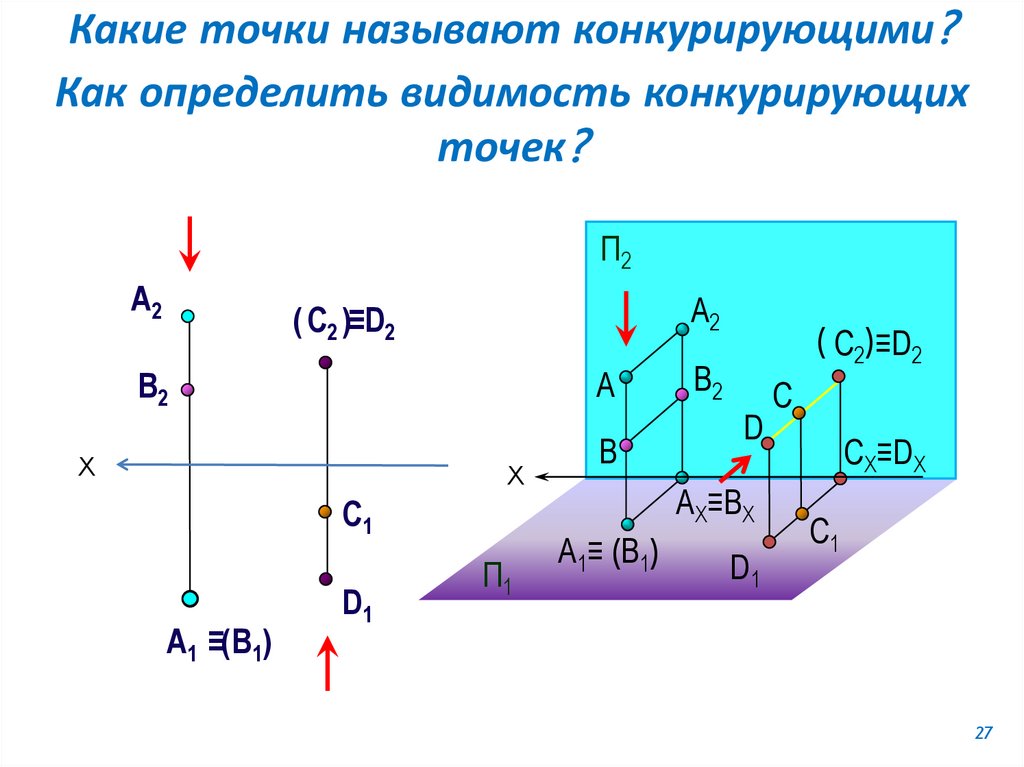
Какие точки называют конкурирующими?
Как определить видимость конкурирующих
точек?
П2
А2
А2
( C2 )≡D2
А
В2
X
X
С1
А1 ≡( В1)
D1
П1
В
( C2)≡D2
В2
D
АХ≡ВХ
А1≡ (В1)
D1
С
CХ≡DХ
С1
27

25.

РЕШАЕМ ЗАДАЧИ ПО ТЕМЕ:
ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ТОЧКИ
31

26.

Задача 3
YA
z
А2
А3
Дано:
XA
П2
X
П1
0
Y
YA
• А (45, 40,
65)
• В (60, 35, 0)
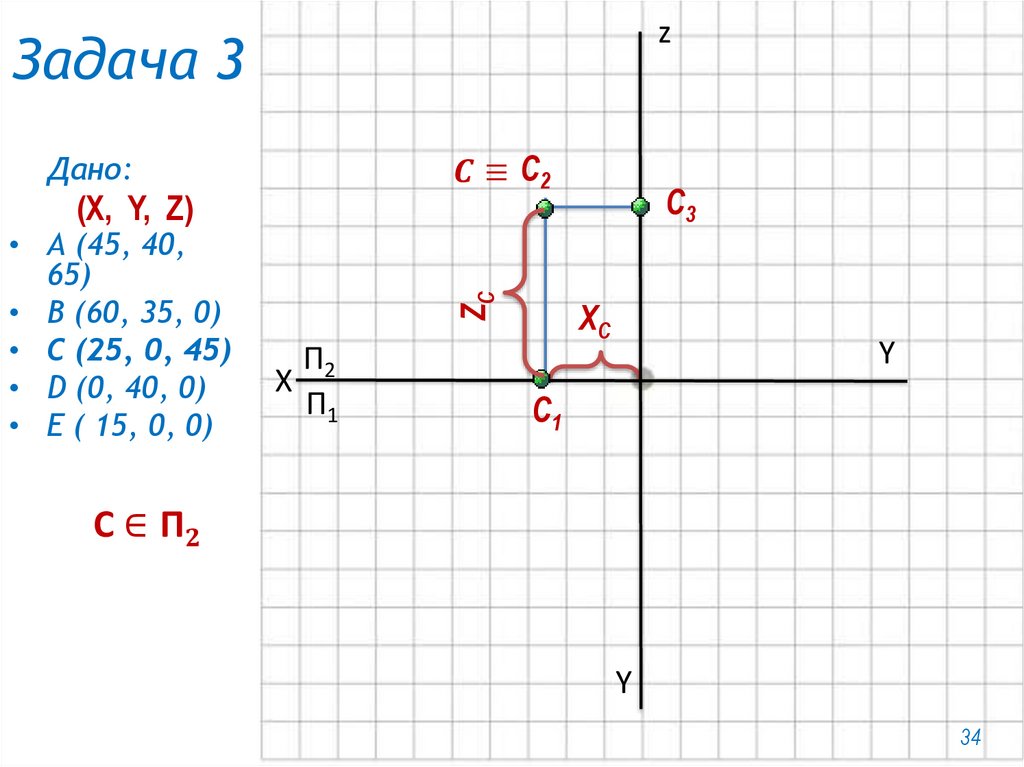
• С (25, 0, 45)
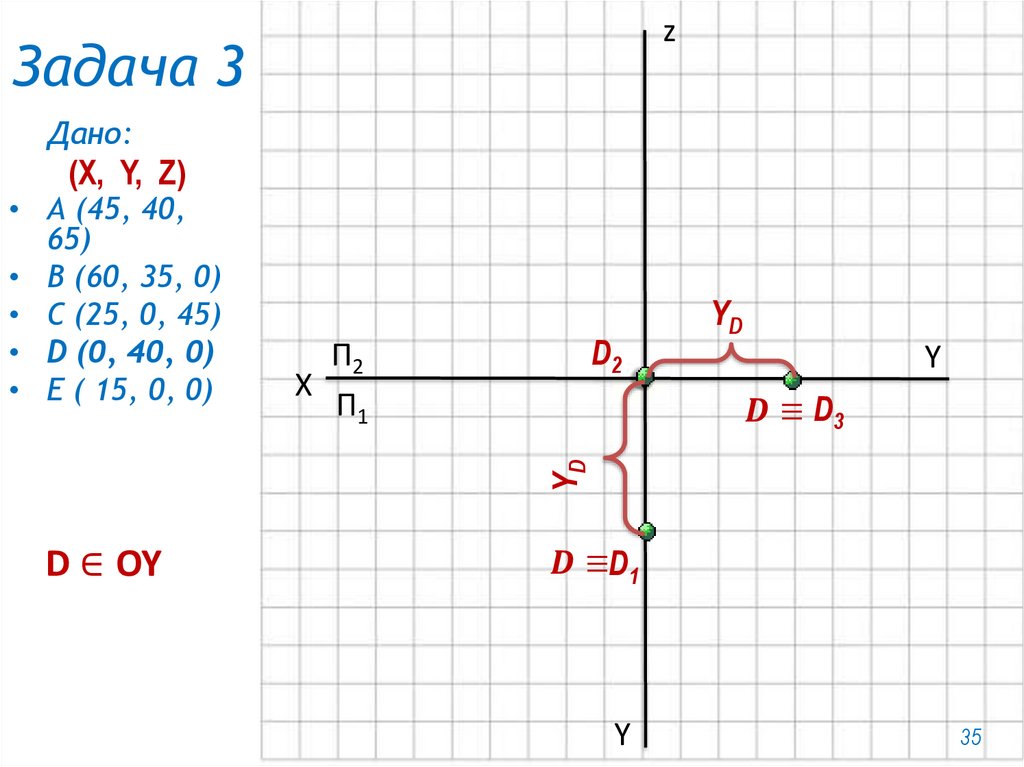
• D (0, 40, 0)
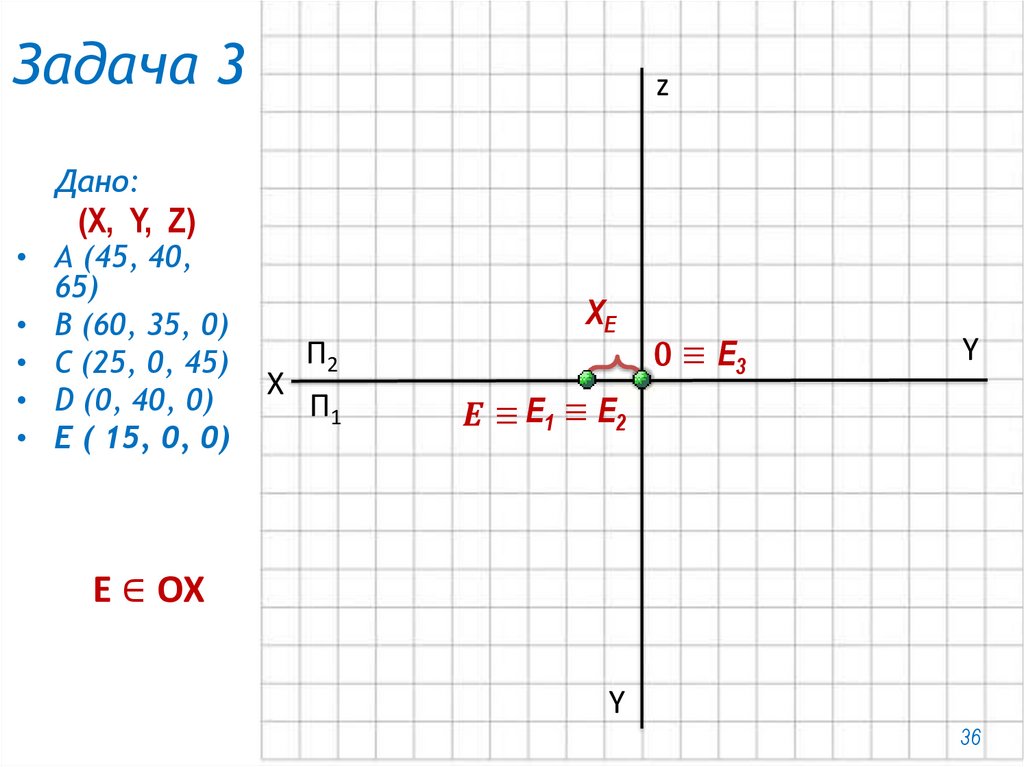
• E ( 15, 0, 0)
ZA
(X, Y, Z)
А1
Y
32

27.

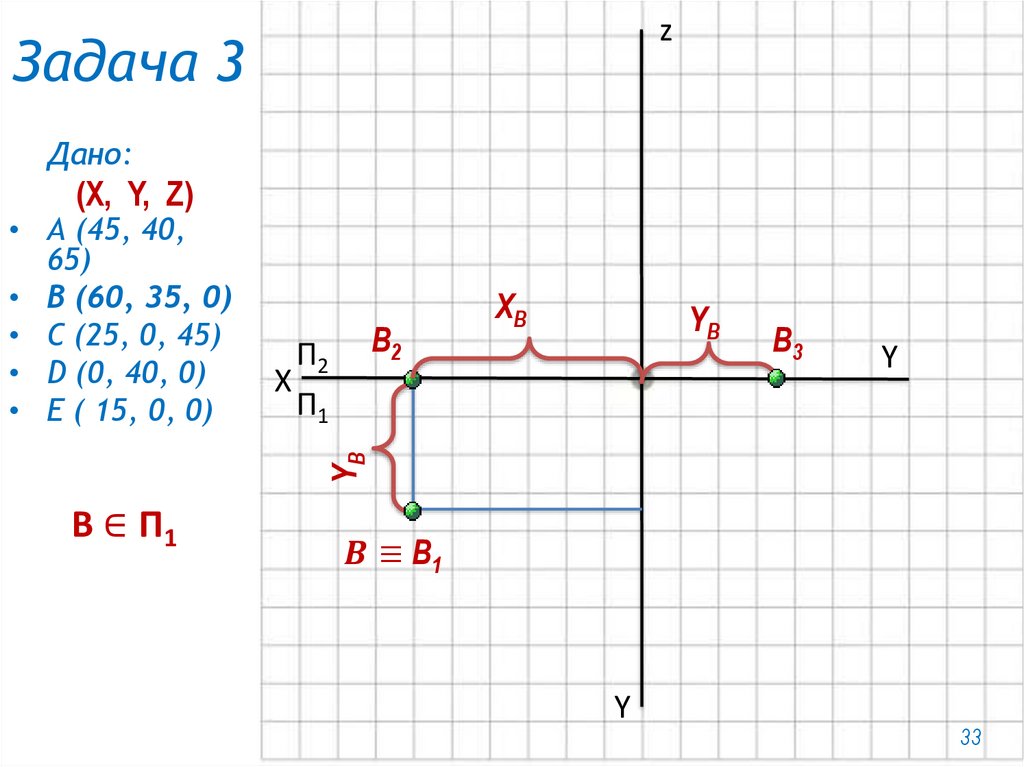
z
Задача 3
Дано:
(X, Y, Z)
B2
П2
X
П1
XB
YB
B3
Y
YB
• А (45, 40,
65)
• В (60, 35, 0)
• С (25, 0, 45)
• D (0, 40, 0)
• E ( 15, 0, 0)
В ∈ П1