Similar presentations:
Метод проекций. Проекция точки
1. Тема 1
Пермский государственный технический университетКафедра дизайна, графики и начертательной
геометрии
Е.С. Дударь, И.Д. Столбова
Тема 1
Метод проекций. Проекция точки
Цель: сформировать представление о
конструктивном способе отображения пространства
2.
Метод проекцийПространство
расширенное евклидово
Способ
конструктивный (проецирование)
отображения
пространства
нелинейные:
Геометрические линейные (неопределяемые):
• точка;
образы:
• кривая линия;
• прямая;
• поверхность
• плоскость
• наглядность;
• простота;
Требования к
• точность;
• обратимость
чертежу
построить проекционный чертеж
Прямая задача
пространственного предмета
прочитать чертеж, т.е. реконструировать натуОбратная
ральные пространственные формы, размеры и
задача
положение изображаемого предмета
Основной метод начертательной геометрии. Используется для
построения изображения геометрических образов трехмерного
пространства на плоскости чертежа
3.
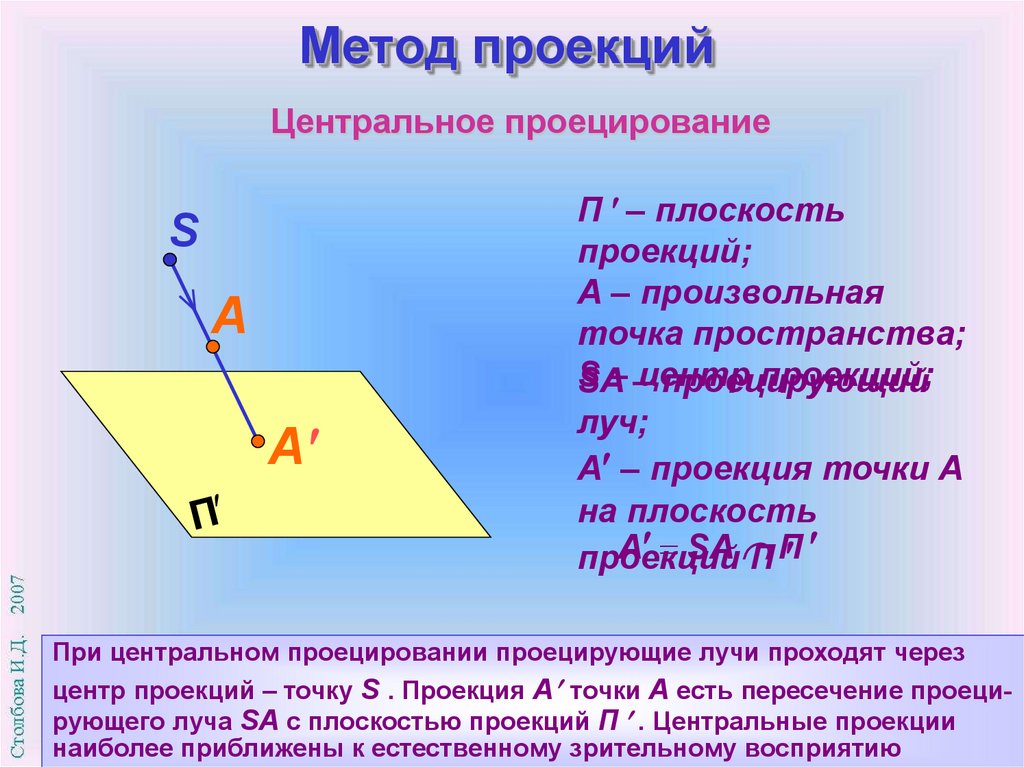
Метод проекцийЦентральное проецирование
S
A
А
П – плоскость
проекций;
А – произвольная
точка пространства;
S
проекций;
SA– –центр
проецирующий
луч;
А – проекция точки А
на плоскость
А = SA
проекций
ПП
При центральном проецировании проецирующие лучи проходят через
центр проекций – точку S . Проекция А точки А есть пересечение проецирующего луча SA с плоскостью проекций П . Центральные проекции
наиболее приближены к естественному зрительному восприятию
4.
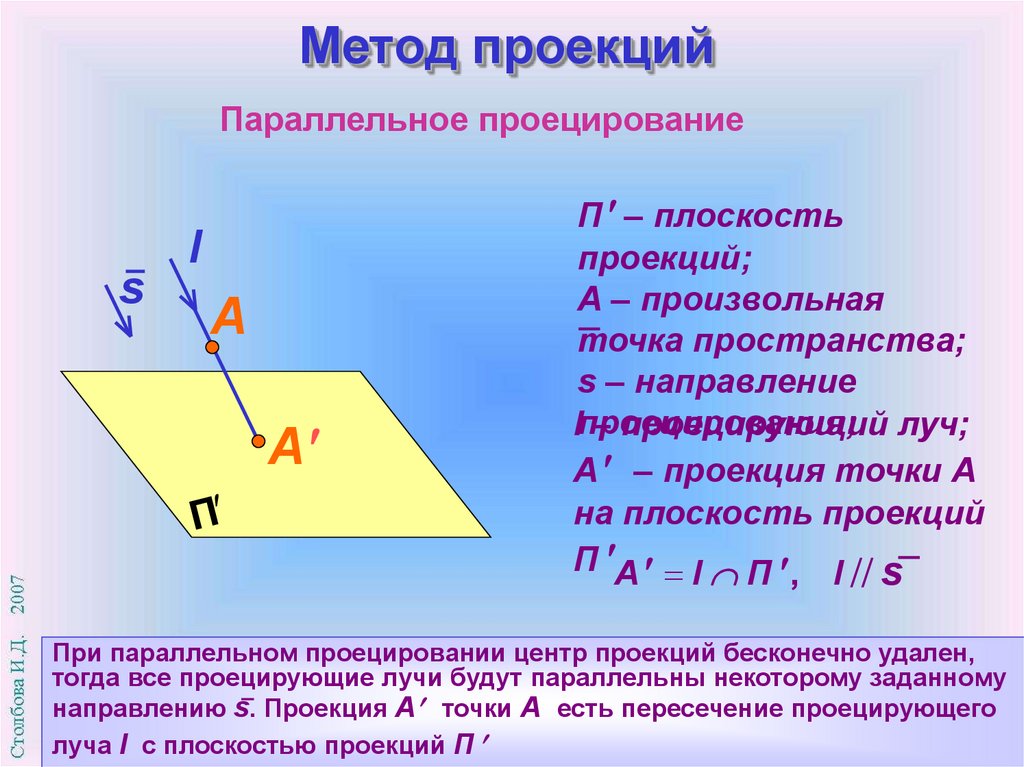
Метод проекцийПараллельное проецирование
s
l
A
А
П – плоскость
проекций;
А – произвольная
точка пространства;
s – направление
lпроецирования;
– проецирующий луч;
А – проекция точки А
на плоскость проекций
П А = l П , l s
При параллельном проецировании центр проекций бесконечно удален,
тогда все проецирующие лучи будут параллельны некоторому заданному
направлению s. Проекция A точки А есть пересечение проецирующего
луча l с плоскостью проекций П
5.
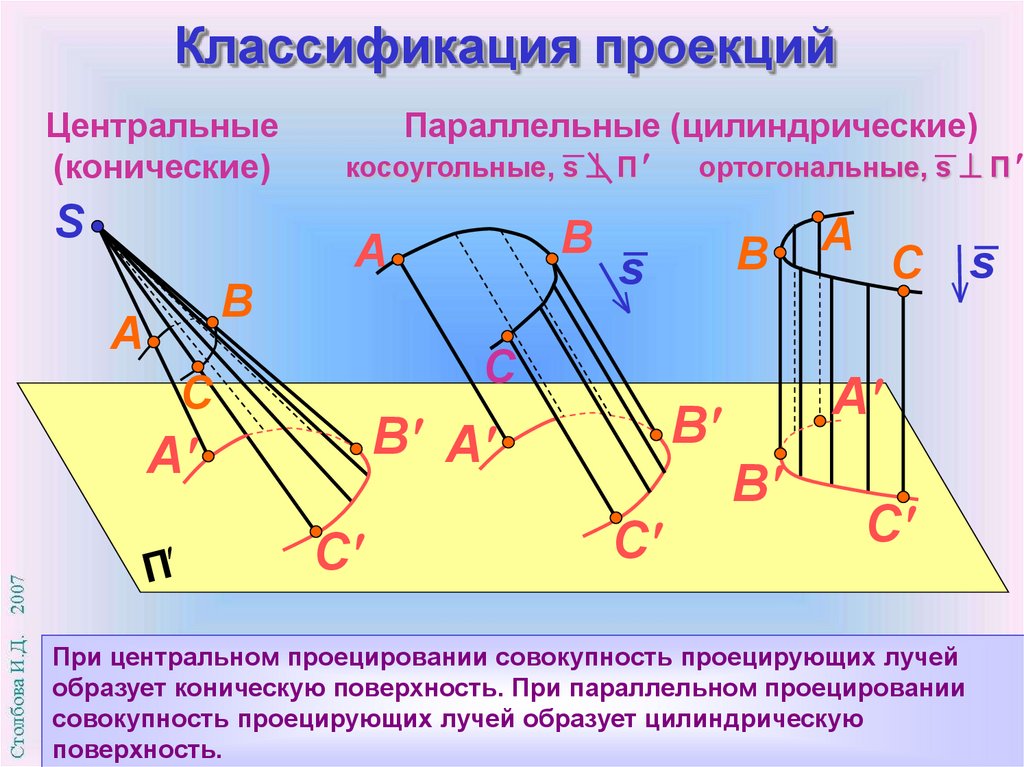
Классификация проекцийЦентральные
(конические)
S
Параллельные (цилиндрические)
косоугольные, s П
ортогональные, s П
B
A
B
A
B
s
C
C
А
С
С
C
А
В
В А
A
В
С
При центральном проецировании совокупность проецирующих лучей
образует коническую поверхность. При параллельном проецировании
совокупность проецирующих лучей образует цилиндрическую
поверхность.
s
6.
Общие свойства центрального ипараллельного проецирования
• Проекция точки есть точка
• Проекция прямой линии, в общем случае,
прямая
• Каждая точка и линия в пространстве имеют
свою единственную проекцию
• Если точка принадлежит прямой, то и
проекция точки принадлежит проекции
данной прямой
• Для построения проекции прямой
достаточно спроецировать две ее точки и
через полученные проекции этих точек
провести прямую линию
7.
Свойства параллельногопроецирования
• Отношение длин отрезков прямой равно
отношению длин их проекций
• Отрезок прямой, параллельный плоскости
проекций, проецируется на эту плоскость без
искажения
• Проекции параллельных прямых
параллельны
• Отношение длин отрезков параллельных
прямых равно отношению длин их проекций
• При параллельном переносе плоскости
проекций величина проекций не меняется
8.
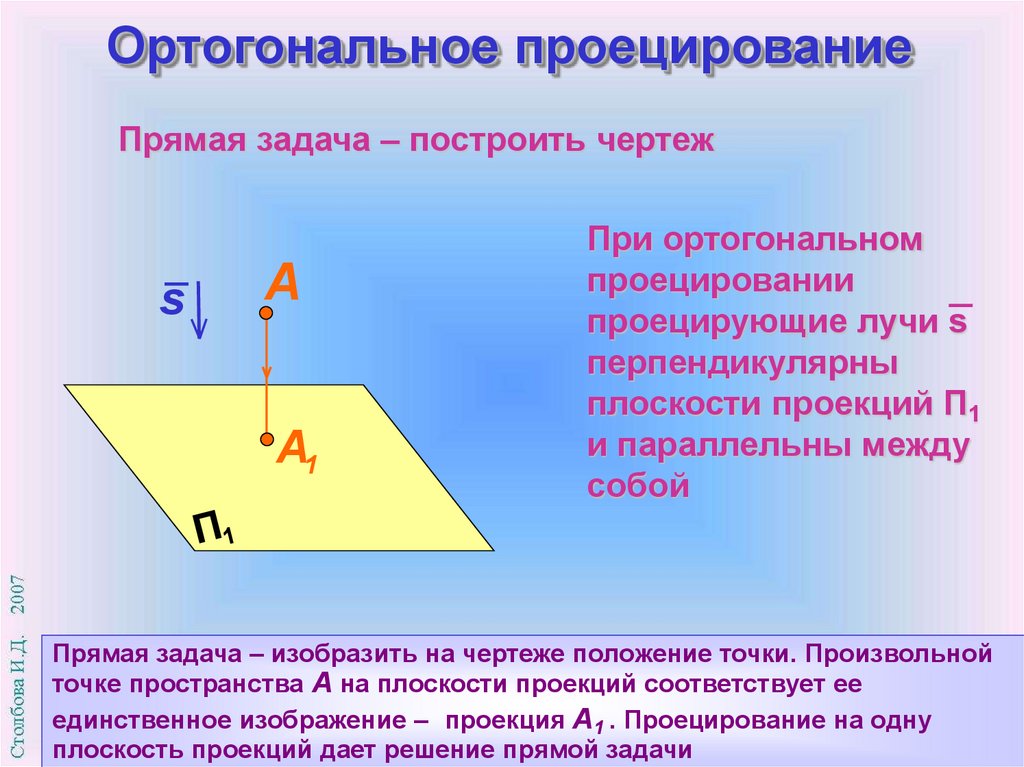
Ортогональное проецированиеПрямая задача – построить чертеж
s
A
А1
При ортогональном
проецировании
проецирующие лучи s
перпендикулярны
плоскости проекций П1
и параллельны между
собой
Прямая задача – изобразить на чертеже положение точки. Произвольной
точке пространства А на плоскости проекций соответствует ее
единственное изображение – проекция А1 . Проецирование на одну
плоскость проекций дает решение прямой задачи
9.
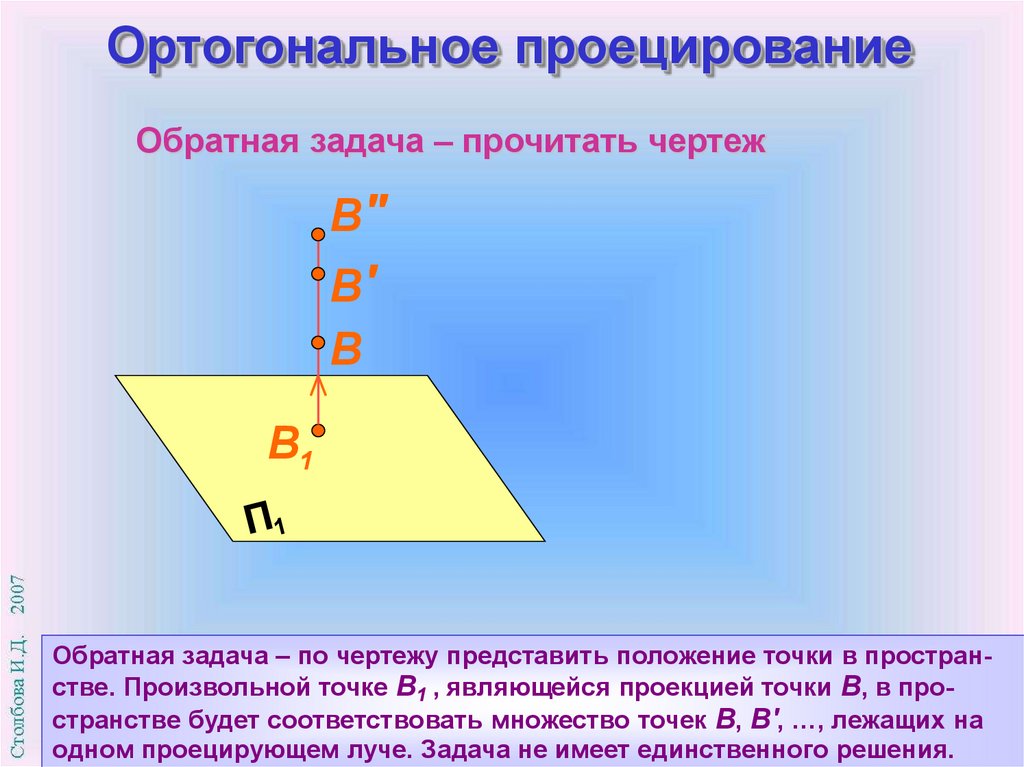
Ортогональное проецированиеОбратная задача – прочитать чертеж
В"
В'
В
В1
Обратная задача – по чертежу представить положение точки в пространстве. Произвольной точке В1 , являющейся проекцией точки В, в пространстве будет соответствовать множество точек В, В', …, лежащих на
одном проецирующем луче. Задача не имеет единственного решения.
10.
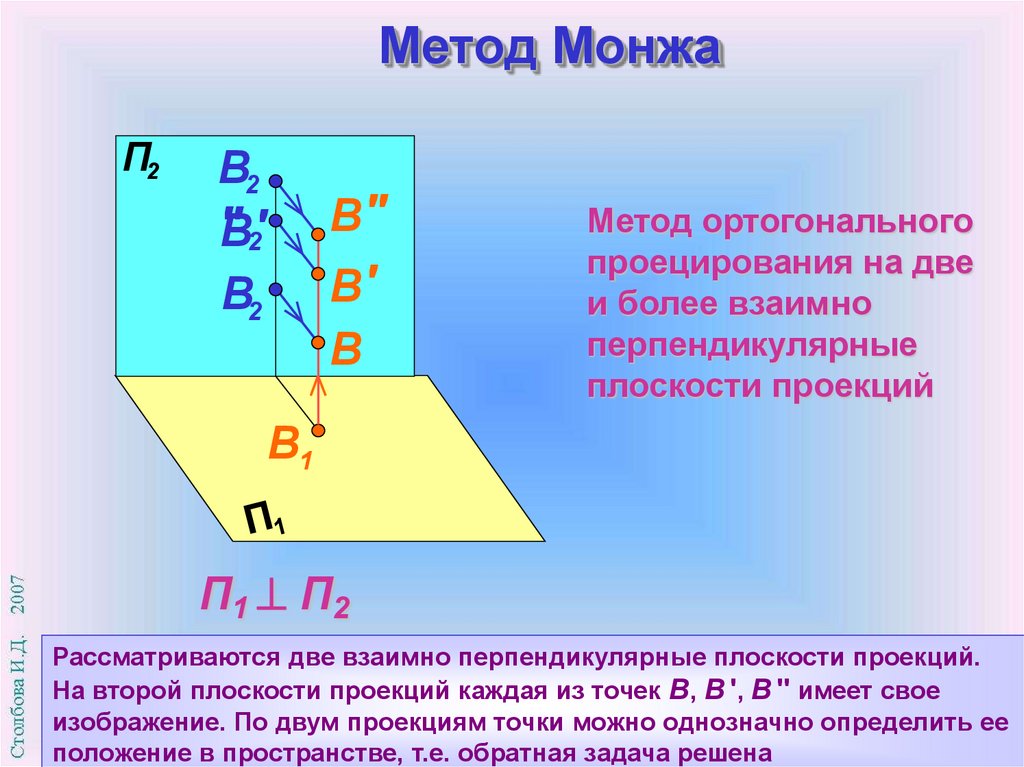
Метод МонжаП2
В2
"В2'
В2
В"
В'
В
Метод ортогонального
проецирования на две
и более взаимно
перпендикулярные
плоскости проекций
В1
П1 П2
Рассматриваются две взаимно перпендикулярные плоскости проекций.
На второй плоскости проекций каждая из точек В, В ', В " имеет свое
изображение. По двум проекциям точки можно однозначно определить ее
положение в пространстве, т.е. обратная задача решена
11.
Метод МонжаМетод ортогонального проецирования:
• плоскости проекций перпендикулярны
между собой;
• проецирующие лучи перпендикулярны
плоскости проекций.
Для однозначного определения положения точки
в пространстве необходимо задать на чертеже
минимум две ее ортогональные проекции
Комплексный чертеж – это изображение
геометрического образа, полученное при
совмещенных плоскостях проекций
12.
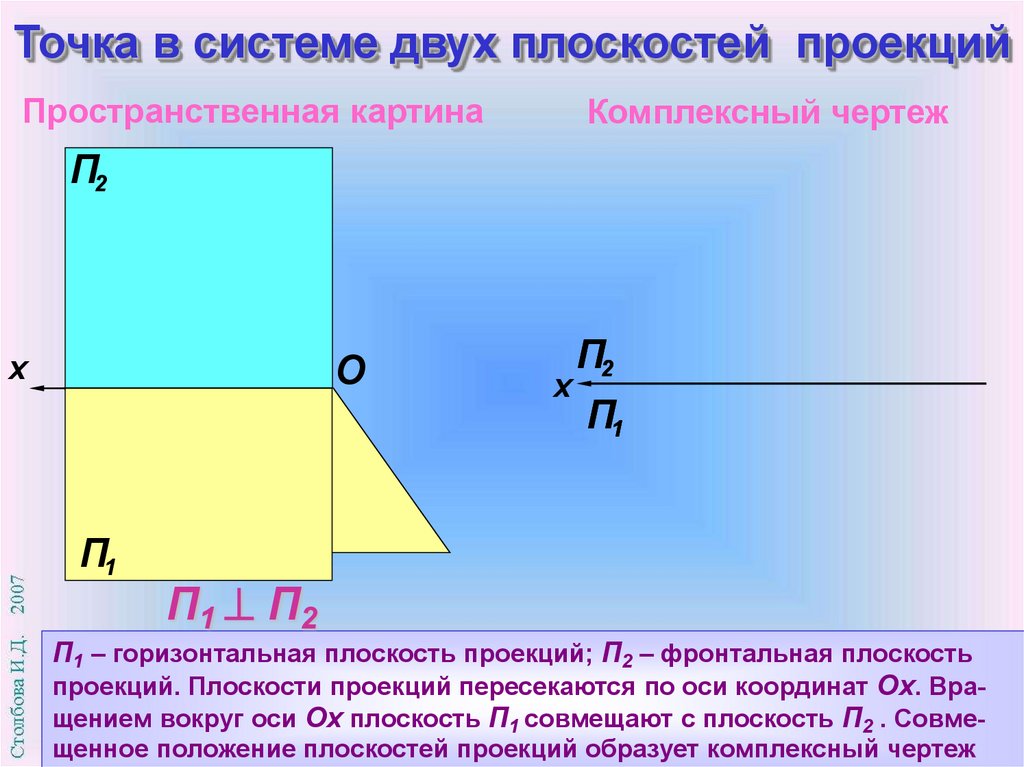
Точка в системе двух плоскостей проекцийПространственная картина
Комплексный чертеж
П2
x
O
П1
x
П2
П1
П1 П2
П1 – горизонтальная плоскость проекций; П2 – фронтальная плоскость
проекций. Плоскости проекций пересекаются по оси координат Оx. Вращением вокруг оси Ох плоскость П1 совмещают с плоскость П2 . Совмещенное положение плоскостей проекций образует комплексный чертеж
13.
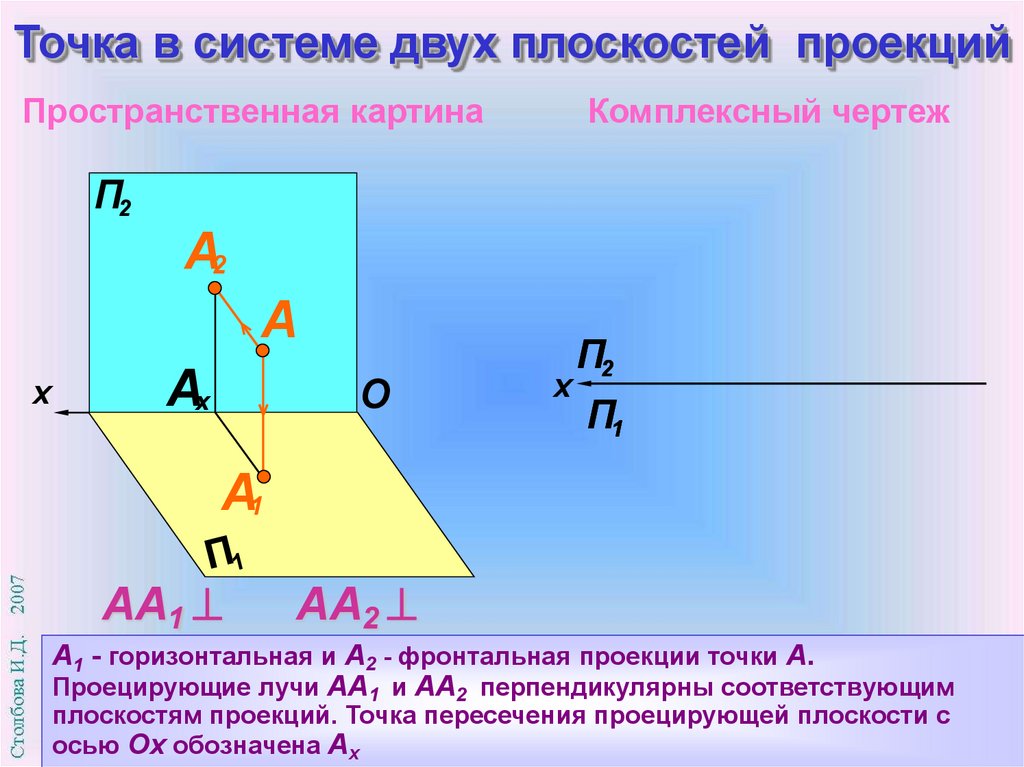
Точка в системе двух плоскостей проекцийПространственная картина
Комплексный чертеж
П2
А2
A
x
Аx
x
O
П2
П1
А1
АА1
АА2
А1 - П
горизонтальная
и А2 - фронтальная проекции точки А.
;
П
1
2
Проецирующие лучи АА
и АА перпендикулярны соответствующим
1
2
плоскостям проекций. Точка пересечения проецирующей плоскости с
осью Оx обозначена Ах
14.
Точка в системе двух плоскостей проекцийПространственная картина
Комплексный чертеж
П2
А2
А2
A
Аx
x
П1
А1
O
А1
x
Аx
А1
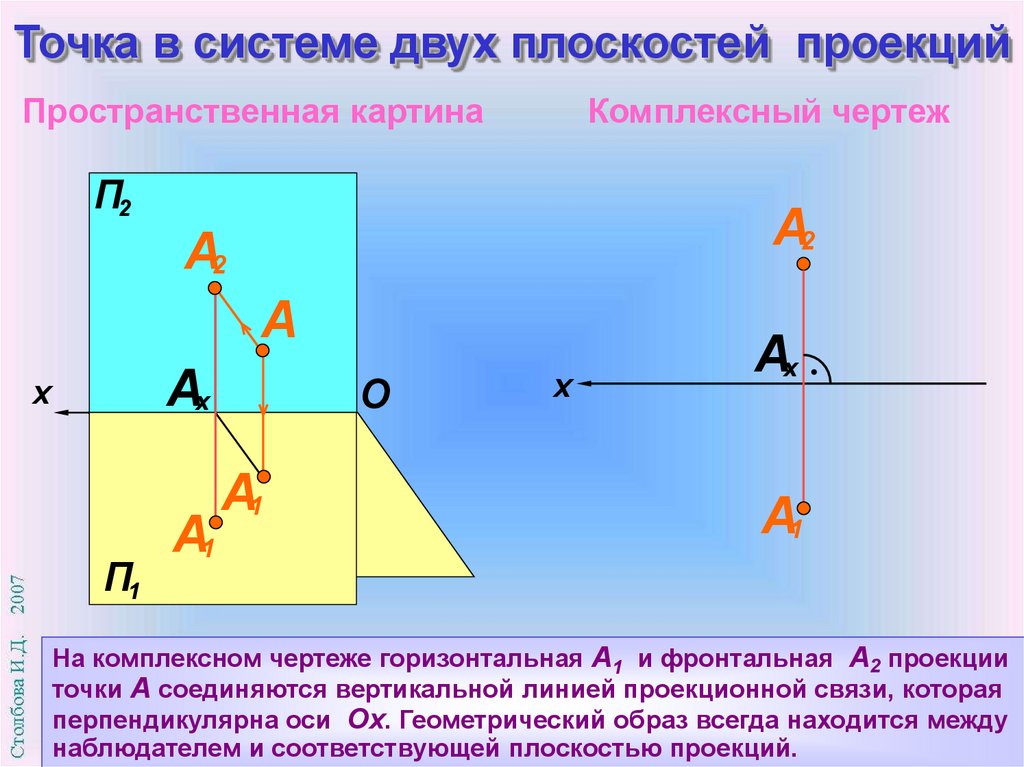
На комплексном чертеже горизонтальная А1 и фронтальная А2 проекции
точки А соединяются вертикальной линией проекционной связи, которая
перпендикулярна оси Ох. Геометрический образ всегда находится между
наблюдателем и соответствующей плоскостью проекций.
15.
Точка в системе трех плоскостей проекцийПространственная картина
z
П2
x
O
П1 П2 П3
y
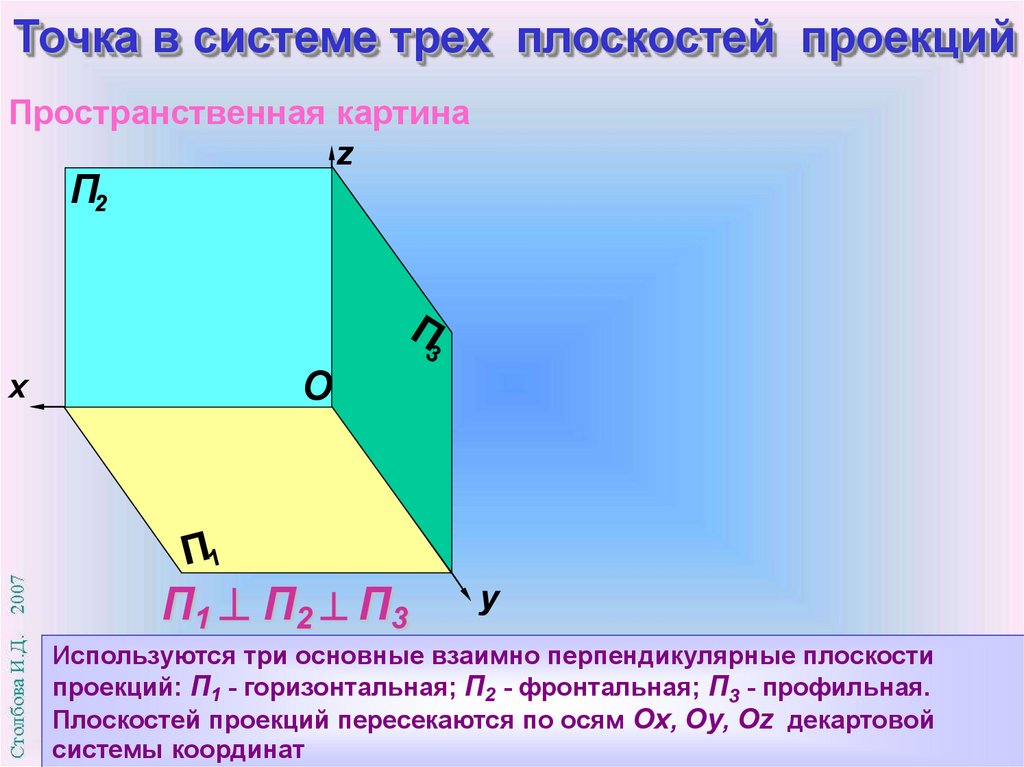
Используются три основные взаимно перпендикулярные плоскости
проекций: П1 - горизонтальная; П2 - фронтальная; П3 - профильная.
Плоскостей проекций пересекаются по осям Оx, Оy, Оz декартовой
системы координат
16.
Точка в системе трех плоскостей проекцийПространственная картина
z
Комплексный чертеж
П2
П2
O
x
z
П3
y3 x
П1
П1
y1
y
O
П3
y3
y1
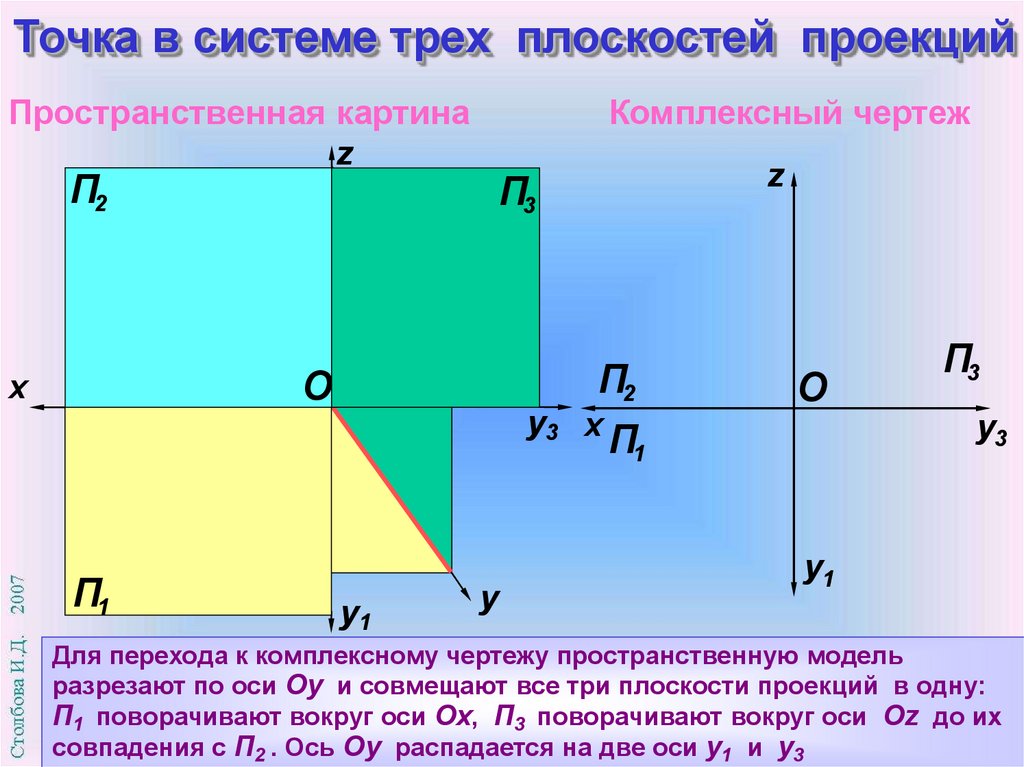
Для перехода к комплексному чертежу пространственную модель
разрезают по оси Оy и совмещают все три плоскости проекций в одну:
П1 поворачивают вокруг оси Оx, П3 поворачивают вокруг оси Оz до их
совпадения с П2 . Ось Оу распадается на две оси y1 и y3
17.
Точка в системе трех плоскостей проекцийПространственная картина
z
П2
А2
Комплексный чертеж
z
Аz
A
x
Аx
O
А1
А3
Аy
П2
O
xП
П3
y3
1
y1
АА1 П1АА
; 2 П2 АА3 П3y
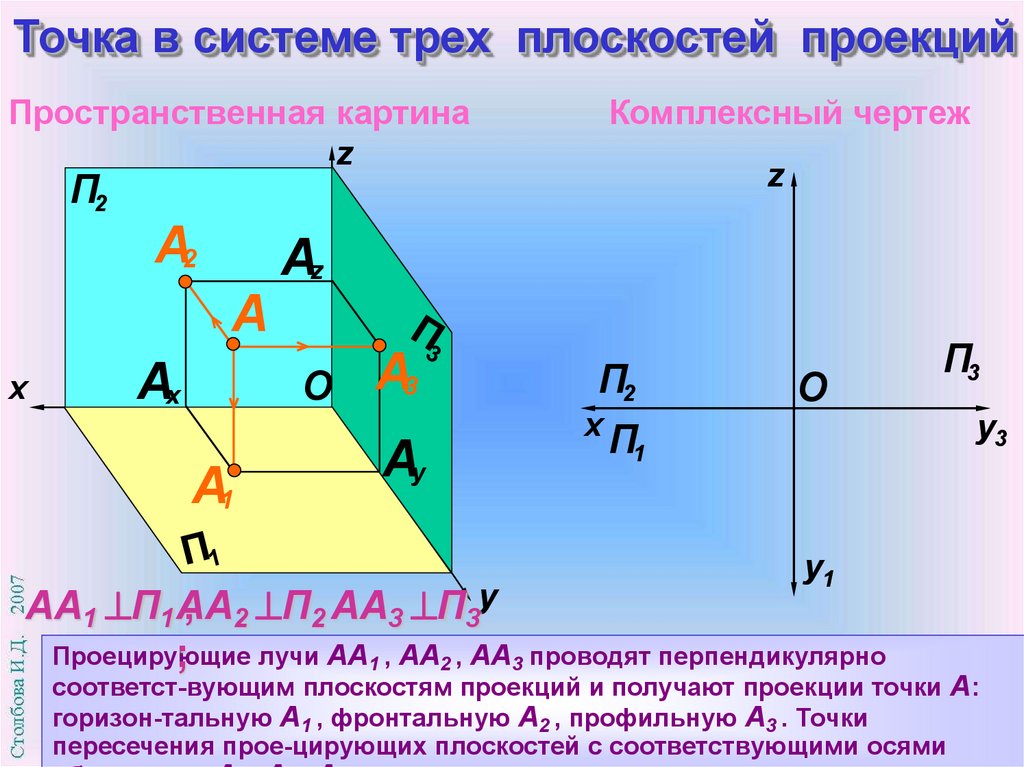
Проецирующие
лучи АА1 , АА2 , АА3 проводят перпендикулярно
;
соответст-вующим плоскостям проекций и получают проекции точки А:
горизон-тальную А1 , фронтальную А2 , профильную А3 . Точки
пересечения прое-цирующих плоскостей с соответствующими осями
18.
Точка в системе трех плоскостей проекцийПространственная картина
z
Комплексный чертеж
П2
А2
Аz
А3
A
Аx
x
А1
П1
z
П3
А3
O
y3
Аy
А1
y1
y
x
А2
Аz
А3
Аx
O
Аy
3
y3
А1 Аy
1
y1
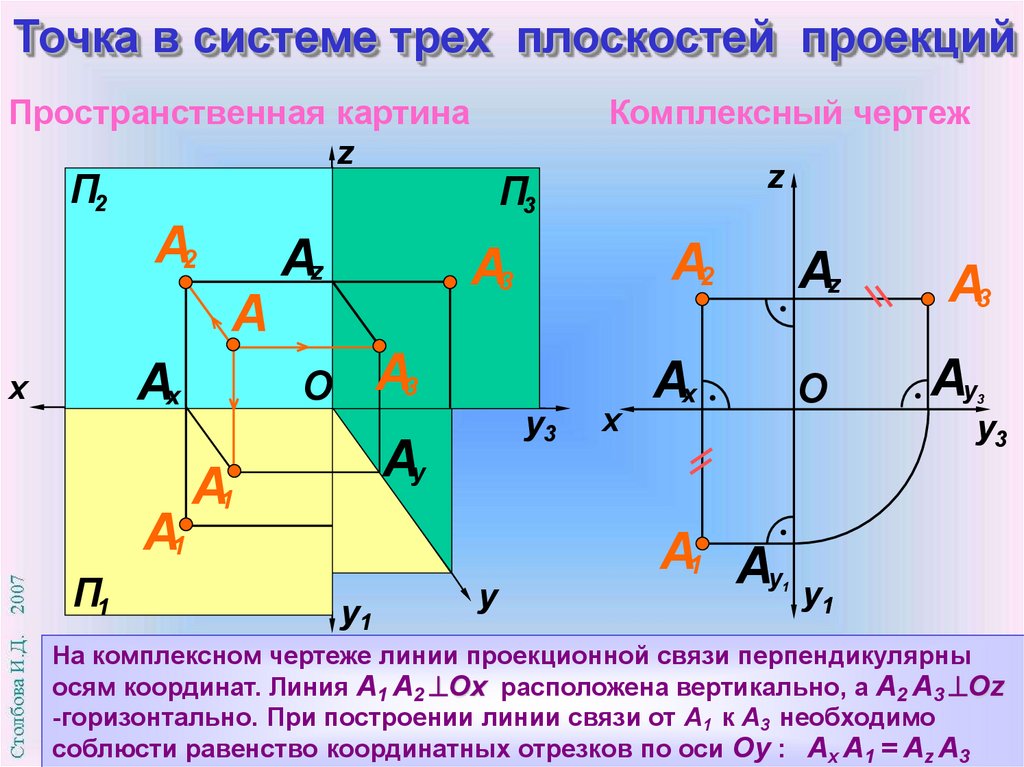
На комплексном чертеже линии проекционной связи перпендикулярны
осям координат. Линия А1 А2 Ох расположена вертикально, а А2 А3 Оz
-горизонтально. При построении линии связи от А1 к А3 необходимо
соблюсти равенство координатных отрезков по оси Оy : Ax A1 = Az A3
19. Безосный чертеж
П2П2
А2
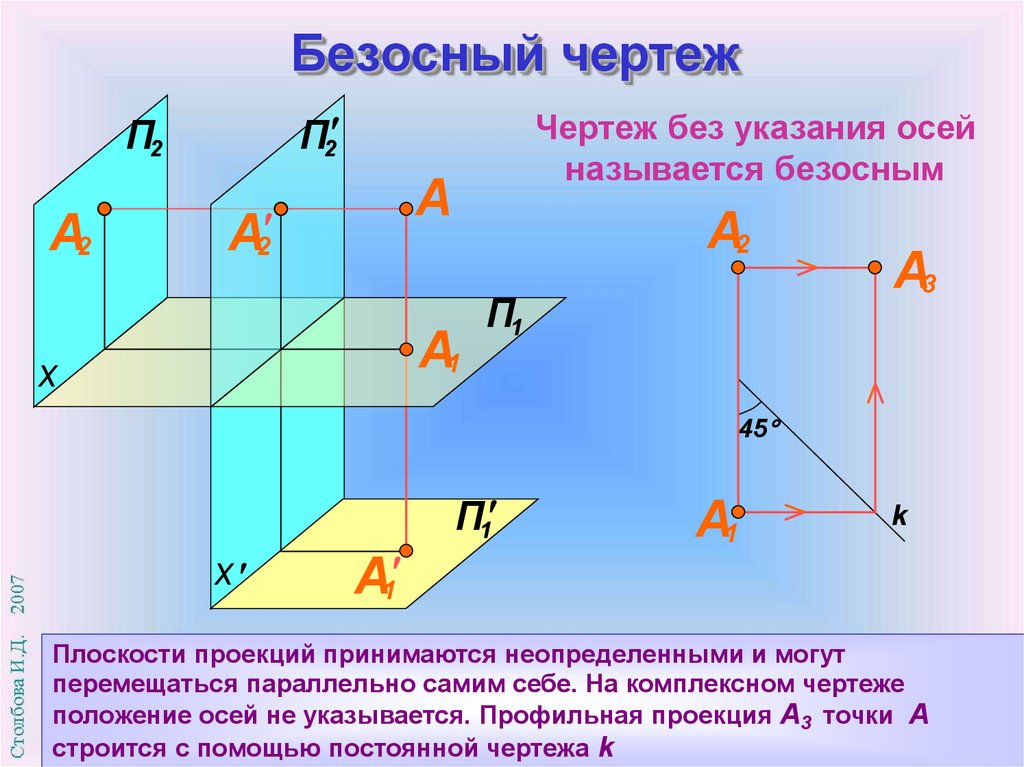
Чертеж без указания осей
называется безосным
А
А2
А2
А1
x
П1
А3
45
П1
x
А1
А1
k
Плоскости проекций принимаются неопределенными и могут
перемещаться параллельно самим себе. На комплексном чертеже
положение осей не указывается. Профильная проекция А3 точки А
строится с помощью постоянной чертежа k
20.
Прямоугольные координаты точкиz
П2
А2
y
x
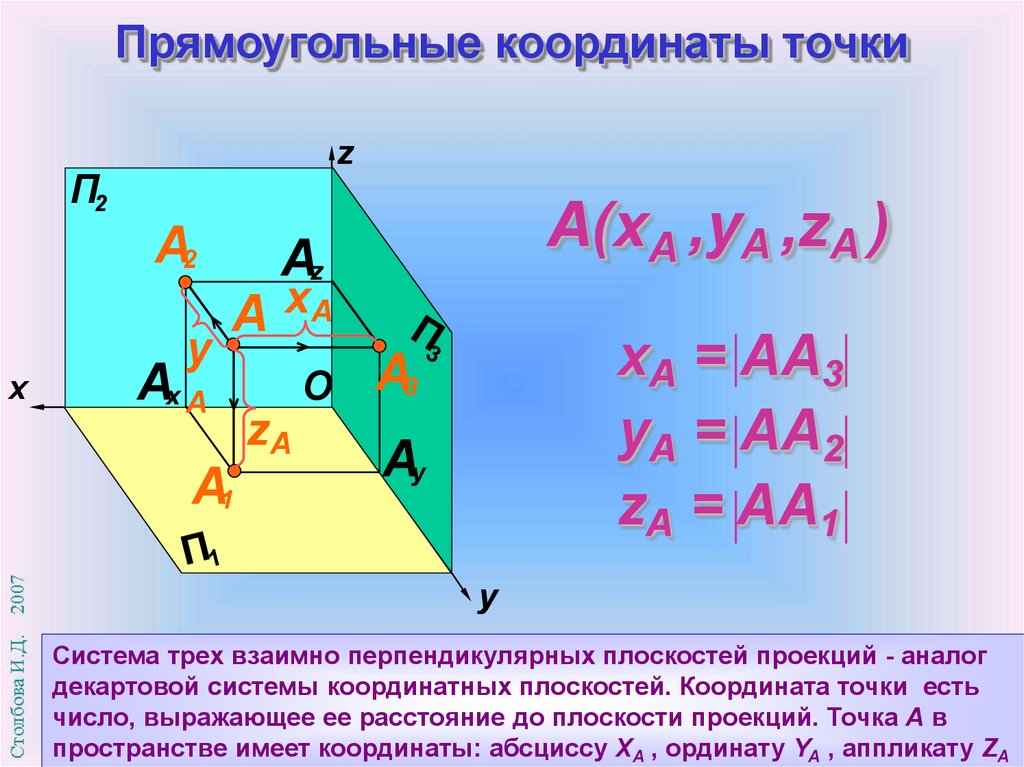
A(xA ,yA ,zA )
Аz
A xA
Аx A
А1
O
zA
xA = AA3
yA = AA2
zA = AA1
А3
Аy
y
Система трех взаимно перпендикулярных плоскостей проекций - аналог
декартовой системы координатных плоскостей. Координата точки есть
число, выражающее ее расстояние до плоскости проекций. Точка А в
пространстве имеет координаты: абсциссу XA , ординату YA , аппликату ZA
21.
Прямоугольные координаты точкиz
А2
y
А2
zA
A
zA
O
O
x
x
xA
y
A
А1
xA
y
A
А1
А3
zA
y3
y1
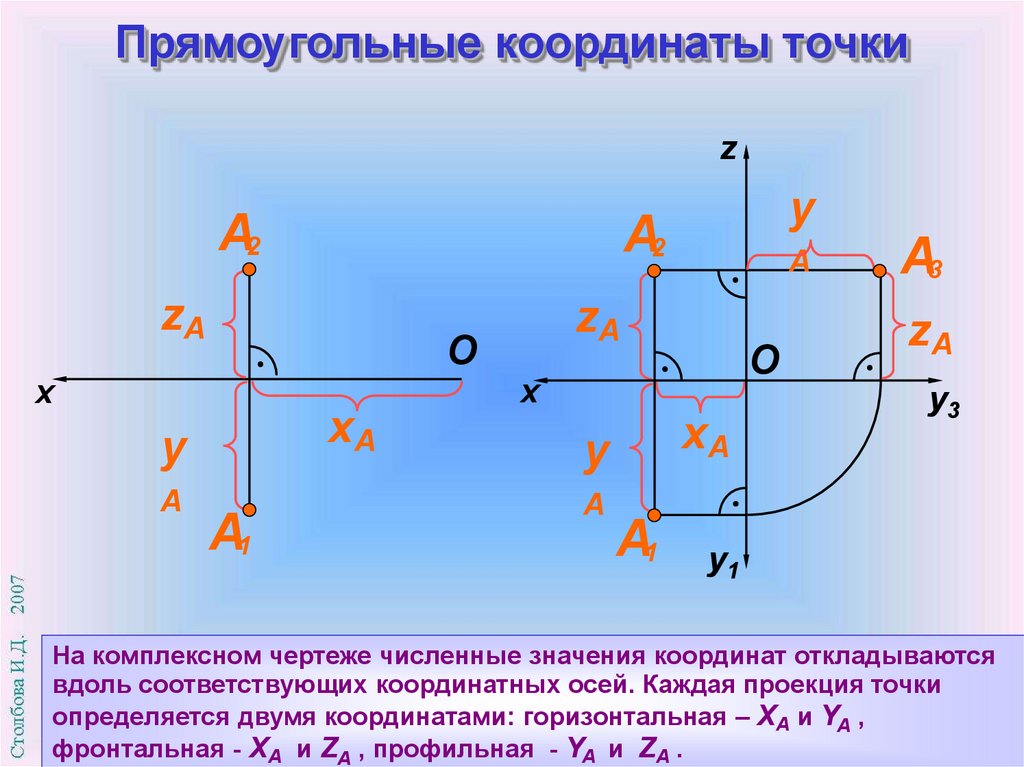
На комплексном чертеже численные значения координат откладываются
вдоль соответствующих координатных осей. Каждая проекция точки
определяется двумя координатами: горизонтальная – XA и YA ,
фронтальная - XA и ZA , профильная - YA и ZA .
22.
Конкурирующие точкиКонкурирующими называются точки, лежащие на
одном проецирующем луче.
П2
В2
A2
B2
А2
В
z
A
В1 (A1)
zB > zA
z
x
В1 (A1)
Горизонтально конкурирующие точки А и В лежат на общем
горизонтально-проецирующем луче, поэтому их горизонтальные
проекции совпадают. Точка В выше точки А и расположена ближе к
наблюдателю, ее горизонтальная проекция В1 будет видимой
23.
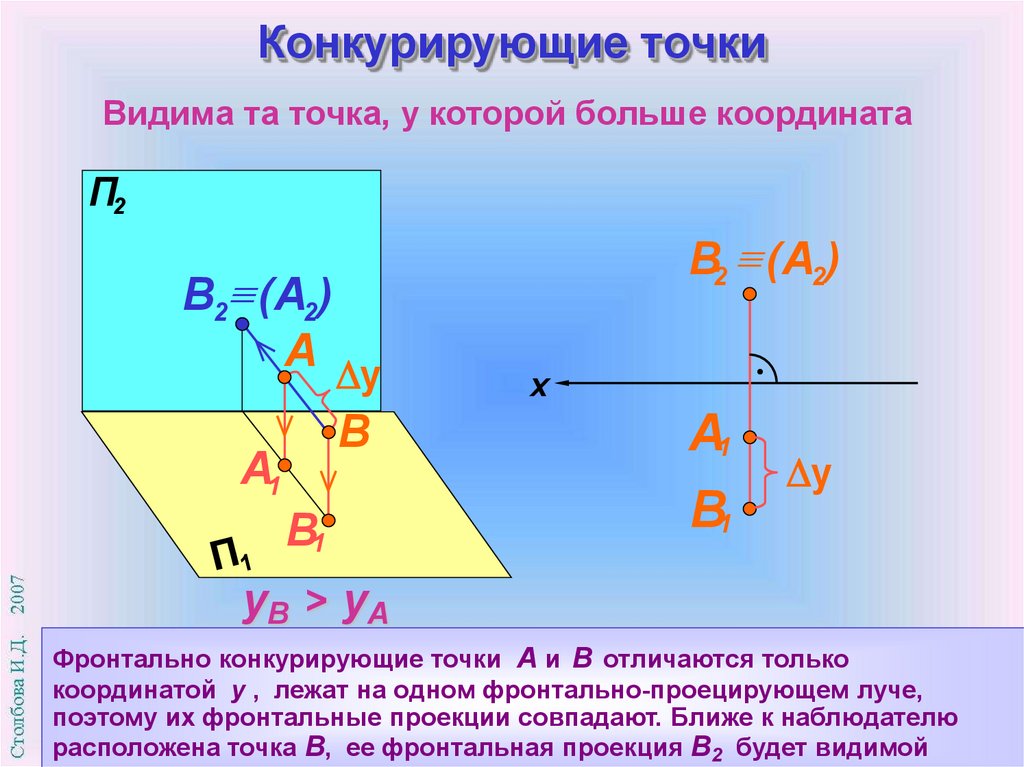
Конкурирующие точкиВидима та точка, у которой больше координата
П2
В2 (A2)
A y
В
A1
В1
В2 (A2)
x
А1
B1
y
yB > yA
Фронтально конкурирующие точки А и В отличаются только
координатой y , лежат на одном фронтально-проецирующем луче,
поэтому их фронтальные проекции совпадают. Ближе к наблюдателю
расположена точка В, ее фронтальная проекция В2 будет видимой






 drafting
drafting








