Метод проекций. Начертательная геометрия

1.

Метод
проекций
Эпюр
Монжа

2.

Начертательная геометрия
является тем разделом геометрии,
в котором изучаются методы
изображения пространственных
фигур на чертеже и алгоритмы
решения позиционных,
метрических и конструкционных
задач
Начертательная геометрия… « является наивысшим
средством для развития той таинственной и мало
поддающейся изучению точными науками способности
человеческого духа,
которая зовется воображением и которая является
ступенью к другой способности – фантазии, без которой
не совершаются великие открытия и изобретения»
Н. А. Рынин

3.

Как сформировавшаяся наука
начертательная геометрия
(метод ортогонального проецирования)
возникла лишь в результате трудов
французского ученого и общественного
деятеля
Гаспара Монжа,
который свел в стройную систему весь
разрозненный материал по методу
ортогонального проецирования,
и по заслугам считается его творцом
http://im3-tub.yandex.net/i?id=30705874-07-24
Гаспар Монж
(1746 1818)
Он впервые предложил рассматривать плоский чертеж из
двух проекций как результат совмещения двух плоскостей
проекций вращением вокруг их общей линии, названной
осью проекций

4.

МЕТОДЫ
ПРОЕЦИРОВАНИЯ

5.

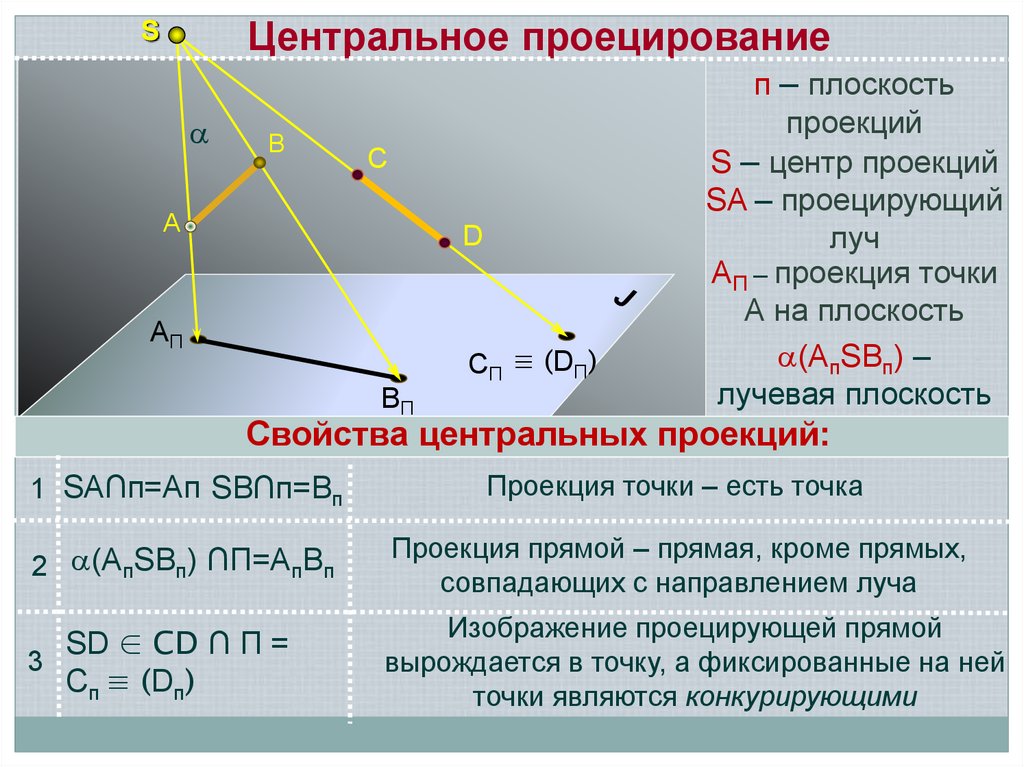
Центральное проецирование
S
В
C
А
D
AП
CП ≡ (DП)
BП
п – плоскость
проекций
S – центр проекций
SA – проецирующий
луч
AП – проекция точки
А на плоскость
(AпSBп) –
лучевая плоскость
Свойства центральных проекций:
1 SA∩п=Aп SB∩п=Bп
Проекция точки – есть точка
2 (AпSBп) ∩П=AпBп
Проекция прямой – прямая, кроме прямых,
совпадающих с направлением луча
SD ∈ CD ∩ П =
3
Сп ≡ (Dп)
Изображение проецирующей прямой
вырождается в точку, а фиксированные на ней
точки являются конкурирующими

6.

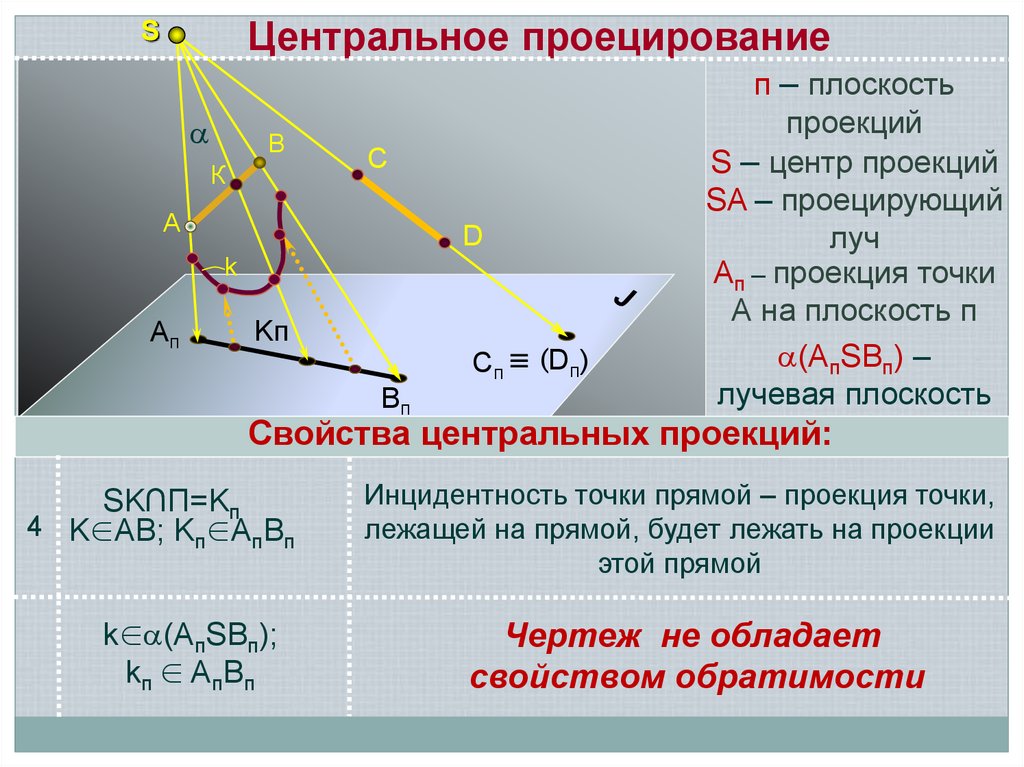
Центральное проецирование
S
В
К
C
А
D
k
Aп
Kп
Cп ≡ (Dп)
Bп
п – плоскость
проекций
S – центр проекций
SA – проецирующий
луч
Aп – проекция точки
А на плоскость п
(AпSBп) –
лучевая плоскость
Свойства центральных проекций:
SK∩П=Kп
4 K∈AB; Kп∈AпBп
k∈ (AпSBп);
kп ∈ AпBп
Инцидентность точки прямой – проекция точки,
лежащей на прямой, будет лежать на проекции
этой прямой
Чертеж не обладает
свойством обратимости

7.

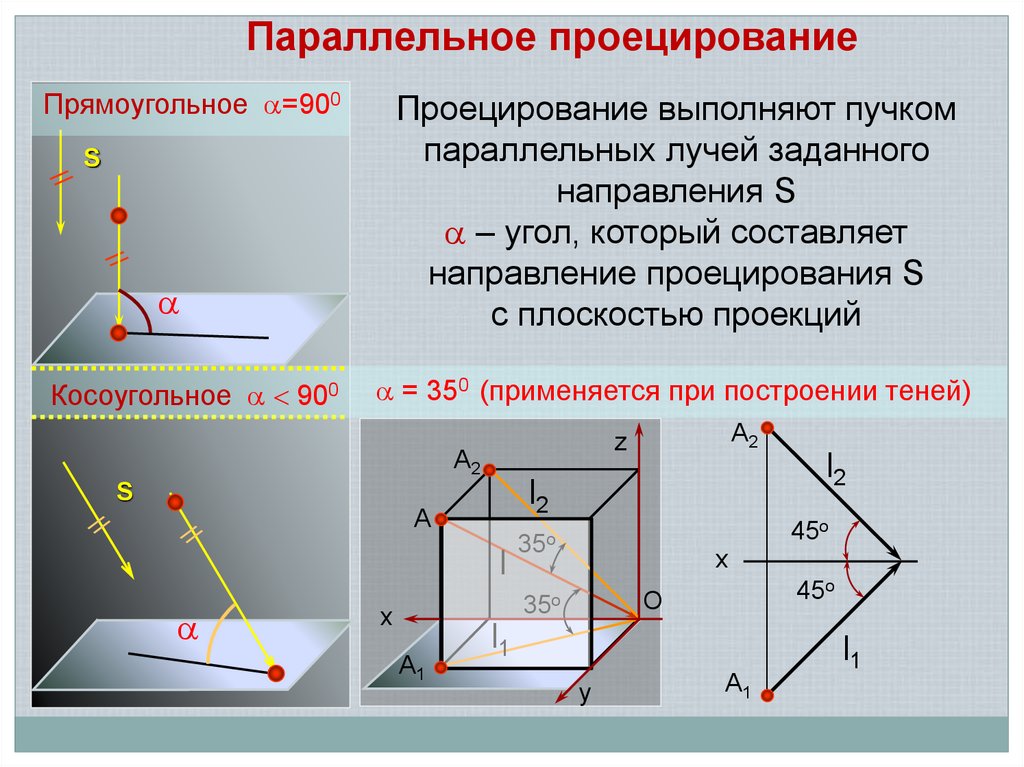
Параллельное проецирование
Прямоугольное =900
Проецирование выполняют пучком
параллельных лучей заданного
направления S
– угол, который составляет
направление проецирования S
с плоскостью проекций
S
Косоугольное 900
= 350 (применяется при построении теней)
A2
A
l
45о
35о
x
45о
О
35о
A1
l2
l2
S
x
A2
z
l1
l1
y
A1

8.

S
F
E
С
//
Cп
D
A
// N B
Dп
Eп
П
Aп
Nп
Bп
Fп
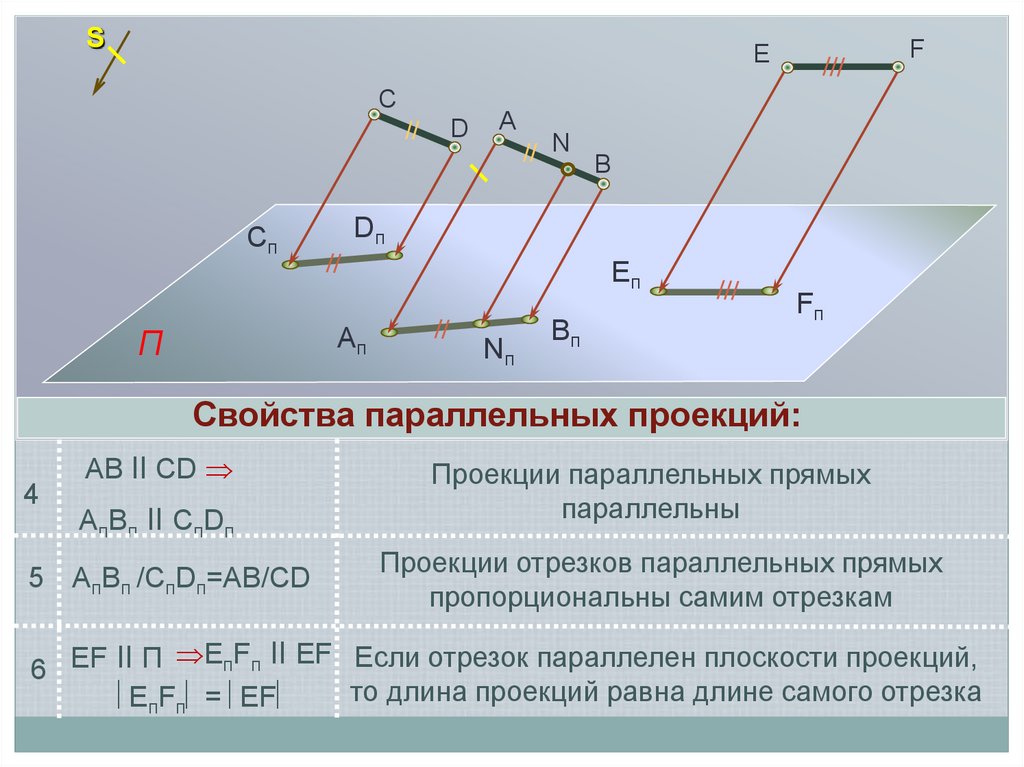
Свойства параллельных проекций:
4
AB ll CD
AпBп ll CпDп
5 AпBп /CпDп=AB/CD
Проекции параллельных прямых
параллельны
Проекции отрезков параллельных прямых
пропорциональны самим отрезкам
EпFп ll EF Если отрезок параллелен плоскости проекций,
6 EF ll П
то длина проекций равна длине самого отрезка
EпFп = EF

9.

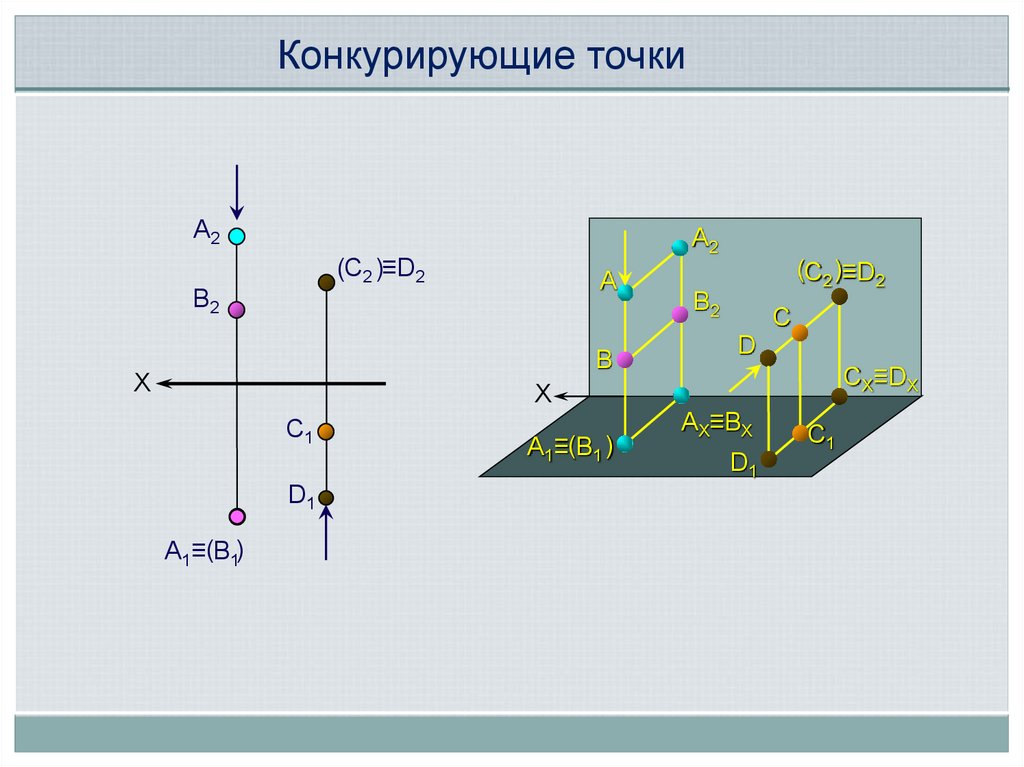
Конкурирующие точки
А2
А2
(C2 )≡D2
В2
А
В
X
X
С1
D1
А1≡(В1)
А1≡(В1 )
(C2 )≡D2
В2
С
D
CХ≡DХ
АХ≡ВХ
D1
С1

10.

ОБРАЗОВАНИЕ
КОМПЛЕКСНОГО ЧЕРТЕЖА

11.

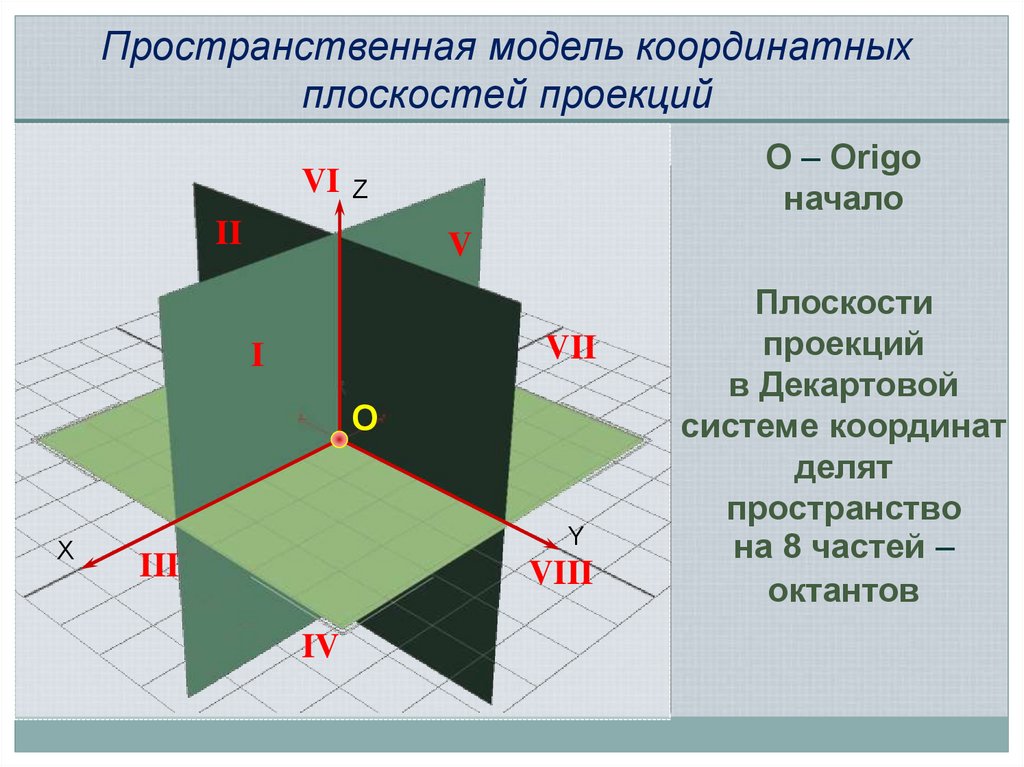
Пространственная модель координатных
плоскостей проекций
O – Origo
начало
VI Z
II
V
VII
I
O
X
Y
III
VIII
IV
Плоскости
проекций
в Декартовой
системе координат
делят
пространство
на 8 частей –
октантов

12.

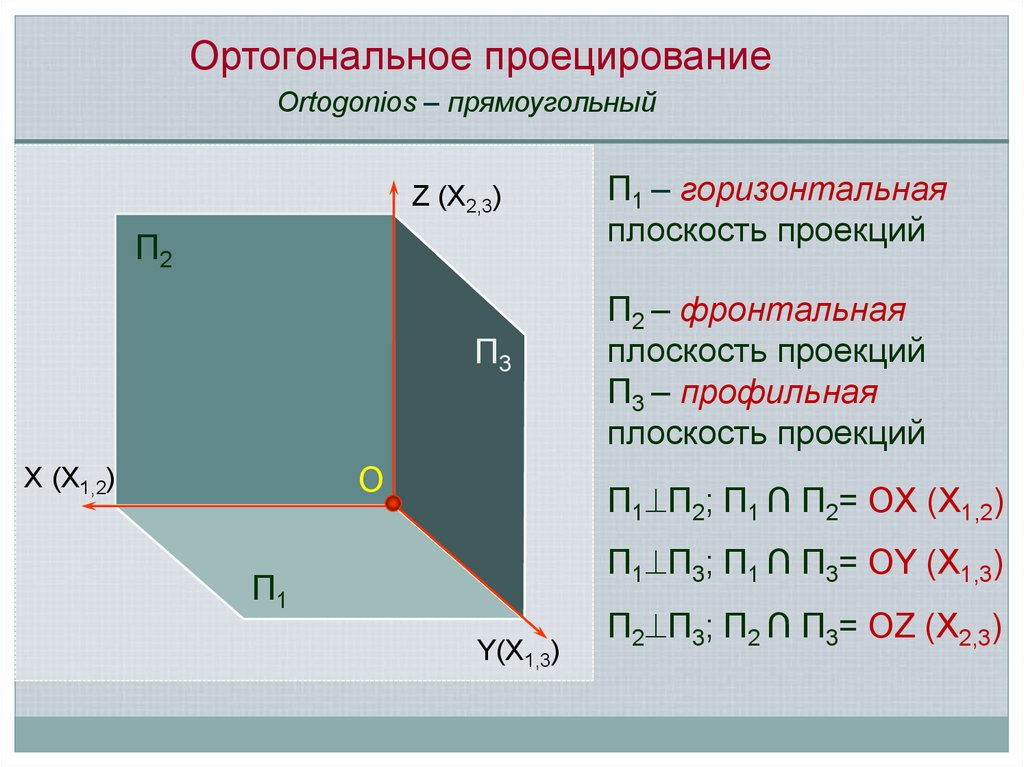
Ортогональное проецирование
Ortogonios – прямоугольный
Z (Х2,3)
П2
П3
О
Х (Х1,2)
П1 – горизонтальная
плоскость проекций
П2 – фронтальная
плоскость проекций
П3 – профильная
плоскость проекций
П1 П2; П1 ∩ П2= OX (X1,2)
П1 П3; П1 ∩ П3= OY (X1,3)
П1
Y(Х1,3)
П2 П3; П2 ∩ П3= OZ (X2,3)

13.

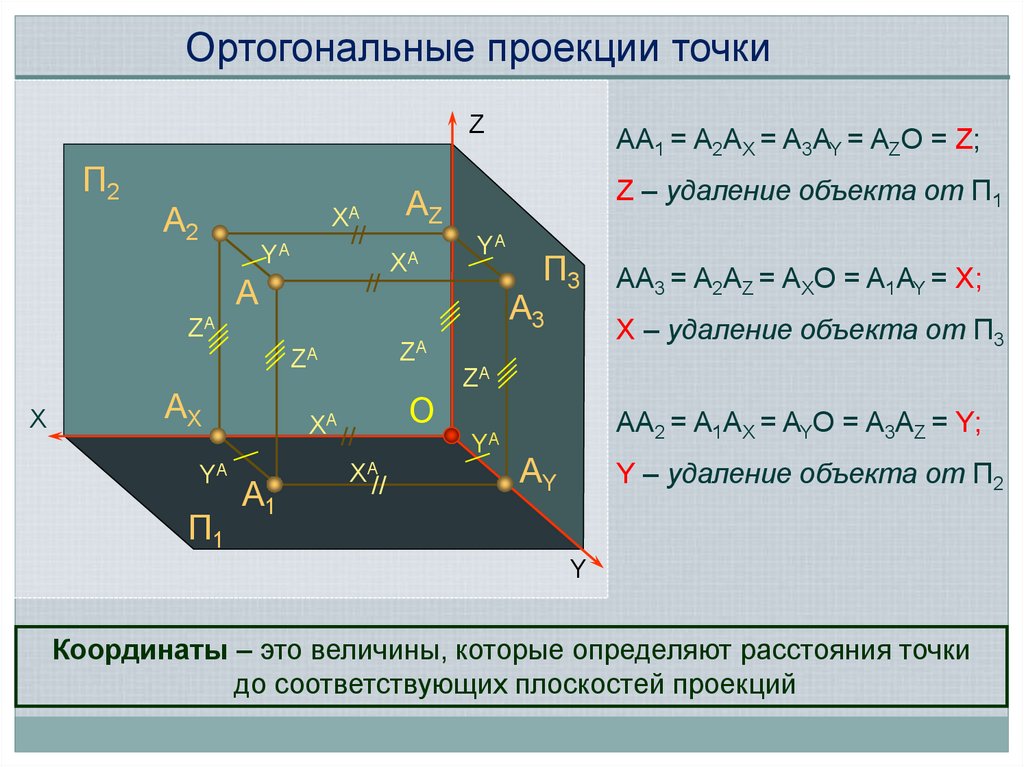
Ортогональные проекции точки
Z
П2
А2
//
А
//
ZА
АX
YА
П1
XА //
А1
XА
XА//
YА
П3
А3
ZА
ZА
X
Z – удаление объекта от П1
АZ
XА
YА
AA1 = A2AX = A3AY = AZO = Z;
AA3 = A2AZ = AXO = A1AY = X;
X – удаление объекта от П3
ZА
O
YА
AA2 = A1AX = AYO = A3AZ = Y;
АY
Y – удаление объекта от П2
Y
Координаты – это величины, которые определяют расстояния точки
до соответствующих плоскостей проекций

14.

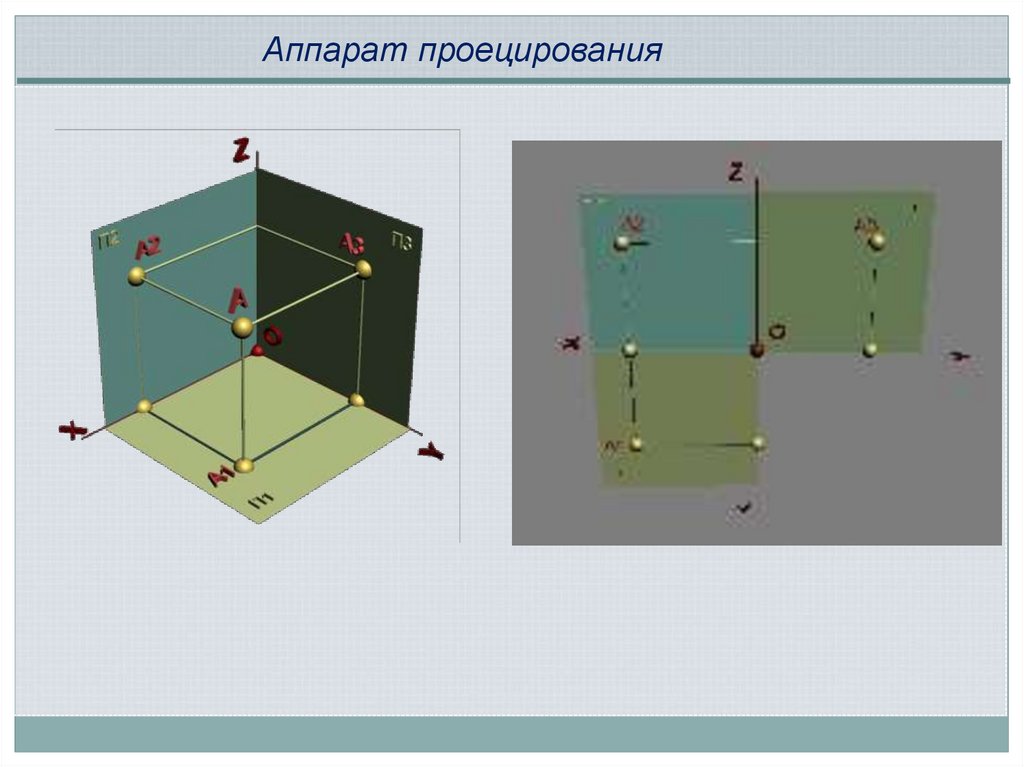
Аппарат проецирования

15.

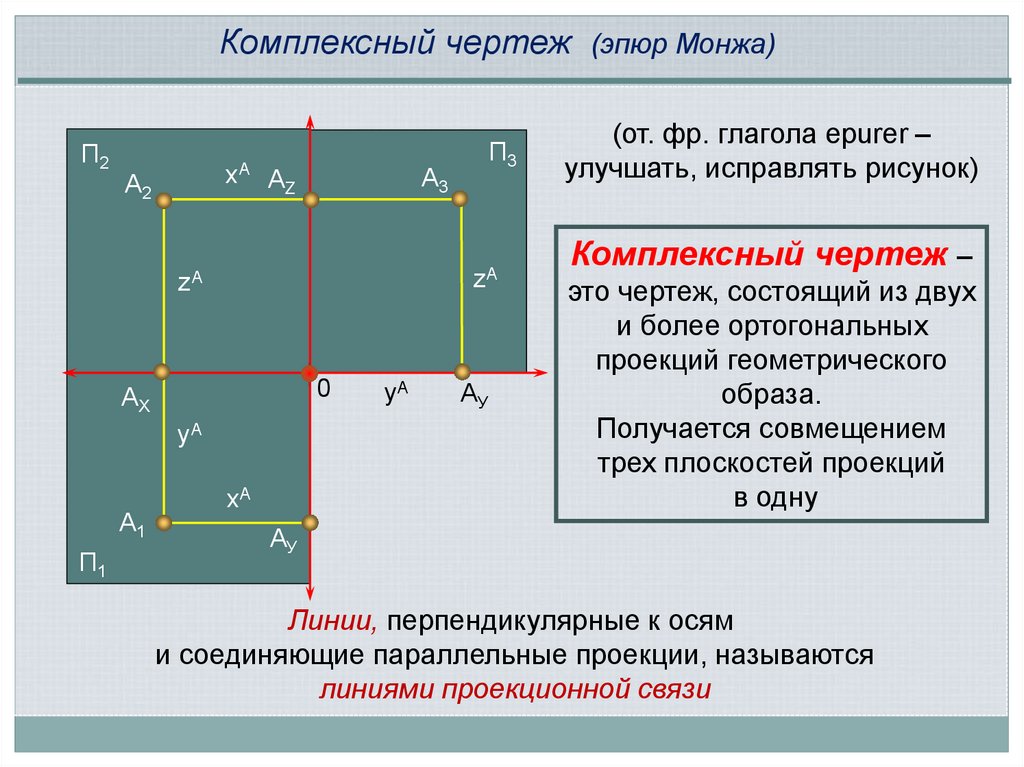
Комплексный чертеж (эпюр Монжа)
П2
xA АZ
А2
А3
zA
zA
0
АХ
yA
А1
П1
П3
xA
yA
АУ
(от. фр. глагола еpurer –
улучшать, исправлять рисунок)
Комплексный чертеж –
это чертеж, состоящий из двух
и более ортогональных
проекций геометрического
образа.
Получается совмещением
трех плоскостей проекций
в одну
АУ
Линии, перпендикулярные к осям
и соединяющие параллельные проекции, называются
линиями проекционной связи