Начертательная геометрия. Введение

1.

2.

ВВЕДЕНИЕ
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ - фундаментальная дисциплина,
составляющая основу инженерного образования
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ - раздел геометрии,
изучает методы изображения пространственных фигур
на чертеже и алгоритмы решения позиционных,
метрических и конструкционных задач
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ - база для создания чертежа
ЧЕРТЕЖ своеобразный язык, с помощью которого человек
имеет возможность изобразить на листе бумаги (плоскости)
пространственные геометрические фигуры
Начертательная геометрия… « является наивысшим средством для развития той таинственной и мало
поддающейся изучению точными науками способности человеческого духа, которая зовется
воображением и которая является ступенью к другой способности – фантазии, без которой не
совершаются великие открытия и изобретения»
Н. А. Рынин

3.

как сформировавшаяся наука
начертательная геометрия
(метод ортогонального проецирования)
возникла лишь в результате трудов
французского ученого и общественного
деятеля Гаспара Монжа,
который свел в стройную систему
весь разрозненный материал
по методу ортогонального проецирования,
и по заслугам считается его творцом
Гаспар Монж
(1746 1818)
он впервые предложил рассматривать
плоский чертеж из двух проекций
как результат совмещения двух плоскостей проекций
вращением вокруг их общей линии,
названной осью проекций

4.

ОБОЗНАЧЕНИЕ ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ
ТОЧКИ
обозначаются прописными буквами латинского алфавита или арабскими
цифрами:
A, B, C, D, …,L, M, N, …
1, 2, 3, 4, …, 12, 13, 14, …
ЛИНИИ
обозначаются строчными буквами латинского алфавита:
a, b, c, d, …,l, m, n, …
ПЛОСКОСТИ
обозначаются строчными буквами греческого алфавита:
α, β, γ, δ, …, ζ, η, λ, …
ПОВЕРХНОСТИ
обозначаются прописными буквами греческого алфавита:
Α, Β, Γ, Δ, …, Ζ, Η, Λ, …

5.

МЕТОДЫ ПРОЕЦИРОВАНИЯ
изображение объектов трехмерного пространства
на плоскости (в частности, построение чертежа)
получают методами проецирования
основа методов
проецирования -
процесс
образования тени

6.

1 метод – ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ
все лучи,
проецирующие предмет,
исходят из одной точки,
называемой
центром проекций
S – центр проекций
П – плоскость проекций
SA, SB – проецирующие лучи
AП – проекция точки А на плоскость П
BП – проекция точки B на плоскость П
S
А
B

7.

ОСНОВНЫЕ СВОЙСТВА
ЦЕНТРАЛЬНОГО ПРОЕЦИРОВАНИЯ
S
проекция точки –
есть точка
проекция прямой –
прямая,
кроме прямых,
совпадающих
с направлением
проецирующего луча
(проецирующих)
В
C
А
D
AП
BП
CП = (DП)
изображение проецирующей прямой вырождается в точку,
а фиксированные на ней точки являются
конкурирующими

8.

2 метод – ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ
все проецирующие лучи
проходят
параллельно
заданному направлению,
а значит и друг другу
S
А
B
S – направление проецирования
параллельное проецирование – частный случай центрального,
когда центр проецирования
расположен бесконечно далеко от плоскости проекций
и все проецирующие лучи становятся параллельными

9.

3 метод – ОРТОГОНАЛЬНОЕ (ПРЯМОУГОЛЬНОЕ)
ПРОЕЦИРОВАНИЕ
все проецирующие лучи
проходят
перпендикулярно
S
плоскости проекций
А
B
AП
BП
S – направление проецирования
S П
ортогональное проецирование – частный случай параллельного

10.

СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕЦИРОВАНИЯ
проекции
параллельных прямых параллельны
при параллельном
проецировании
сохраняются
пропорции

11.

СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕЦИРОВАНИЯ
плоская фигура
параллельная плоскости
проекций проецируется
в тождественную фигуру
точка пересечения
проекции
пересекающихся
линий есть проекция
пересечения этих
линий

12.

ОБРАЗОВАНИЕ
КОМПЛЕКСНОГО ЧЕРТЕЖА
И ЗАДАНИЕ
ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ
НА ЭТОМ ЧЕРТЕЖЕ

13.

КОМПЛЕКСНЫЙ ЧЕРТЕЖ (КЧ)
(эпюр Монжа)
суть метода Монжа
заключается
в проецировании
различных геометрических
единиц - точек, прямых,
фигур и поверхностей
на две или три
взаимно перпендикулярные
плоскости,
которые называются:
- горизонтальная (П1)
- фронтальная (П2)
- профильная (П3)

14.

КОМПЛЕКСНЫЙ ЧЕРТЕЖ
линии пересечения
плоскостей проекций
называют
осями проекций:
ОХ, ОY и ОZ
при проецировании точки А
на все три плоскости проекций
получается три ее проекции:
горизонтальная - А1
фронтальная - А2
профильная - А3
пространственное (наглядное)
изображение

15.

КОМПЛЕКСНЫЙ ЧЕРТЕЖ
для построения комплексного чертежа
пространственное (наглядное)
изображение нужно преобразовать
в плоскостное
при этом
плоскости проекций разворачиваются:
фронтальная плоскость (П2) остается на месте,
горизонтальная (П1) опускается вниз
до совмещения с фронтальной плоскостью,
а профильная (П3) разворачивается вправо
до совмещения с фронтальной
ось ОY раздваивается – она участвует в образовании
горизонтальной плоскости проекций (П1) и необходима
для формирования профильной плоскости проекций (П3)

16.

КОМПЛЕКСНЫЙ ЧЕРТЕЖ
расстояние от точки А
до П1 выражается координатой Z,
до П2 - координатой Y,
до П3 - координатой Х
координаты указывают
в миллиметрах, отсчет ведется
от начала координат - 0
все три проекции точки
взаимосвязаны между собой
линии,
соединяющие проекции
точки А, называются
линиями связи –
всегда перпендикулярны
осям проекций
А (х, y, z)

17.

КОМПЛЕКСНЫЙ ЧЕРТЕЖ
(эпюр Монжа)
П2
А3
А2
П3
0
наглядное изображение
А1
П1
комплексный чертеж –
чертеж, состоящий из двух или более
связанных между собой
ортогональных проекций геометрического
объекта
получается совмещением всех плоскостей
проекций в одну

18.

КОМПЛЕКСНЫЙ ЧЕРТЕЖ
плоскости проекций:
П2
z23
А2
П3
А3
x
П1 – горизонтальная
П2 – фронтальная
П3 – профильная
проекции точки А:
z
z
x12
y3
y
0
y
А1
П1
А (х, y, z)
А1 – горизонтальная
А2 – фронтальная
А3 – профильная
координаты точки:
х – широта
y – глубина
z – высота
линии проекционной связи –
x
y1
прямые линии, соединяющие
разноименные проекции точки
на комплексном чертеже

19.

КОМПЛЕКСНЫЙ ЧЕРТЕЖ ТОЧКИ
ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ
ТОЧКИ ПО ЕЕ КООРДИНАТАМ

20.

КОМПЛЕКСНЫЙ ЧЕРТЕЖ ТОЧКИ
П2
z23
А2
y
x
z
проекции точки А:
П3
А3
А1 – горизонтальная
А2 – фронтальная
А3 – профильная
z
А (х, y, z)
y3
x12
0
y
А1
П1
координаты точки:
х – широта
y – глубина
z – высота
комплексный чертеж точки –
x
y1
чертеж, состоящий из двух или более
связанных между собой
ортогональных проекций точки

21.

КОМПЛЕКСНЫЙ ЧЕРТЕЖ ТОЧКИ
точка считается заданной,
если имеются все три ее координаты – х, y, z
либо точка задается записью
А (х, y, z)
либо точка задается на комплексном чертеже одним из трех вариантов
П2
А2
x
z23
П3
П2
z
А2
x
z23
y
z
x12
П3
А3
z
y3
П1
y3
0
y
x
y1
П1
П3
А3
x12
0
y
А1
y
z
x12
0
z23
П2
А1
y1
П1
x
y1
либо точка задается на комплексном чертеже одной проекцией и недостающей
координатой отдельно в виде записи
координаты точки:
х – широта y – глубина z – высота
y3

22.

ПОЛОЖЕНИЕ ТОЧКИ
Х 0
Y 0
Z 0
точка – в пространстве
одна
координата = 0
точка – принадлежит
плоскости проекций
две
координаты = 0
точка – принадлежит
оси координат
три
координаты = 0
точка – принадлежит
началу координат

23.

ПОЛОЖЕНИЕ ТОЧКИ
принадлежность точки плоскости проекций
Х=0
Y 0
Z 0
точка П3
Х 0
Y=0
Z 0
точка П2
Х 0
Y 0
Z=0
точка П1

24.

ПОЛОЖЕНИЕ ТОЧКИ
принадлежность точки оси координат
Х 0
Y=0
Z=0
точка OX12
Х=0
Y 0
Z=0
точка OY13
Х=0
Y=0
Z 0
точка OZ23

25.

КОНКУРИРУЮЩИЕ ТОЧКИ

26.

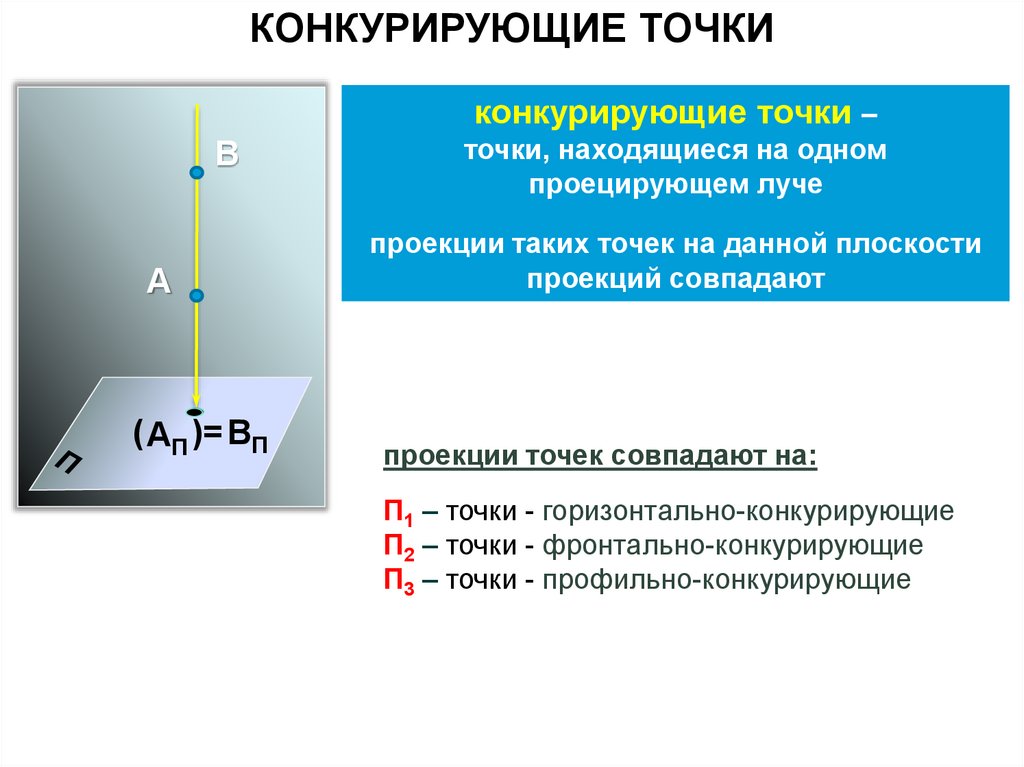
КОНКУРИРУЮЩИЕ ТОЧКИ
конкурирующие точки –
B
А
( AП )= BП
точки, находящиеся на одном
проецирующем луче
проекции таких точек на данной плоскости
проекций совпадают
проекции точек совпадают на:
П1 – точки - горизонтально-конкурирующие
П2 – точки - фронтально-конкурирующие
П3 – точки - профильно-конкурирующие

27.

КОНКУРИРУЮЩИЕ ТОЧКИ
B
А
( AП )= BП
по конкурирующим точкам
определяют
видимость на чертеже:
у горизонтально-конкурирующих
видимая та,
у которой больше z – высота
у фронтально-конкурирующих
видимая та,
у которой больше y – глубина
у профильно-конкурирующих
видимая та,
у которой больше х – широта
все невидимые точки
(которые расположены за видимой точкой)
на комплексном чертеже заключаются в скобки (Ап)

28.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

29.

Задача 1
Построить по координатам проекции точки К(20;30;15)
Z23
К2
X12
15
20
30
20
20
К3
10
Y3
10
О 10
10
30
20
К1
30
Y1
см. решение – щелчок мыши
30
20
30

30.

Задача 2
1.
2.
По двум проекциям построить третью, профильную проекцию точки М
Записать координаты точки
Z23
М2
30
20
М3
40
10
X12
20
Y3
10
О 10
20
30
40
10
40
20
30
М1
40
Y1
см. решение – щелчок мыши
М(25; 40; 20)

31.

Задача 3
Z23
С2
AиB–
С3
40
( А2) =В2
А3
30
В3
фронтальноконкурирующие
точки
CиD–
20
D2
X12
D3
10
40
30
20
10
О
А1
10
20
30
40
Y3
10
30
1.Построить по координатам проекции
точек А,В,С,D:
А(25;10;30), В(25;40;30)
С(40;25;45), D(40;25;10)
40
2. Какие точки являются
конкурирующими?
20
С1 =(D1 )
В1
см. решение – щелчок мыши
горизонтальноконкурирующие
точки
Y1

32.

Задача 4
Какой плоскости проекций принадлежит точка А?
z
Z23
А2
xА
П2
А3
А=А2
А3
П3
zА
X12
zА
Y3
xА
А1
А1
X
O
O
П1
y
Y1
YА=0
А П2
см. решение – щелчок мыши

33.

Задача 5
Какой плоскости проекций принадлежит точка В?
z
Z23
П2
В3
В2
yB
xB
X12
yB
yB
В1
П3
Y3
O
B=В2
O
X
П1
xB
В3
В1
Y1
y
Z=0
B П1
см. решение – щелчок мыши

34.

Задача 6
Какой плоскости проекций принадлежит точка С?
Z23
С2
yC
zC
X12
O
z
С3
П2
C2
zC
yC
C3=C
Y3
X
yC
П1
С1
П3
O
C1
y
Y1
Х=0
С∈П3
см. решение – щелчок мыши