Similar presentations:
Приложения криволинейных интегралов в геометрии и механике
1. Приложения криволинейных интегралов в геометрии и механике
2.
1) Длина кривой.Если подынтегральная функция
f(x, y, z) ≡ 1, то из определения
КРИ-1 следует, что он равен
длине кривой, по которой
ведется интегрирование:
l ds.
l
3.
2) Масса кривой.Если подынтегральная функция
γ (x, y, z) определяет плотность
в каждой точке кривой, то массу
кривой можно найти по формуле
M ( x, y, z )ds.
l
4.
• 3) Моменты кривой l:статические моменты плоской
кривой l относительно осей Ох и
Оу:
M x y ( x, y)ds, M y x ( x, y, z )ds
l
l
5.
момент инерциипространственной кривой
относительно начала координат:
I 0 ( x y z )ds
2
2
2
l
моменты инерции кривой
относительно координатных
осей:
I x ( y 2 z 2 )ds, I y ( x 2 z 2 )ds, I z ( x 2 y 2 )ds
l
l
l
6.
4) Координаты центра масскривой вычисляются по
формулам
xc
zc
x
(
x
,
y
,
z
)
ds
l
M
z
(
x
,
y
,
z
)
ds
l
M
, yc
y
(
x
,
y
,
z
)
ds
l
M
,
7.
F {P, Q, R} ,• 5) Работа силы
действующей на точку,
движущуюся по кривой (АВ):
Pdx
Qdy
Rdz
F
d
r
( AB )
( AB )
8.
Пример. Найти массу кривойс
линейной плотностью ,
2
заданной в полярных
координатах уравнением ρ = 4φ,
где
3
3
.
9.
• Решение.2
M ( ), d
2
2
1
2
3
4
3
4
4 2 1d
2
3
8 2
1d( 1) 1
3
2
2
3
2
2
3 3
2
3
3
3
8
2
2
2
2
4 9 9 .
81
10.
• Пример. Вычислить работу2 3
2 3
векторного поля F x y , y z , xyz
вдоль отрезка прямой от точки
А(-2;-3;1) до точки В(1;4;2).
11.
• Решение. Найдем каноническиеи параметрические уравнения
прямой АВ:
12.
y y1x x1
z z1
x 2 y 3 z 1
t
t,
x2 x1 y 2 y1 z2 z1
3
7
1
x 3t 2, dx 3dt ;
y 7t 3, dy 7 dt ;
z t 1, dz dt.
A
Fx dx Fy dy Fz dz
( AB )
1
t( A) 0,
t( B) 1
x 2 y 3dx y 2 z 3dy xyzdz
( AB )
3 3t 2 7t 3 7 7 t 3 t 1 3t 2 7 t 3 t 1 dt
2
3
2
3
0
1
5
4
3
2
9604
t
6056
t
25305
t
8177
t
993t 261 dt
0
1
9604t
6056t
25305t
8177 t
993t
261t 4225, 55.
5
4
3
2
6
0
6
5
4
3
2
13.
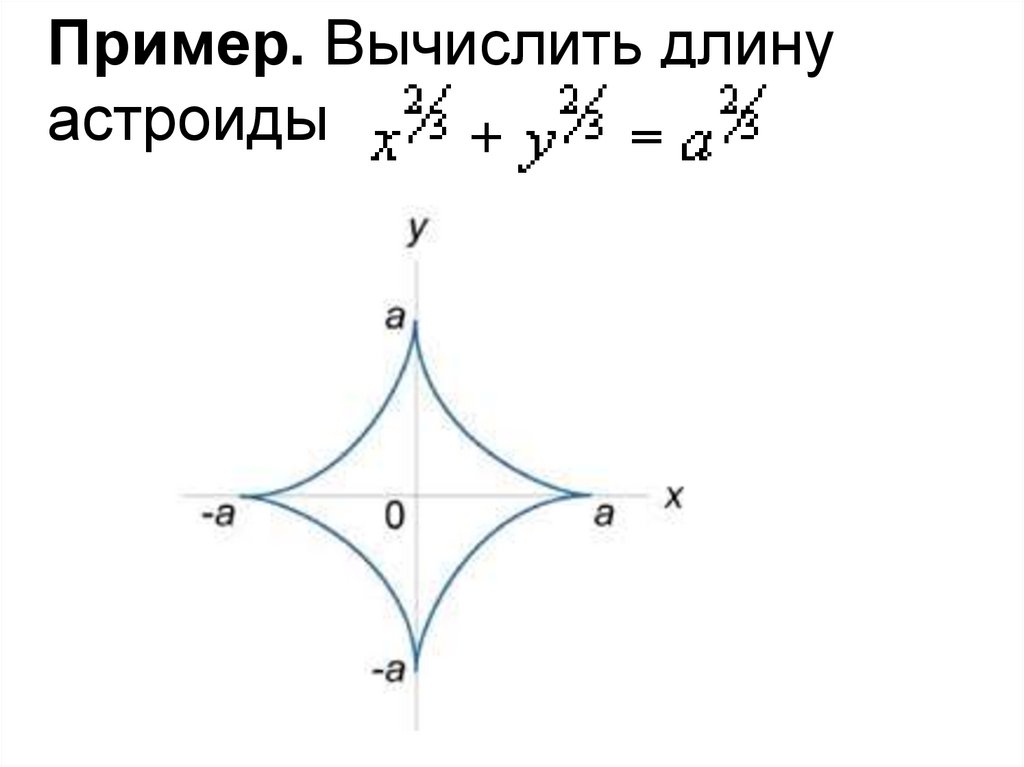
Пример. Вычислить длинуастроиды
14.
• Решение. В силу симметрии,достаточно вычислить длину
кривой, лежащей в первом
квадранте, и затем умножить
результат на 4. Уравнение
астроиды в первом квадранте
имеет вид
15.
16.
Пример. Найти длину астроидыx=a
3
cos t,
y=a
3
sin t
17.
• Решение. Воспользуемсяформулой
В нашем случае
18.
19.
Поскольку кривая симметричнаотносительно осей координат, то
20.
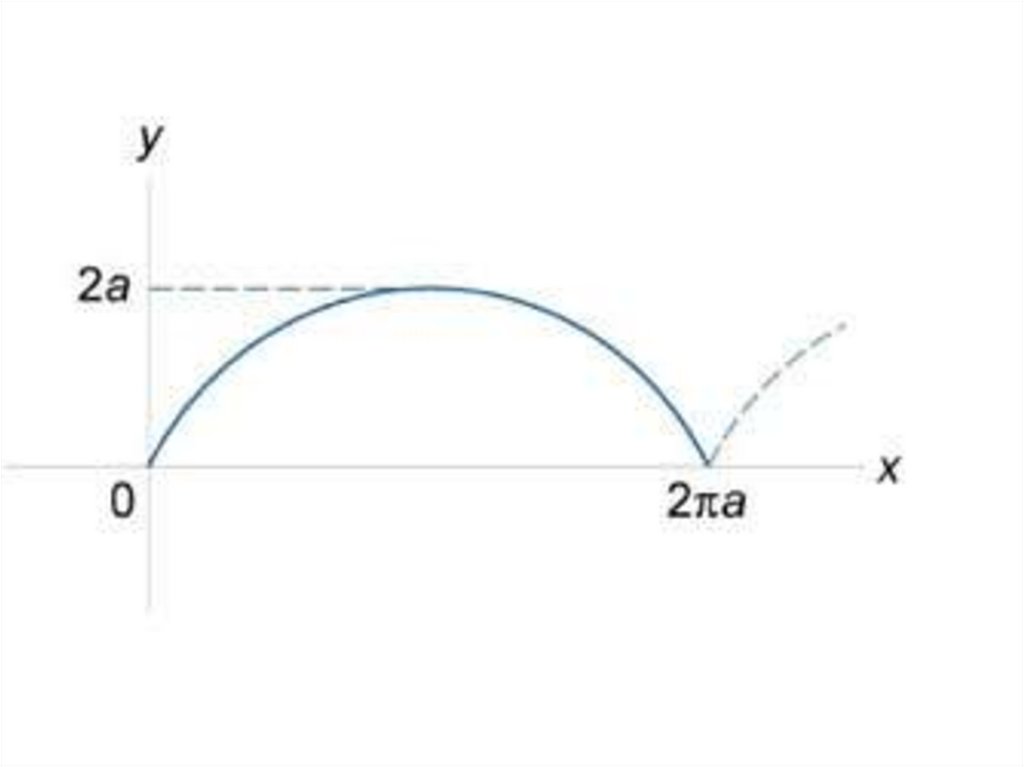
• Пример. Найти длину циклоиды,заданной в параметрическом
виде вектором
в интервале
21.
22.
Решение. Воспользуемсяформулой
23.
• Производные:24.
25.
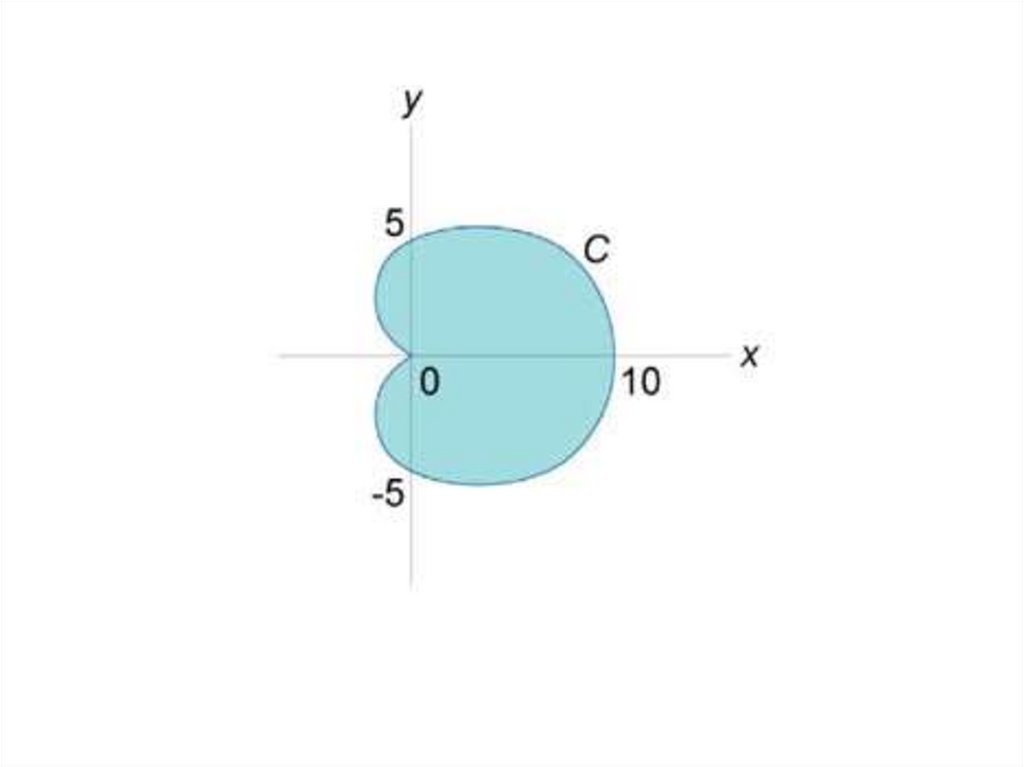
• Пример. Найти длинукардиоиды, заданной в
полярных координатах
уравнением r 5(1 cos )
26.
27.
• Решение. Используемсоотношение
В силу симметрии кардиоиды
достаточно найти половину ее
длины, а затем удвоить
полученный результат.
28.
drr
(5(1 cos )) 5 sin
d
Длина кардиоиды выражается в
виде
29.
L (5(1 cos )) ( 5 sin ) d2
2
0
5 1 2 cos cos sin d
2
2
0
0
0
5 2 2 cos d 5 2(1 cos ) d
30.
5 2 2 cos0
2
2
d 10 cos
0
2
2
d
Так как cos 2 0 при 0 , то
cos
2
2
cos
2
cos
2
Окончательно находим длину:
31.
L 10 cos0
2
d 10 cos d
2
2
0
20 cos d 20 sin
2
2
2
0
0
20 sin sin 0 20(1 0) 20
2
32.
• Длина всей кардиоиды равна2L 2 20 40
33.
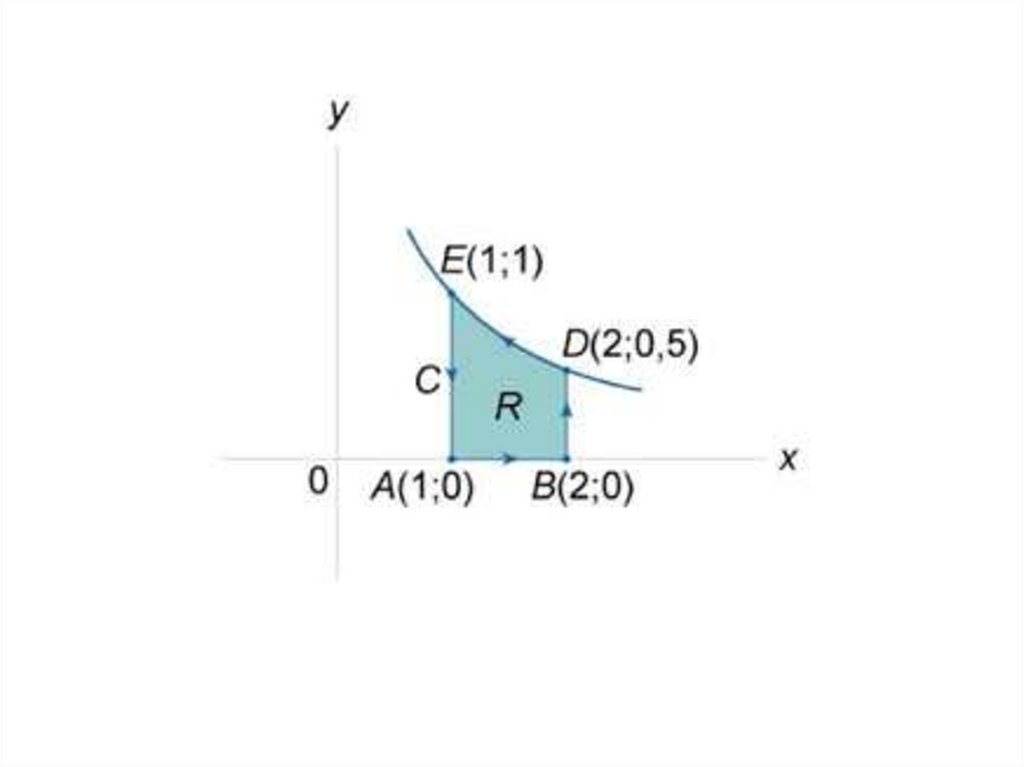
• Пример. Найти площадьобласти, ограниченной
гиперболой
, осью Ox и
вертикальными прямыми
x = 1, x = 2.
34.
35.
• Решение. Вычислим площадь спомощью криволинейного
интеграла.
Найдем отдельно каждый из
интегралов.
36.
37.
• Следовательно, площадьзаданной области равна
38.
• Пример. Найти статическиемоменты дуги однородной
астроиды
относительно осей координат.
39.
• Решение. Дуга астроидыоднородна, следовательно,
плотность в каждой точке
постоянна. Пусть
. Запишем
уравнение астроиды в
параметрическом виде
• где
40.
41.
• По условиюследовательно,
dl = 3a sin t cos t dt
42.
43.
44.
45.
46.
47.
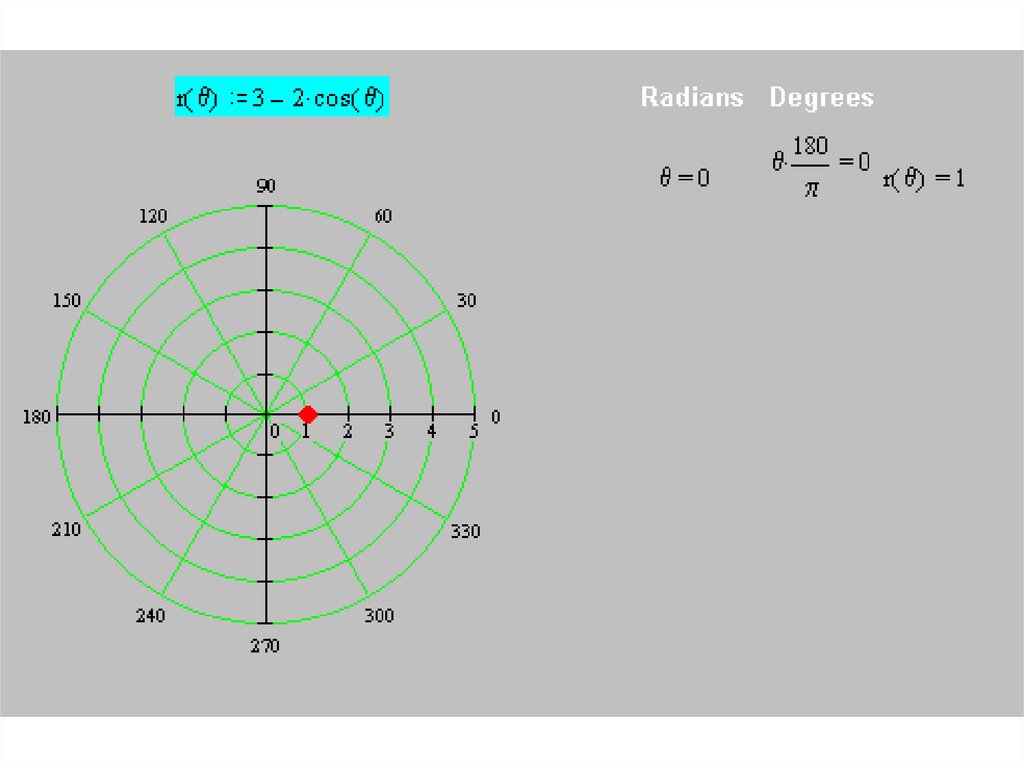
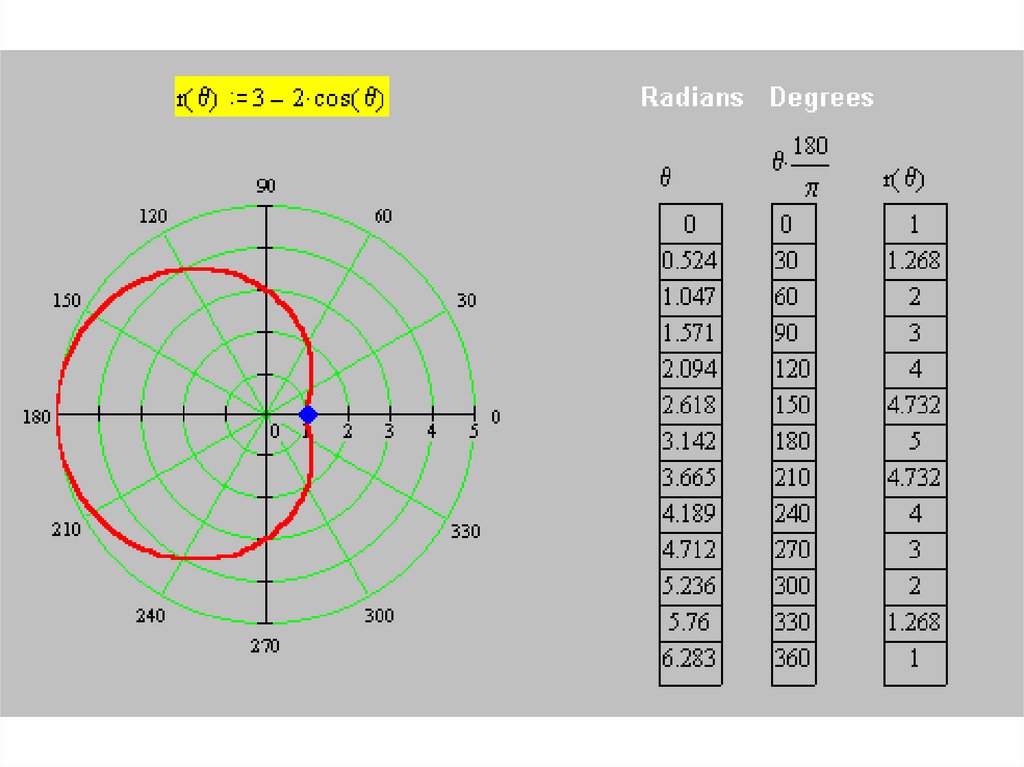
• Построим кривуюr(θ) = 3 – 2 cos θ
48.
49.
50.
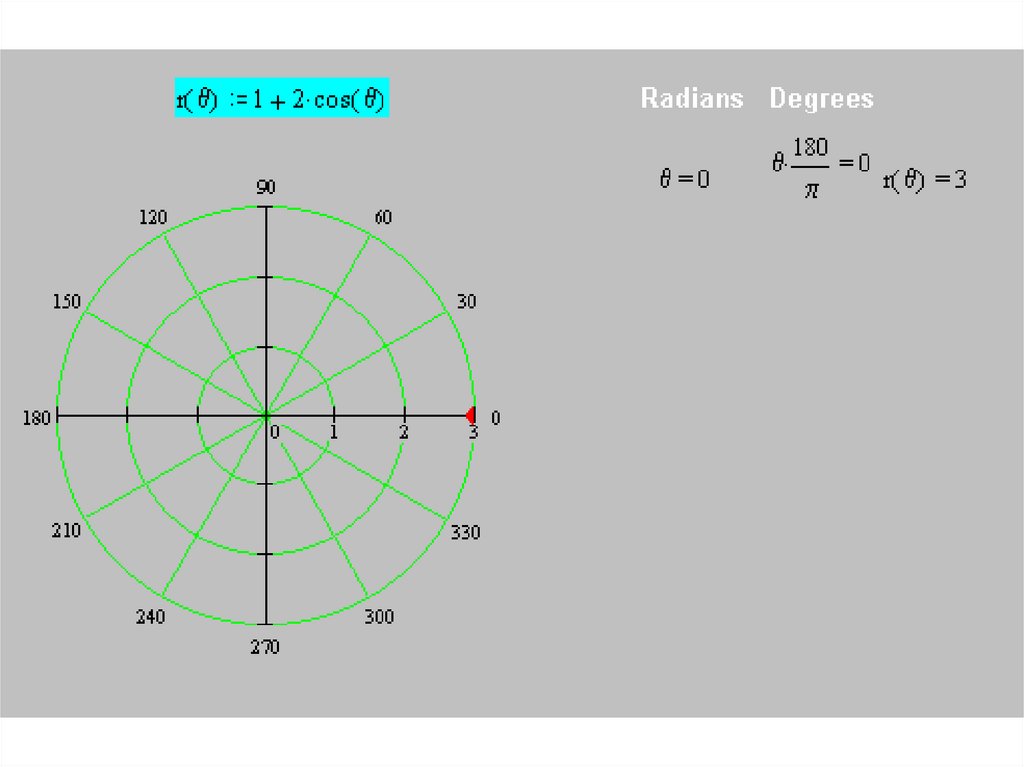
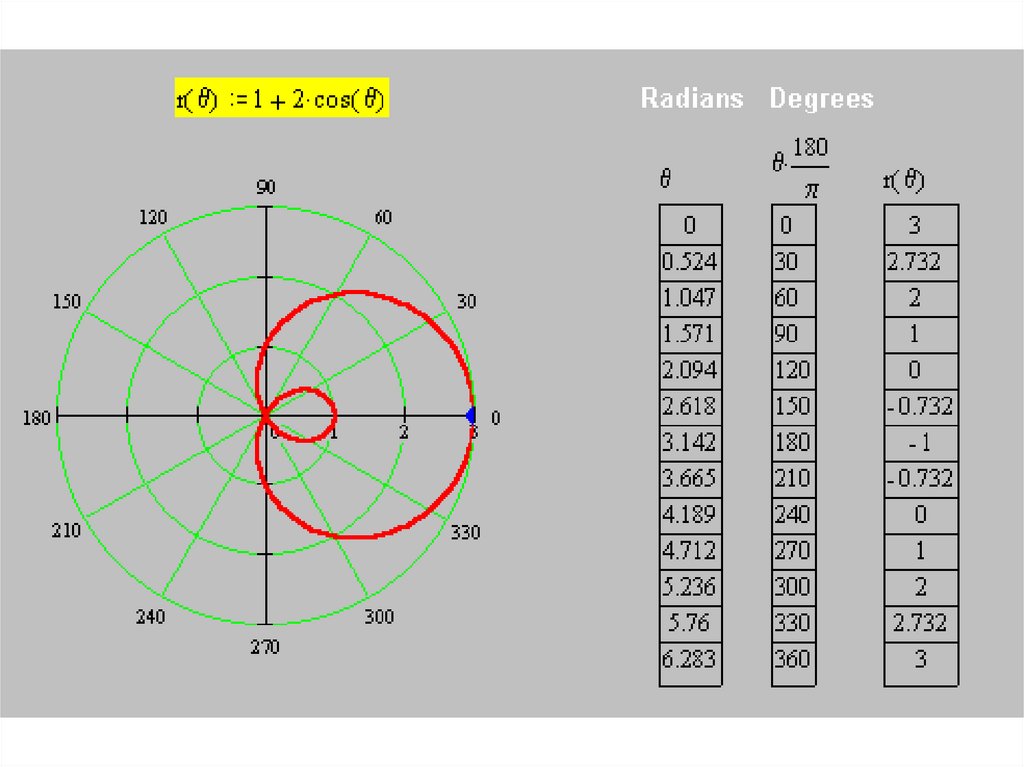
• Построим кривуюr(θ) = 1+ 2 cos θ
51.
52.
53.
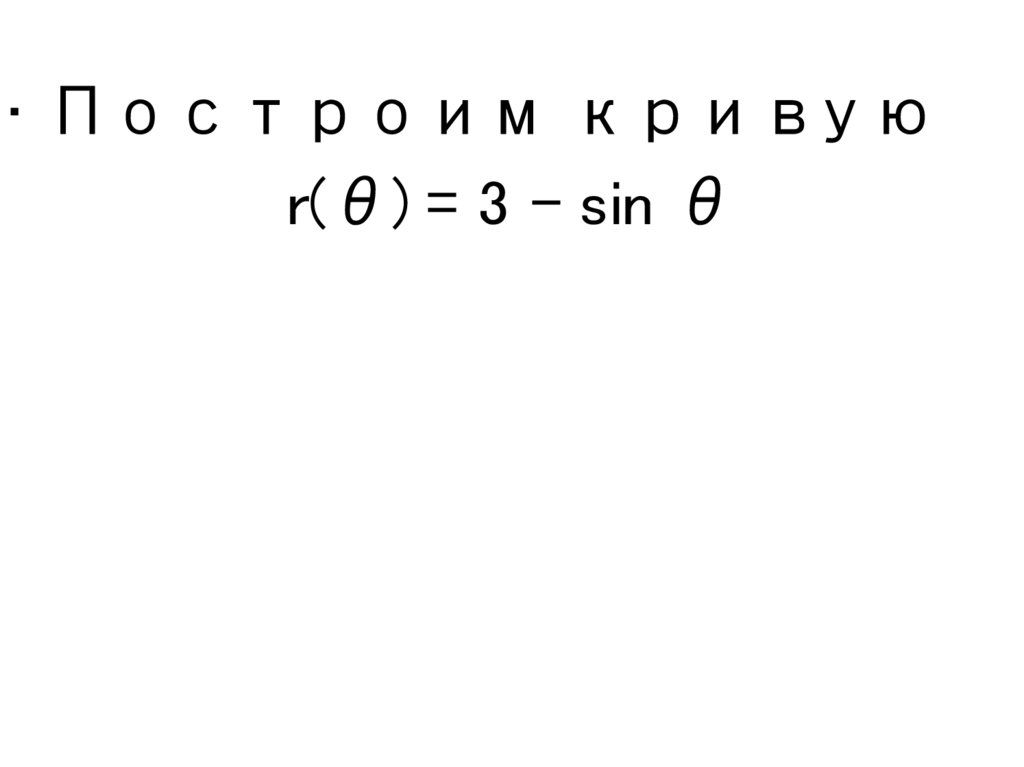
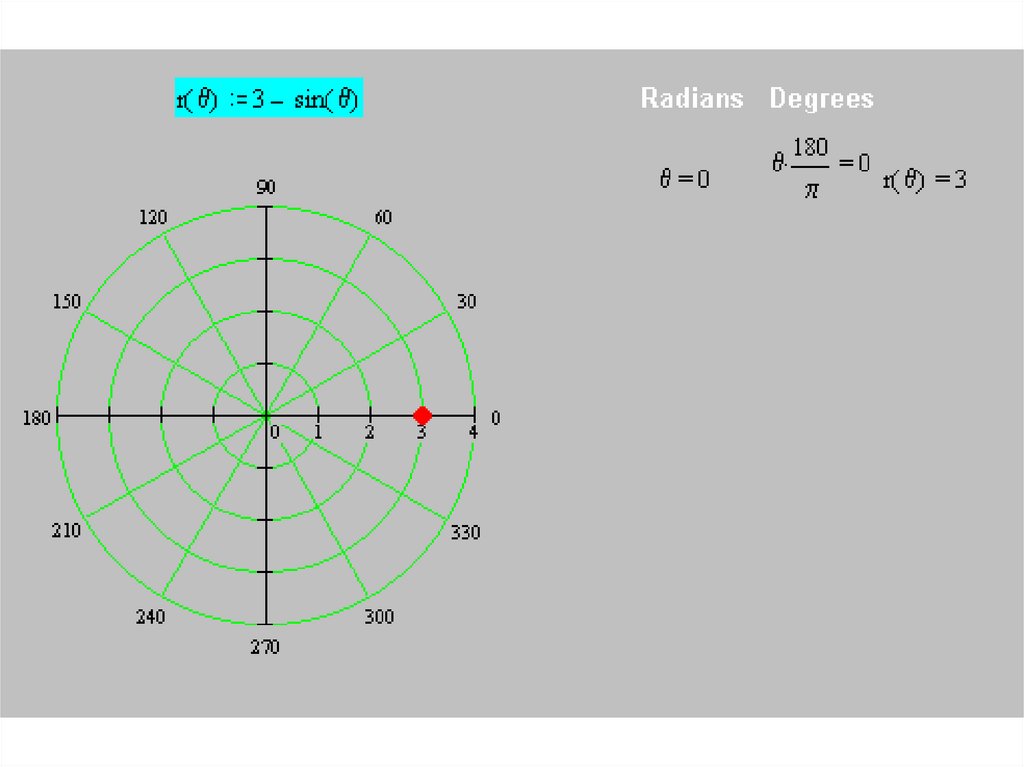
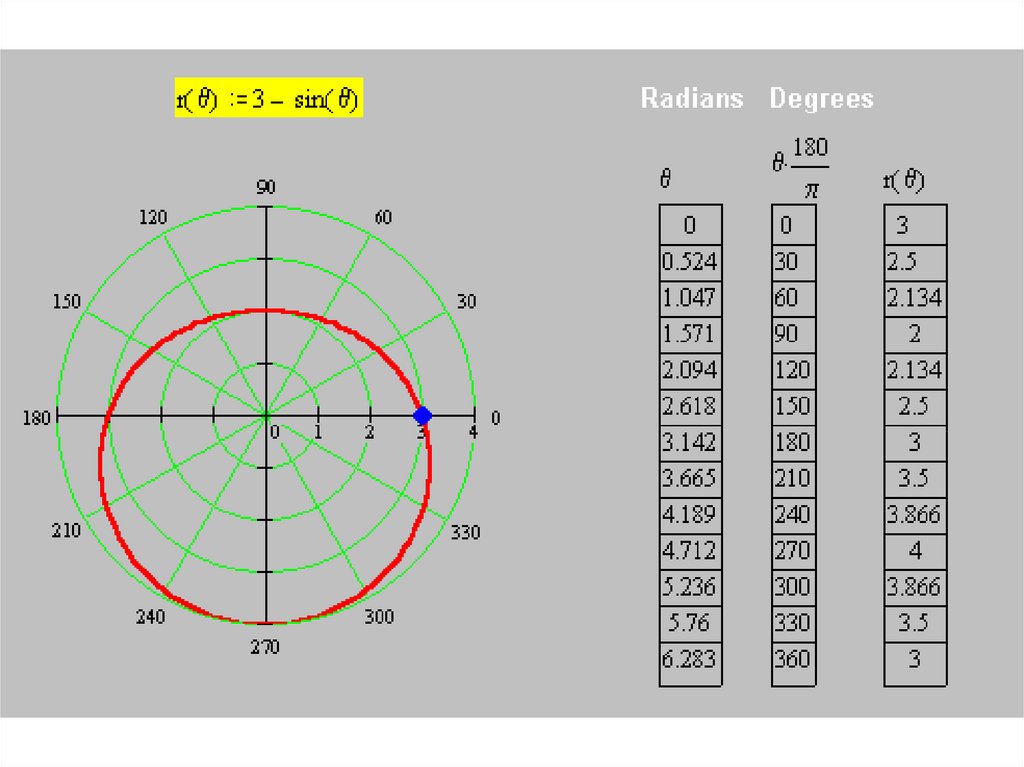
• Построим кривуюr(θ) = 3 – sin θ
54.
55.
56.
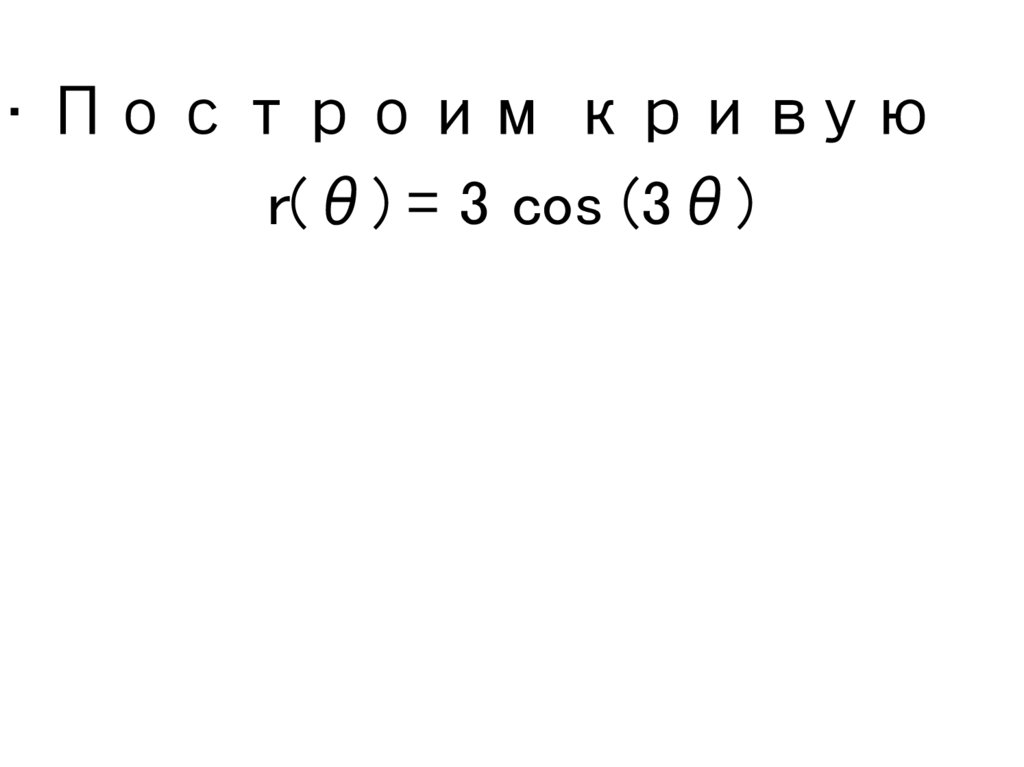
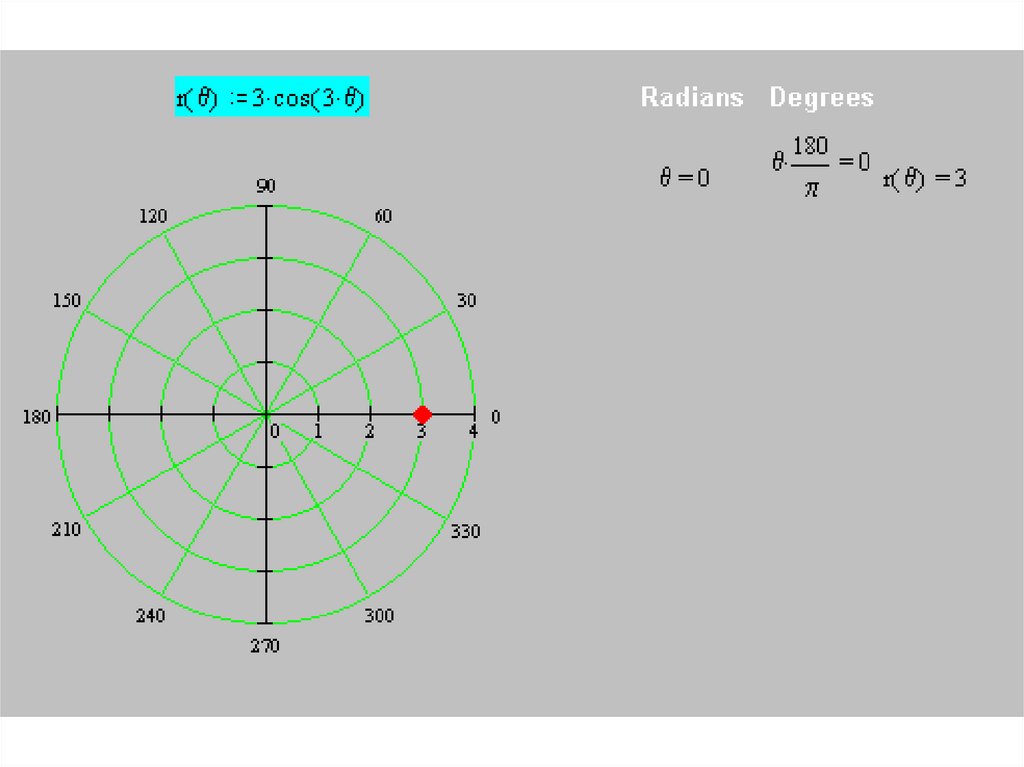
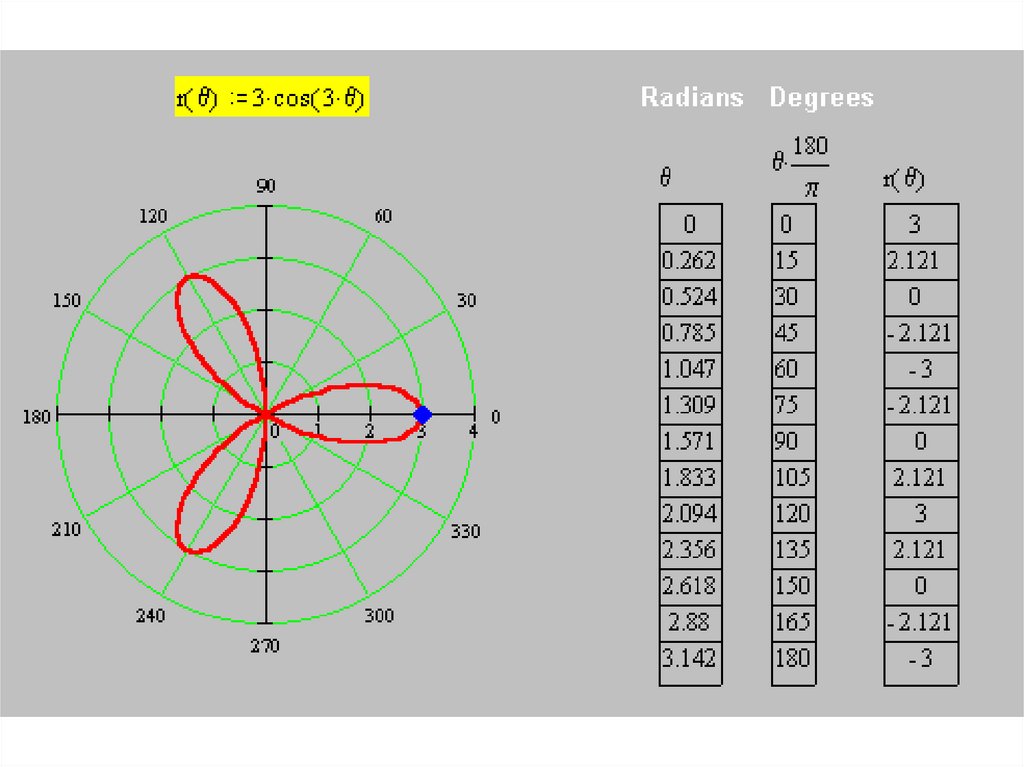
• Построим кривуюr(θ) = 3 cos (3θ)
57.
58.
59.
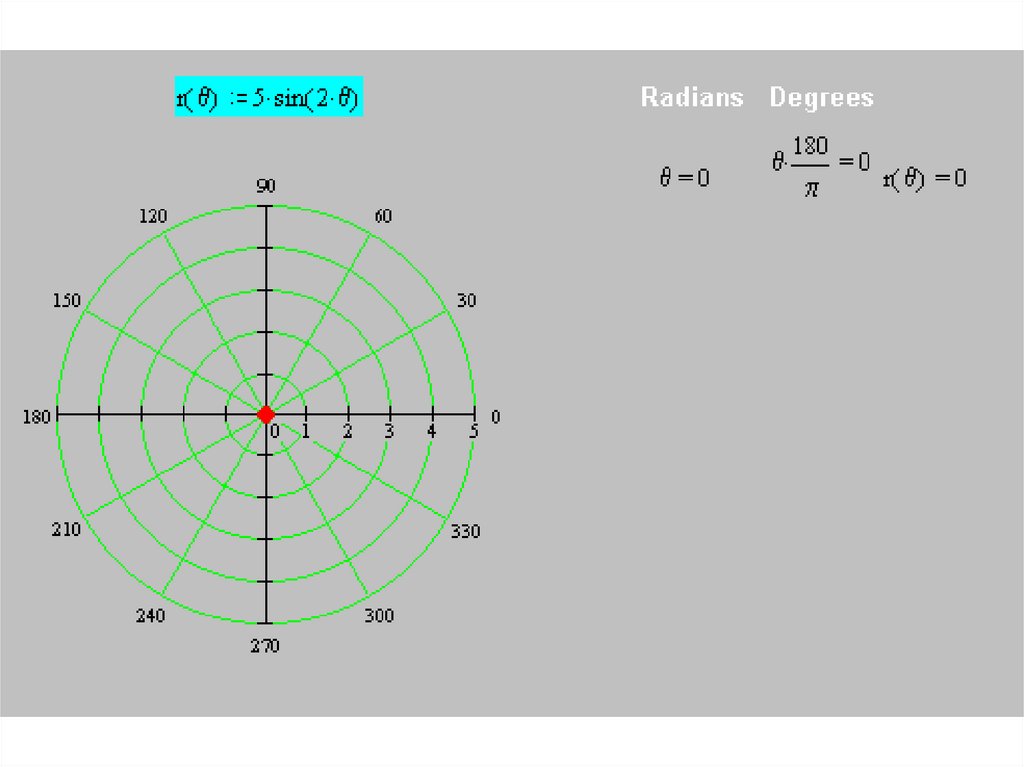
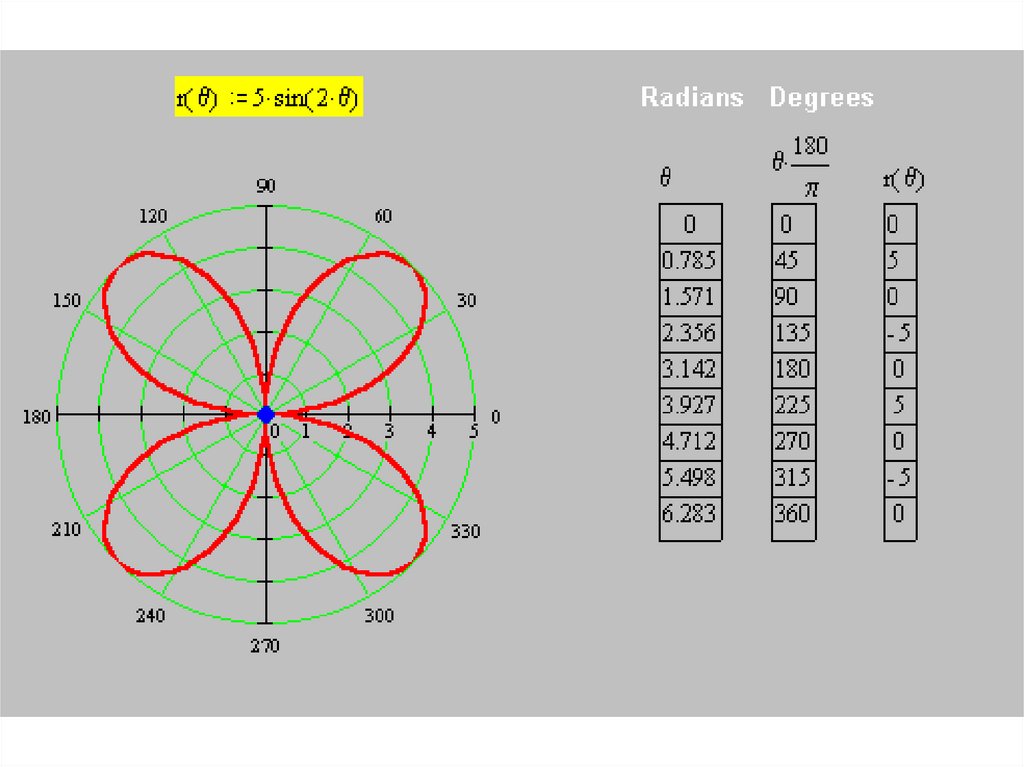
• Построим кривуюr(θ) = 5 sin (2θ)
60.
61.
62.
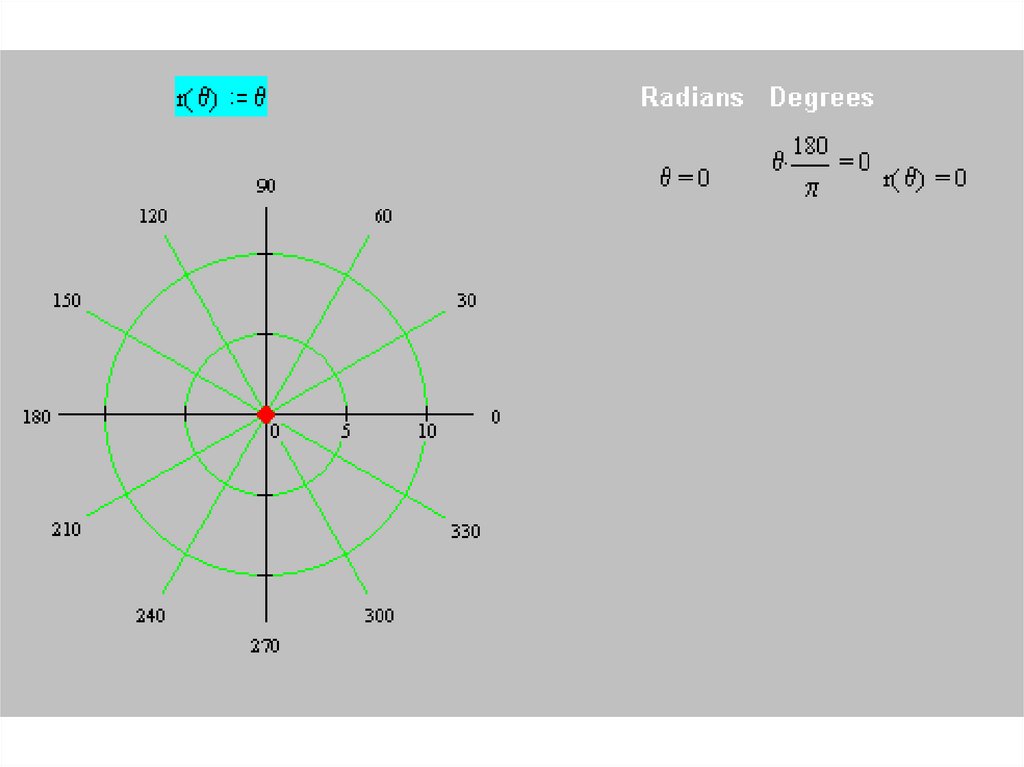
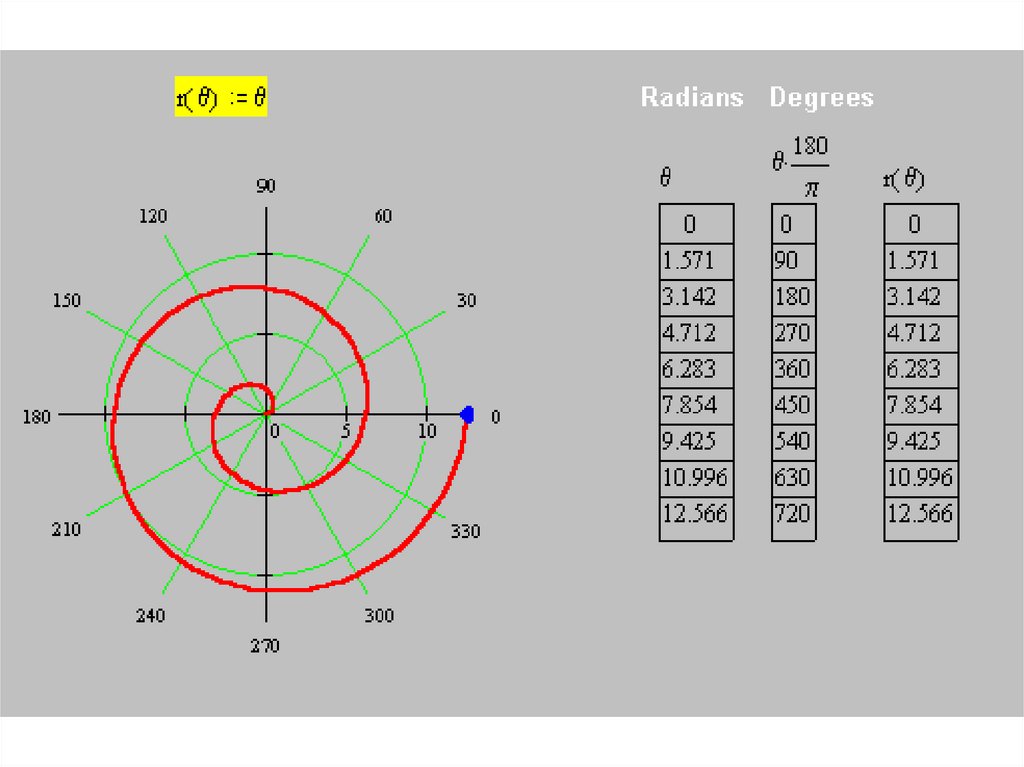
• Построим кривуюr(θ) = θ
63.
64.
65.
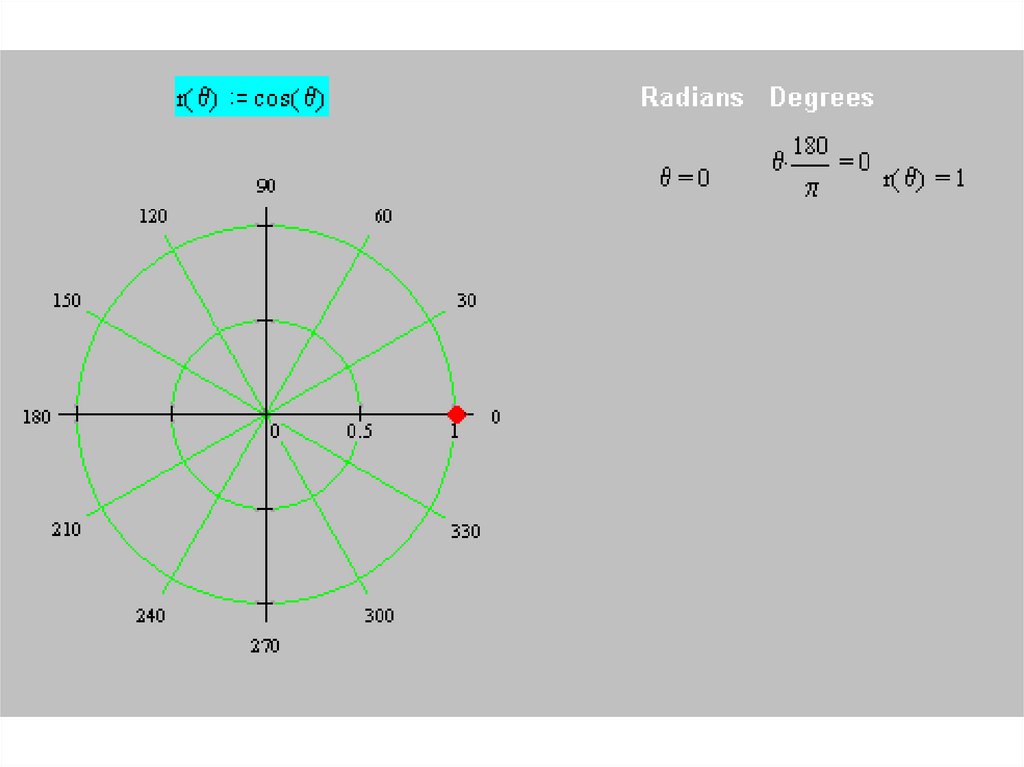
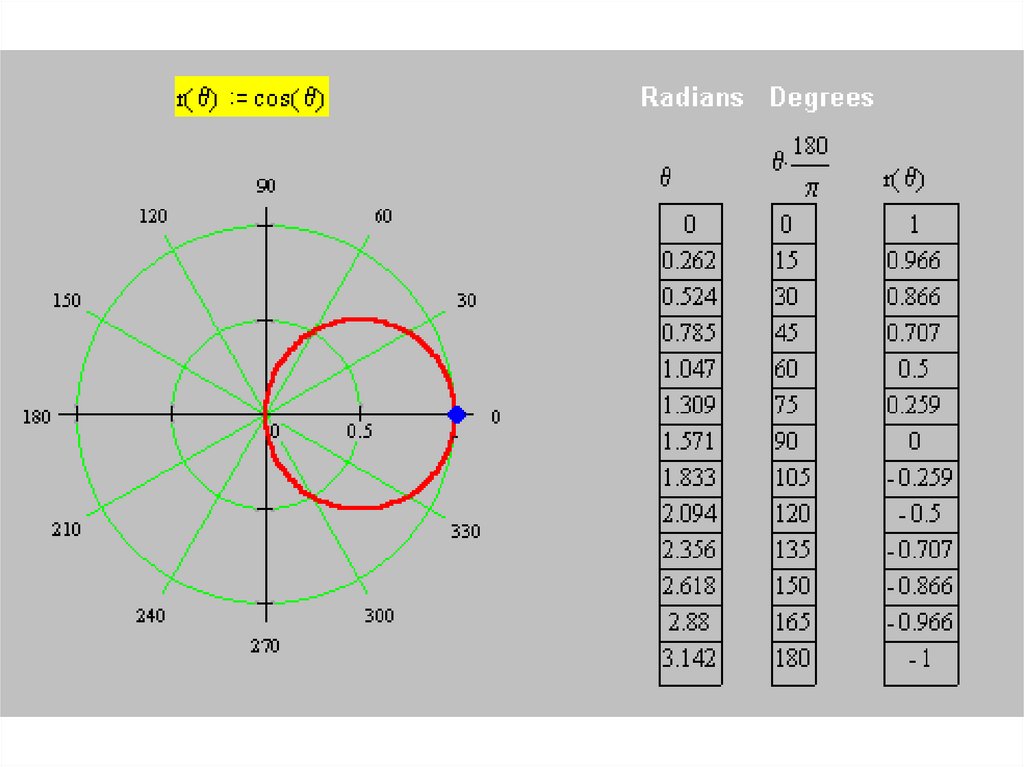
• Построим кривуюr(θ) = cos θ








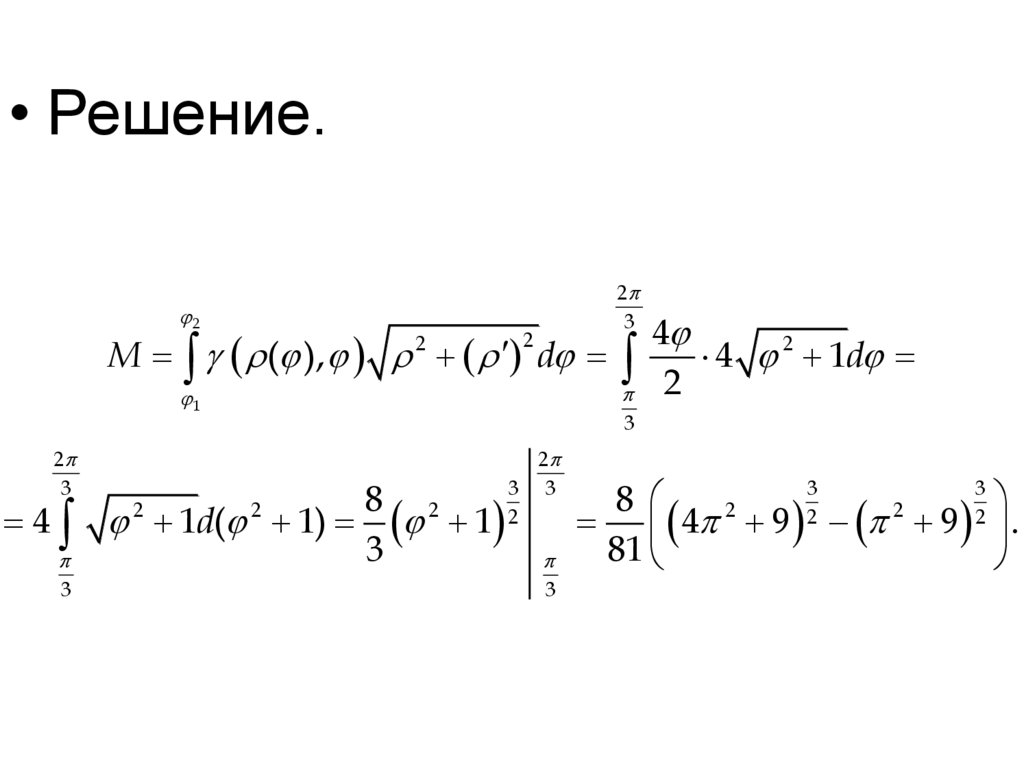


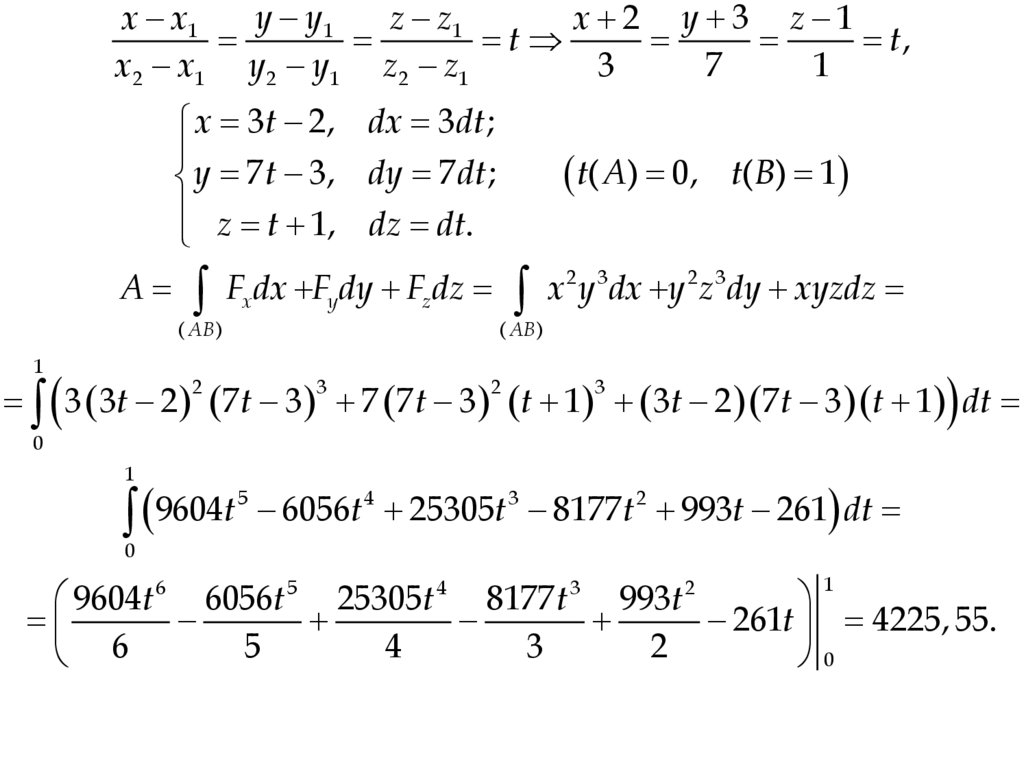

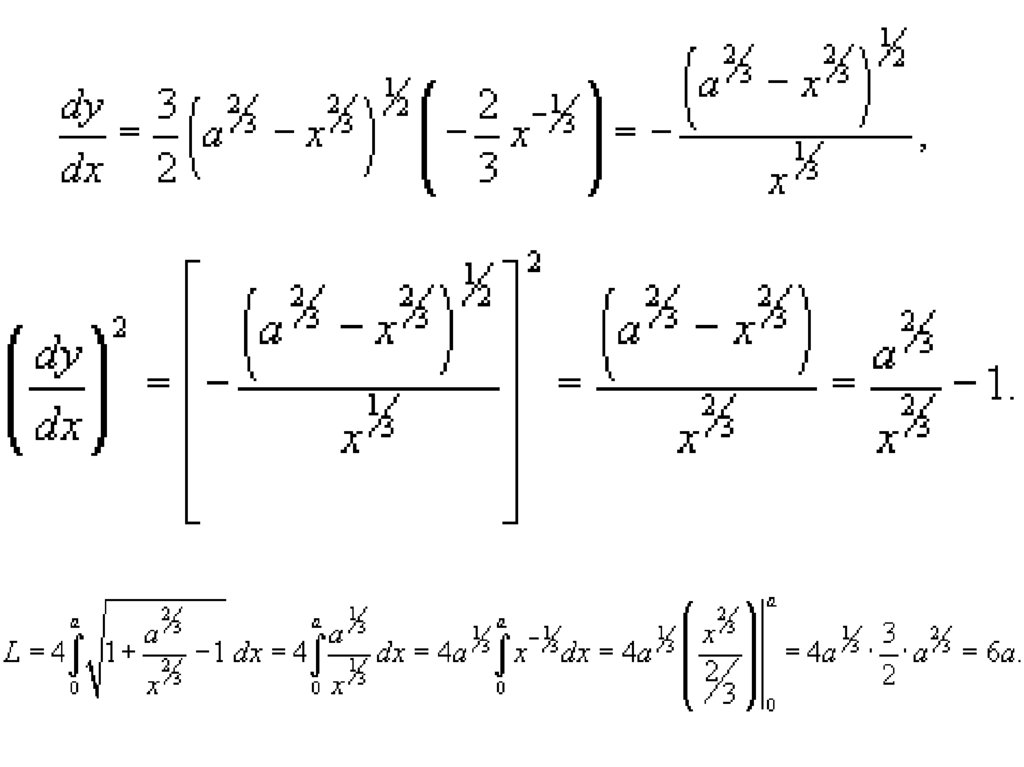


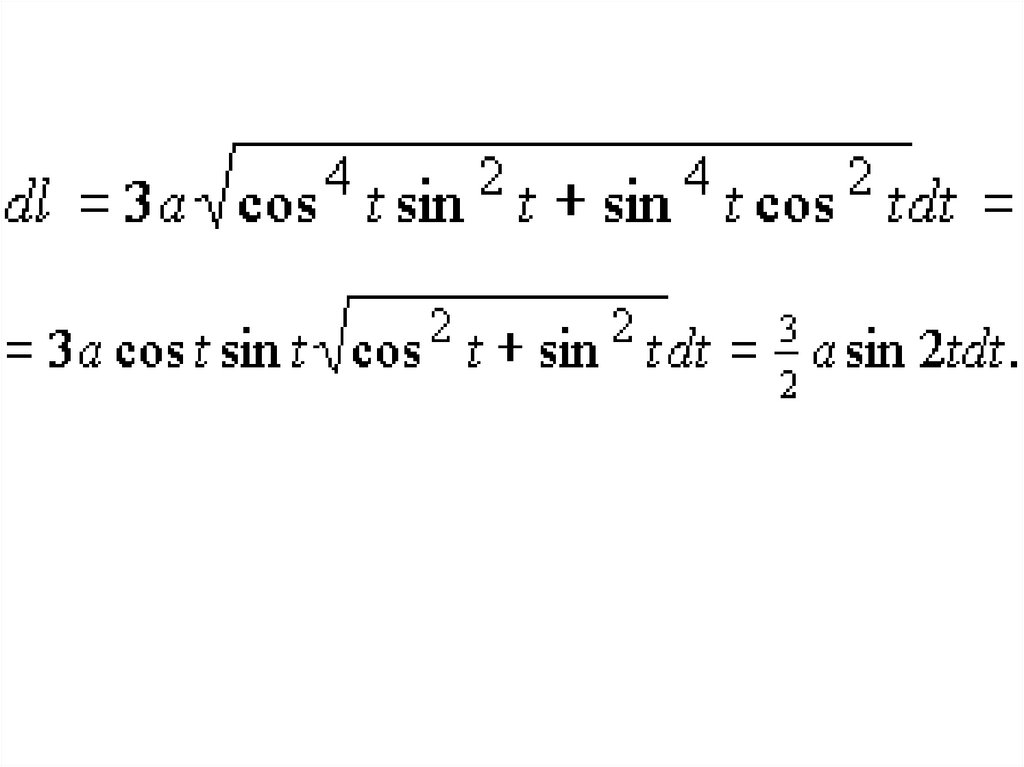



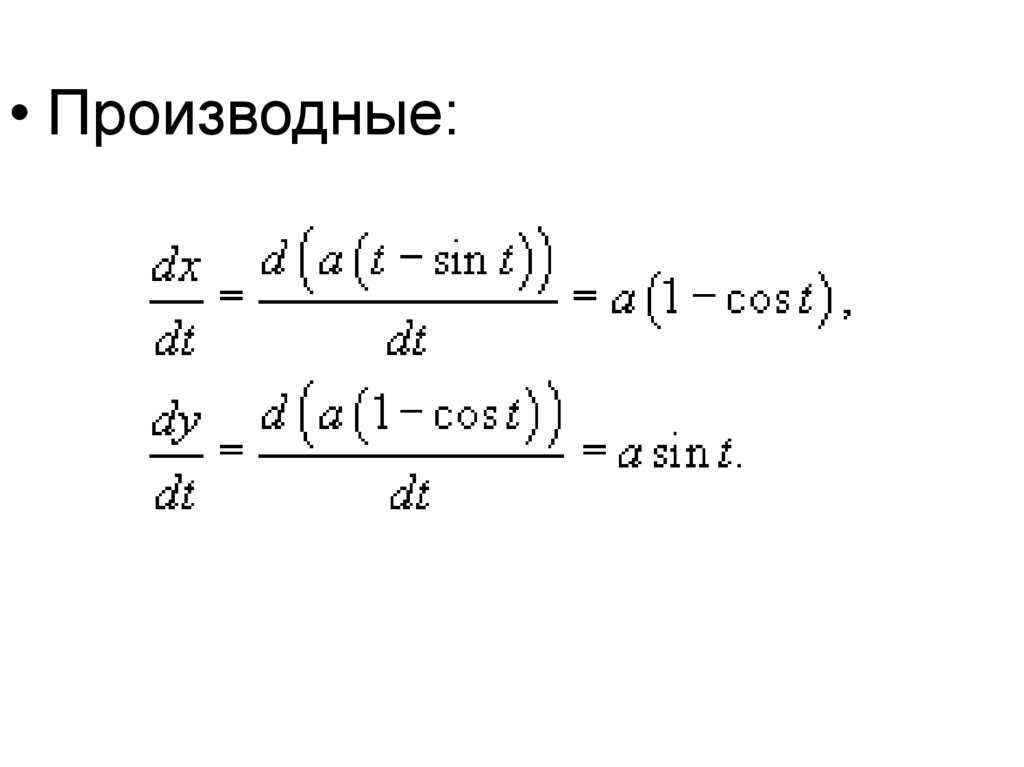




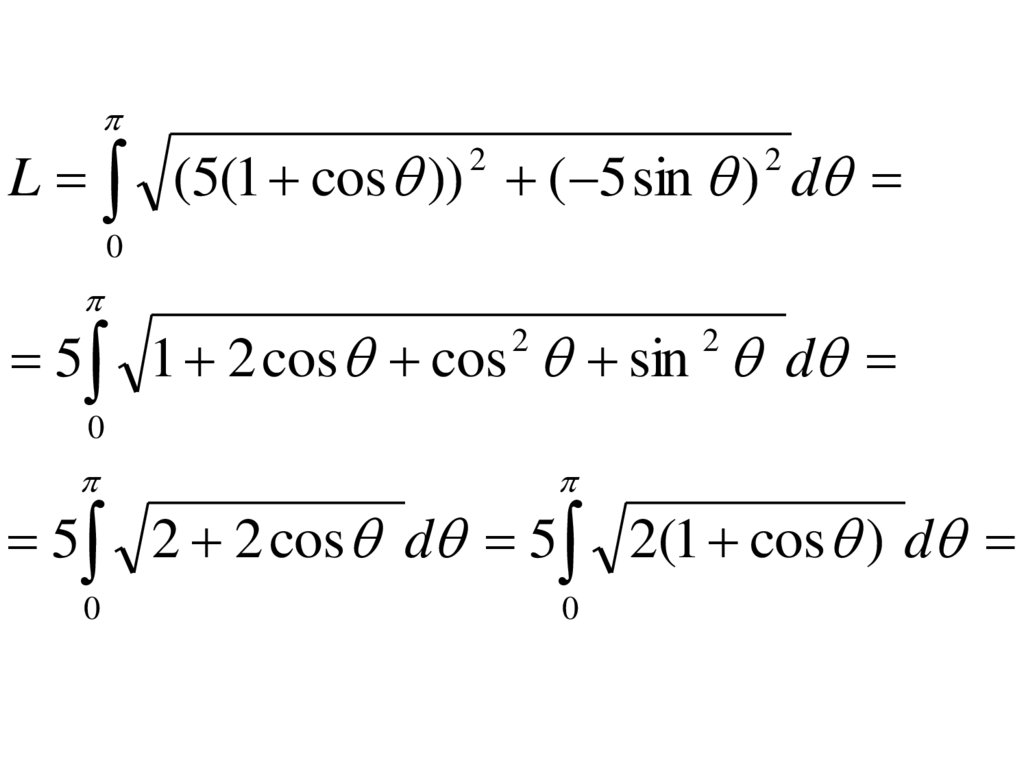

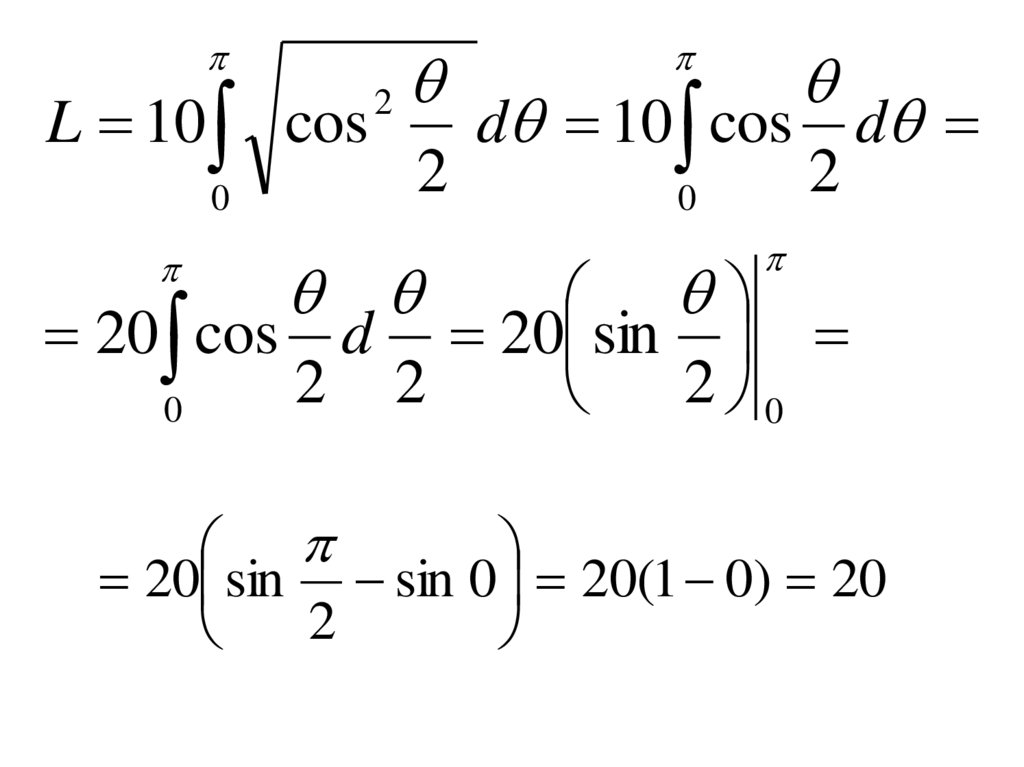



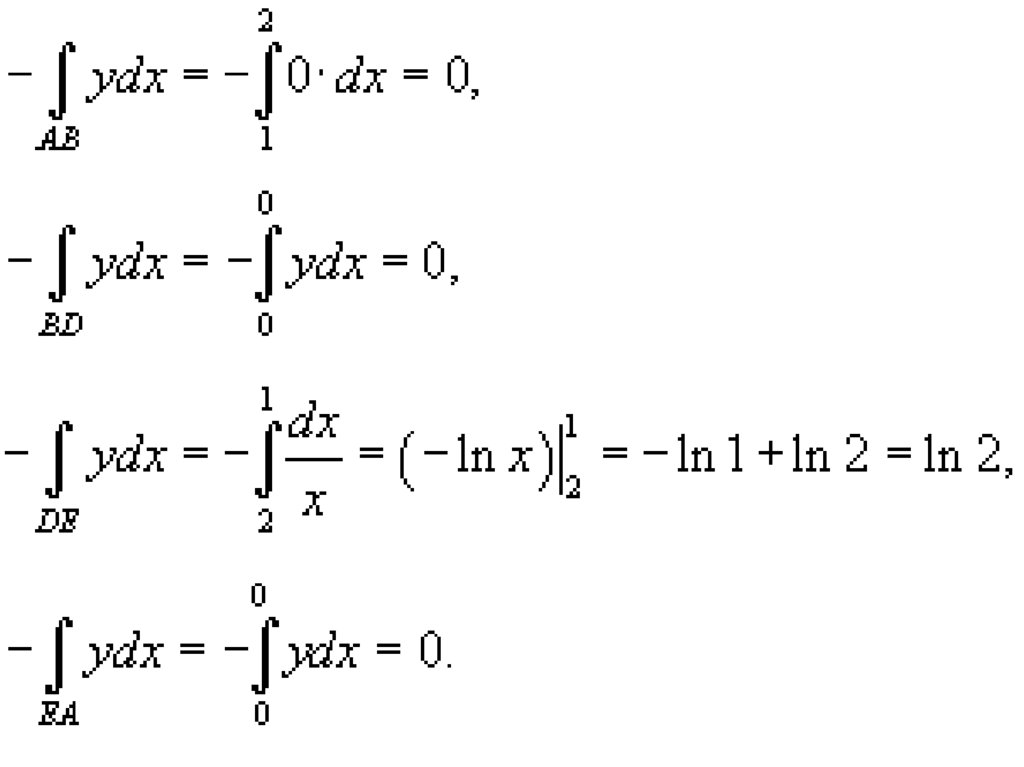



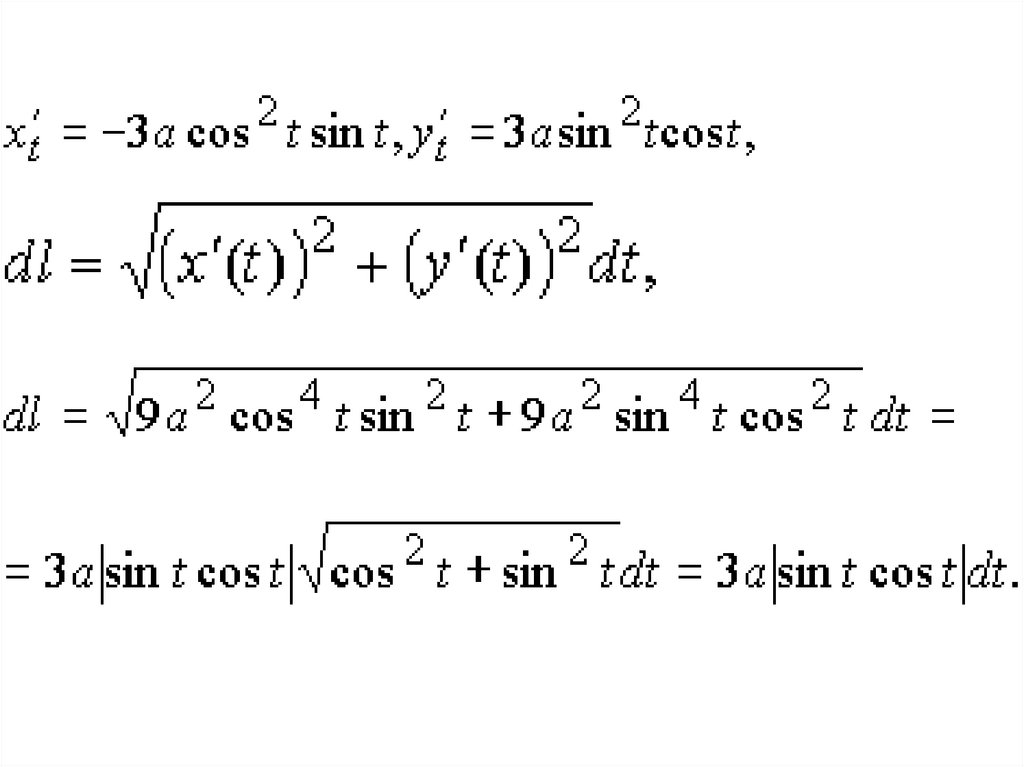

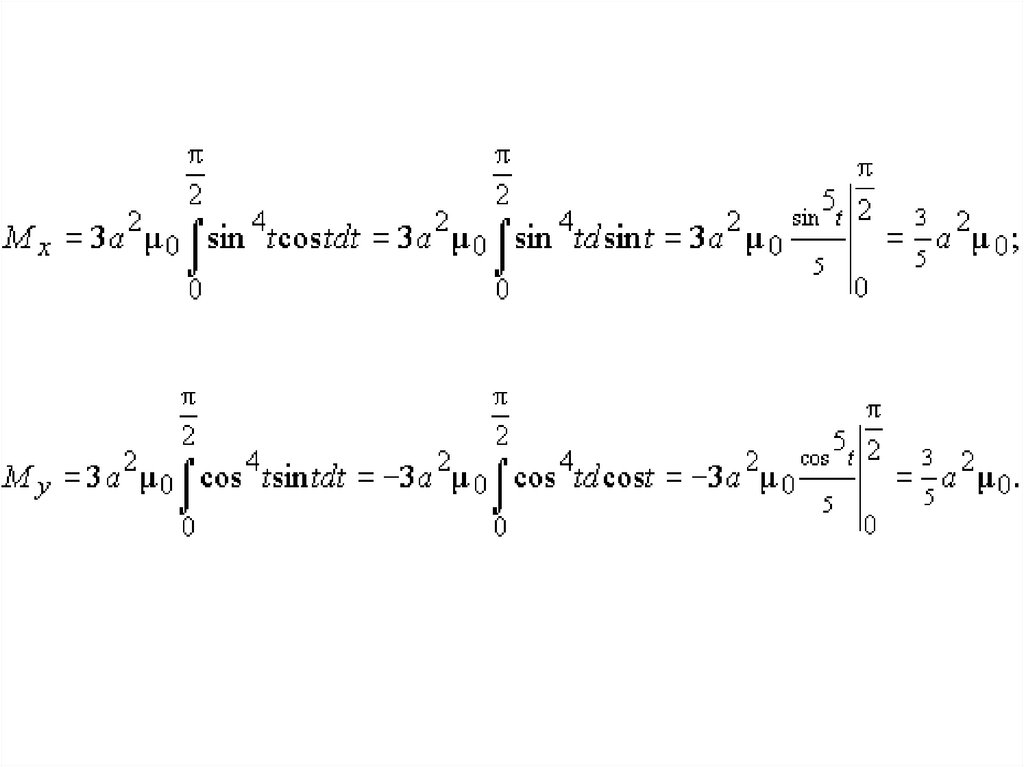



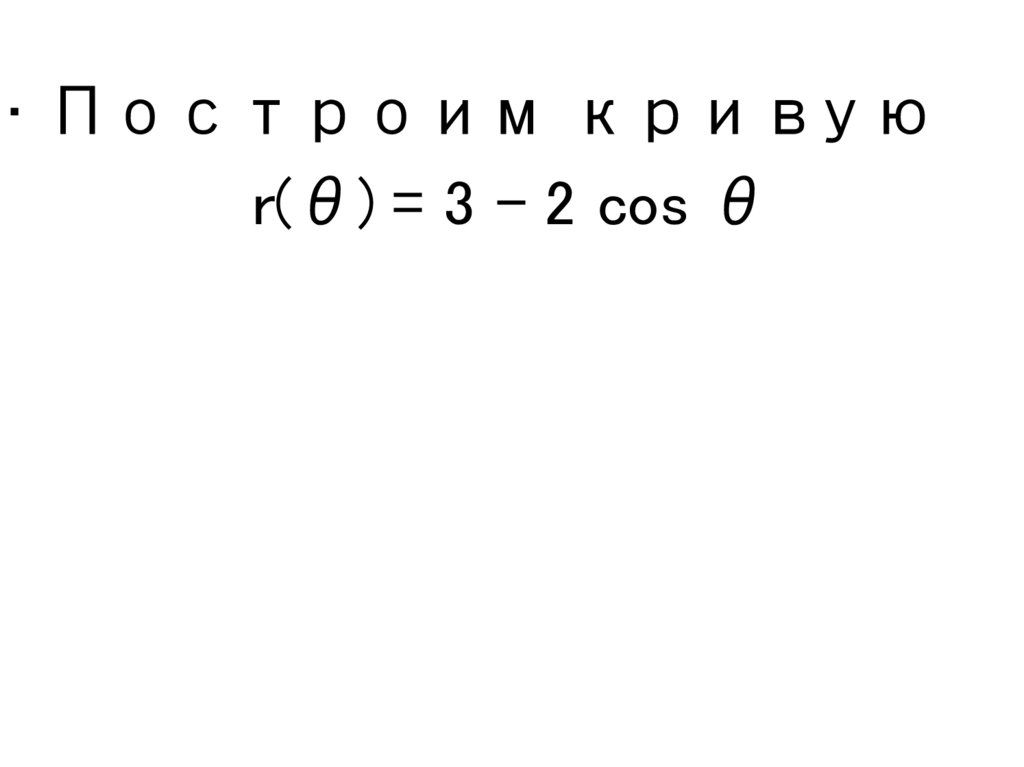
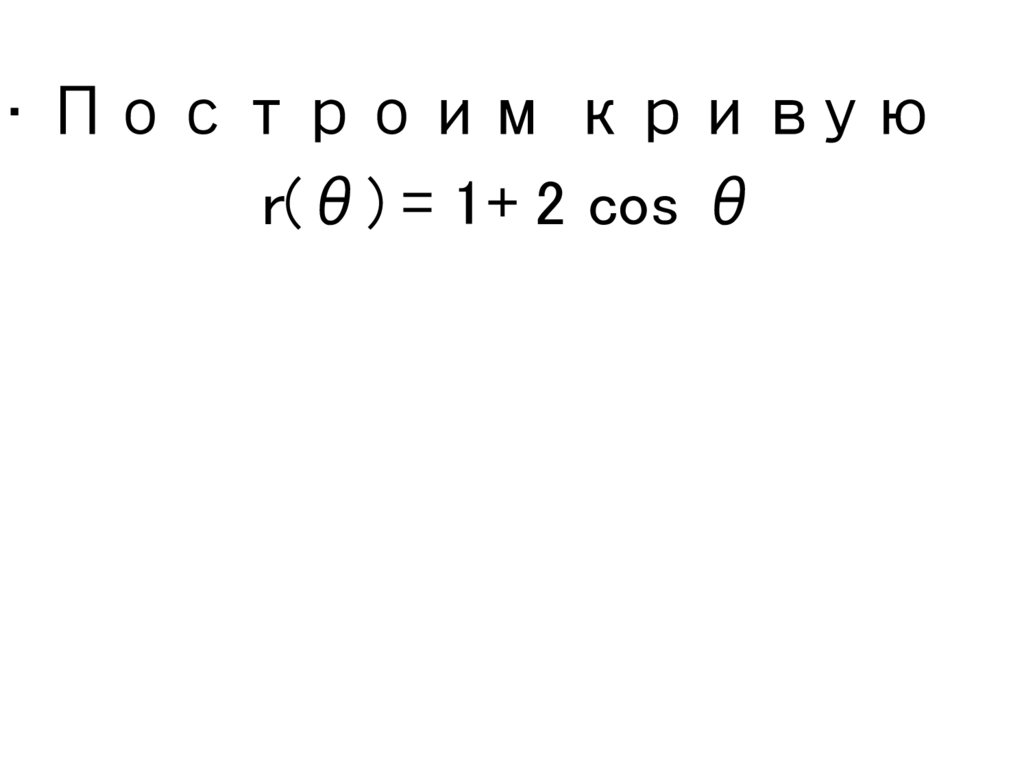

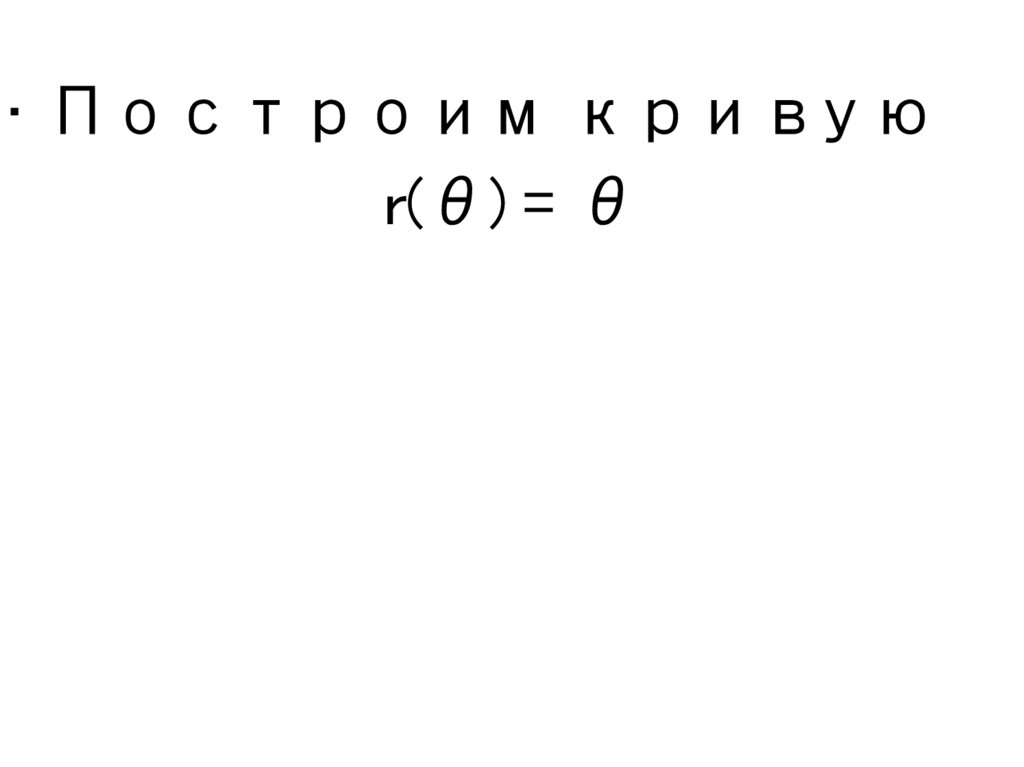


 physics
physics








