Курс лекций по теоретической механике. Динамика (II часть)

1. Курс лекций по теоретической механике

Московский государственный университет путей сообщения (МИИТ)
Кафедра теоретической механики
Научно-технический центр транспортных технологий
Бондаренко А.Н.
Курс лекций по
теоретической
механике
Динамика (II часть)
Электронный учебный курс написан на основе лекций, читавшихся автором для студентов,
обучавшихся по специальностям СЖД, ПГС и СДМ в НИИЖТе и МИИТе (1974-2006 гг.). Учебный
материал соответствует календарным планам в объеме трех семестров.
Для полной реализации анимационных эффектов при презентации необходимо использовать средство просмотра
Power Point не ниже, чем встроенный в Microsoft Office операционной системы Windows-ХР Professional.
Запуск презентации – F5, навигация – Enter, навигационные клавиши, щелчок мыши, кнопки.
Завершение – Esc.
Замечания и предложения можно послать по e-mail: [email protected] .
Москва - 2007

2. Содержание

Лекция 9. Работа, мощность силы. Кинетическая энергия. Теоремы об изменении кинетической энергии для
материальной точки и системы. Пример решения задач на использование теоремы об изменении кинетической
энергии материальной точки.
Лекция 10. Пример решения задач на использование теоремы об изменении кинетической энергии системы.
Потенциальное силовое поле. Силовая функция. Потенциальная энергия системы. Закон сохранения механической
энергии.
Лекция 11. Динамика поступательного и вращательного движения твердого тела. Физический маятник.
Динамика плоского движения твердого тела. Принцип Даламбера для материальной точки и механической системы.
Приведение сил инерции точек при поступательном и вращательном движениях. твердого тела.
Лекция 12. Пример приведения сил инерции при вращательном движении тела. Приведение сил инерции точек при
плоском движении твердого тела. Определение динамических реакций подшипников при вращении твердого тела.
Балансировка.
Лекция 13. Аналитическая механика. Обобщенные координаты. Уравнения связей. Возможные перемещения.
Идеальные связи. Принцип возможных перемещений. Примеры использования принципа возможных перемещений
при определении реакций связей.
Лекция 14. Общее уравнение динамики. Пример решения задачи на применение общего уравнения динамики.
Обобщенные силы.
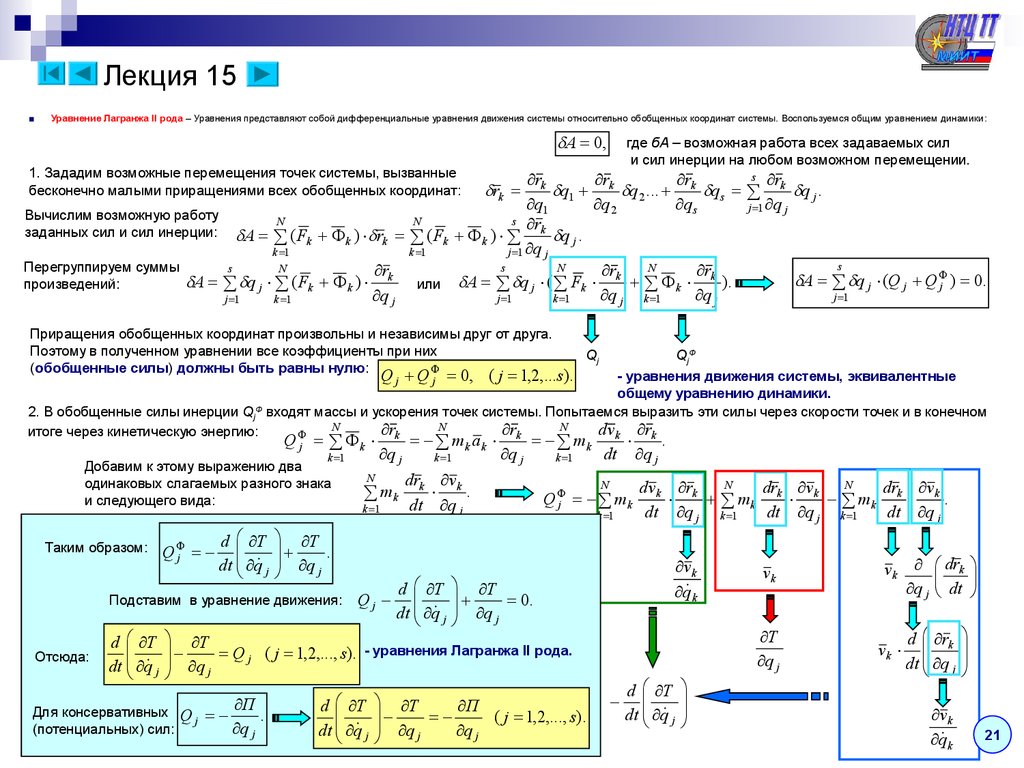
Лекция 15. Уравнение Лагранжа II рода. Кинетический потенциал. Пример решения задачи на применение
уравнения Лагранжа II рода. Вариационный принцип Гамильтона-Остроградского. Понятие об устойчивости
состояния равновесия системы в потенциальном поле.
Лекция 16. Малые колебания систем с несколькими степенями свободы. Общая форма дифференциальных
уравнений колебаний. Прямая форма. Обратная форма. Главные координаты. Свободные колебания с учетом
сопротивления среды.
Лекция 17. Элементарная теория удара. Общие теоремы теории удара. Удар тела о неподвижную преграду. Случай
косого удара. Гидравлический удар в трубах. Прямой центральный удар двух тел.
Рекомендуемая литература
1. Яблонский А.А. Курс теоретической механики. Ч.2. М.: Высшая школа. 1977 г. 368 с.
2. Мещерский И.В. Сборник задач по теоретической механике. М.: Наука. 1986 г. 416 с.
3. Сборник заданий для курсовых работ /Под ред. А.А. Яблонского. М.:Высшая школа. 1985 г. 366 с.
4. Бондаренко А.Н. “Теоретическая механика в примерах и задачах. Динамика” (электронное пособие
www.miit.ru/institut/ipss/faculties/trm/main.htm ), 2004 г.

3. Лекция 9

Работа, мощность силы. Кинетическая и потенциальная энергия – механическое движение в результате взаимодействия
механических систем может переноситься с одной механической системы на другую:
1.
без превращений в другую форму движения, т.е. в качестве того же механического движения,
2.
с превращением в другую форму движения материи (потенциальную энергию, теплоту, электрическую энергию и т.д.)
Каждый из этих случаев имеет свои измерители (меры) механического движения и механического взаимодействия, отстаиваемые в свое
время Декартом и Лейбницем (см. таблицу):
Ф. Энгельс показал существование и равноправность
Мера механического движения
Мера механического
обоих (векторных и скалярных) мер движения, каждой
взаимодействия
из которых соответствуют свои меры механического
взаимодействия.
Декарт
Количество движения
Q mv Импульс силы S F dt
Импульс силы является мерой действия силы при
изменении механического движения.
Работа является количественной мерой превращения
Лейбниц
Кинетическая энергия
mv 2 Работа силы
A F ds
T
механического движения в какую-либо другую форму
2
движения материи.
Работа силы, приложенной к материальной точке – Пусть точка приложения переменной по величине и направлению силы перемещается по некоторой
произвольной траектории. На малом (элементарном) перемещении силу можно считать постоянной и элементарная работа силы равна проекции силы на
направление перемещения (касательную к траектории движения), умноженной на элементарное перемещение :
0 s
ds
M
F
v
T
2
2
Знак элементарной работы определяется
величиной угла и знаком cos :
бA F ds F cos ds
Поскольку часто более удобно работать с острыми углами, то в этом случае
используют острый угол и знак присваивают по следующему простому
правилу: если сила и перемещение совпадают по направлению,
то присваивается знак +, если противоположны по направлению, то знак .
Элементарная работа может быть записана в виде скалярного произведения:
Работа на конечном перемещении M M1 получается
суммированием или интегрированием:
A бA
M1
A F ds
Частные случаи: 1. Сила постоянная по величине (F = const)
и направлению ( =const):
2. Сила постоянная по величине (F = const)
и параллельна перемещению ( =0):
M
бA F dr
и в проекциях:
бA 0;
бA 0.
бA Fx dx F y dy Fz dz.
M1
M1
A Fx dx F y dy Fz dz.
A F dr
M
M
M1
M1
M
M
A F cos ds F cos ds Fs cos .
A Fs.
3. Сила перпендикулярна перемещению:
A 0
1

4. Лекция 9 (продолжение – 9.2)

Можно доказать следующие теоремы и утверждения:
Работа равнодействующей на некотором перемещении равна алгебраической сумме работ составляющих сил на том же
перемещении:
M1
M1
M1
M1
A Ai
A R dr ( F1 F2 ...) dr F1 dr F2 dr ... A1 A1 ... Ai
M
M
M
M
■
Работа постоянной сил по величине и направлению на составном перемещении равна алгебраической сумме работ этой силы
на каждом из составляющих перемещений:
A Asi
A F s F ( s1 s 2 ...) F s1 F s 2 ... As1 As 2 ... Asi
Ai 0
M1
M1
A ( R R ) dr ( R R ) dr 0;
■
Работа внутренних сил неизменяемой системы равна нулю:
■
Работа силы тяжести не зависит от вида траектории и равна произведению силы тяжести на разность высот:
i
M
M1
M1
M
M
M
A Gx dx G y dy Gz dz ( G )dz Gz z1 G ( z1 z ); (Gx G y 0, Gz -G)
■
Работа линейной силы упругости (реакции пружины)
при перемещении из состояния равновесия:
z
( R ' R ).
'
A G ( z1 z )
z
2
Δx
A c
.
2
M1
M1
x2
A Rx dx ( cx)dx c
2
M
M
x1
x 0
x12
c ; ( Rx cx)
2
Работа силы, приложенной к твердому телу, вращающемуся вокруг неподвижной оси. Запишем выражение для
элементарной работы силы, приложенной к точке, и выразим элементарное перемещение через угол поворота тела:
бA F ds F cos ds F cos R d
бA Fh d M z ( F )d .
ω
R
h
Работа силы, приложенной к вращающемуся твердому телу,
для конечного угла поворота:
h
F
d
R
ds
В частном случае постоянного значения момента силы относительно оси
работа равна произведению момента силы на угол поворота:
F
-работа силы, приложенной
к вращающемуся твердому
телу, выражается через
момент силы относительно
оси.
1
A M z ( F )d .
A M z ( F )( 1 ).
Мощность – величина, характеризуемая количеством работы, произведенной в единицу времени:
T
A F ds
N
F v F v .
dt
dt
Мощность силы, приложенной к точке:
Мощность силы, приложенной к вращающемуся твердому телу:
N
A M z d
M z z M .
dt
dt
N
A
.
dt
2

5. Лекция 9 (продолжение – 9.3)

Кинетическая энергия – характеризует способность механического движения превращаться в эквивалентное количество другого
движения:
■
Кинетическая энергия
материальной точки:
mv 2
T
2
■
■
Кинетическая энергия твердого тела
при поступательном движении:
MvC2
T
2
■
Кинетическая энергия твердого тела
при вращательном движении:
I 2
T z z
2
■
Кинетическая энергия
твердого тела при плоском
движении:
T
mk vk2
T
2
Кинетическая энергия
системы материальных точек:
MvC2 I zC z2
2
2
mk vk2 v 2
T
2
2
v2
MvC2
mk 2 M 2 ;
mk vk2
mk ( z hk ) 2 z2
T
2
2
2
(v1 v2 ... v vC )
I z z2
m h 2 ;
2
k k
( I z mk hk2 )
mk vk vk
m (v v ) (vC vkC ) MvC2
m v2
k C kC
vC mk vkC k kC .
2
2
2
2
2
dr
d
I zC z
vC mk kC vC ( mk rkC ) 0; ( mk rkC 0)
dt
dt
2
T
Теорема об изменении кинетической энергии материальной точки – Изменение кинетической энергии точки равно работе
сил, действующих на точку на том же перемещении:
Проинтегрируем полученное соотношение:
Запишем основной закон динамики точки:
ma F R
v
Выразим ускорение через скорость и умножим
левую и правую части соотношения скалярно
на дифференциал радиуса-вектора :
m
i
dv
dr R dr
dt
или mv dv R dr .
A
v0
После подстановки пределов получаем:
mv 2
v v
md
d
2
2
mv 2 M
mv 2
d
dA
;
2 M
2
0
dA
mv 2 mv02
A
2
2
Теорема об изменении кинетической энергии системы – Изменение кинетической энергии системы равно работе сил,
действующих на систему на соответствующих перемещениях точек системы:
Запишем теорему об изменении кинетической энергии для произвольной точки системы,
при этом выделим работу внешних и внутренних сил, приложенных к данной точке:
mk vk2
mvk20
Aki Ake .
Просуммируем левые и правые части соотношений:
2
2
В левой части получили разность кинетических энергий системы:
T T0 Aki Ake .
mk vk2 mvk20
Aki Ake .
2
2
Для неизменяемой системы:
T T0 Ake ;
A
i
k
0
3

6. Лекция 9 (продолжение – 9.4)

Пример решения задачи на применение теоремы об изменении кинетической энергии для материальной точки – Снаряд массы m выбрасывается
пружинным устройством из канала под углом к горизонту. Длина нерастянутой пружины жесткостью c равна длине канала l0. Перед выстрелом пружина сжимается
на величину d. Определить скорость снаряда при вылете из канала, а также максимальную высоту полета.
Дано: , c, d, m, l0
Найти: v1, H
N
v2
v1
d
R
G
H
Начальная скорость снаряда равна нулю: v0
Работа сил, приложенных к объекту, равна:
1. Выбираем объект - снаряд
2. Отбрасываем связи – ствол, пружину
A AN AG AR .
3. Заменяем связи реакциями – N, R
Работа нормальной реакции равна нулю (направление
реакции перпендикулярно перемещению): AN 0.
4. Добавляем активные силы – G
Работа силы тяжести:
AG G h mgd sin .
Работа упругой реакции пружины
(направление реакции совпадает
с перемещением):
mv12
Подставляем определенные
0 mgd sin
величины в теорему:
2
5. Записываем теорему об изменении
кинетической энергии для точки:
G
Определяем максимальную высоту полета
(повторяем шаги 1-5):
2
2
mv2 mv1
A
2
2
0.
mv12 mv02
A
2
2
Отсюда величина скорости вылета снаряда:
Вертикальная скорость снаряда в наивысшей точке траектории равна нулю :
v2 y 0.
v1
c
d2
,
2
d2
.
2
cd 2
2 gd sin .
m
Горизонтальная скорость снаряда постоянная (из закона
сохранения проекции на ось x количества движения точки)
и равна:
2
AG G h mg ( H l0 sin ).
cd 2
cd 2
Подставляем определенные
m
2 gd sin cos 2 m
2 gd sin
m
величины в теорему:
m
mg ( H l sin ).
0
2
2
После некоторых сокращений и
Отсюда максимальная
cd 2
(
gd sin ) sin 2 g ( H l0 sin ).
преобразований:
высота полета:
2m
Работа силы тяжести:
AR c
v2 x v1x
H (
cd
2 gd sin cos .
m
cd 2
d sin ) sin 2 l0 sin .
2mg
Заметим, что предыдущее выражение можно более быстро получить,
записывая теорему об изменении кинетической энергии только для
вертикальной скорости движения точки, поскольку горизонтальные силы
отсутствуют и горизонтальная скорость не изменяется..
4

7. Лекция 10

Пример решения задачи на применение теоремы об изменении кинетической энергии для системы – Массивный бумажный
рулон радиуса R, приведенный в движение толчком, катится без проскальзывания по инерции вверх по наклонной шероховатой
плоскости под углом к горизонту с некоторой начальной скоростью. Коэффициент трения качения fk. Определить начальную скорость
рулона, необходимую для того, чтобы он мог перевалить через вершину высотой H от начального положения.
Дано: , fk, H, R
Найти: v0
s
N
Fтр
1. Выбираем объект - рулон
2. Отбрасываем связи – опорную плоскость
v
Mк
H
G
Подставляем определенные
величины в теорему:
3MvC2 0
H
MgH f к Mg cos
,
4
R sin
После некоторых сокращений и
преобразований получаем:
vC 0
4
ctg
gH (1 f к
).
3
R
Кинетическая энергия на вершине
равна нулю:
T 0.
Кинетическая энергия
в начальный момент времени
равна:
MvC2 0 I zC z20
2
2
4. Добавляем активные силы – G
MR 2
Момент инерции массы сплошного
I zC
5. Записываем теорему об изменении
цилиндра равен:
2
vC 0
кинетической энергии для твердого тела:
Угловая
скорость
равна:
z
0
R 2
T T0 Ae
Тогда кинетическая энергия
MvC2 0 1 MR 2 vC 0
3MvC2 0
T
.
0
в начальный момент времени:
2
2 2 R
4
Работа сил, приложенных к объекту, равна:
Ae AN AFтр AG AMк .
Работа нормальной реакции равна нулю:
AN 0.
Работа силы трения скольжения равна нулю (приложена в МЦС): AFтр 0.
3. Заменяем связи реакциями – N, Fтр, Mк
T0
AG G h MgH .
Работа момента сопротивления качению: AMк M к ( 0 ).
M к f к N f к G cos f к Mg cos .
Момент сопротивления качению:
s
H
Разность углов поворота рулона:
0
.
R R sin
Работа силы тяжести:
Заметим, что выражение для начальной
скорости не зависит от массы рулона.
Масса рулона, как мера инертности, будет
влиять на величину усилия, которое должно быть приложено к телу, чтобы сообщить ему указанную начальную скорость.
Потенциальное силовое поле
Силовое поле – пространство, в каждой точке которого на материальную точку действуют силы, зависящие от координат точки.
Стационарное силовое поле – действующие силы которого не зависят от времени, F = F(x, y,z) (поле силы тяжести, поле силы упругости).
Нестационарное силовое поле - действующие силы которого зависят от времени, F = F(x, y,z, t) (электромагнитное поле).
5

8.

Лекция 10 (продолжение – 10.2)
■
Потенциальное силовое поле – в котором существует функция, в каждой точке пространства удовлетворяющая соотношениям:
X
U
;
x
Y
U
;
y
Z
U
,
z
где U = U(x, y, z) – силовая функция.
U
(U C )
U
(U C )
X
;Y
Силовая функция определяется с точностью до постоянной:
x
x
y
y
Основные свойства силовой функции:
Элементарная работа силы потенциального поля равна полному дифференциалу силовой функции:
1.
A Xdx Ydy Zdz
;Z
U (U C )
.
z
z
A dU ,
U
U
U
dx
dy
dz. dU .
x
y
z
Полная работа силы потенциального поля не зависит от траектории перемещения точки и равна разности значений
M
M
силовой функции в конечном и начальном положениях:
M
2.
AM 0 M U U 0 ,
z
M 0 ( x0 , y0 , z0 )
M0
M0
M0
U ( x, y , z ) U ( x 0 , y 0 , z 0 ) U U 0 .
Следствие: Работа силы потенциального поля при перемещении точки по замкнутой траектории
равна нулю:
AM 0 M AMM 0 (U U 0 ) (U 0 U ) 0.
F
M ( x, y , z ) y
x
A A U U
Потенциальная энергия системы – функция, характеризующая запас энергии (потенциальной энергии)
в данной точке потенциального силового поля.
Потенциальная энергия равна работе сил потенциального поля, действующих на материальную точку,
при ее перемещении из данного положения в начальное (нулевое). Для системы материальных точек
потенциальная энергия равна сумме работ сил потенциального поля на всех перемещениях точек системы
в начальное положение.
Величина потенциальной энергии в начальном положении принимается равной нулю: П(x0,y0,z0) = 0.
В произвольной точке потенциальная энергия является функцией координат: П(x,y,z).
– связь потенциальной энергии с силовой
Тогда по определению:
П U0 U.
П AMM 0 AM 0 M (U U 0 ) U 0 U .
функцией.
С учетом: П(x0,y0,z0) = 0 соотношение связи можно записать как разность:
U
П
П П U U.
0
0
Таким образом, изменение потенциальной энергии равно
и обратно по знаку изменению силовой функции. Тогда:
Поскольку потенциальная энергия также определена с точностью до постоянной, то работа силы
потенциального поля на перемещении из точки M0 в точку M равна:
AM 0 M U U 0 П 0 П .
X
;
x
x
U
П
Y
;
y
y
U
П
Z
.
z
z
и
A dU
dП .
6

9. Лекция 10 (продолжение 10.3)

Примеры потенциальных силовых полей
Поле силы тяжести. Сила тяжести, работа которой не зависит от траектории, является примером силы, имеющей потенциал – геометрическое место точек пространства, в которых потенциальная энергия постоянна. Проекции
силы тяжести на координатные
оси равны:
z
M 1 ( x1 , y1 , z1 )
M ( x, y , z )
H
G
z
y
■
y
x
M ( x2 , y 2 , z 2 )
П
0;
x
П
Y
0;
y
П
Z
G.
z
X
Последнее выражение есть дифференциальное уравнение, которое легко
решается разделением переменных и интегрированием левой и правой частей:
П dП
G
z
dz
П Gz C.
Эквипотенциальные поверхности (П = const) представляют собой
горизонтальные плоскости. Сила тяжести направлена перпендикулярно
к этим плоскостям в сторону уменьшения значений потенциальной энергии.
AM1M 2 П1 П 2 (Gz1 C ) (Gz 2 C ) G ( z1 z 2 ) GH .
Работа силы тяжести на перемещении из точки M1 в точку M2:
xПоле центральной силы притяжения. Силы тяжести могут считаться параллельными и постоянными по величине только в небольшой области пространства в поле тяготения Земли и эквипотенциальные поверхности могут считаться плоскими только в пределах этой области. В случае рассмотрения силы
притяжения к центру величина силы прямо пропорциональна массе и обратно пропорциональна квадрату расстояния между материальной точкой и центром тяготения O:
z
M ( x, y , z )
P
O
z
r
y
x
y
x
Проекции силы
притяжения
на координатные
оси равны:
m x
;
r2 r
m y
Y P cos( P , y ) k 2 ;
r r
m z
Z P cos( P , z ) k 2 .
r r
X P cos( P , x) k
Полученное выражение есть дифференциальное уравнение,
которое легко решается интегрированием левой и правой частей:
P k
m
r2
Элементарная работа силы притяжения:
A Xdx Ydy Zdz k
m
( xdx ydy zdz ).
r3
d (r 2 ) d ( x 2 y 2 z 2 ), rdr xdx ydy zdz.
Дифференциал
потенциальной энергии:
dП k
mdr
r2
m
dП dU A k 3 rdr .
r
m
П k C.
r
Эквипотенциальные поверхности (П = const) поля центрального тяготения представляют собой сферические поверхности с центром
в точке O. Сила притяжения направлена по нормали к этим поверхностям в сторону уменьшения значений потенциальной энергии.
Закон сохранения механической энергии – При движении механической системы в стационарном потенциальном поле полная
механическая энергия системы остается постоянной.
По теореме об изменении кинетической энергии системы:
T2 T1 Ak П1 П 2 .
Отсюда:
T2 П 2 T1 П1 const.
Сумму кинетической и потенциальной энергий называют полной механической энергией системы.
7

10. Лекция 11

Динамика поступательного и вращательного движений твердого тела – рассмотренные теоремы динамики системы дают дифференциальные уравнения,
описывающие эти два типа движения твердого тела.
Дифференциальные уравнения поступательного движения твердого тела – из теоремы о движении центра масс системы:
M x C R xe ;
M y C R ye ;
M z C R ze .
Дифференциальные уравнения вращательного движения твердого тела вокруг неподвижной оси – из теоремы об изменении
момента количества движения системы:
I M e .
z z
z
Физический маятник – твердое тело, имеющее неподвижную горизонтальную ось вращения, не проходящую через его центр тяжести, и
находящийся под действием только силы тяжести. При отклонении физического маятника от положения равновесия возникает возвращающий
момент от силы тяжести, наличие которого является условием колебательного движения (качания) относительно положения равновесия.
1. Выбираем объект (маятник):
2. Отбрасываем связи (цилиндрические шарниры):
3. Заменяем связи реакциями (суммарные реакции двух шарниров):
z
YO
y
O
Ga
уравнение качаний
- дифференциальное
sin 0.
физического маятника.
Ix
I x M xe Gl sin , где I x ml 2 , G mg.
Рассмотрим математический маятник длиной l:
С
O1
x
Подставим момент инерции
и представим уравнение в виде:
G
z
YO
y
O
XO
l
x
O1
G
I x M xe Ga sin .
Представим уравнение в виде:
a l
XO
4. Запишем дифференциальное уравнение вращения оси x :
g
sin 0.
l
- дифференциальное уравнение качаний
математического маятника.
Поскольку полученные уравнения отличаются лишь коэффициентами, то всегда можно поставить в
соответствие физическому маятнику математический маятник, период качаний которого равен
периоду данного физического маятника. Для этого достаточно приравнять коэффициенты:
Отсюда можно определить приведенную длину физического маятника:
Последнее неравенство
легко доказывается:
l
2
Ix
I ma
I
xC
xC a.
ma
ma
ma
l
Ixg Ix
; l a.
Ga ma
Ga g
.
Ix
l
Точка O1 физического маятника, находящаяся на расстоянии l по прямой OC называется центром качаний маятника.
В случае малых колебаний sinφ φ:
Период
колебаний:
T
Ix
2
2
.
k
Ga
Ga
Ga
0 или k 2 0, где k
.
Ix
Ix
Используя формулу для периода колебаний можно определять опытным путем
моменты инерции тел сложной формы (положение центра тяжести можно найти
методом подвешивания).
8

11.

Лекция 11 (продолжение – 11.2)
Динамика плоского движения твердого тела – Плоское движение может быть представлено как совокупность поступательного движения тела со скоростью
центра масс и вращательного движения вокруг центра масс. Это представление было использовано ранее при вычислении кинетической энергии:
T
MvC2 I zC z2
2
2
Здесь найдем дифференциальные уравнения движения твердого тела. В кинематике уравнения движения плоской фигуры были получены
при использовании в качестве полюса любой произвольной точки. В динамике в качестве полюса выбирают центр масс:
Первые два дифференциальные уравнения, описывающие поступательное движение тела,
найдем, используя теорему о движении центра масс:
e
Третье дифференциальное уравнение, описывающее
вращательное движение тела вокруг центра масс,
найдем, используя теорему об изменении кинетического
момента системы:
MaC R .
dK z
M ze .
dt
xC f1 (t );
M x C R xe Fixe ;
M y C R ye Fiye .
y C f 2 (t );
f 3 (t ).
I z M ze M ize .
Подобным образом с использованием различных теорем динамики могут быть получены соответствующие уравнения при рассмотрении
динамики других более сложных видов движения твердого тела (сферическое, свободное, ударное взаимодействие).
Принцип Даламбера (Германа, Эйлера) – общий метод, при помощи которого уравнениям динамики по форме придается вид уравнений статики. Благодаря простоте этот метод получил широкое
применение во многих прикладных дисциплинах.
Принцип Даламбера для материальной точки. Основное уравнение динамики точки:
Перенесем произведение массы на ускорение в правую часть:
0 Pi ma .
ma Pi .
Получившееся дополнительное слагаемое
имеет размерность силы и принимается за силу
инерции, направленную в сторону
противоположную ускорению:
ma .
R
С введением силы инерции уравнение динамики
Pi 0.
точки принимает вид уравнения равновесия:
Таким образом, геометрическая сумма приложенных к точке сил и силы инерции этой
точки равна нулю. Сила инерции условно добавляется к действующим на точку силам,
образуя взаимно уравновешенную систему сил.
ay
Пример 1: Кабина лифта весом G
G
Определяем реакцию троса: R G G a y G (1
).
поднимается тросом с ускорением a.
g
g
Определить натяжение троса.
ay
Определяем натяжение троса: T R ; T R G (1
).
1. Выбираем объект (кабина лифта).
g
2. Отбрасываем связь (трос) и заменяем реакцией R.
3. Добавляем к действующим силам силу инерции:
a
G
ma .
4. Составляем уравнение равновесия: Yi 0; R G 0.
Сравните ход решения и результат с примером
1 в лекции 2 (стр.3)
9

12.

Лекция 11 (продолжение – 11.3)
l
y
R
an
Пример 2: Груз весом G подвешен на тросе длиной l и движется по круговой траектории в горизонтальной
плоскости с некоторой скоростью. Угол отклонения троса от вертикали равен .
Определить натяжение троса и скорость груза.
1. Выбираем объект (груз).
2. Отбрасываем связь (трос) и заменяем реакцией R.
v2
v2
n ma n ; n m
m
.
x 4. Составляем уравнение равновесия:
l sin
Yi 0; R cos G 0.
X i 0; - R sin 0.
Из первого уравнения определяем
G
G
реакцию троса:
.
Определяем натяжение троса: T R ; T R
R
.
cos
cos
3. Добавляем к действующим силам силу инерции:
G
Подставляем значение реакции троса и силы инерции
во второе уравнение и определяем скорость груза:
G
G v2
sin
0. v
cos
g l sin
-
■
Принцип Даламбера для несвободной механической системы.
Принцип Даламбера для k-той точки:
P R 0.
k
Сложим все n уравнений:
k
k
Pk Rk k 0.
Таким образом, геометрическая сумма
P* R*
главных векторов задаваемых сил,
реакций связи и сил инерции материальных
точек равна нулю.
* 0.
gl sin 2
.
cos
Сравните ход решения и результат с
примером 3 в лекции 2 (стр.4).
Здесь Pk – равнодействующая задаваемых сил, приложенных к точке,
Rk – равнодействующая реакций связей, приложенных к точке,
Фk = - mak – сила инерции точки.
Здесь P* – главный вектор задаваемых сил, приложенных к точке,
R* – главный вектор реакций связей, приложенных к точке,
Ф*– главный вектор сил инерции точек системы.
Умножим уравнение, выражающее принцип Даламбера на радиус-вектор, проведенный из центра O к точке:
Сложим все n уравнений:
rk Pk rk Rk rk k 0.
Таким образом, геометрическая сумма M P M R
O
O
главных моментов задаваемых сил,
реакций связи и сил инерции материальных
точек относительно любого центра равна нулю.
■
M O 0.
rk Pk rk Rk rk k 0.
Здесь MOP – главный момент задаваемых сил относительно центра O,
MOR– главный момент реакций связей относительно центра O,
MOФ– главный момент сил инерции точек системы относительно
центра O.
Приведение сил инерции точек твердого тела к простейшему виду - В динамике за центр приведения принимается обычно центр масс системы. В результате
приведения сил инерции в общем случае получается главный вектор сил инерции и главный момент сил инерции относительно центра масс:
* k mk a k ;
M C M iC
rk mk a k .
10

13.

Лекция 11 (продолжение – 11.4)
■
Главный вектор сил инерции твердого тела – не зависит от выбора центра приведения и для всех типов движения равен:
rC
■
m r ;
k k
M
или MrC mk rk ;
M
d 2 rC
dt
2
m
d 2 rk
dt
2
или MaC mk a k ;
* MaC .
* k m k a k Ma C ;
Приведение сил инерции точек твердого тела при поступательном движении – В случае поступательного движения ускорения всех точек
одинаковы и главный момент сил инерции относительно центра масс равен нулю:
M C M iC
rk mk aC mk rk aC MrC aC 0;
т.к. радиус-вектор центра масс обращается в нуль,
если центр приведения совпадает с центром масс.
Таким образом, силы инерции приводятся к равнодействующей силе, приложенной в центре масс, равной по модулю произведению
массы тела на модуль ускорения его центра масс и направленной противоположно этому ускорению.
■
Приведение сил инерции точек твердого тела при вращательном движении вокруг неподвижной оси – Рассмотрим тело, имеющее плоскость материальной симметрии, перпендикулярной оси
вращения. В этом случае ось вращения является главной осью инерции тела в точке O. Ускорения всех точек, лежащих на одной прямой, параллельной оси вращения геометрически равны.
Поэтому силы инерции симметричных точек относительно плоскости материальной симметрии также равны и их равнодействующая будет лежать в этой плоскости (в точке Mк).
z
Главный вектор сил инерции равен:
ω
ε
O
C
* MaC .
Ускорение центра масс:
aC aC aC ; aC OC 2 4
При выборе центра приведения в точке O главный вектор сил инерции должен быть приложен в этой точке параллельно
вектору ускорения центра масс в противоположную сторону:
В произвольной точке Mк ускорение равно:
aC
Mk
O
aC
C
a k
M z
*
k
Mk
a k a k a k ; a k OM k , a k 2 OM k
Так как линии действия центробежных сил инерции проходят через центр вращения, то главный
момент сил инерции вычисляется как сумма моментов только вращательных сил инерции:
a k
M O k OM k mk OM k2 mk OM k2 I z .
Главный момент сил инерции равен произведению углового ускорения на момент инерции
тела относительно оси вращения и направлен в сторону противоположную угловому
k ускорению:
M z I z . Таким образом, силы инерции приводятся к главному вектору
и главному моменту сил инерции.
Как и в статике, силу и пару можно заменить одной силой, равнодействующей, приложенной в новом центре приведения. Можно показать, что
равнодействующая сил инерции будет приложена в центре качаний. В частном случае, если центр масс лежит на оси вращения, главный вектор
сил инерции обращается в нуль и силы инерции приводятся к паре:
*
MaC 0.
M z I zC .
11

14. Лекция 12

Пример: Однородный стержень OA массы M длиной l, шарнирно подвешенный в точке O к вращающейся оси со угловой скоростью ω, находится
в относительном равновесии под углом к оси вращения. Определить силы инерции и угол .
z
M O
s
O
x
d
*
dФ
aC
ω
y
ds
C
G
Силы инерции в каждой точке стержня пропорциональны осестремительному ускорению, величина которого в
свою очередь пропорциональна расстоянию точки до оси вращения (треугольная эпюра распределения).
Элементарная сила инерции, приложенная к элементарной массе длины ds , расположенной на расстоянии s
от точки О, равна:
d a dm 2 s sin Ads Главный вектор сил инерции находится интегрированием
dФ по длине стержня:
s2
d s sin Ads sin A sds sin A
2
0
0
*
*
l
2
l
2
l
2
Этот же результат можно гораздо проще получить
используя ускорение центра масс:
0
1 2
1
sin Al 2 M 2 l sin .
2
2
* MaC M 2
l
sin .
2
A
Главный момент сил инерции нельзя найти по формуле MФ0 = Ix x, т.к. стержень OA находится в относительном равновесии
и x = x = 0. Однако силы инерции от вращения стержня относительно оси z создают момент сил инерции:
l
l
l
s3
1
2
M zd s cos s sin Ads cos sin A s ds cos sin A
2 cos sin Ml 2 * l cos .
3 0 3
3
0
0
O
2
2
Таким образом, силы инерции приводятся к главному вектору,
приложенному в центре приведения O, и главному моменту
относительно этого центра.
Угол можно определить из уравнения относительного
равновесия:
M
iO
0;
2
l
l cos Mg sin 0
3
2
2
2
Полученную
Таким образом,
систему
равнодействующая
силы и пары можно
силзаменить
инерцииодной силой,
равнодействующей
приложена в центре
сил
тяжести
инерции,
эпюры
приложенной
распределения
в точке,
M O
d
отстоящей
сил инерции.
от центра
Такомуприведения
расположению
по перпендикуляру
соответствует
*
кцентр
направлению
качаний O
силы
на расстоянии:
1.
M 2
l
2
l
sin l cos Mg sin 0
2
3
2
cos
2
l cos .
3
3g
.
2 2l
■
Приведение сил инерции точек твердого тела при плоском движении – Рассмотрим тело, совершающее плоское движение, и имеющее
плоскость материальной симметрии параллельную плоскости движения.
Это движение может быть разложено на поступательное движение с центром масс тела C и вращательное вокруг
подвижной оси zC, проходящей через центр масс тела перпендикулярно плоскости движения.
y
C
* C aC
ε
M zC
zC
xC
В соответствии с этим силы инерции поступательного движения приводятся
к главному вектору сил инерции, приложенному в центре масс,
и главному моменту сил инерции (паре сил, лежащей в плоскости движения):
* MaC .
M zC
I zC .
12

15.

Лекция 12 (продолжение – 12.2)
Определение динамических реакций подшипников при вращении твердого тела вокруг неподвижной оси – Тело произвольной
формы вращается вокруг неподвижной оси z с угловой скоростью ω и угловым ускорением ε.
1. Освобождаем объект движения от связей и заменяем их реакциями:
2. Показываем внешние задаваемые (активные) силы:
z
3. Добавляем к системе сил силы инерции. В каждой точке тела прикладываем вращательную и
B
центробежную силы инерции:
YB
X i 0; M xi 0;
4. Полученная система сил удовлетворяет уравнениям равновесия:
Yi 0;
M уi 0;
5. Силы инерции в общем случае приводятся к главному вектору
и
главному
моменту
сил
инерции.
Определим
величину
и
направление
ω
Z i 0;
M zi 0.
P компонент главного вектора сил инерции:
XB
1
ε
a k
K
O
P2
C
Mk
k
xC
zk
ZA
Pn
* A
XA y
k
O
k
G
x
a k
YA
y
xk
*
y
i
i
*
xi
*
* y M OC sin M xC ;
* MaC .
* x M 2OC sin M 2 xC ; * y M 2OC cos M 2 yC .
Выбираем центр приведения в начале координат и прикладываем компоненты
главного вектора сил инерции в этом центре:
6. Определим компоненты главного момента сил инерции относительно центра
приведения как осевые моменты непосредственным суммированием по каждой
из компонент сил инерции, приложенных в точке:
M x k sin k zk mk rk sin k z k mk xk z k I xz .
M z 0; M z k rk mk rk rk mk rk2 I z .
M x M x 0;
M y M y 0;
zi
M z 0.
k
y
rk
ak
xk
yk
M y k cos k z k mk rk cos k z k mk yk zk I yz .
уi
*
y
C
* x M OC cos M yC ;
M x k cos k z k mk 2 rk cos k z k 2 mk yk zk 2 I yz . K
M y y sin k z k mk 2 rk sin k z k 2 mk xk zk 2 I xz .
*
x
aC
x
X 0; M
Y 0; M
Z 0;
M
*
x
y
C
*
6. Запишем уравнения равновесия
полученной системы сил с учетом
динамических добавок от
возникающих сил инерции:
i
yC
a
* MaC ;
x
Mk
k
X A X B Fkx M yC M 2 xC 0;
YB AB M xi I xz I yz 2 0;
Z A Fkz 0;
M
YA YB Fky M xC M 2 yC 0;
ak
k
X B AB M уi I yz I xz 2 0;
zi
I z 0.
Из первых пяти полученных уравнений можно определить реакции подшипников. Последнее уравнение является дифференциальным
уравнением вращения. Динамические добавки зависят от положения центра масс тела и значений центробежных моментов инерции
этого тела.
13

16.

Лекция 12 (продолжение – 12.3)
■
Балансировка вращающегося тела – Добавление сил инерции к действующим силам есть результат введения подвижной системы координат, связанной с вращающимся телом. Полученные уравнения представляют собой относительные
уравнения равновесия, записанные для этой подвижной системы координат:
z
B
XB
YB
ω
ε
O
C
k
G
x
XA y
k
k
Z A Fkz 0;
M
YA YB Fky M xC M 2 yC 0;
X B AB M уi I yz I xz 2 0;
zi
I z 0.
Из 4 и 5 уравнений системы
определим эти составляющие:
X B
Центробежные моменты инерции, вычисляемые относительно подвижных осей, не изменяются при
вращении тела. Модуль полной дополнительной реакции зависит от угловой скорости и ускорения.
В случае установившегося вращения ( = 0 ), величина полной дополнительной реакции
Pn
пропорциональна квадрату угловой скорости. В современных машинах угловые скорости по величине
y
могут быть значительными, так что дополнительные динамические реакции могут во много раз
превышать статические реакции. Кроме того, направления этой динамической реакции и условно
xk
статической составляющей изменяются по отношению к неподвижной системе координат. Это вызывает
знакопеременное нагружение опорных узлов, приводящее к их усталостному разрушению.
Если центр масс находится на оси вращения, но главная центральная ось инерции тела не совпадает с осью
вращения, то условно статические реакции при консервативных заданных силах не будут изменяться по величине и по
направлению (см. уравнения 1,2), но дополнительные динамические реакции образуют пару сил:
zk
ZA
* A
a k
Mk
YB AB M xi I xz I yz 2 0;
1
1
M yi ; X B
( I xz 2 I yz );
AB
AB
YB YB YB .
1
1
YB
M xi ; YB
( I yz 2 I xz ).
AB
AB
Модуль полной дополнительной
1
2
2
2
2
2
4
динамической реакции равен:
RB ( X B ) (YB )
I xz I yz .
AB
X B X B X B ;
P1
a k
K
P2
Реакции подшипников разложим
на две составляющие, условно
статическую и дополнительную
(динамическую), например:
X A X B Fkx M yC M 2 xC 0;
YA
*
MaC R e Fk R A R A RB RB 0.
RA RB ,
т.к.
F
RA RB 0
по определению условно
статических реакций.
Плоскость действия пары и направления дополнительных реакций вращаются вместе с рассматриваемым телом со всеми вытекающими
отсюда последствиями. При конструировании машин и механизмов необходимо исключить возникновение дополнительных динамических
реакций. Для этого вращающиеся элементы должны иметь нулевые центробежные моменты инерции, т.е. главная центральная ось должна
совпадать с осью вращения.
При изготовлении таких элементов возможны незначительные отклонения в размерах, которые приводят к неуравновешенности
возникающих при вращении сил инерции и возникновению дополнительных динамических реакций на опорные устройства. Для предотвращения
этого выполняется балансировка - введение дополнительных масс, силы инерции которых уменьшают неуравновешенность сил
14
инерции тела, или, напротив, высверливание части материал