Similar presentations:
Физика волновых явлений. (Лекция 1)
1.
Лекция 1. Основные понятия и модели физики волновых явлений1. Волновые явления в природе, примеры из механики,
электродинамики, и квантовой физики
2. Математические модели простейших волновых явлений:
- уравнение гармонического осциллятора, общее решение,
начальные условия, комплексная форма записи решения;
- уравнение гармонического осциллятора с переносом, общее решение;
- волновое уравнение (уравнение Даламбера), общее решение
для плоской и сферической геометрий
3. Плоские гармонические волны:
- тригонометрическая и комплексная формы записи плоской волны;
- фазовая скорость плоской волны и скорость переноса возмущений;
- понятие о дисперсионном уравнении, волны без дисперсии
4. Гармонические сферические и цилиндрические волны
- гармонические сферические волны
- гармонические цилиндрические волны
5. Разложение по плоским волнам
- основные соотношения и определения
- разложение по плоским волнам без дисперсии
2.
22
0 0
2
t
(t , r ) A(r ) cos( 0t ) B(r ) sin( 0t )
(0, r ) 0 (r ),
(0, r ) 0 (r )
t
A(r ) 0 (r ), B(r ) 01 0 (r )
(t , r ) f1 (r ) exp( i 0t ) f 2 (r ) exp(i 0t )
1
f1, 2 (r ) [ 0 (r ) i 01 0 (r )]
2
2
2
u 0 0
r
t
(t , r ) f1 (r ut ) exp( i 0t ) f 2 (r ut ) exp(i 0t )
3.
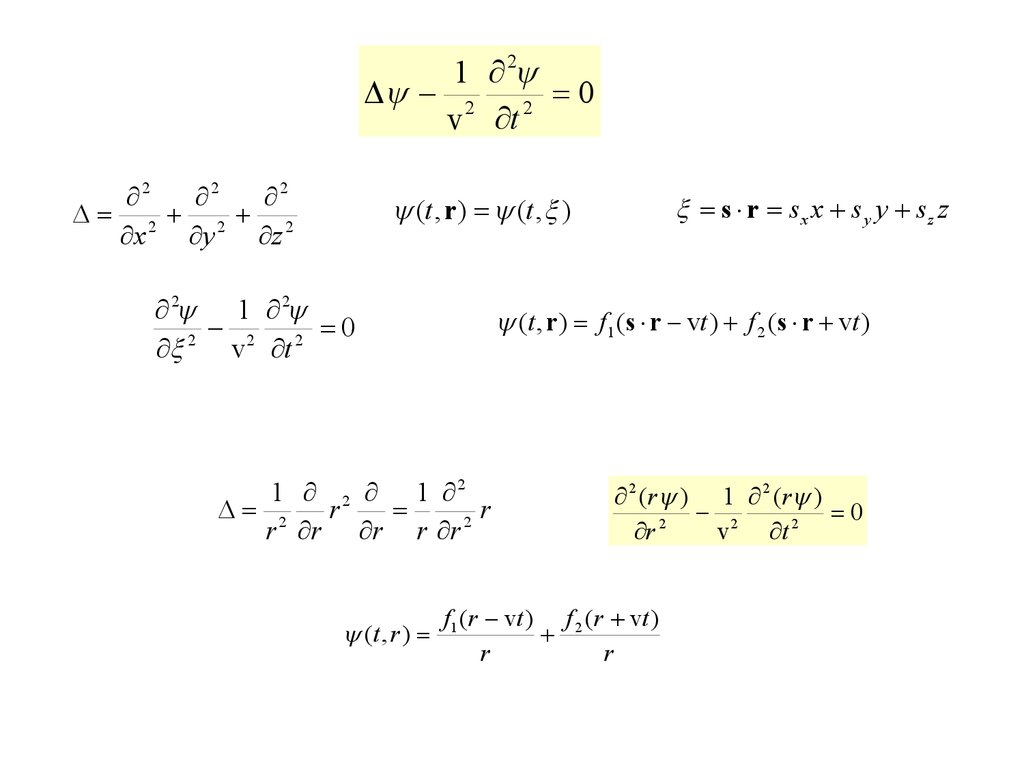
1 22 2 0
v t
2
2
2
2 2 2
x
y
z
s r sx x s y y sz z
(t , r ) (t , )
2 1 2
0
2 v 2 t 2
(t , r ) f1 (s r vt ) f 2 (s r vt )
1 2 1 2
2
r
r
r r r r r 2
(t , r )
2 ( r ) 1 2 ( r )
2
0
r 2
v
t 2
f1 (r vt ) f 2 (r vt )
r
r
4.
(t , r ) A cos( t k r ) B sin( t k r ) C cos( t k r )(t , r ) A cos( t k r ) B sin( t k r ) C cos( t k r )
1
(t , r ) [C0 exp( i t ik r ) C0 exp(i t ik r )]
2
2 20 0
1
(t , r ) [C0 exp( i 0 t ik r ) C0 exp(i 0 t ik r )]
2
( k u) 2 20 k u 0
1
(t , r ) {C0 exp[ik (r u t ) i 0 t ] C0 exp[ ik (r u t ) i 0 t ]}
2
2 k 2 v2
kv
1
(t , r ) {C0 exp[ik (s r vt )] C0 exp[ ik (s r vt )]},
2
t k r const Vф
k cos
D( , k ) 0 (k )
5.
f (r vt ) f 2 (r vt )(t , r ) 1
r
r
f1 (r vt ) A1 cos[k (r vt )] B1 sin[ k (r vt )],
f 2 (r vt ) A2 cos[k (r vt )] B2 sin[ k (r vt )],
(t , r ) (r ) exp( i t )
d 2 (r )
2
k
( r ) 0
2
dr
A
B
(r )
exp(ikr ) exp( ikr )
r
r
1
r
k 2 0
r r r
r 2 k
(t , r )
~ (1)
~H ( 2 ) (kr )
(r ) A
H 0 (kr ) B
0
A
B
(r )
exp(ikr )
exp( ikr )
r
r
f1 (r vt ) f 2 (r vt )
r
r
6.
(t , r )1
(2 ) 3 {C0 (k ) exp[ i (k )t ik r ] C0 (k ) exp[i (k )t ik r ]}dk
2
(0, r ) 0 (r )
1
( 2 ) 3 [C0 (k ) exp(ik r ) C0 (k ) exp( ik r )]dk
2
(k k ) (2 ) 3 exp[i (k k ) r ]dr
(k) V k
1
(t , r ) [ ~0 (r Vt ) exp( i t ) ~0 (r Vt ) exp(i t )]
2
(k ) | k | V kV
(t , r )
C0 (k ) 0 (r ) exp( ik r )dr
C0 (k ) (k x ) (k y )C~0 (k z )
1
(2 ) 3 {C~0 (k z ) exp[ik z ( z Vt )] C~0 (k z ) exp[ ik z ( z Vt )]}dk z
2

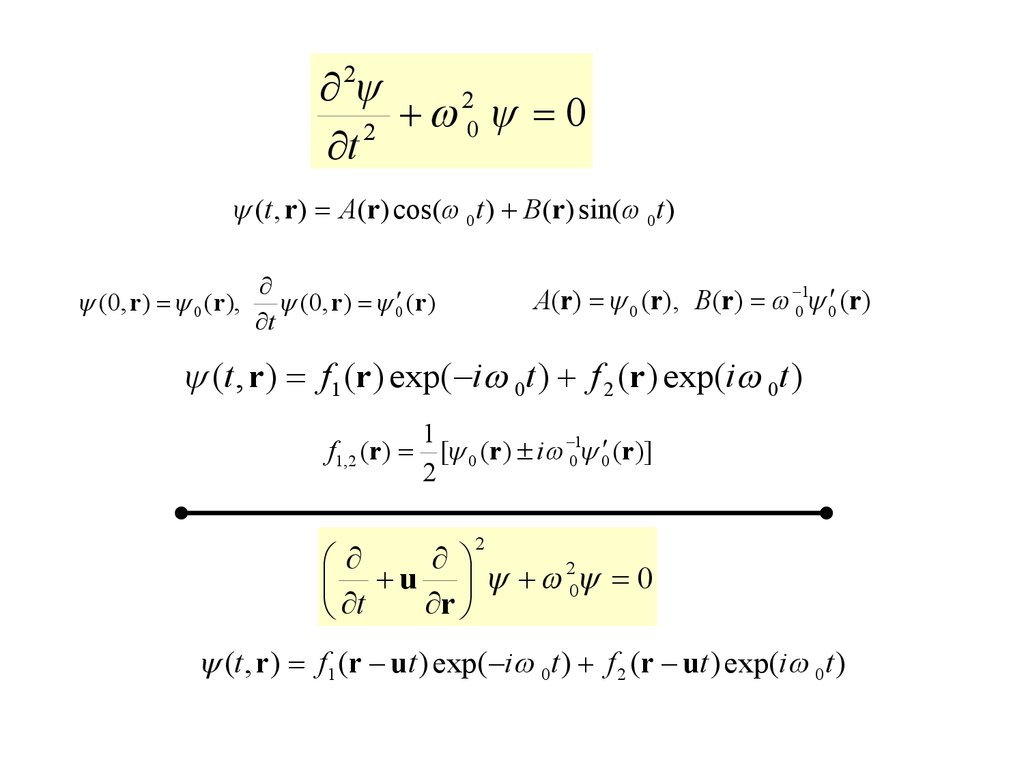

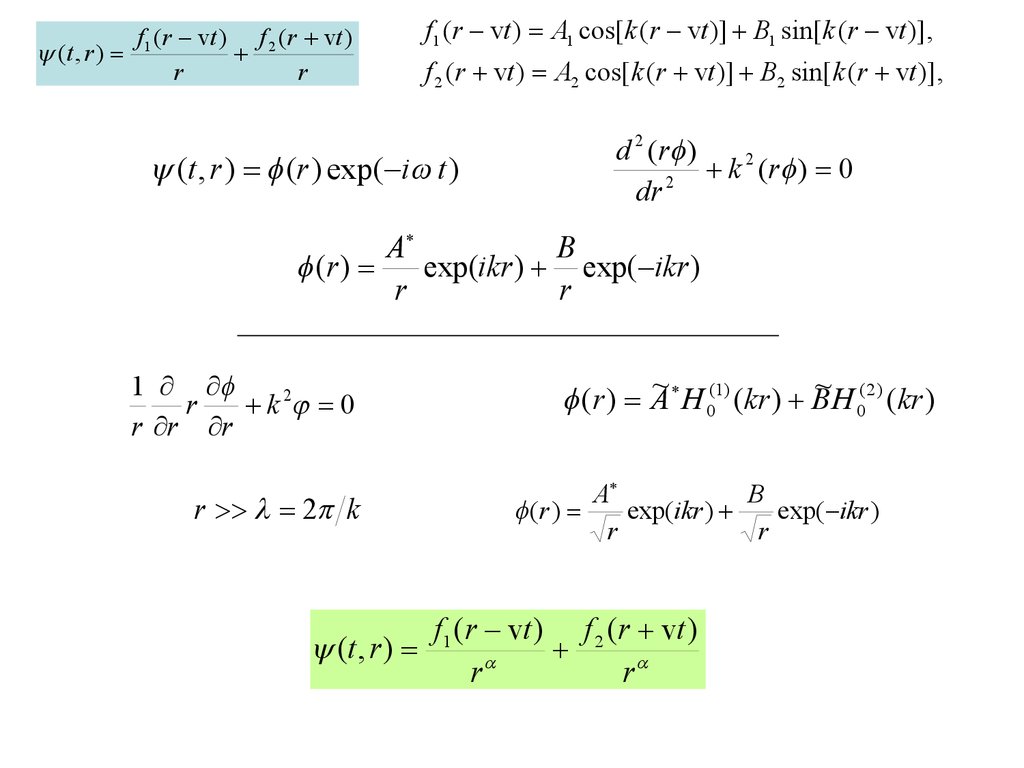

 mathematics
mathematics physics
physics








