Математические методы физики волновых явлений, теория. (Лекция 5)

1.

Лекция 5.
Математические методы физики волновых явлений – теория
1. Общие уравнения для вектора состояния физической системы,
построение дисперсионной функции
2. Задача с начальными условиями. Метод собственных волн
2. Характеристическая функция вектора состояния. Дисперсионный оператор
4. Метод преобразования Лапласа

2.

j
s
Asj
Bsj j 0,
t
z
j 1
n
E x c B y
0
t 0 z
s 1,2, , n
B y
t
c
E x
0
z
1 (t , z ), 2 (t , z ), , n (t , z ) Ψ(t , z )
,
Ψ (t , z ) E x (t , z ), B y (t , z )
Ψ (t , z ) Φ( , k ) exp( i t ikz )
Φ( , k ) 1 ( , k ), 2 ( , k ), , n ( , k )
i s ( , k ) ikAsj Bsj j ( , k ) 0,
n
s 1,2, , n
j 1
D( , k ) det i sj ikAsj Bsj 0, s, j 1,2, , n
m (k ) m 1,2, , n
VФ( m )
m (k )
k
ex ( , k ), by ( , k ) exp( i t ik z )
i e x i c 0 k b y 0
ick ex i by 0
D( , k ) 2 k 2 c02 0
1 kc0 , 2 kc0

3.

n
n
m 1
m 1
Ψ (t , z ) Ψ m (t , z ) Am m (k ) exp i m (k )t ikz
Φ m ( , k ) Φ m ( k ), k Φ m ( k ) 1( m ) ( k ), 2( m ) ( k ), , n( m ) ( k )
(t , z ) E x , B y A 1{ ex(1) , b (1y) } exp ik ( z c0t ) A 2 { ex( 2 ) , b ( 2y) } exp ik ( z c0t )
Am 1( m ) (k ) Am (k )
s( m ) (k ) Ls m (k ), k 1( m ) (k ),
s 2,3, , n
Ψ (t , z ) E x , B y A1{1, 0 } exp ik ( z c0t ) A 2 {1, 0 } exp ik ( z c0t )
m k m k i m k
,
n
n
m 1
m 1
Ψ (t , z ) Ψ m (t , z ) Am m (k ) exp m k t exp i m (k )t ikz
VФ( m )
Re m (k ) m (k )
k
k

4.

1( m ) (k )
(m)
n
n
(k )
Ψ (t , z ) Ψ m (t , z ) Am 2
exp i m (k )t ikz .
m 1
m 1
( m ) (k )
n
,
1( m ) (k ) b1 (k )
(m)
n
2 (k ) b2 (k )
A
m
m 1
( m ) (k ) b (k )
n
n
b1 ( )
b ( )
Ψ (0, z ) 2
exp(i z )
b ( )
n
1
b1 (k )
n
L2 m (k ), k b2 (k )
A
(
k
)
m
m 1
L (k ), k b (k )
n m
n
A1 A2 E0
A1 A2
1
B0
0
1
1
Ex 1
1
1
1
exp ik ( z c0t )
Ψ (t , z ) E0
B0
exp ik ( z c0t ) E0
B0
2
0 0
0 0
By 2

5.

i ,
t
1
(
)
dt
i
,
ik ,
z
1
(
)
dz
ik
.
s n j
Asj
Bsj j f s (t , z ),
t
z
j 1
1
L
(
,
k
)
Ψ (t , z ) 2
A( , k ) exp( i t ik z )
.
L ( , k )
n
s 1,2, , n
,
D( , k ) A( , k ) exp( i t ik z ) 0
(t , z ) E x , B y 1, 0 A( , k ) exp( i t ik z )
c k
2
k 2 c02 A( , k ) exp( i t ik z ) 0
A( , k ) exp( i t ikz ) A(t , z )
ˆ i
, kˆ i
t
z
ˆ 1 i ( )dt , kˆ 1 i ( )dz
1
ˆ
L ( ˆ , k )
D( ˆ , kˆ) A(t , z ) 0
Ψ (t , z ) 2
A(t , z )
L ( ˆ , kˆ)
n
A
(t , z ) E x (t , z ), B y (t , z ) A(t , z ), 0
(t , z )dz
c t
D( ˆ , kˆ) A(t , z ) F (t , z )
2
2
2
2 c0 2 A(t , z ) 0
z
t

6.

( ) (t ) exp(i t )dt
0
( ) i ( ) (t 0)
,
t
(t ) ( )d ( )
0
(n)
n
( q 1) (t 0)
( ) ( i ) ( )
q
(
i
)
q
1
n
i
( )
t
t
0
0
S (t ) 1 ( ) 2 (t ) d 1 (t ) 2 ( ) d S ( ) 1 ( ) 2 ( )
(t )
1
( ) exp( i t )d
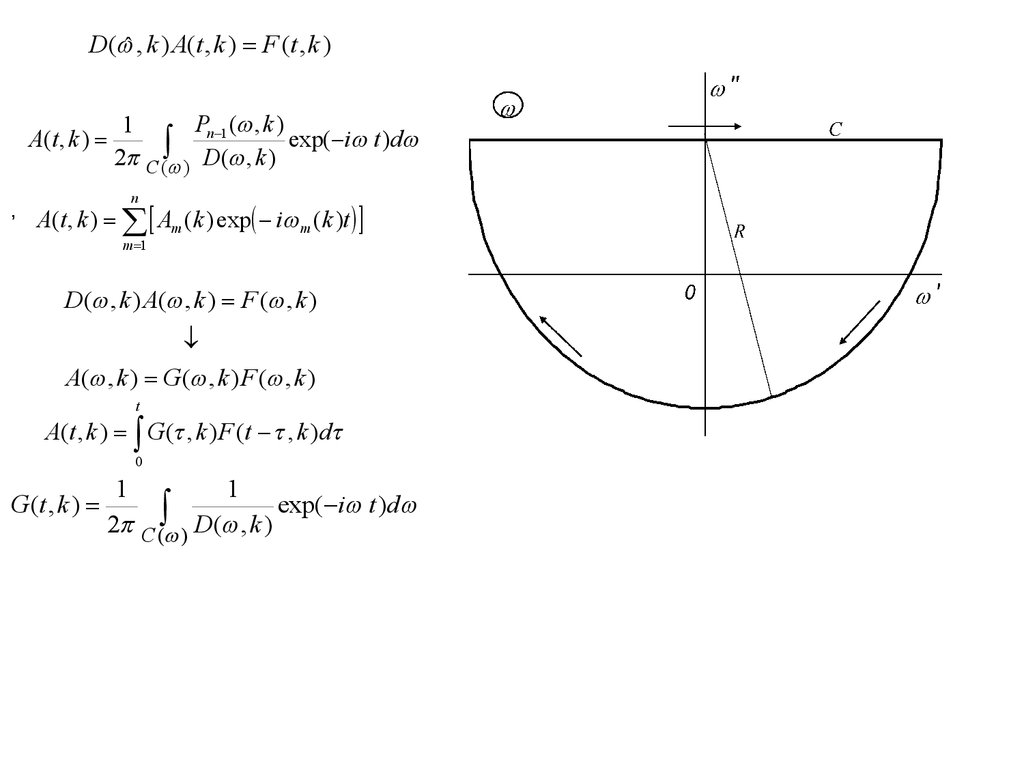
2 C ( )

7.

D( ˆ , k ) A(t , k ) F (t , k )
A(t , k )
,
Pn 1 ( , k )
1
exp( i t )d
2 C ( ) D ( , k )
n
A(t , k ) Am (k ) exp i m (k )t
m 1
D ( , k ) A( , k ) F ( , k )
A( , k ) G ( , k ) F ( , k )
t
A(t , k ) G ( , k ) F (t , k )d
0
G (t , k )
1
1
exp( i t )d
2 C ( ) D( , k )

8.

E x c B y
0,
t 0 z
B y
E
c x 0,
t
z
E (t , z), B (t , z) E (t , k ), B (t , k ) exp(ikz)
x
y
i E x i c 0 k B y E 0 ,
ick E x i B y B0 .
x
y
dB y
dt
E0 kc 0 B0
,
D( , k )
B kcE0
B y ( , k ) i 0
D( , k )
E x ( , k ) i
E0 kc 0 B0
i
exp(
i
t
)
d ,
2 C ( )
( kc0 )( kc0 )
B0 kcE0
i
B y (t , z )
exp(
i
t
)
d ,
2 C ( )
( kc0 )( kc0 )
E x (t , z )
dE x
c
i kB y 0,
dt
0
ickE x 0.