Волны в связанных системах. (Лекция 10)

1.

Лекция 10
Волны в связанных системах
1. Представление связанных осцилляторов
а. Волновод а анизотропной плазмой в представлении
связанных осцилляторов
б. Представление связанных осцилляторов для
магнитоактивной плазмы
в. Представление связанных осцилляторов в общем случае
2. Пучково-плазменная система в представлении связанных осцилляторов
3. Основные уравнения электроники высоких частот
а. Общий вид уравнений. Дисперсионное уравнение
б. Одночастичные и коллективные процессы
в. Метод медленных амплитуд при одночастичных и
коллективных процессах
4. Волны и взаимодействие волн в периодических структурах
а. Поперечные электромагнитные волны в среде с
периодической диэлектрической проницаемостью
б. Обобщение на случай волн произвольной природы
в. Брэгговское отражение

2.

2
2
AP
2
2 c
A
(
t
,
z
)
k
c
,
2 E
t
z
t
2
A
2
2 Le
AP (t , z ) k c E .
t
t
DE ( , k ) 2 k 2 c 2 0,
0 p , k 0 Le c
D p ( , k ) 0.
2
2
Le
0 , | | 0
2
1 2 2
k c 02 1, 2 0
4
2
( 2 k 2 c 2 )( e ) Le
~
~
d
A
dA
~
~
p
E
0 Ap ,
0 AE .
dt
dt
~
AE (t , z ) AE (t ) exp( i 0t ik 0 z ),
~ (t ) exp( i t ik z ).
A (t , z ) A
p
p
A( )
0
~
~
AE (t 0) AE 0 , Ap (t 0) Ap 0
0
A(t ) exp(i t )dt
A(t )
0
~ ( ) A
~ ( ) A ,
i A
E
0 p
E0
~ ( ) A
~ ( ) A .
i A
p
0
E
p0
1
A( ) exp( i t )d
2 C ( )
~ (t ) A cos t A sin t | A | sin( t ),
A
E
E0
0
p0
0
0
0
0
~ (t ) A cos t A sin t | A | cos( t ),
A
p
p0
0
E0
0
0
0
0

3.

~ (t ) exp( i t ik z )
A1 (t , z ) A
1
0
0
~ (t ) exp( i t ik z )
A (t , z ) A
D1 ( ˆ , kˆ) A1 (t , z ) S1 ( ˆ , kˆ) A2 (t , z )
D2 ( ˆ , kˆ) A2 (t , z ) S 2 ( ˆ , kˆ) A1 (t , z )
2
2
0
0
D d
D d
d
, k0 ) D1, 2 ( 0 , k0 ) i 1, 2
i 1, 2 ,
dt
dt
dt
d
S1, 2 ( ˆ , k0 ) S1, 2 ( 0 i , k0 ) S1, 2 ( 0 , k0 ).
dt
D1, 2 ( ˆ , k0 ) D1, 2 ( 0 i
~ (t ) B exp( i t )
A
1, 2
1, 2
1
~ (t )
dA
D
(
,
k
)
~
1
iS1 ( 0 , k0 ) 1 0 0 A2 (t ),
dt
1
~ (t )
dA
D
(
,
k
)
~ (t ).
2
iS 2 ( 0 , k 0 ) 2 0 0 A
1
dt
~ (t 0) A , A
~ (t 0) A
A
1
10
2
20
1
D D2
2
2 S1S 2 1
0
1
1 D
B2 S 2 2 B1
~
A1 (t ) a exp( i 0t ) b exp(i 0t )
~
A2 (t ) S 2 ( D2 ) 1 0 1 a exp( i 0t ) b exp(i 0t )
a
1
1
A10 0 S 2 1 ( D2 ) A20 , b A10 0 S 2 1 ( D2 ) A20
2
2

4.

2
2
Le
ku Lb2 Le2 Lb2 0
2
2
2
2
u Lb
Ab Lb
Sb ( ˆ , kˆ) Aw ,
t
z
Dw ( ˆ , kˆ) Aw w2 S w ( ˆ , kˆ) Ab .
2
2
2
u Lb
jb Lb
je ,
t
z
2
2
2
2 Le
je Le
jb .
t
Dw ( , k ) 0
0 k 0 u c
Db ( , k ) ( ku ) 0
2
2
Lb
2 Lb
2
2
0 , | | 0
1
D ( , k )
~ 2
S w ( 0 , k 0 ) S b ( 0 , k 0 ) w 0 0
Lb
2
w
2
Lb
~ 2 , m 1,2,3
| | Lb m m
Lb
13
| | Lb 1, 2
12
1 ~
i
Lb
2
~
dA
1
~ ,
b
i Lb Sb ( 0 , k0 ) A
w
dt
2
1
~
dA
D
(
,
k
)
~.
2
w
i w S w ( 0 , k0 ) w 0 0 A
b
dt
~
~
d 2 Ab
dAb
~
2
2
i
S
(
,
k
)
A
Lb
Lb
b
0
0
w,
2
dt
dt
1
~
dAw
Dw ( 0 , k0 ) ~
2
i w S w ( 0 , k0 )
Ab .
dt
2
2
Dw ( , k ) ku Lb
w2 Lb
S w ( , k ) S b ( , k ) 0
~ 1 A i (
~ S 1 1 ) A exp( t ) 1 A i (
~ S 1 1 ) A exp( t )
A
w
w0
b
0
b0
0
w0
b
0
b0
0
2
2
~
0 (1 2)
Lb

5.

B y
E x c B y
E
0,
c x 0
t 0 z
t
z
h 1
0 ( z ) h cos z
Ψ (t , z ) E x (t , z ), B y (t , z ) E x ( , k , z ), B y ( , k , z ) exp( i t ikz )
E x ( , k , z )
E ( , k ) exp(in z ),
n
n
E x ( , k , z ) E 1 exp( i z ) E0 E1 exp(i z ),
Bx ( , k , z ) B 1 exp( i z ) B0 B1 exp(i z ).
2
D 1 D0 D1 ( D 1 D1 ) 0
2
4
D0 ( , k ) 0
D 1 ( , k ) 0
1, 2
B y ( , k , z )
B ( , k ) exp(in z )
n
n
[ 2 (k ) 2 c02 ] E 1 2 ( 2) E0 0,
[ 2 k 2 c02 ] E0 2 ( 2) E 1 2 ( 2) E1 0,
[ 2 (k ) 2 c02 ] E1 2 ( 2) E0 0,
Dn 2 (k n ) 2 c02
1
1 2
2
kc0 1 1 2
4 2 4k
k2
k2
1
exp(
i
z
)
exp(
i
z
)
E x (t , z ) 2
2 ( 2k )
2 (2k )
exp( i t ikz ).
ψ (t , z )
Am
m
B
(
t
,
z
)
kc
k
(
k
)
k
(
k
)
y
m
1
1
exp( i z )
exp(i z )
m 2 (2k )
2 ( 2k )

6.

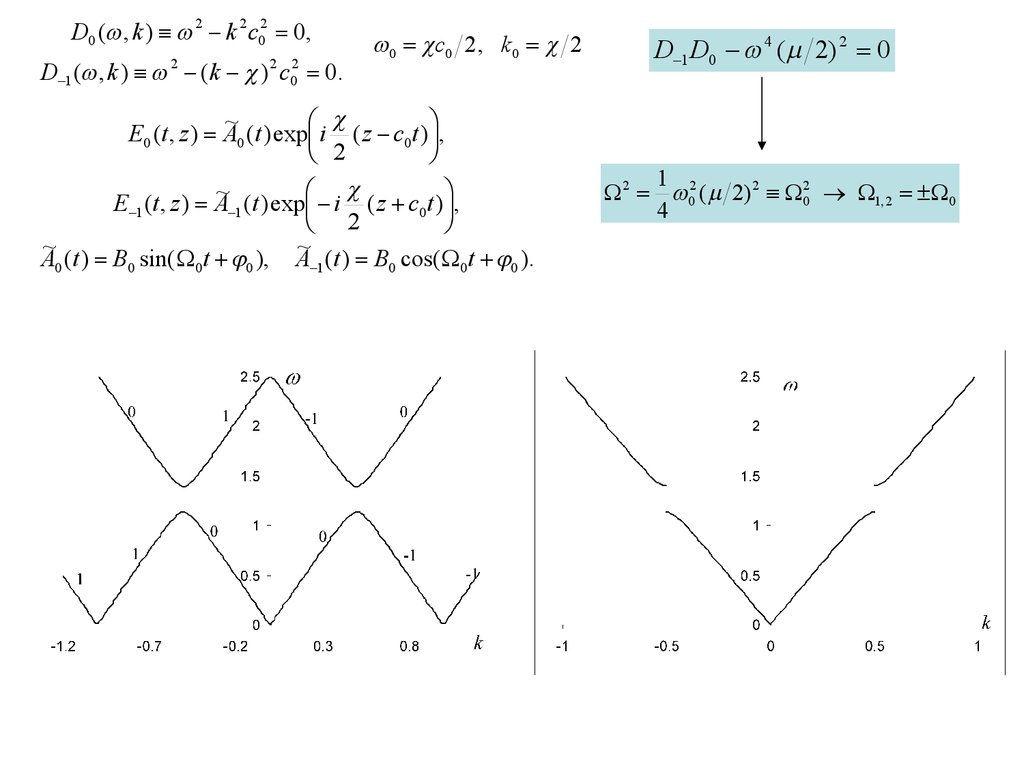
D0 ( , k ) 2 k 2 c02 0,
D 1 ( , k ) 2 (k ) 2 c02 0.
0 c0 2 , k 0 2
~
E0 (t , z ) A0 (t ) exp i ( z c0t ) ,
2
~ (t ) exp i ( z c t ) ,
E 1 (t , z ) A
1
0
2
~ (t ) B sin( t ), A
~ (t ) B cos( t ).
A
0
0
0
0
1
0
0
0
D 1 D0 4 ( 2) 2 0
1
2 02 ( 2) 2 02 1, 2 0
4

7.

( z)
D( ˆ , kˆ) A(t , z ) ( z )Q( ˆ ) A(t , z ) 0
A(t , z ) exp( i t ikz ) An exp(in z )
n
m
exp(im z )
m
D( , k n ) An Q ( ) m An m 0 , n 0, 1,
m
......................................................................
........ D 2 1 2 3 4 ......
........ 1 D 1
........ 2 1
........ 3 2
1 2 3 ......
D0
1 2 .......
1
D1 1......
........ 4 3 2
1 D2 ........
......................................................................
Dn D( , k n )
0
D0 D( , k )
Q( )
D 2 D 1 D0 D1 D2 2Q 2 ( ){| 1 |2 [ D0 ( D1 D2 D 1 D 2 ) D 2 D2 ( D 1 D1 )]
| 2 |2 [ D 2 D0 D2 D 1 D1 ( D 2 D2 )] | 3 |2 D0 ( D1 D 2 D 1 D2 ) | 4 |2 D 1 D0 D1} 0
D ( , k )
1 2 2 1Q( 0 ) 0 0 0
0
1
D0 D 1 0
D0 D 1 2Q 2 ( 0 ) | 1 |2 0
D 2 D 1 D0 D1 D2 2Q 2 ( ) | 1 |2 [ D0 ( D 1 D 2 D1 D2 ) D 2 D2 ( D 1 D1 )]
4Q 4 ( ) | 1 |4 ( D0 D 2 D2 ) 0
2
1
4 3
2 0
D ( , k )
2 2 2 | 2 |2 Q 2 ( 0 ) | D 1 ( 0 , k0 ) D1 ( 0 , k0 ) | 0 0 0
0
1

8.

k k 0 , | | k 0 2
D( 0 , k0 )
i B , B 1Q ( 0 )
k 0
1
A(t , z ) A ( z ) exp( i t ikz ) A ( z ) exp( i t ikz )
1
dA
dA
D
*
exp(ikz ) exp( ikz ) i Q( )
[ 1 exp(i z ) 1 exp( i z )][ A exp(ikz ) A exp( ikz )] 0.
dz
dz
k
1
D( 0 , k 0 )
dA
1 A 0 ,
i Q ( 0 )
dz
k
0
1
D( 0 , k 0 ) *
dA
1 A 0 .
i Q( 0 )
dz
k 0
A ( z ) B exp( B z ) C exp( B z ) ,
A ( z ) [ B exp( B z ) C exp( B z )] ,
A(t , z ) C exp( B z ) exp( i 0t ik 0 z ) C exp( B z ) exp( i 0t ik 0 z )