Similar presentations:
Математические методы прогноза и восстановления зависимостей
1.
Математические методыпрогноза и восстановления
зависимостей
2.
Аппроксимация – замена одних объектов(функций) другими
Интерполяция – способ нахождения
промежуточных значений величины по
имеющемуся дискретному набору
известных ее значений
Вид аппроксимирующей функции ?
Число и положение точек, в которых
известно значение функции (узловых точек) ?
3.
Полиномиальная аппроксимация2
n
y
a
a
x
a
x
...
a
x
0 1 2
n
Степень полинома на единицу меньше числа
узловых точек
2
n
y
a
a
x
a
x
...
a
x
1
0
1
1
2
1
n
1
2
n
y
a
a
x
a
x
...
a
x
2 0 1
2 2
2
n
2
......................
2
n
y
a
a
x
a
x
...
a
x
n 0 1
n 2
n
n
n
4.
Кусочно полиномиальная аппроксимацияПолиномы Лагранжа
n 1
(x xi)
n 1
i 1(i j)
y
yj n 1
j 1
(
x
x
)
j
i
i 1(i j)
(
x
x
)(
x
x
)(
x
x
)(
x
x
)(
x
x
)(
x
x
)
2
3
1
3
1
2
y
y
y
y
1
2
3
(
x
x
)(
x
x
)
(
x
x
)(
x
x
)
(
x
x
)(
x
x
)
1
2
1
3
2
1
2
3
3
1
3
2
5.
Многочлены Эрмитаn
1
y
H
(
x
)
y
h
(
x
)
y
j
j
j
j
j
1
n
1
(x xj)
(x xi)2
hj
i
1(i j)
n
1
2
(
x
x
)
j i
i
1(i j)
n
1
1
a
2
x
i
1x
j
i
n
1
(ax
b)
(x xi)2
Hj
i
1(i j)
n
1
2
(
x
x
)
j i
i
1(i j)
b 1 axj
6.
Полиномы Ньютонаy
y
(
x
x
)[
x
,
x
]
(
x
x
)(
x
x
)[
x
,
x
,
x
]
.
0
0
1
0
0
1
2
1
0
(
x
x
)(
x
x
)...(
x
x
)[
x
,...
x
]
0
1
n
1
n
n
yj y
i
[xj,x
i]
xj x
i
[
x
,
x
]
[
x
,
x
]
i
1
i
i
i
1
[
x
,
x
,
x
]
i
1
i
i
1
x
x
i
1
i
1
7.
Многочлены Чебышеваy
b
b
T
b
T
...
b
T
0
1
1
2
2
m
m
T0 1
T1 x
T
2
xT
T
n
1
n
n
1
Аппроксимация рациональными функциями
N(x)
y
D(x)
8.
Сплайн-интерполяцияКвадратичный сплайн
2
y
a
b
(
x
x
)
c
(
x
x
)
i
i
i
1
i
i
1
xi 1 x xi
ai yi 1
2
y
a
b
(
x
x
)
c
(
x
x
)
i
i
i
i
i
1
i
i
i
1
y
(
x
0
)
y
(
x
0
)
i
i
y (x0) 0
9.
Кубический сплайн2
3
y
a
b
(
x
x
)
c
(
x
x
)
d
(
x
x
)
i
i
i
1
i
i
1
i
i
1
xi 1 x xi
ai yi 1
2
3
y
a
b
(
x
x
)
c
(
x
x
)
d
(
x
x
)
i i ii i
1ii i
1 ii i
1
y
(
x
0
)
y
(
x
0
)
i
1
i
1
y
(
x
0
)
y
(
x
0
)
i
i
"
(
x
0
)
y
"
(
x
0
)
y
''(
x
0
)
y
"
(
x
0
) y
i
i
i
1
i
1
(
(
y
x
)
y
x
)
0
0
n
10.
ai yi 1(1)
a
b
h
c
h
d
h
y
i
i
i
i
i
(2)
b
2
c
h
3
d
h
b
0
i
i
i
i
1
(3)
c
3
d
c
0
i
ih
i
1
(4)
2
3
2
c
1 c
n
1 0
11.
Метод прогонкиA
c
D
c
B
c
G
ii
1
ii
ii
1
i
c
c
i
i
1
i
1
i
1
B
i
i
1
D
A
i
i
i
G
A
i
i
i
i
1
D
A
i
i
i
12.
Интерполяция с использованиембазисного сплайна
n
yi siBi
i 1
1
3
B
(
x
x
)
i
i
2
3
4
h
xi 2 x xi 1
xi 1 x xi
1
3
3 23 3
B
(
x
x
)
(
x
x
)
(
x
x
)
i
i
1
i
1
i
1
2
3
4
4
h 4
h
4
h
xi x xi 1
1
3
3 23 3
B
(
x
x
)
(
x
x
)
(
x
x
)
i
i
1
i
1
i
1
2
3
4
4
h 4
h
4
h
xi 1 x xi 2
1
3
B
(
x
x
)
i
2
3 i
4
h
13.
Аппроксимация Фурьеn
1
n
1
y
a
/
2
a
cos(
kx
/
n
)
b
sin(
kx
/
n
)
a
/
2
c
x
)
0
k
k
n
k
1
N 2n
2
n
1
k
1
h 1
2
n
1
a
1
/
n
y
(
x
)
cos(
kx
/
n
) b
1
/
ny
(
x
)
sin(
kx
/
n
)
k
k
x
0
x
0
14.
πkna k = ( cos )U 2n− 1 − U 2n− 2 +f (0 )
n
πk
nb k = (sin )U 2n− 1
n
U0 0
U 1 =f (2n− 1 )
πk
U m = (2cos )U m− 1 − U m− 2 +f (2n − m)
n
15.
Использование усеченного ряда (M гармоник)∑ ( f − f M )2 = ∑
x
x
[
2
M
a
0
2
f −n
+ ∑ ( a2k +b2k )
2 k=1
Ряд по косинусам
N
1
x
N
1
N−1
k
f
(− 1 )
2 0
πk
ak =
+ ∑ f ( x ) cos
x+
fN
N 2 x=1
N
2
[
]
]
16.
Медленное изменение по времениN
1
x N
N
a
(
t
)
1
/
N
y
(
x
t
)
cos(
mx
/
N
)
m
x
N
1
N
b
(
t
)
1
/
N
y
(
x
t
)
sin(
mx
/
N
)
m
x
N
1
17.
Смешение частотA
a
2
a
0
0
2
jN
j
1
A
a
(
a
a
)
k
k
2
(
j
k
)
N
2
(
j
k
)
N
j
1
B
b
(
b
b
)
k
k
2
(
j
k
)
N
2
(
j
k
)
N
j
1
18.
Сигма-множители Ланцоша.• Прямоугольная волна с периодом
2
N
1
y
1
/
2
2
/
sin((
2
k
1
)
x
)
2
k
1
k
1
x
/
2
N
N
N
1
2
1
sin[
2
k
1
)
/
2
N
]
y
y
(
)
d
si
2
k
1
)
x
)
2
2
k
1
(
2
k
1
)
/
2
N
k
1
x
/
2
N
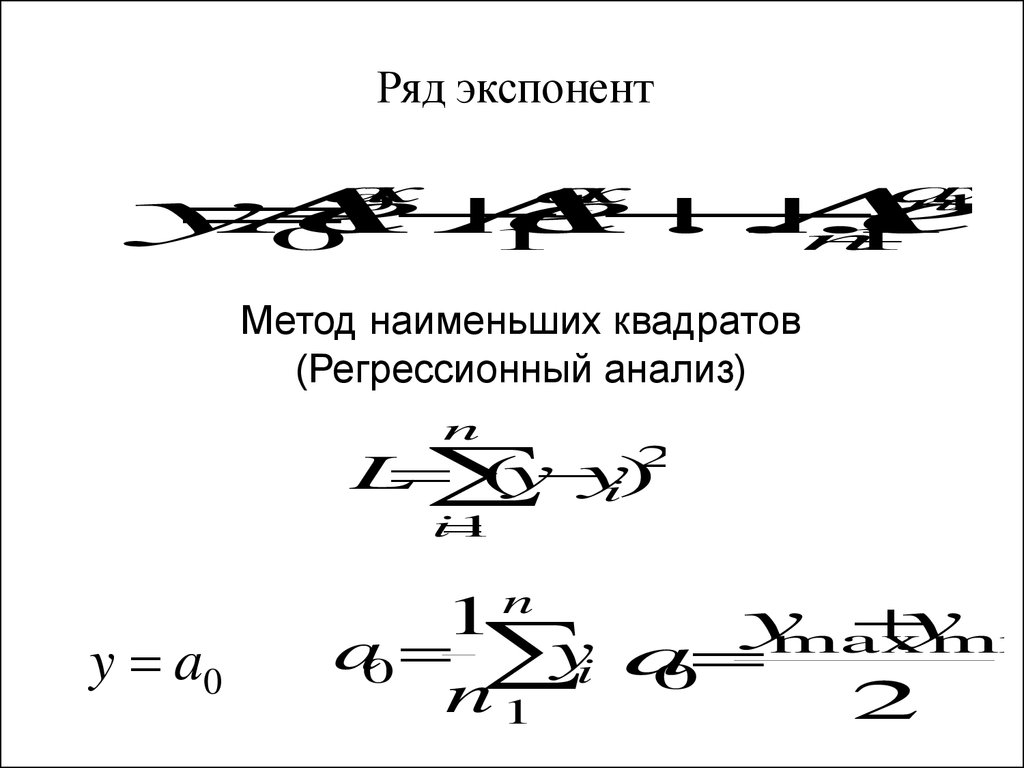
19.
Ряд экспонентy
A
e
A
e
...
A
e
a
x
0
0
a
x
1
1
a
x
n
1
n
1
Метод наименьших квадратов
(Регрессионный анализ)
n
2
L
(
y
y
)
i
i
1
1
y
y
max
min
a0
yi a
0
n1
2
n
y a0
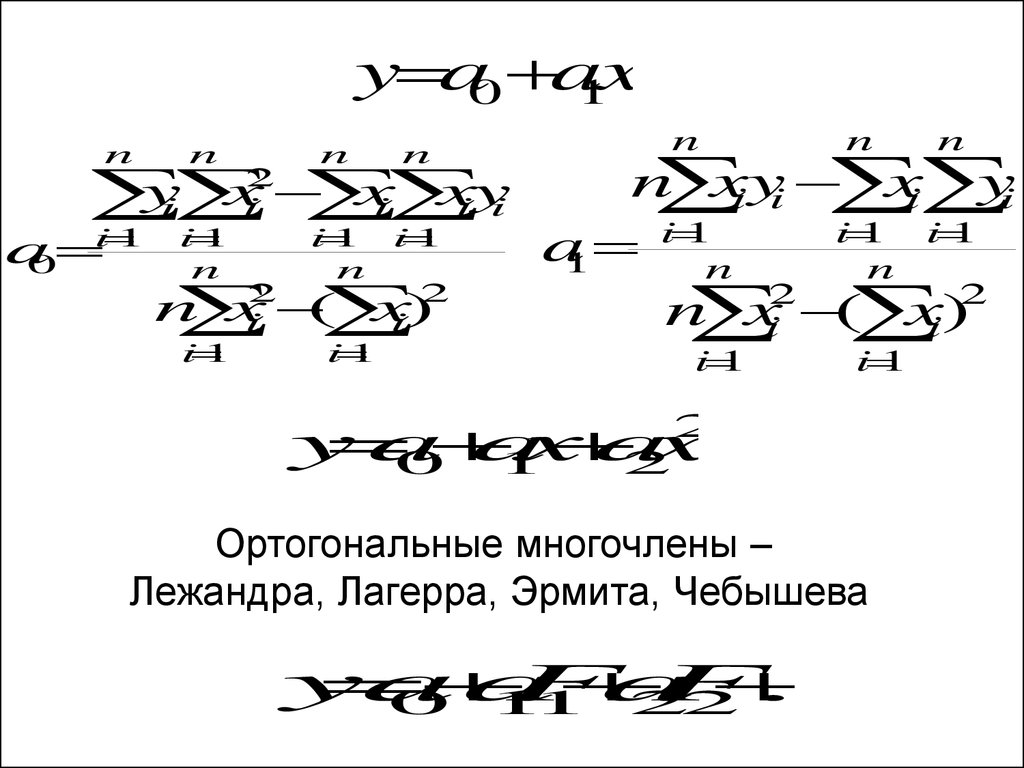
20.
y a0 a1xn
n
n
n
2
yi x
x
i x
i
iy
i
i
1 i
1
i
1 i
1
a
0
n
n
2
2
n x
(
x
)
i
i
i
1
i
1
n
n
n
n
xiyi
xi yi
i
1 i
1
a1 i 1n
n
2
2
n
xi (
xi)
i
1
i
1
y
a
a
x
a
x
0
1
2
2
Ортогональные многочлены –
Лежандра, Лагерра, Эрмита, Чебышева
y
a
a
F
a
F
...
0
1
1
2
2
21.
Полиномы ЛежандраP0 1
P1 x
1 2
P
3
x
1
)
2 (
2
1 4
2
P
(
35
x
30
x
3
)
4
8
1 3
P
5
x
3
x
)
3 (
2
y
a
a
(x
x
)
1
'
0
22.
Оценка дисперсии2
V(a )
'
0
SS
2
ош
n 2
2
V(a1 )
Sxx
n
SS
(
y
y
ˆj)
ош
j
2
j
S
(x
x
)
xx
j
2
j
Множественный коэффициент детерминации
ˆ y)
(y
2
R
2
j
j
(y y)
2
j
j
23.
Многомерная регрессия2
2
y
x
x
...
x
x
...
x
x
.
i 0
1
i
1
i 2
i
2
i
11
i
1
i 22
i
2
i
12
i
1
i
2
i
2
2
L
(
y
x
)
(
)
i
0
jij
0
j
i
yt
xit
j
j
yt
( ixit)
i
i
y
(
x
fi)
t
it
i
z
i
j
i
j
y
x
(
y
x
)
t
it
t
1
i
,
t
1
i
i
24.
Множество исходных данных разбивается натри множества: обучающее, проверочное и контрольное
2
2
y
a
a
x
a
x
a
x
x
a
x
a
x
j
0
j
1
j
j 2
j
3
j
j
4
jj
j 5
2
2
z
a
a
y
a
y
a
y
y
a
y
y
y
l
0
l
1
l
l 2
l
3
l
l 4
ll
l
5
2
y
(
a
a
x
a
x
)
0
i
1
i i
2
i i
i
25.
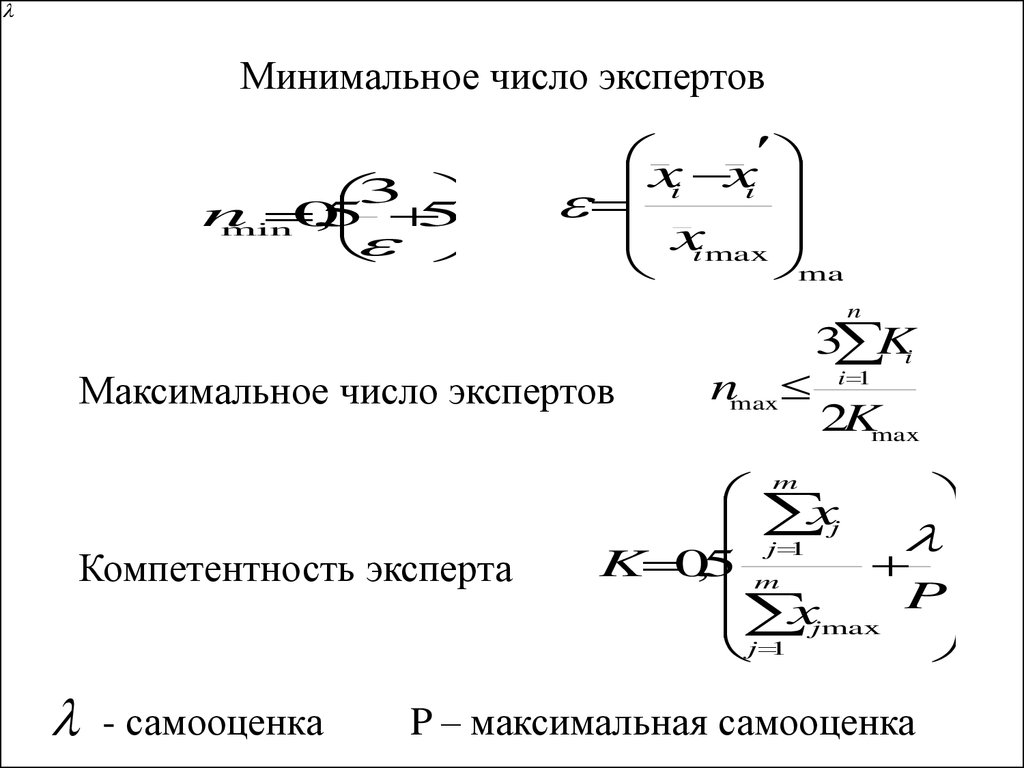
Минимальное число экспертов3
n
0
,5
5
min
x x
i
i
ximax
max
n
Максимальное число экспертов
nmax
3 Ki
i 1
2Kmax
x
j
j 1
K 0,5 m
x
P
jmax
j 1
m
Компетентность эксперта
- самооценка
P – максимальная самооценка
26.
ln
x
q
x
i
kK
Среднее взвешенное
k
1j
1
Вес
Wij
n
xij
m
Wi
x
i 1
k
j ij
ij
Вариационный размах
W
ij
j 1
n
R
x
x
i
imax imin
x x
2
n
Среднеквадратичное отклонение
Коэффициент вариации
V
i
xi
j 1
ij
i
n 1
27.
Коэффициент ранговой корреляции Спирменаxij xif
6
1 i 1 2
m 1
m
m
2
Коэффициент конкордации
2
1
12
x
m
1
ij n
i
1
j
1
2
W
K
2
2
m
n
m
1
m
n
28.
Скользящее среднееi t p
1) сглаживание
yt
di
i t p
2 p 1
i t p
сглаживание с весом y t
i t p
fi 1
i t p
d i fi
i t p
i t p
fi
i t p
29.
2) прогноз1 i t
y
d
i
1
i
p
1
i
t
p
1
y
y
d
d
)
t
1
t (
t
t
p
p
1
Экспоненциально взвешенное среднее
2
3
y
d
(
1
)
d
(
1
)
d
(
1
)
d
.
t
1
t
t
1
t
2
t
2
y
d
(
1
)
y
t
1
t
t
1
30.
Прогноз при наличии трендаАддитивный тренд
Метод Холта
yt u
b
t
t
u
Ad
(
1
A
)(
u
b
)
t
t
t
1
t
1
b
B
(
u
u
)
(
1
B
)
b
t
t
t
1
t
1
31.
Модификация Муираy
u
b
[
(
1
A
)
/
A
]
t
t
t
u
Ad
(
1
A
)
u
t
t
t
1
b
B
(
u
u
)
(
1
B
)
b
t
t
t
1
t
1
Метод Бокса-Дженнингса
yt 1 ut
t
u
u
(
e
e
)
e
e
t
t
1
1
t
t
1
0
t
1
t
et dt yt
t
32.
Двойное сглаживание Браунаyt ft b
t
ft 2ut ut
b
(
u
u
t
t
t)
1
u
d
(
1
)(
u
b
)
t
t
t
1
t
1
u
u
(
1
)
u
t
t
t
1
33.
Адаптивное сглаживание Браунаyt ft b
t
2
u
u
b
(
1
)
e
t
t
1
t
1
t
2
b
b
(
1
)e
t
t
1
t
et dt yt
Мультипликативный тренд
yt trt
Метод Муира
d
(
1
)
r
t
t
t
t
1
d
t
r
(
1
)
r
t
t
1
t
1
34.
Сезонномультипликативный трендМетод Холта - Винтера
f
(
u
b
)
F
t
t
t
t
L
d
t
u
A
(
1
A
)(
u
b
)
t
t
1
t
1
F
t
b
B
(
u
u
)
(
1
B
)
b
t
t
t
1
t
1
d
t
F
C
(
1
C
)
F
t
t
L
u
t
1n
Fk 1
nk 1
35.
fu
1
b
t
t(
t)F
t
L
Ad
t
u
(
1
A
)(
1
b
)
u
t
t
1
t
1
F
t
L
B
(
u
u
)
t
t
1
b
(
1
B
)
b
t
t
1
u
t
1
Cd
t
F
(
1
C
)
F
t
t
L
u
t
36.
Сглаживание ряда (скользящее среднееили медианное) по периоду
Выделение тренда и определение
коэффициентов сезонности
аддитивных или мультипликативных
Нормирование коэффициентов сезонности
37.
Фиктивные переменныеn
y
a
a
t c
D
t
0
1
i i
i
1
1
событ
_
прои
D
i
0
событи
_
не
_
прои
38.
Метод Кростона(предсказание редких событий)
u
Ad
(
1
A
)
u
t
t
t
1
L
B
(
1
B
)
L
t
t
t
1
Вероятность того, что суммарные
продажи за n шагов на превысят z
z
n
m
m
n
mm
n
m
1
0
n
F
(
z
)
q
C
p
q
f(
x
)
dx
39.
Метод задержекxp xp 1
xN
x
xp 1 xp 2
N 1
x
x
x
N
p
1
1 2
p
p
p
i
1
j
1
k
j
x
a
a
x
b
x
x
N
1
0
i
N
p
1
jk
N
p
j
N
p
k
40.
Адаптивные методыМетод Чоу
y
d
(
1
)
y
t
1
t
t
1
уточняется после каждого шага (выбором из
трех близких значений)
Метод Тамара
yt u
b
t
t
u
Ad
(
1
A
)(
u
b
)
t
t
t
1
t
1
b
B
(
u
u
)
(
1
B
)
b
t
t
t
1
t
1
A 0,02
41.
Метод Тригга и Лича~
~
f
u
T
d
(
1
T
)
u
t
t tt
t t
1
et
Tt
MAD
t
e
e
(
1
)
e
t
t
t
1
et dt yt
MAD
e
(
1
)
MAD
t
t
1
42.
Автокорреляционный анализn
(dt d)(
dt k d)
t k
1
rk
1 n
2
(dt d)
n 1t 1
n
1
d
dt
nt 1
u
r
d
et
t
1
1
t
Метод кумулятивных сумм
k
Qk et
t 1
a
L
(
t
n
b
)
1
,2
b
L
Q
u
u
u
1
,
2
t
t









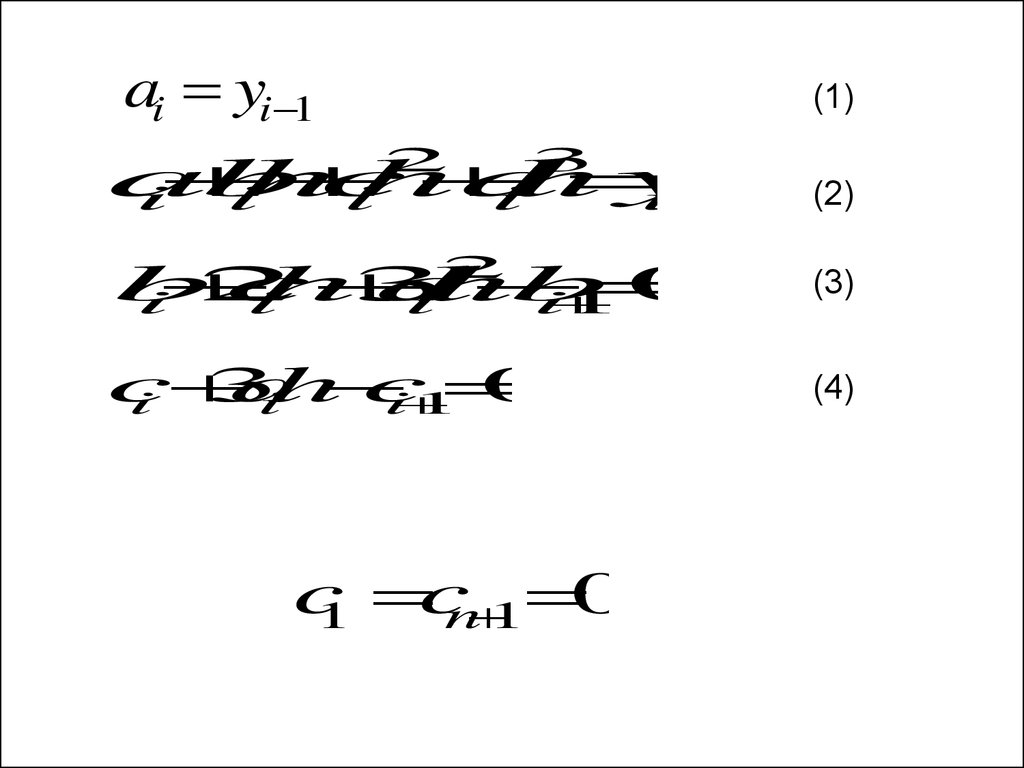



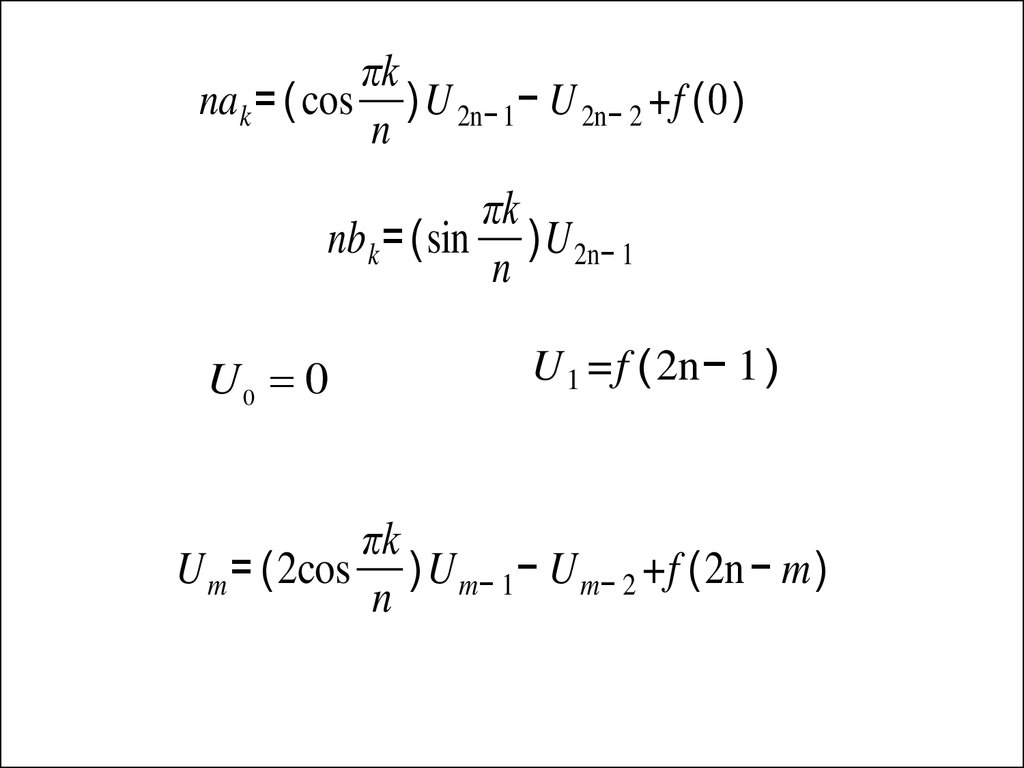

























 mathematics
mathematics








