Similar presentations:
Метод Эверхарта
1.
АВДЮШЕВ Виктор АнатольевичНЕИЗВЕСТНЫЙ
МЕТОД ЭВЕРХАРТА
1
2.
«КРЫЛАТЫЕ ФРАЗЫ»НЕЗНАНИЕ
ПОЧИТАНИЕ
НЕПРИЯЗНЬ
Методы Рунге–Кутты —
вчерашний день. Иное
дело — метод Эверхарта!
Кто использует метод
Эверхарта — просто пижон!
Современные методы
Рунге–Кутты рулят!
2
3.
“I have the impression thatthe proposed method is equivalent to
an implicit Runge-Kutta method.”
E. Hairer about Everhart’s Method
3
4.
ОРБИТАЛЬНОЕДВИЖЕНИЕ S
E
x
A
J
ЗАДАЧА КОШИ
ИМЕЕМ
НАЙТИ
dx
f (t , x), x 0 x(t0 )
dt
x(t0 t )
4
5.
МЕТОДЫ РУНГЕ–КУТТЫx1 x 0 h j 1 b j f j ,
s
fi f (t0 hci , x 0 h j 1 aij f j ) (i 1,
s
К. Рунге
, s)
М. Кутта
5
6.
МЕТОДЫ РУНГЕ–КУТТЫx1 x 0 h j 1 b j f j ,
s
fi f (t0 hci , x 0 h j 1 aij f j ) (i 1,
s
, s)
УСЛОВИЯ ПОРЯДКА
x1 Φ(h, t0 , x0 )
Φ( i ) (0, t0 , x0 ) i
x1 x0
h
i!
i 1
f ( i 1) (t0 , x 0 ) i
x(t1 ) x 0
h
i!
i 1
6
7.
КОЛЛОКАЦИОННЫЕ МЕТОДЫКОЛЛОКАЦИОННЫЙ МНОГОЧЛЕН
x1 Φ(h, t0 , x0 ) g(t0 h), g(t0 ) x0 ,
g (t0 hci ) f (t0 hci , g(t0 hci )) (i 1,
, s)
ИНТЕРПОЛЯЦИЯ ЛАГРАНЖА
g (t0 h ) j 1 f j l j ( ), l j ( ) m j
s
cm
c j cm
ПРИБЛИЖЕННОЕ РЕШЕНИЕ
x1 x0 h j 1 f j l j ( ) d ,
s
1
0
fi f (t0 hci , x 0 h j 1 f j l j ( ) d ) (i 1,
s
ci
0
, s)
7
8.
КОЛЛОКАЦИОННЫЕ МЕТОДЫg (t0 h ) i 1 f (t0 hci , g (t0 hci ))li ( )
s
x (t0 h ) i 1 f (t0 hci , x(t0 hci ))li ( ) O (h s )
s
x(t0 h ) g (t0 h ) h i 1[f (t0 hci , x(t0 hci ))
s
f (t0 hci , g (t0 hci ))] li ( ) d O(h s 1 )
0
B max i 1 li ( ) d
s
[0,1]
0
M max || x(t0 h ) g(t0 h ) ||
[0,1]
M hLBM O (h s 1 ) M O (h s 1 )
p s
8
9.
МЕТОДЫ ГАУССАВОЗМУЩЕННОЕ УРАВНЕНИЕ
g f (t , g) p(t )
ЛИНЕАРИЗАЦИЯ
f
g x
(g x) p(t ) O(h 2 s 2 )
x x x ( t )
МЕТОД ВАРИАЦИИ ПОСТОЯННЫХ
1
x1 x(t0 h) h Φ(t0 h)Φ 1 (t0 h )[p(t0 h ) O(h 2 s 2 )]d
0
КВАДРАТУРА ГАУССА
1
0
Φ(t0 h)Φ 1 (t0 h )p(t0 h ) d
i 1 bi Φ(t0 h)Φ 1 (t0 hci ) p(t0 hci ) O (h 2 s )
s
0
9
10.
Дж. БутчерМЕТОДЫ ГАУССА
РАЗБИЕНИЕ ЛЕЖАНДРА
c1 ,
s
, cs
p 2s
d
s
s
[
(
1)
] 0
s
dt
РАЗБИЕНИЕ РАДО
РАЗБИЕНИЕ ЛОБАТТО
p 2s 1
p 2s 2
d s 1 s
s 1
[
(
1)
] 0
s 1
dt
d s 2 s 1
s 1
[
(
1)
] 0
s 2
dt
10
11.
КОЛЛОКАЦИОННЫЕ МЕТОДЫКОЛЛОКАЦИОННЫЙ МНОГОЧЛЕН
x1 Φ(h, t0 , x0 ) g(t0 h), g(t0 ) x0 ,
g (t0 hci ) f (t0 hci , g(t0 hci )) (i 1,
, s)
ИНТЕРПОЛЯЦИЯ ЛАГРАНЖА
g (t0 h ) j 1 f j l j ( ), l j ( ) m j
s
cm
c j cm
ПРИБЛИЖЕННОЕ РЕШЕНИЕ
x1 x0 h j 1 f j l j ( ) d ,
s
1
0
fi f (t0 hci , x 0 h j 1 f j l j ( ) d ) (i 1,
s
ci
0
, s)
11
12.
МЕТОД ЭВЕРХАРТАКОЛЛОКАЦИОННЫЙ МНОГОЧЛЕН
x1 Φ(h, t0 , x0 ) g(t0 h), g(t0 ) x0 ,
g (t0 hci ) f (t0 hci , g(t0 hci )) (i 1,
, s)
КАНОНИЧЕСКАЯ ИНТЕРПОЛЯЦИЯ
g (t0 h ) j 1 a j j 1
s
ПРИБЛИЖЕННОЕ РЕШЕНИЕ
x1 x 0 h j 1
s
Э. Эверхарт
aj
j
12
13.
МЕТОД ЭВЕРХАРТАВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ
j 1
a
c
j 1 j i fi f (t0 hci , y i )
s
C {cij 1}
B C 1 {bij }
j 1 f j bij ai , y i x0 h j 1
s
s
aj
j
cij
ИТЕРАЦИИ
f a x
a y
13
14.
МЕТОД ЭВЕРХАРТАНЬЮТОНОВСКАЯ ИНТЕРПОЛЯЦИЯ
g (t0 h ) j 1 α j i 1 ( ci )
j 1
s
СВЯЗЬ МЕЖДУ ПОЛИНОМАМИ
ai j i c ji α j
s
αi j i d ji a j
s
ИТЕРАЦИИ
f α
a y a x
14
15.
МЕТОД ЭВЕРХАРТАНЬЮТОНОВСКАЯ ИНТЕРПОЛЯЦИЯ
g (t0 h ) j 1 α j i 1 ( ci )
j 1
s
ПРИБЛИЖЕННОЕ РЕШЕНИЕ
x1 x0 h j 1 α j
s
1
0
I ( x, k )
x
0
k
i 1
j 1
i 1
( ci )d
( x xi )d x
ИТЕРАЦИИ
f α x
α y
15
16.
МЕТОД ЭВЕРХАРТАИНТЕРПОЛЯЦИЯ ЛАГРАНЖА
g (t0 h ) j 1 f j l j ( )
s
ПРИБЛИЖЕННОЕ РЕШЕНИЕ
x1 x0 h j 1 f j l j ( )d
1
s
0
I ( x, k )
x
0
k
i 1
( x xi )d x
ИТЕРАЦИИ
f y f x
16
17.
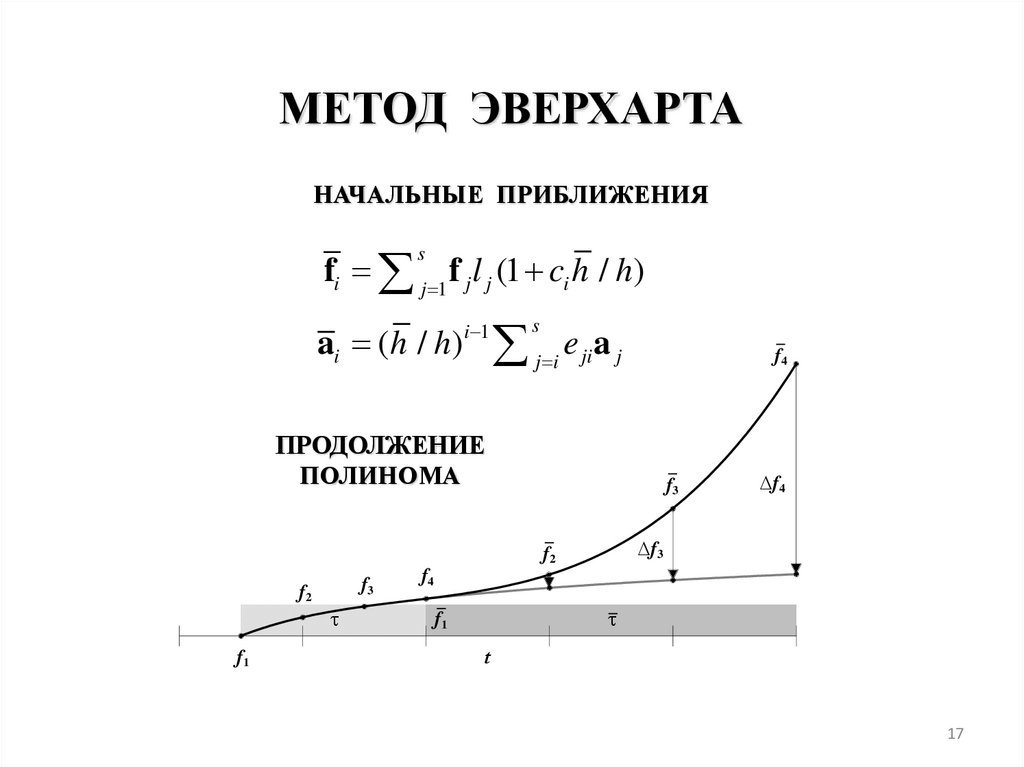
МЕТОД ЭВЕРХАРТАНАЧАЛЬНЫЕ ПРИБЛИЖЕНИЯ
fi j 1 f j l j (1 ci h / h)
s
ai (h / h)
i 1
s
j i
e ji a j ai
ПРОДОЛЖЕНИЕ
ПОЛИНОМА
f3
f3
f1
f4
f3
f2
f2
f4
f4
f1
t
17
18.
1. НЕЯВНЫЙ РУНГЕ-КУТТЫ2. КОЛЛОКАЦИОННЫЙ
3. ГАУССА
18
19.
1. НЕЯВНЫЙ РУНГЕ-КУТТЫ2. КОЛЛОКАЦИОННЫЙ
3. ГАУССА
4. ЛЮБОЙ ПОРЯДОК
19
20.
1. НЕЯВНЫЙ РУНГЕ-КУТТЫ2. КОЛЛОКАЦИОННЫЙ
3. ГАУССА
4. ЛЮБОЙ ПОРЯДОК
5. РЕШЕНИЕ КАК ПОЛИНОМ
20
21.
1. НЕЯВНЫЙ РУНГЕ-КУТТЫ2. КОЛЛОКАЦИОННЫЙ
3. ГАУССА
4. ЛЮБОЙ ПОРЯДОК
5. РЕШЕНИЕ КАК ПОЛИНОМ
6. ОРБИТАЛЬНО УСТОЙЧИВ
7. ГЕОМЕТРИЧЕСКИЙ
21
22.
1. НЕЯВНЫЙ РУНГЕ-КУТТЫ2. КОЛЛОКАЦИОННЫЙ
3. ГАУССА
4. ЛЮБОЙ ПОРЯДОК
5. РЕШЕНИЕ КАК ПОЛИНОМ
6. ОРБИТАЛЬНО УСТОЙЧИВ
7. ГЕОМЕТРИЧЕСКИЙ
8. КОНТРОЛЬ ШАГА
||e||cal
22
23.
ОЦЕНКА ТОЧНОСТИПРИБЛИЖЕННОЕ РЕШЕНИЕ
x1 x 0 h j 1
s
aj
j
|| a s ||
|| α s ||
|| e ||cal h
h
s
s
ВЫБОР ШАГА
|| e ||tol
h h
||
e
||
cal
1
s
ПРОБЛЕМА
2 s 2 (Lobatto)
p 2 s 1 (Radau)
h
2s
(Legandre)
for
p s 1
23
24.
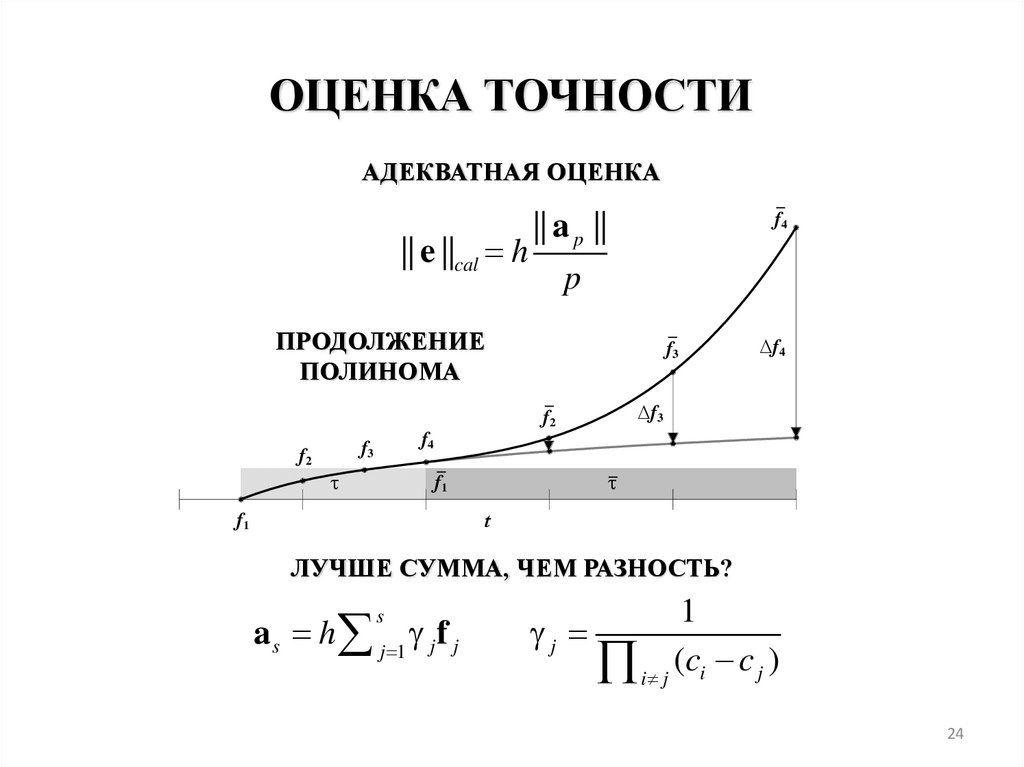
ОЦЕНКА ТОЧНОСТИАДЕКВАТНАЯ ОЦЕНКА
|| e ||cal h
f4
|| a p ||
p
ПРОДОЛЖЕНИЕ
ПОЛИНОМА
f3
f3
f2
f4
f3
f2
f4
f1
t
f1
ЛУЧШЕ СУММА, ЧЕМ РАЗНОСТЬ?
a s h j 1 j f j
s
1
j
i j (ci c j )
24
25.
2526.
2627.
2728.
СПАСИБО ЗА ВНИМАНИЕ!28




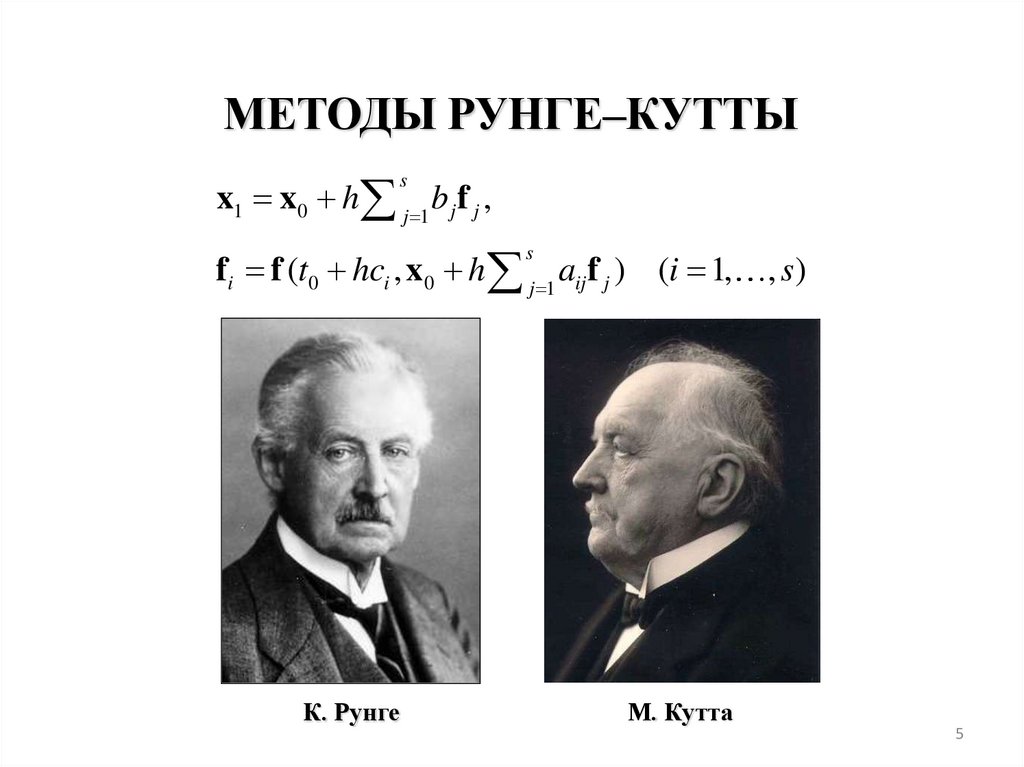





















 mathematics
mathematics








