Обзор численных методов

1.

РХТУ им. Д.И. Менделеева
Каф. ИКТ
Курс создал: ст. преп. A.М. Васецкий
1

2. Литература

В. М. Вержбицкий, Основы численных
методов, Высшая школа, 2005 г.
А.А. Амосов, Ю.А. Дубинский, Н.В.
Копченова, Вычислительные методы
для инженеров, Высшая школа, 1994
А. В. Пантелеев, Т. А. Летова Методы
оптимизации в примерах и задачах.
Прикладная математика для ВТУЗов,
Высшая школа, 2008
2

3. Решение нелинейных алгебраических уравнений

Пусть функция f(x) определена
и непрерывна при всех х на
отрезке [а,b] и на [а,b] меняет
знак, т.е. f(a)*f(b)<0.
Тогда уравнение f(x)=0 имеет
на (а, b) хотя бы один корень.
3

4. Решение нелинейных алгебраических уравнений. Алгоритм метода половинного деления

В. М. Вержбицкий, Основы численных методов, Высшая
школа, 2005 г.
4

5. Блок-схема метода половинного деления

5

6. Решение нелинейных алгебраических уравнений. Алгоритм метода секущих

Х0 и Х1 – начальные точки. Задаются
пользователем.
Метод не сходится при Хk=Xk-1
Примечание: Решение уравнений, где Х –
кратный 0 (f’(x)=0) представляет для
метода определённые трудности.
В. М. Вержбицкий, Основы численных методов, Высшая
школа, 2005 г.
6

7. Решение нелинейных алгебраических уравнений. Алгоритм метода Стеффенсена

Х0– начальная точка.
Метод не сходится при Хk=Xk-1
Решение уравнений, где Х – кратный 0
(f’(x)=0) представляет для метода
определённые трудности.
Локально имеет квадратичную
сходимость
В. М. Вержбицкий, Основы численных методов, Высшая
школа, 2005 г, с.221
7

8. Решение нелинейных алгебраических уравнений. Алгоритм метода простой итерации

Чтобы применить метод простой
итерации необходимо
преобразовать исходное уравнение
к виду х= (x).
Далее выбирается начальное
приближение корня х0 и
вычисления проводят по схеме
xn+1= (xn).
Сходимость обеспечивается при
| ’(xn)|<q<1
8

9. Трёхдиагональная СЛАУ

Трёхдиагональными называются
матрицы, каждая строка которых
содержит 3 соседних неизвестных:
bixi-1+cixi+dixi+1=ri, b1=0, dn=0, i=1..n
Или в матричной форме:
9

10. Системы линейных алгебраических уравнений (СЛАУ)

СЛАУ в матричном виде
записывается как А*x=b, где
В Excel удобно решать СЛАУ с
использованием функций листа
Excel и формулы:
x=A-1b
10

11. Решение трёхдиагональной СЛАУ методом прогонки

Прямой ход метода прогонки:
Определение коэффициентов di, li, i=2..n
d1=-d1/c1; l1=r1/c1
Обратный ход метода прогонки:
xn=ln
xi=dixi+1+li i=n-1,..1
Задача корректна (ci+bidi-1≠0) и устойчива
(|di|<1) при
|ci|>|bi|+|di|
11
В. М. Вержбицкий, Основы численных методов, Высшая школа, 2005 г, с.75

12. Решение СЛАУ методом Гаусса

Прямой ход метода Гаусса
(приведение к треугольному виду)
Обратный ход метода Гаусса
(получение значений неизвестных)
12

13. Алгоритм решения СЛАУ методом Гаусса

В. М. Вержбицкий, Основы численных методов, Высшая школа, 2005 г
13

14. LU-разложение

Любая матрица А(n x n) может быть
преобразована представлена как
произведение нижней (L) и верхней (U)
треугольных матриц следующим образом:
Элементы uij и lij находятся поочерёдно.
Из 1-й строки: u1j=a1j (j=1…n)
Из оставшейся части 1-го столбца:
li1=ai1/u11 (i=2…n)
14

15. LU-разложение (продолжение)

Из оставшейся части 2-й строки
u2j=a2j-l21u1j (j=2,...,n)
Из оставшейся части 2-го столбца
li2=(ai2-li1u12)/u22 (i=3,…,n)
…
Т.е. все отличные от 0 и 1
элементы матриц L и U могут быть
вычислены при помощи формул:
15

16. Решение СЛАУ при помощи LU-разложения

Система Ax=b преобразуется к
LUx=b
Или, вводя вектор
вспомогательных переменных y:
Ly=b и Ux=y
i=1..n
i=n..1
16

17. Решение СЛАУ методом простых итераций

Сначала надо привести функцию,
удобному для метода итераций: x= (x).
Итерационная процедура представлена в
виде:
Сходимость метода обеспечивается в
случае, когда норма матрицы Якоби меньше
либо равна константе q:
|| ‘||≤q<1
А.А. Амосов, Ю.А. Дубинский, Н.В. Копченова, Вычислительные методы
для инженеров, Высшая школа, 1994
17

18. Решение СЛАУ методом Зейделя

Вариант метода простых итераций,
где часть переменных хk заменена на
xk+1
В. М. Вержбицкий, Основы численных методов, Высшая школа, 2005 г
18

19. Одномерная оптимизация. Метод деления отрезка пополам

19

20. Одномерная оптимизация. Метод деления отрезка пополам

А. В. Пантелеев, Т. А. Летова. Методы оптимизации в примерах и
задачах. Прикладная математика для ВТУЗов, Высшая школа, 2008
20

21. Одномерная оптимизация. Метод золотого сечения

А. В. Пантелеев, Т. А. Летова Методы оптимизации в примерах и
задачах. Прикладная математика для ВТУЗов, Высшая школа, 2008
21

22. Одномерная оптимизация. Метод Фибоначчи

22

23. Одномерная оптимизация. Метод Фибоначчи (продолжение)

А. В. Пантелеев, Т. А. Летова Методы оптимизации в примерах и
задачах. Прикладная математика для ВТУЗов, Высшая школа, 2008
23

24. Одномерная оптимизация. Метод квадратичной интерполяции

А. В. Пантелеев, Т. А. Летова Методы оптимизации в примерах и
задачах. Прикладная математика для ВТУЗов, Высшая школа, 2008
24

25. Одномерная оптимизация. Метод квадратичной интерполяции (продолжение)

25

26. Интерполяционный полином Лагранжа

Для заданной таблично функции yi≈f(xi),
i=0..n требуется интерполировать функцию
между узлами интерполяции с
использованием полинома Лагранжа
В. М. Вержбицкий, Основы численных методов, Высшая
школа, 2005 г.
26

27. Линейная задача наименьших квадратов (МНК)

Функция y=f(x) задана таблицей
приближенных значений yi≈f(xi), i=0..n
Для аппроксимации используется
линейная модель:
y= m(x)=a0 0(x)+a1 1(x)+…+am m(x)
Где i(x) – базисные функции,
аi – параметры модели.
Для полиномиальной модели k=xk:
y=Pm(x)=a0+a1x+…+amxm
При m=n многочлен МНК совпадает с
интерполяционным многочленом.
Как правило, при использовании
метода МНК m≤n.
27

28. Метод МНК (продолжение)

В точках xi выполняются приближённые равенства:
Или в матричном
виде: Pa≈y
Из различных критериев выбора
параметров ai наиболее часто используется
критерий наименьших квадратов. Согласно
ему минимизируется среднеквадратичное
отклонение:
28

29. Метод МНК (продолжение)

Опуская промежуточные выкладки,
для получения параметров ai
требуется решить СЛАУ:
Или для случая полиномиальной модели:
А.А. Амосов, Ю.А. Дубинский, Н.В. Копченова, Вычислительные методы
для инженеров, Высшая школа, 1994
29

30. Метод МНК (продолжение)

Для m=1, P1=a0+a1x
Нормальная система имеет вид:
Для m=2, P1=a0+a1x+a2x2
Нормальная система имеет вид:
30

31. Интегрирование. Формулы прямоугольников, трапеций и Симпсона

Квадратурные формулы левых и
правых прямоугольников
Формула трапеций
Формула Симпсона (парабол)
31

32. Квадратурные формулы

Квадратурные формулы:
Хi – узлы;
Аi – веса;
В ранее рассмотренных формулах узлы
равноотстоящие и наборы весов
следующие:
Для формулы трапеций:
h/2, h,...,h, h/2
Для формулы Симпсона:
h/3,4h/3,2h/3,4h/3,...,4h/3,h/3
32

33. Квадратурные формулы (продолжение)

Целесообразно отказаться от
равноотстоящих узлов и преобразовать:
Интеграл преобразуется к виду:
Переходя к квадратурной формуле:
33

34. Квадратурная формула Чебышева

При Аi A = 2/n и таких ti, что формула точна
для многочленов степени n на отрезке [-1;1],
она преобразуется к виду:
Расположение узлов ti вычисляется из решения
системы нелинейных уравнений (здесь не
приводится). Такие наборы ti существуют для
i=1,2,..7,9 и приводятся ниже
34

35. Квадратурная формула Гаусса

При неравенстве Аi друг другу
квадратурная формула имеет более
общий вид.
Узлами её являются корни многочлена
Лежандра, n(t), а веса находятся
интегрированием базисных многочленов
Лежандра.
Общая формула для квадратур Чебышева
и Гаусса на интервале [a,b]
35

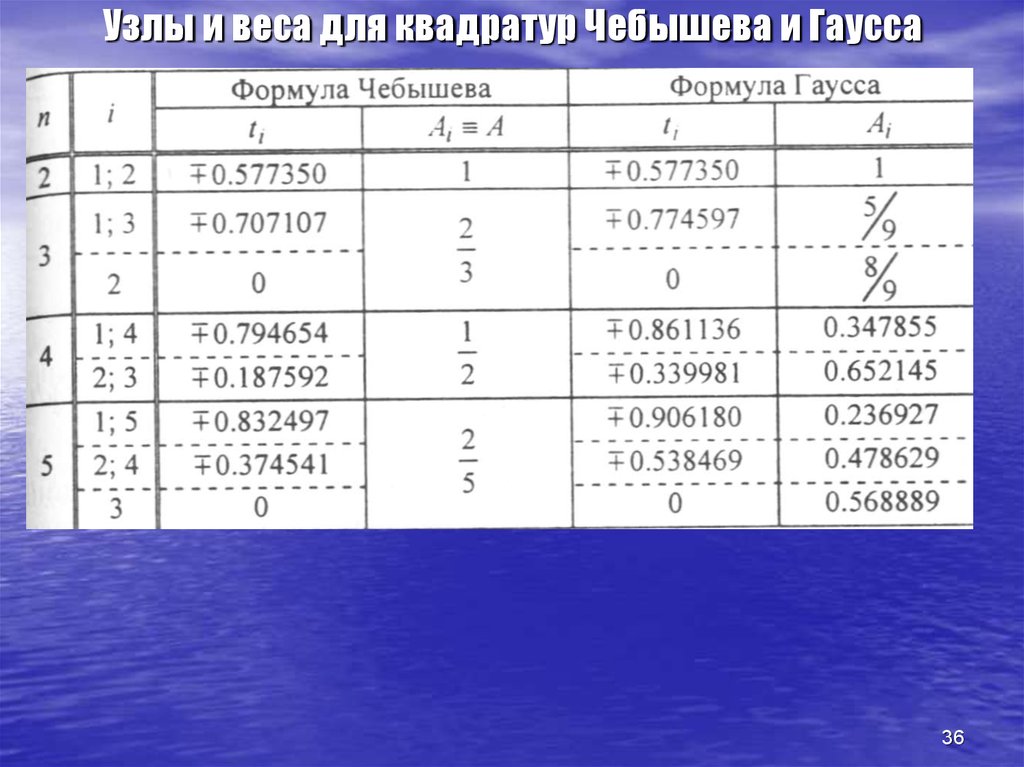
36. Узлы и веса для квадратур Чебышева и Гаусса

36

37. Решение задачи Коши для обыкновенных дифференциальных уравнений

ОДУ 1-го порядка: y’=f(x,y), x [x0,b]
Начальное условие – y(x0)=y0
Метод Эйлера: yi+1=yi+h*f(xi,yi), i=0..n
Метод Эйлера-Коши (Хьюна):
yi+1=yi+h/2*(f(xi,yi)+f(xi+1,yi+hf(xi,yi))),
i=0..n
Метод Рунге-Кутта 4-го порядка:
А.А. Амосов, Ю.А. Дубинский, Н.В. Копченова, Вычислительные методы для37
инженеров, Высшая школа, 1994

38.

38