Similar presentations:
Решение обыкновенных дифференциальных уравнений. Метод Пикара
1.
118.01.2018
2.
Постановка задачиДифференциальные
уравнения
устанавливают связь между независимыми
переменными, искомыми функциями и их
производными. Если искомая функция
зависит от одной переменной, то
дифференциальное уравнение называется
обыкновенным.
3.
Постановка задачиНапример, условие равновесия упругой среды
описывается обыкновенным дифференциальным
уравнением:
dTx
Fx 0
dx
Tx – компонента механических
напряжений, F - действующая на
сплошную среду сила в расчёте на
единицу массы
Здесь искомая функция (механическое
напряжени) T(x) зависит от одной переменной
x (координата).
4. Постановка задачи
В том случае, если искомая функция зависит отнескольких переменных, дифференциальное уравнение
будет уравнением в частных производных.
Например, движение упругой среды можно описать
уравнением в частных производных:
2u x Tx
2
t
x
ux – смещение среды, ρ – плотность
среды, Tx – компонента напряжений
В этом уравнении функция u(t,x) зависит от времени
(t) и направления смещения среды (x).
5.
Постановка задачиОбыкновенными дифференциальными уравнениями
(ОДУ) называются уравнения, которые содержат одну или
несколько производных от искомой функции y = y(x):
F ( x, y, y ,..., y ( n ) ) 0 ,
где x – независимая переменная.
Наивысший порядок n, входящей в уравнение
производной, называется порядком дифференциального
уравнения.
Например:
F ( x, y, y ' ) 0 уравнение первого порядка;
F ( x, y, y ' , y" ) 0 уравнение второго порядка
6.
Постановка задачиИз общей записи дифференциального уравнения
можно выразить производную в явном виде:
y ' f ( x, y ),
y" f ( x, y, y ' )
Уравнение для производных имеет бесконечное
множество решений. Для получения единственного
решения необходимо указать дополнительные
условия, которым должны удовлетворять искомые
решения.
7.
Постановка задачиВ зависимости от вида таких условий
рассматривают три типа задач, для которых доказано
существование и единственность решений.
Первый тип – это задачи с начальными
условиями.
Для
таких
задач
кроме
исходного
дифференциального уравнения в некоторой точке x0
должны быть заданы начальные условия, т.е.
значения функции y (x) и её производных: y (x0) =
y0
y' (x0) = y'0 , . . . , y(n-1) (x0) = yn-10 .
8.
Постановка задачиВторой тип задач – это, так называемые,
граничные, или краевые, в которых
дополнительные условия задаются в виде
функциональных
соотношений
между
искомыми решениями.
Третий тип задач для обыкновенных
дифференциальных уравнений – это задачи на
собственные значения.
9.
Постановка задачиСформулируем задачу Коши.
Найти решение обыкновенного дифференциального
уравнение (ОДУ) первого порядка, разрешенное
относительно производной
y ' f ( x, y ),
удовлетворяющее начальному условию
y ( x0 ) y0
10.
Постановка задачиНеобходимо найти на отрезке [x0,xn] такую
непрерывную функцию
y = y(x), которая
удовлетворяет дифференциальному уравнению
y ' f ( x, y ), и начальному условию y ( x0 ) y0
т.е.
найти
решение
дифференциального
уравнения. Нахождение такого решения называют
решением задачи Коши. Численное решение этой
задачи состоит в построении таблицы приближенных
значений y1,y2,...,yn решения уравнения y(x) в точках
x1,x2,...,xn с некоторым шагом h.
xi x0 i h,
i=1,2,...,n.
11.
Обыкновенныедифференциальные уравнений
Уравнения в частных
производных
z z
dy
0
2( y 3)
2
2
x
y
dx
2
d y
2
2
t
1
2
z
z
dt
3 2 2 4
x
y
3
xdy=y dx
2
y’=x
2
11
2
18.01.2018
12.
Уравнения первого порядкаdy
2( y 3)
dx
Уравнения второго порядка
2
d y
t
1
2
dt
z z
0
2
2
x
y
2
3
xdy=y dx
z z
3 2 2 4
x y
2
2
y′=x
12
2
2
18.01.2018
13.
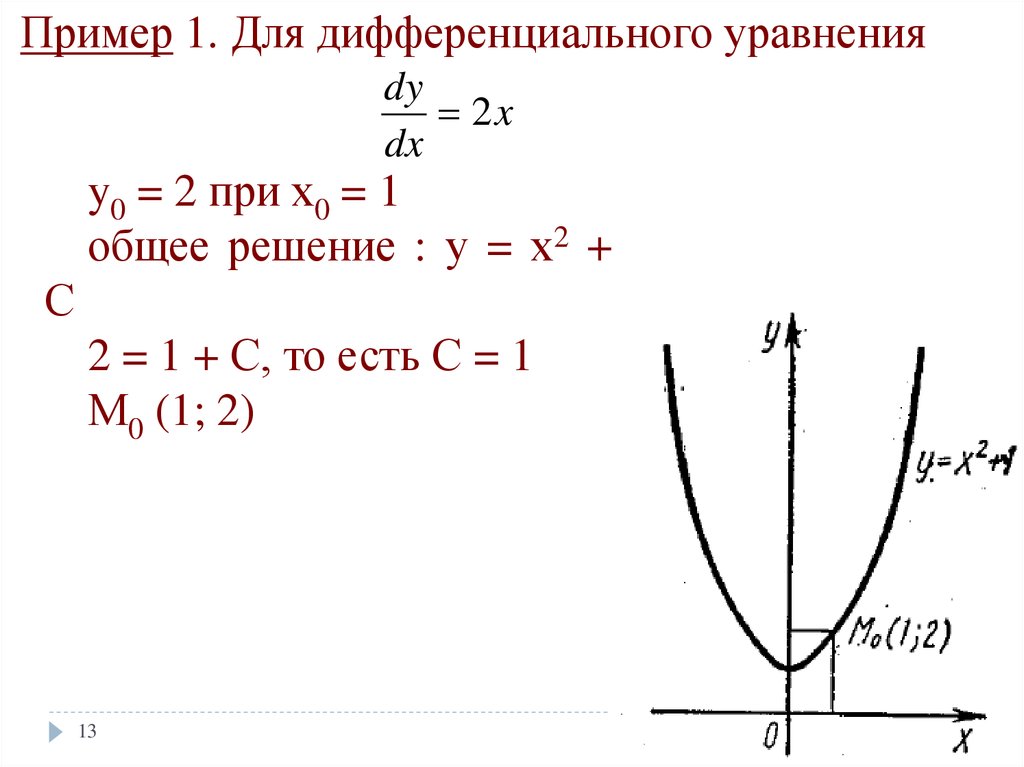
Пример 1. Для дифференциального уравненияdy
2x
dx
y0 = 2 при х0 = 1
общее решение : у = х2 +
С
2 = 1 + С, то есть С = 1
М0 (1; 2)
13
18.01.2018
14.
Условие ЛипшицаR[ a ,b ] {| x x0 | a, | y y0 | b}
f ( x, y) f ( x, y) N y y
14
18.01.2018
15.
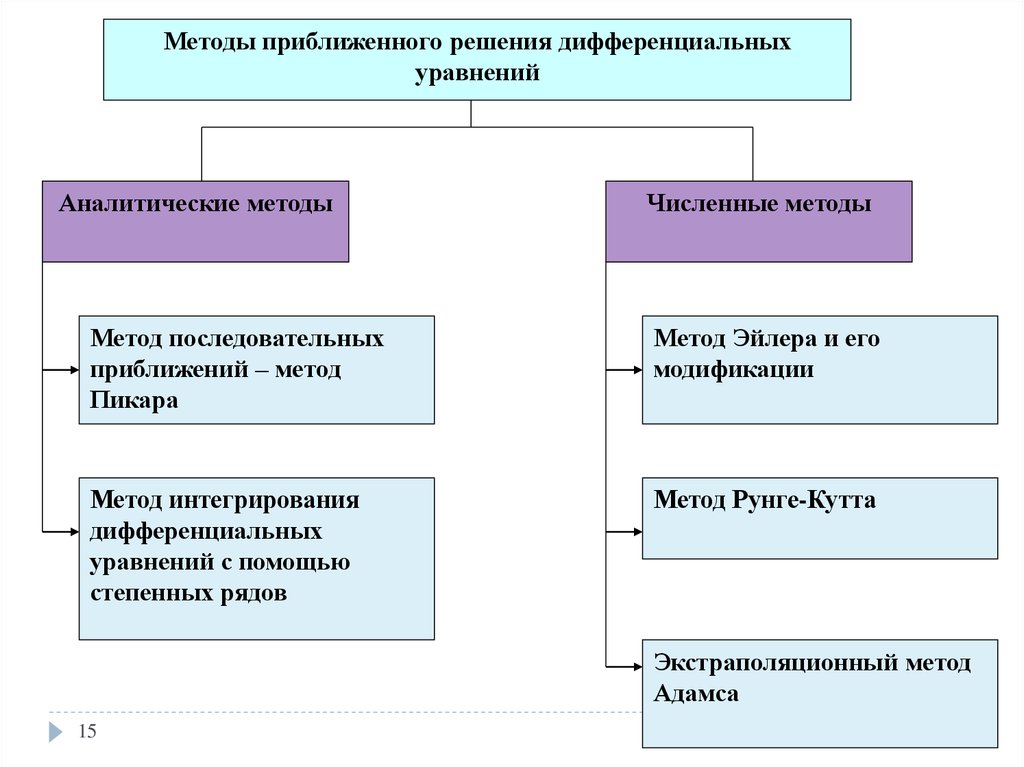
Методы приближенного решения дифференциальныхуравнений
Аналитические методы
Численные методы
Метод последовательных
приближений – метод
Пикара
Метод Эйлера и его
модификации
Метод интегрирования
дифференциальных
уравнений с помощью
степенных рядов
Метод Рунге-Кутта
Экстраполяционный метод
Адамса
15
18.01.2018
16.
18.01.201817.
Решить дифференциальное уравнениеу′=f(x, y) численным методом –
это значит для заданной
последовательности аргументов
х0, х1,…,хn и числа у0,
не определяя функцию у=F(x),
найти такие значения у1, y2, …, yn,
что yi=F(xi) и F(x0)=y0.
h=xk-xk-1
18.01.2018
18.
Пусть дано дифференциальное уравнениепервого порядка
y’= f (x, y)
с начальным условием
x=x0, y(x0)=y0
[a, b]
b a
h
n
шаг интегрирования
18.01.2018
19.
1918.01.2018
20.
xk 1xk 1
f ( x, y) y' dx y( x)
xk
xk 1
xk
y ( xk 1 ) y ( xk ) yk 1 yk
xk
то есть
yk 1 yk
xk 1
f ( x, y )dx
xk
18.01.2018
21.
xk 1f ( x, y)dx f ( x , y ) x
k
k
xk 1
xk
f ( xk , yk )( xk 1 xk ) y ' h
xk
yk 1 yk y'k h
yk 1 yk y'k h
Обозначим
yk 1 yk yk
yk h y'k
yk 1 yk yk
18.01.2018
22.
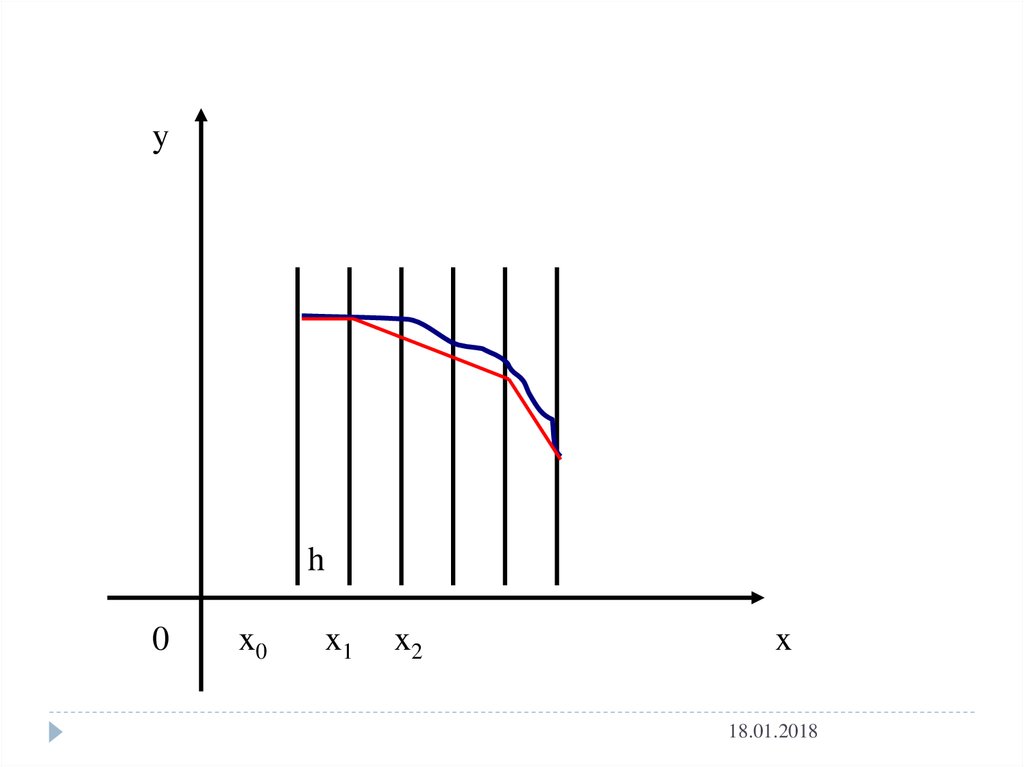
yh
0
x0
x1
x2
x
18.01.2018
23.
Погрешность методаhM
n
y ( xn ) y n
(1 hN ) 1
2N
где
f ( x1 , у1 ) f ( x1 , y2 ) N y1 y2
df
f
f
f
M
dx
x
y
18.01.2018
24.
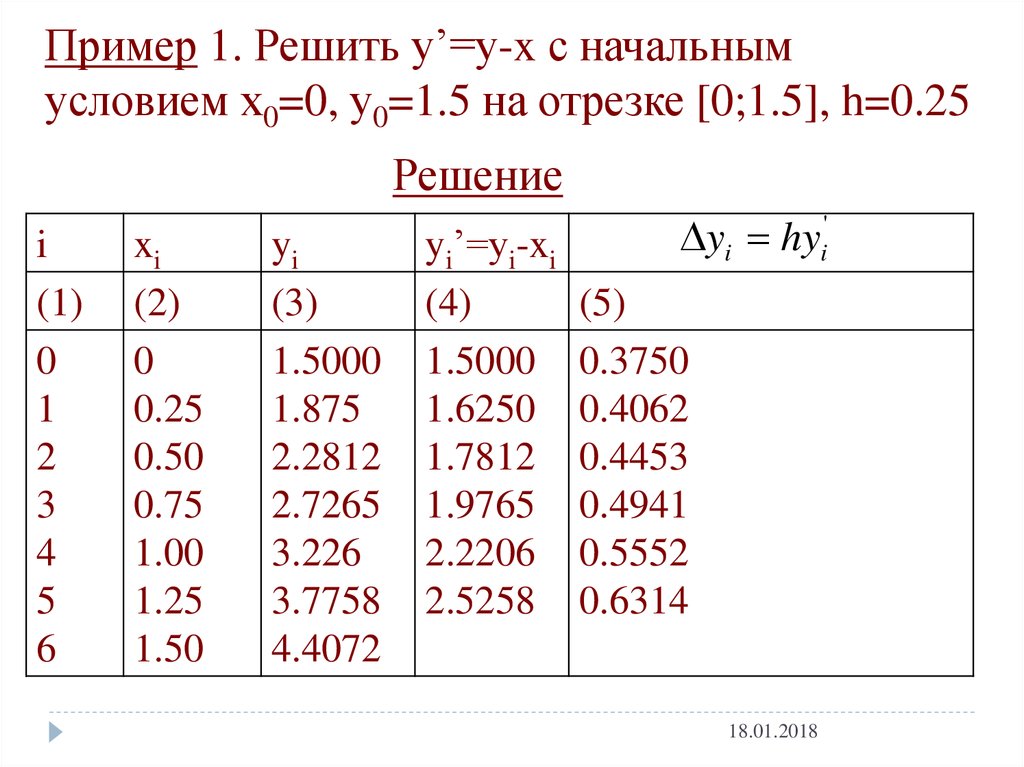
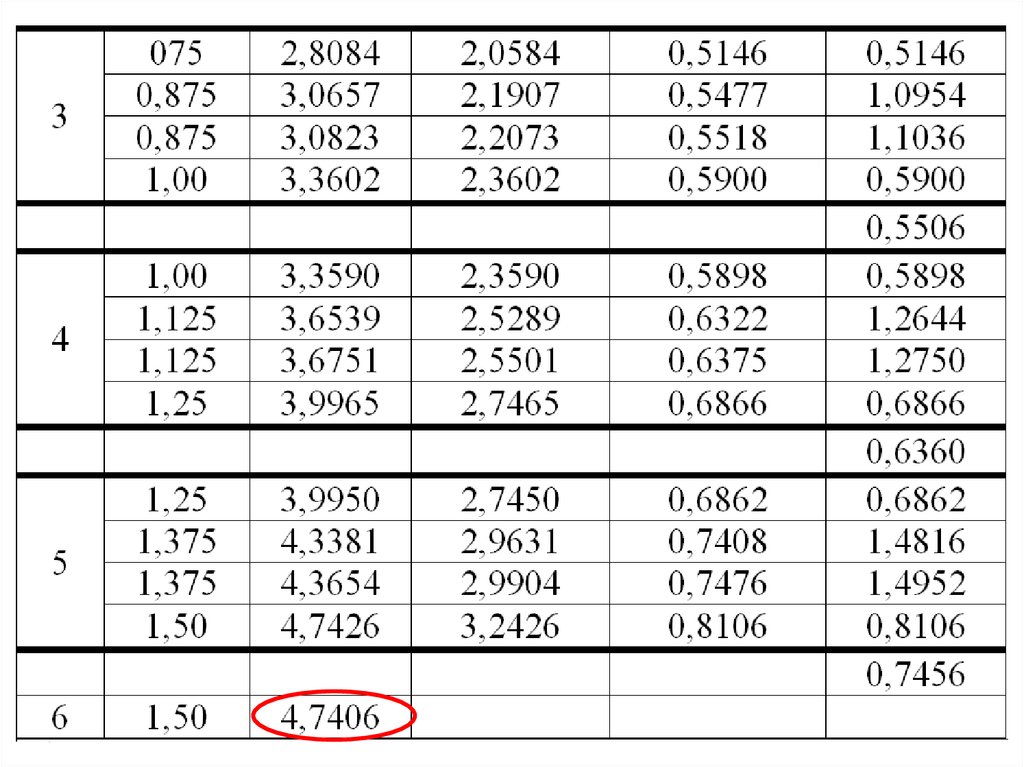
Пример 1. Решить у’=у-x с начальнымусловием х0=0, у0=1.5 на отрезке [0;1.5], h=0.25
Решение
i
(1)
0
1
2
3
4
5
6
xi
(2)
0
0.25
0.50
0.75
1.00
1.25
1.50
yi
(3)
1.5000
1.875
2.2812
2.7265
3.226
3.7758
4.4072
yi’=yi-xi
(4)
1.5000
1.6250
1.7812
1.9765
2.2206
2.5258
yi hy
'
i
(5)
0.3750
0.4062
0.4453
0.4941
0.5552
0.6314
18.01.2018
25.
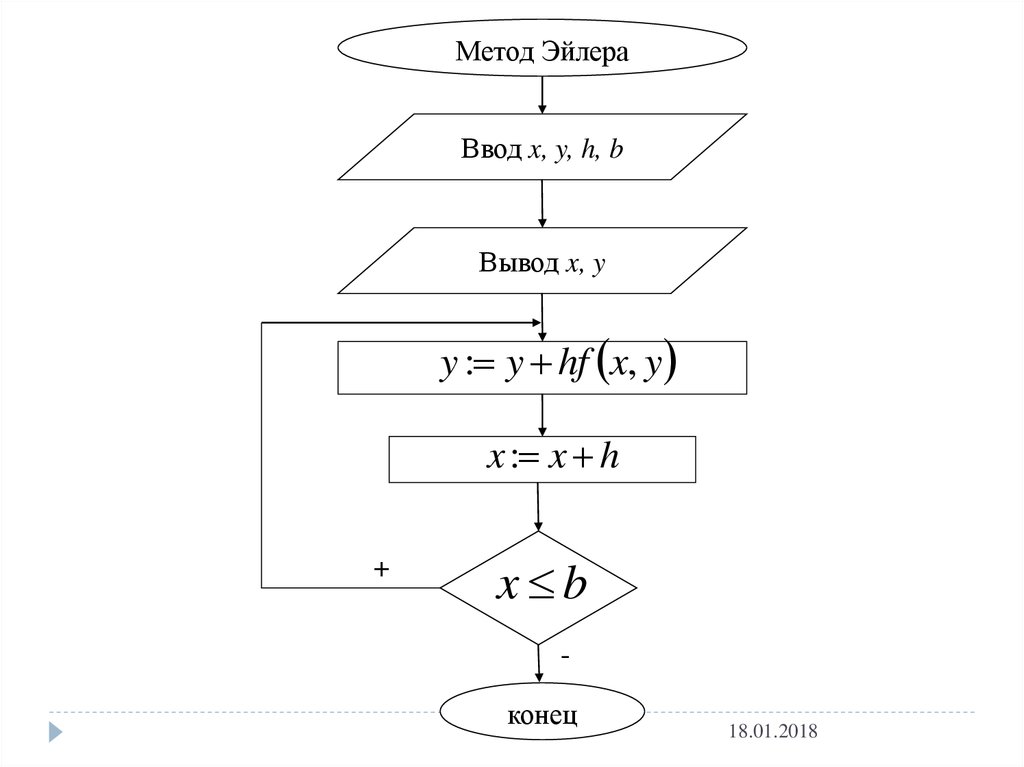
Метод ЭйлераВвод x, y, h, b
Вывод x, y
y : y hf x, y
x : x h
+
x b
конец
18.01.2018
26.
Усовершенствованный метод Эйлераyn+1 = yn + h·[f(tn, yn) + f(tn+1 , y n+1 )]/2
вернемся к разложению функции в ряд Тейлора
повышение точности расчета может быть достигнуто за счет сохранения
члена, содержащего h2. y (t0) можно аппроксимировать конечной разностью:
С учетом этого выражения разложение функции в ряд Тейлора принимает вид
ошибка при этом имеет порядок h3
18.01.2018
27.
18.01.201828.
Задача. Пусть дано дифференциальноеуравнение первого порядка
y’= f(x, y)
с начальным условием
x=x0, y(x0)=y0
Найти решение уравнения на отрезке [a, b]
yi 1 yi yi
18.01.2018
29.
k1 hf ( x, y)h
k1
k 2 hf ( x , y )
2
2
h
k2
k3 hf ( x , y )
2
2
k4 hf ( x h, y k3 )
18.01.2018
30.
1y (k1 2k 2 2k3 k 4 )
6
yi 1 yi yi
18.01.2018
31.
18.01.201832.
Погрешность метода Rn(h5)18.01.2018
33.
Пример 1. Решить дифференциальноеуравнение у′= у-x с начальным
условием х0=0, у(х0)=у0=1.5 методом
Рунге-Кутта. Вычислить с точностью до 0,01.
Решение
k1(0)=(y0-x0)h=1.5000*0.25=0.3750
k 2( 0)
k1( 0)
h
x0 h (1.5000 0.1875) 0.125 0.25 0.3906
y0
2
2
18.01.2018
34.
k3( 0)k 2( 0)
h
x0 h (1.5000 0.1953) 0.125 0.25 0.3926
y0
2
2
k4(0)=[(y0+k3(0))-(x0+h)]h=[(1.5000+0.3926)0.125]*0.25=0.4106
1
y0 (0.3750 2 * 0.3906 2 * 0.3926 0.4106)
6
=0,3920
y1=1.50000+0.3920=1.8920
18.01.2018
35.
18.01.201836.
18.01.201837.
Метод Рунге-Кутта при решении системдифференциальных уравнений
,
y ' f ( x, y , z )
z
'
g
(
x
,
y
,
z
)
18.01.2018
38.
1 (i )(i )
(i )
(i )
yi (k1 2k 2 2k3 k 4 )
6
1 (i )
(i )
(i )
(i )
zi (l1 2l2 2l3 l4 )
6
, где
18.01.2018
39.
(i )1
k
(i )
1
l
hf ( xi , yi , zi )
hq( xi , yi , zi )
18.01.2018
40.
kl
(i )
2
(i )
2
(i )
1
(i )
1
h
k
l
hf ( xi , yi
, zi )
2
2
2
(i )
1
(i )
1
h
k
l
hq( xi , yi
, zi )
2
2
2
18.01.2018
41.
k(i )
3
(i )
3
l
(i )
2
(i )
2
(i )
2
(i )
2
h
k
l
hf ( xi , yi
, zi )
2
2
2
h
k
l
hq( xi , yi
, zi )
2
2
2
18.01.2018
42.
kl
,
(i )
4
(i )
4
(i )
3
k
h
(i )
hf ( xi , yi
, zi l3 )
2
2
(i )
3
k
h
(i )
hq( xi , yi
, z i l3 )
2
2
yi 1 yi yi
zi 1 zi zi
18.01.2018
43.
Метод последовательных приближений43
18.01.2018
44.
Первое приближение:Второе приближение:
Третье приближение:
…
n-е приближение:
44
18.01.2018
45.
Теорема. Пусть в окрестности точки (х0; у0)функция f(х, у) непрерывна и имеет
ограниченную частную производную f’y (х, у).
Тогда в некотором интервале, содержащем
точку х0, последовательность { yi(x)}
сходится к функции у(х), служащей
решением дифференциального
уравнения у’ = f(х, у) и
удовлетворяющей условию у (х0) = у0
45
18.01.2018
46.
Оценка погрешности метода Пикараn 1
h
| y yn | N M
(n 1)!
n
где М = mах |f(х, у)|
N = mах |f ’y(х, у)|
b
h min a,
M
46
18.01.2018
47. Метод Пикара последовательных приближений
Дифференциальное уравнение n-ого порядкаРассмотрим дифференциальное уравнение первого
порядка
y’ = f(x, y)
(1)
с начальными условиями
y(x0) = y0
(2).
Предполагается, что в некоторой окрестности точки
M0(x0, y0) уравнение (1) удовлетворяет условиям теоремы
существования и единственности решения.
48.
Будем строить искомое решение y = y(x) для значенийx x0 .
Случай x x0 аналогичен.
Интегрируя правую и левую части уравнения (1) в
пределах от x0 до x, получим
x
y ( x) y ( x0 ) f ( x, y )dx
x0
или в силу начального условия (2), будем иметь
x
y ( x) y0 f ( x, y )dx
x0
(3)
49.
Так как искомая функция y = y(x) находится подзнаком интеграла, то уравнение (3) является
интегральным.
Очевидно, решение интегрального уравнения (3)
удовлетворяет дифференциальному уравнению (1) и
начальному условию (2).
Для нахождения этого решения применим метод
последовательных приближений.
Заменяя в равенстве (3) неизвестную функцию y
данным значением y0, получим первое приближение
x
y1 y0 f ( x, y0 )dx
x0
50.
Далее подставив в равенстве (3) вместо неизвестнойфункции y найденную функцию y1, будем иметь второе
приближение
x
y2 y0 f ( x, y1 )dx
и т.д.
x0
Все дальнейшие приближения строятся по формуле
x
yn y0 f ( x, yn 1 )dx
(n = 1, 2, …)
x0
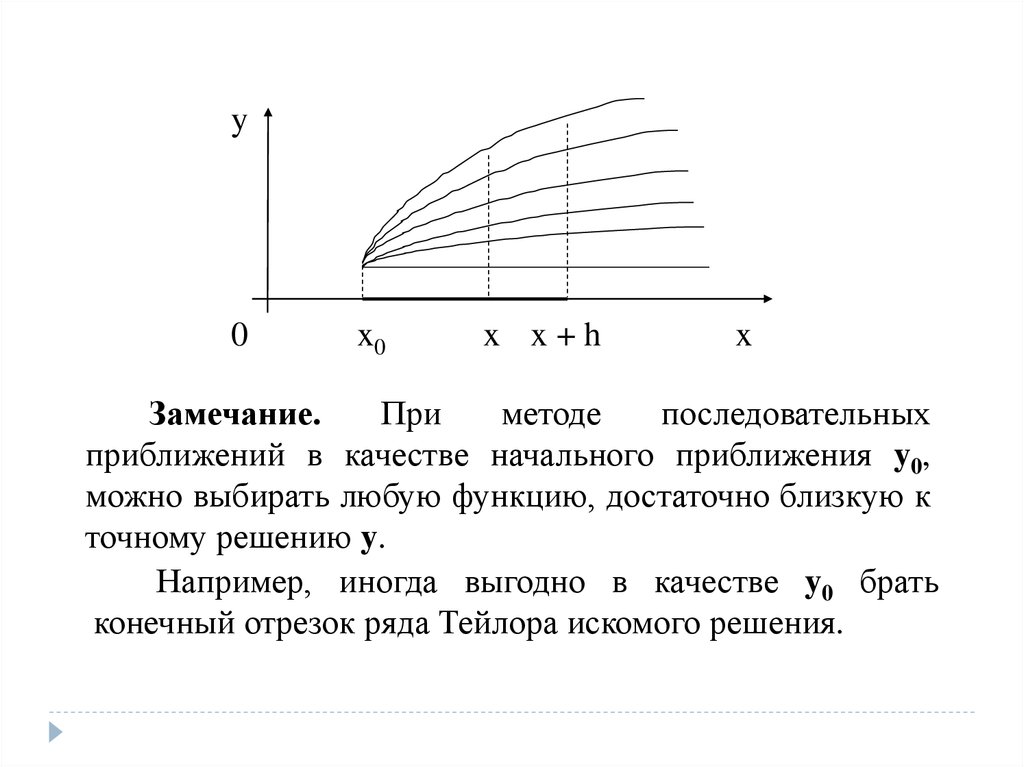
Геометрически
последовательные
приближения
представляют собой кривые yn = yn(x) (n = 1, 2, …),
проходящие через общую точку M0(x0, y0).
51.
y0
x0
x x+h
x
Замечание.
При
методе
последовательных
приближений в качестве начального приближения y0,
можно выбирать любую функцию, достаточно близкую к
точному решению y.
Например, иногда выгодно в качестве y0 брать
конечный отрезок ряда Тейлора искомого решения.
52.
Заметим,что
при
пользовании
методом
последовательных приближений аналитичность правой
части дифференциального уравнения необязательна,
поэтому этот метод можно применять и в тех случаях,
когда
разложение
решения
дифференциального
уравнения в степенной ряд невозможно.
Пример 1. Методом последовательных приближений
найти приближенное решение дифференциального
уравнения
y’ = x – y,
Удовлетворяющее начальному условию y(0) = 1.
53.
Решение. В качествевозьмем y0(x) = 1. Так как
начального
приближения
x
y 1 ( x y)dx
0
то будем иметь
x
x2
y1 1 ( x 1)dx 1 x
2
0
Аналогично
3
x2
x
dx 1 x x 2
y2 1 x 1 x
2
6
0
x
54.
Подобным же образом получим3
4
x
x
y3 1 x x 2
3 24
3
4
5
x
x
x
y4 1 x x 2
3 12 120
и т.д.
55. Система дифференциальных уравнений (метод Пикара)
Дана система дифференциальных уравненийdy
f ( x, y )
dx
(4)
y( x0 ) y0
(5)
где
Записывая векторное уравнение (4) в интегральной
форме, будем иметь
56.
xy y0 f ( x, y )dx
(6)
x0
где под интегралом от вектор-функции
понимается вектор
x
x0
x
f1 dx
x0
f dx
x
f n dx
x0
f1
f
f n
57.
Последовательные приближенияопределяются по формуле
x
y
( p)
y 0 f ( x, y
( p 1)
y ( p ) (p = 1, 2, …)
)dx
x0
Причем обычно полагают
y (0) y
Этот метод годится также для дифференциального
уравнения n-го порядка, если его записать в виде
системы.
58.
Пример 2. Построить несколько последовательныхприближений для решения системы
dy1
dx x y1 y2
dy2 x 2 y 2
1
dx
удовлетворяющего начальным условиям
y1(0) = 1; y2(0) = 0
59.
Решение. Имеем:x
y1 1 ( x y1 y2 )dx
0
x
y2 ( x2 y12 )dx
0
Отсюда, полагая
y1(0) = 1;
y2(0) = 0
получаем
x
2
x
(1)
y1 1 ( x 0)dx 1
2
0
x
3
x
(1)
y2 ( x 2 1)dx x
3
0
60.
x 2x 3
x 4 x6
1 x 1 x dx 1
2
3
24 36
0
x
(2)
1
y
4
5
2
x
x
x 1 x 2 dx x
4
20
0
x
y2
(2)
и т.д.
61.
Окончание вычисленийn 1
h
| y yn | N M
(n 1)!
n
61
18.01.2018
















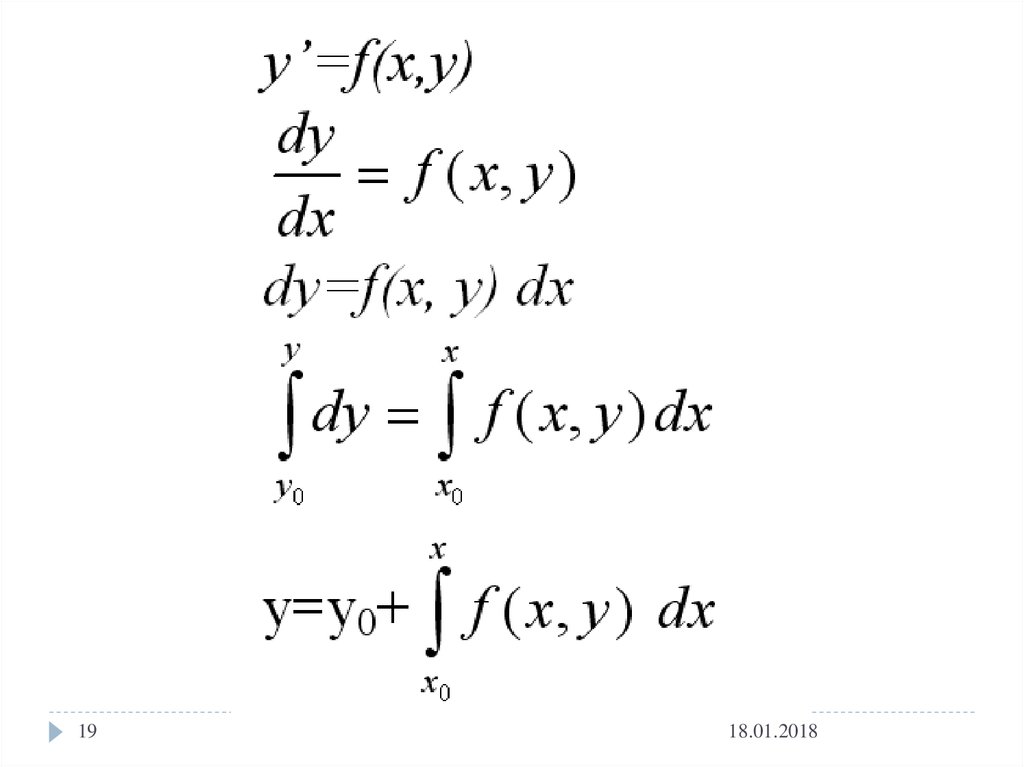
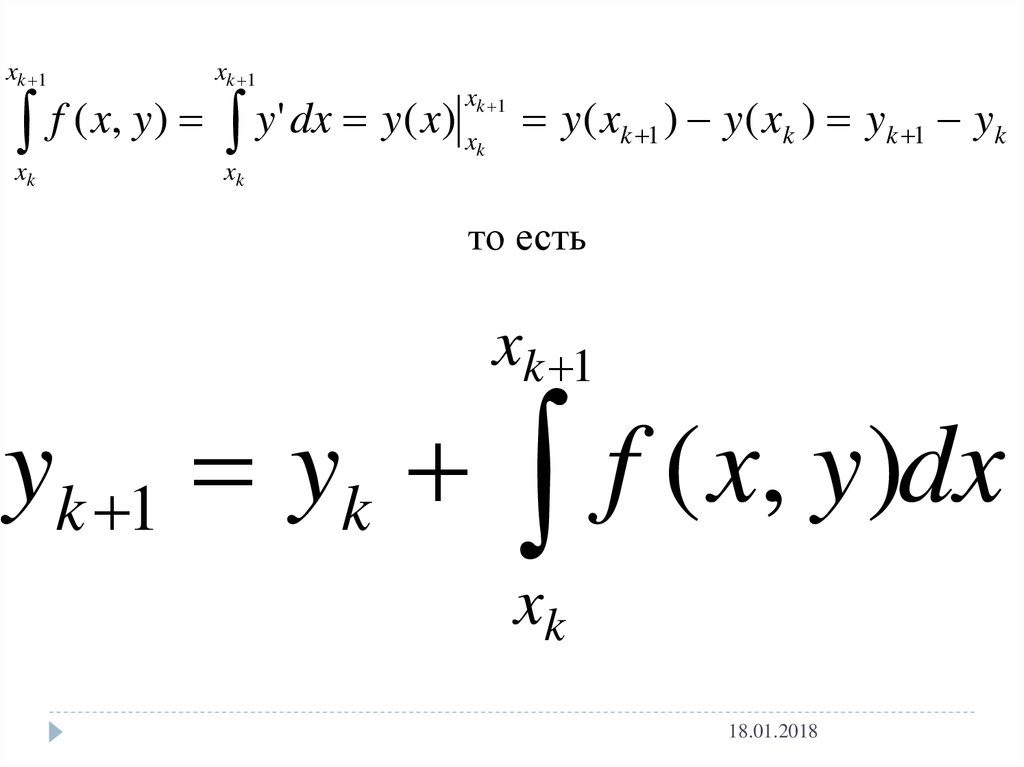





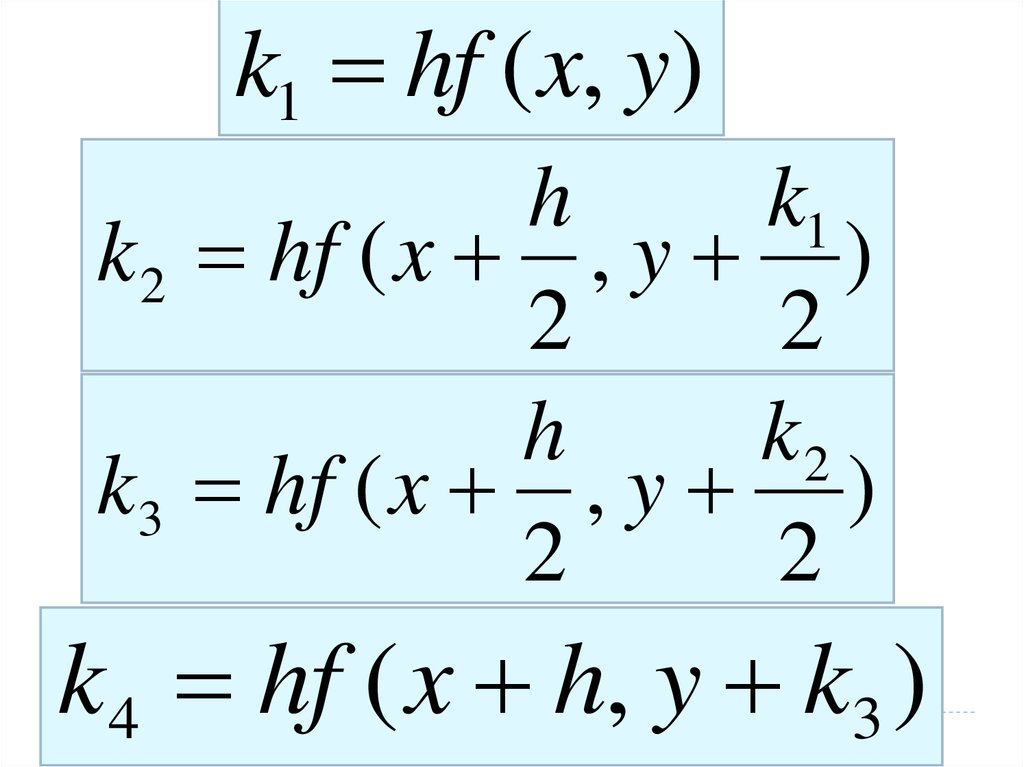
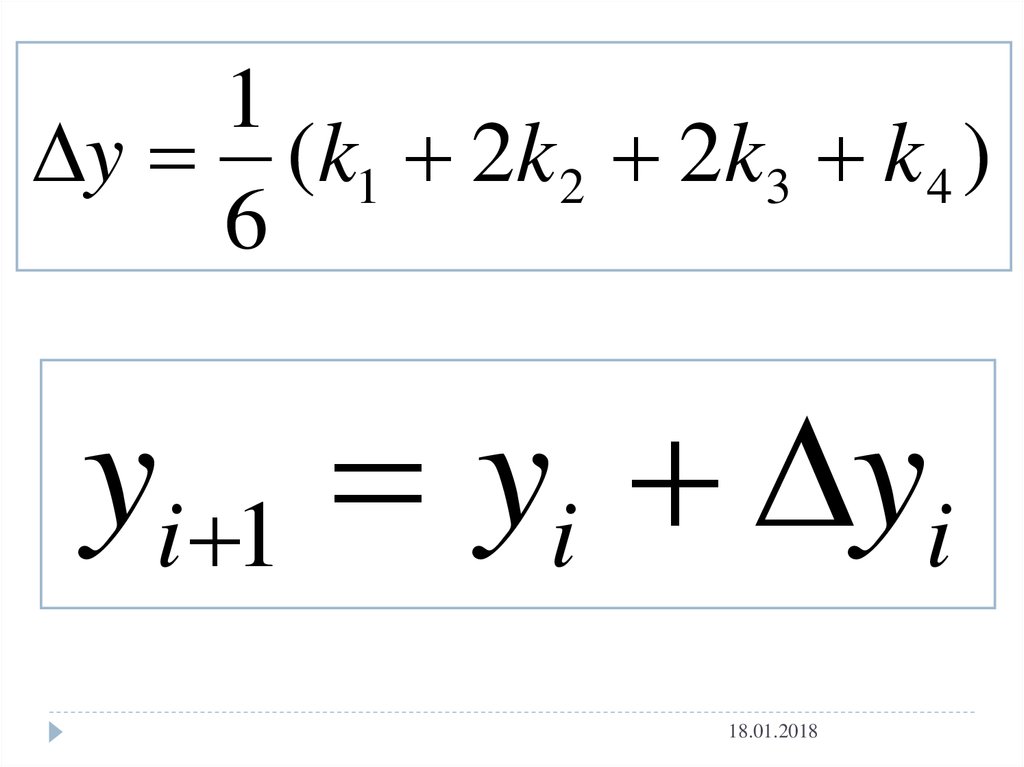






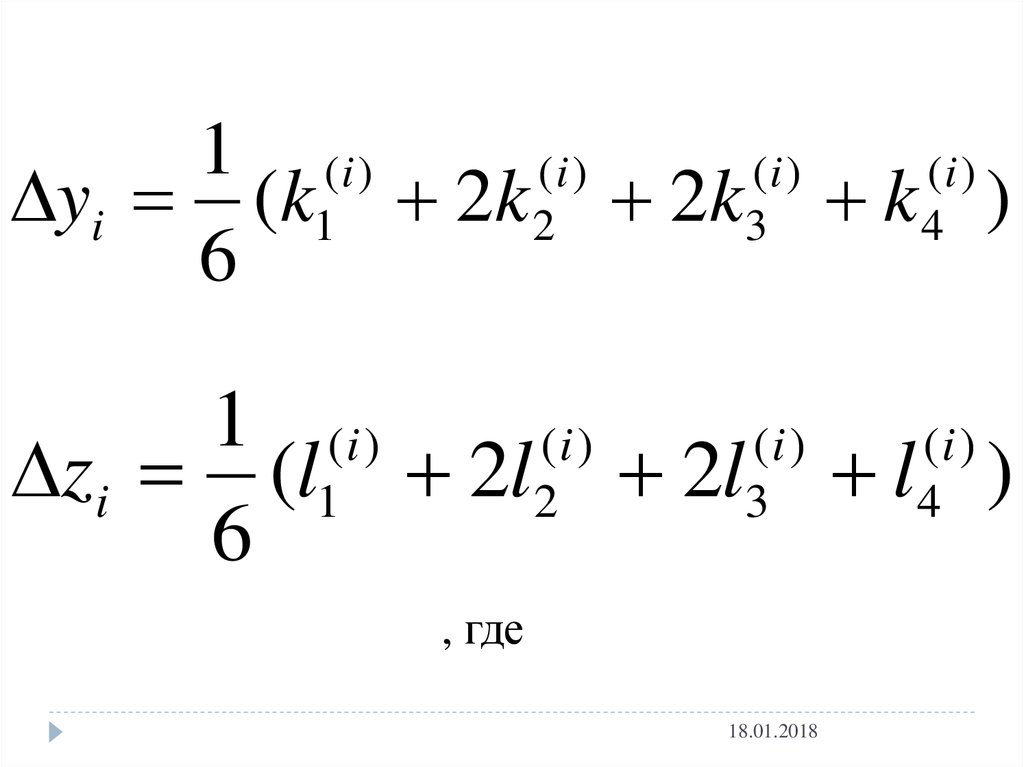
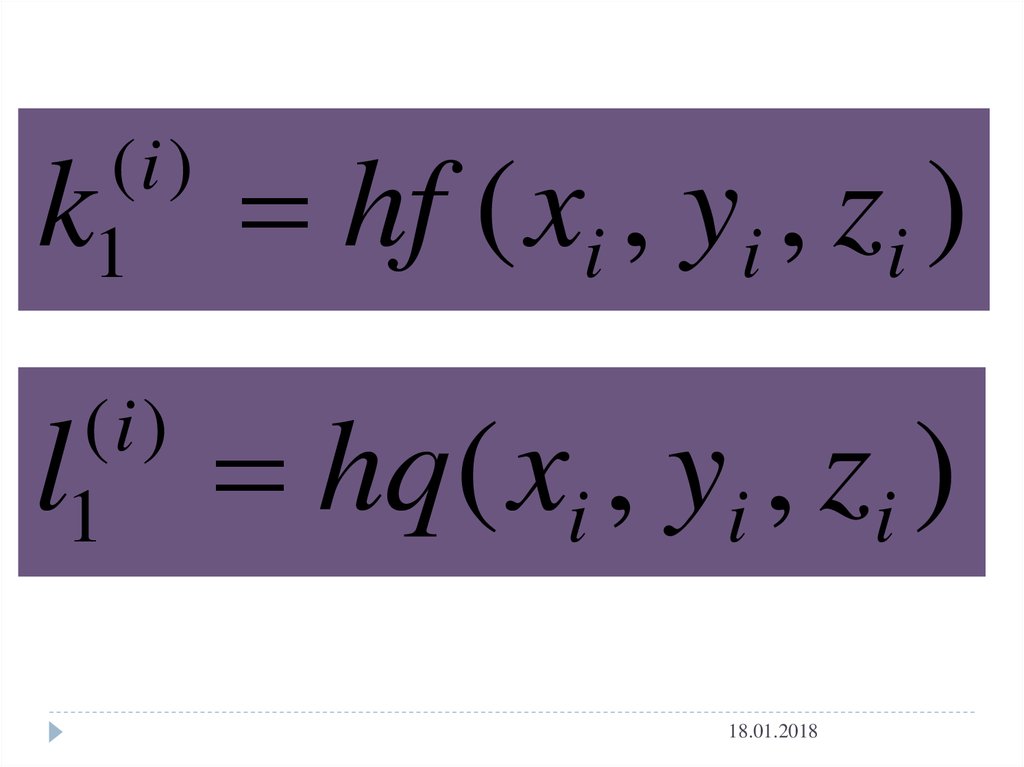





















 mathematics
mathematics








